등측 부등식

수학에서 이등분포는 집합의 둘레와 그 부피를 포함하는 기하학적 불평등이다. In ${\displaystyle n}$-dimensional space ${\displaystyle \mathbb {R} ^{n}}$ the inequality lower bounds the surface area or perimeter ${\displaystyle \operatorname {per} (S)}$ of a set ${\displaystyle S\subset \mathbb {R} ^{n}}$ by its volume ${\displaystyle \operatorna$$me {vol} (S$

${\displaystyle \operatorname {per} (S)\geq n\operatorname {vol} (S)^{\frac {n-1}{n}}\,\operatorname {vol} (B_{1})^{\frac {1}{n}}}$,

여기서 $B{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$^{$n}}$은 단위 구이다. 동등성은 $S{\displaystyle }$ ${\displaystyle S}$이(가) $R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$의 구체일$$ 때만 유지된다$.$

평면에서, ${\displaystyle \mathrm{예}}$를 들어${\displaystyle ,}$ n =$$2 {\$displaystyle n=2$}일 때$,$ 등측 불평등은 닫힌 곡선의 원주 원주의 제곱과 그것이 둘러싸고 있는 평면 영역의 면적에 관련된다. Isoperimetric은 문자 그대로 "같은 둘레를 가지고 있다"는 뜻이다. 특히 $R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\$에서$$등측 불평등은 닫힌 곡선의 길이 L과 이 곡선이 감싸는 평면 영역의 A 영역에 대해 다음과 같이 명시한다.

${\displaystyle L^{2}\geq 4\pi A,}$

그리고 그 평등은 곡선이 원일 경우에만 유지된다.

등측위 문제는 경계가 지정된 길이를 갖는 가능한 가장 큰 면적의 평면 수치를 결정하는 것이다.^[1] 밀접하게 연관된 디도의 문제는 직선으로 경계된 최대 영역과 끝점이 그 선에 속하는 곡선 형태의 영역을 요구한다. 카르타고의 전설적인 창시자이자 최초의 여왕인 디도의 이름을 따서 지어졌다. 이등변수 문제에 대한 해결책은 원에 의해 주어지며 고대 그리스에서는 이미 알려져 있었다. 그러나 이 사실에 대한 최초의 수학적으로 엄격한 증거는 19세기에야 얻어졌다. 그 이후로 많은 다른 증거들이 발견되었다.

등측위 문제는 예를 들어 표면의 곡선과 고차원 공간의 영역으로 확장되었다. 아마도 3차원 등측불평등의 가장 친숙한 물리적 징후는 물방울 모양일 것이다. 즉, 방울은 일반적으로 대칭 원형을 가정한다. 한 방울의 물의 양이 고정되어 있기 때문에, 표면 장력은 그 방울의 표면적, 즉 둥근 구를 최소화하는 모양으로 떨어지게 한다.

평면의 등거리계 문제

고전적인 등거리 문제는 옛날로 거슬러 올라간다.^[2] 이 문제는 다음과 같이 진술할 수 있다. 고정된 둘레 평면의 모든 닫힌 곡선 중에서 어떤 곡선(있는 경우)이 밀폐된 영역의 면적을 최대화하는가? 이 질문은 다음과 같은 문제와 동등하다고 보여질 수 있다. 고정 영역을 둘러싸는 평면의 모든 닫힌 곡선 중에서 둘레를 최소화하는 곡선(있는 경우)은?

이 문제는 물리학의 최소 행동 원칙과 개념적으로 관련이 있는데, 그것은 다시 정리될 수 있다는 것이다: 가장 큰 영역과 가장 큰 노력의 경제성을 가진 가장 큰 영역을 둘러싸는 행동 원리는 무엇인가? 15세기 철학자 겸 과학자인 쿠사의 니콜라스 추기경은 원이 생성되는 과정인 회전 작용을 감각적 인상의 영역, 우주가 생성되는 과정의 가장 직접적인 반영이라고 생각했다. 독일의 천문학자 겸 점성가 요하네스 케플러는 미스테리움 코스모그래픽(The Sacred Mystery of the Cosmos, 1596년)에서 태양계의 형태론을 논하면서 등측 원리를 발동시켰다.

비록 원이 문제의 명백한 해결책으로 보이지만, 이 사실을 증명하는 것은 다소 어렵다. 해법으로 향한 첫 진전은 1838년 스위스의 지오미터 야콥 슈타이너에 의해 이루어졌는데, 후에 슈타이너 대칭이라는 기하학적 방법을 사용하였다.^[3] 슈타이너는 만약 해결책이 존재한다면, 그때는 반드시 원이 되어야 한다는 것을 보여주었다. 슈타이너의 증거는 나중에 몇몇 다른 수학자들에 의해 완성되었다.

Steiner는 쉽게 이해할 수 있는 몇몇 기하학적 구조로 시작한다. 예를 들어, 완전히 볼록하지 않은 영역을 둘러싸는 닫힌 곡선은 오목한 영역이 볼록해지도록 "플립"함으로써 더 많은 영역을 둘러싸도록 수정할 수 있다는 것을 보여줄 수 있다. 또한 완전히 대칭되지 않은 닫힌 곡선은 더 많은 면적을 둘러싸도록 "경사"될 수 있음을 보여줄 수 있다. 완벽하게 볼록하고 대칭적인 한 가지 모양은 원이지만, 이것 자체가 이등변수 정리(외부 연결 참조)의 엄격한 증거를 나타내지는 않는다.

비행기에서

이등변수 문제에 대한 해결책은 일반적으로 닫힌 곡선의 길이 L과 그것이 에워싸는 평면 영역의 영역 A와 관련된 불평등의 형태로 표현된다. 등측불평등은 다음과 같이 말하고 있다.

${\displaystyle 4\pi A\leq L^{2},}$

그리고 곡선이 원일 경우에만 평등이 유지된다. 반지름 R의 원반 면적이 rR이고² 원의 둘레가 2rR이므로 이 경우 불평등의 양쪽이 모두 4πR과²² 같다.

이등분포 불평등에 대한 수십 가지 증거가 발견되었다. 1902년, 후르비츠는 임의의 수정 가능한 곡선(평활하다고 가정하지 않음)에 적용되는 푸리에 시리즈를 이용한 짧은 증거를 발표했다. 매끄러운 단순 닫힌 곡선과 적절한 원을 비교한 우아한 직접 증명이 E에 의해 주어졌다. 1938년 슈미트 호 길이 공식, 그린의 정리로부터 평면 영역의 면적에 대한 표현, 카우치-슈워즈 불평등만을 사용한다.

주어진 닫힌 곡선의 경우, 등비율은 그 면적과 동일한 둘레를 가진 원의 비율로 정의된다. 이것은 와 같다.

${\displaystyle Q={\frac {4\pi A}{L^{2}}$

그리고 등비평등은 Q ≤ 1. 동등하게 등비평가는 곡선마다² 최소 4 π이다.

일반 n곤의 등비계수 지수는 다음과 같다.

${\displaystyle Q_{n}={\frac {\pi }{n\tan {\tfrac {\pi }}}.}$

$C{\displaystyle }$ ${\displaystyle C}$을(를) 부드러운 일반 볼록형 닫힘 곡선이 되도록$$ 한다. 그 후 개선된 등측불평등은 다음과 같이 말한다.

${\displaystyle L^{2}\geqslant 4\pi A+8\pi \왼쪽 {\widetilde{A}_{0.5}\오른쪽, }$

where ${\displaystyle L,A,{\widetilde {A}}_{0.5}}$ denote the length of ${\displaystyle C}$, the area of the region bounded by ${\displaystyle C}$ and the oriented area of the Wigner caustic of ${\displaystyle C}$, respectively, and the equality holds if and only if ${\displaystyle C}$ 일정한 폭의 곡선이다.^[4]

구 위에

C는 반지름 1의 구에 있는 단순 폐쇄 곡선이다. L로 C의 길이를 표시하고 A로 C로 둘러싸인 영역을 표시한다. 구면 등측불평등은 다음과 같이 말하고 있다.

${\displaystyle L^{2}\geq A(4\pi -A),}$

그리고 곡선이 원일 경우에만 평등이 유지된다. 사실 단순한 닫힌 곡선으로 둘러싸인 구면적을 측정하는 방법에는 두 가지가 있지만, 그 불평등은 보완을 취하는 것과 관련하여 대칭적이다.

이 불평등은 폴 레비(1919년)에 의해 발견되었는데, 그는 또한 이것을 더 높은 치수와 일반 표면으로 확장시켰다.^[5]

보다 일반적인 임의 반지름 R의 경우는 다음과 같이 알려져 있다.

${\displaystyle L^{2}\geq 4\pi A-{{\frac {A^{2}}:{R^{2}}.}$

$R{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$의 경우

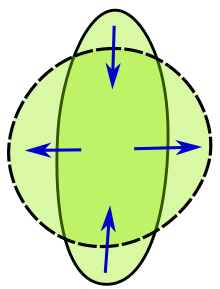
등측 불평등은 구가 주어진 부피당 표면적이 가장 작다고 말한다. 경계 ${\displaystyle {\mathbb{}}^{}}$ $S{\displaystyle }$ ${\displaystyle \subset }$ ${\displaystyle {}^{}}$$$ ${\$에 }} ($displaystyle \operatorname {per}(S)$ 및 ${\displaystyle \mathrm{볼륨<img\; alt="\{\backslash displaystyle\; \backslash operatorname\; \{per\}\; (S)\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/7b01e2249950cfa6e8e2553fda81364592d307f3"\; style="vertical-align:\; -0.838ex;\; width:6.545ex;\; height:2.843ex;">}}$ ${\displaystyle \{}$(${\displaystyle S}$) ${\displaysty \operatorname {vol}(S)$이)이(으)인 경우$$$,$ 등측 불평등 상태가 된다.

${\displaystyle \operatorname {per} (S)\geq n\operatorname {vol} (S)^{\frac {n-1}{n}}\,\operatorname {vol} (B_{1})^{\frac {1}{n}}}$,

여기서 $B{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$^{$n}}$은 단위공이다. 동등성은 $S{\displaystyle }$ ${\displaystyle S}$이(가) ${\displaystyle {}^{}}$ ${\$^{$n}$의 공일$$ 때 유지된다$.$ 집합에 대한 추가 제한(볼록도, 규칙성, 매끄러운 경계 등)에 따라 동등성은 공에 대해서만 유지된다. 그러나 전반적으로 상황은 더 복잡하다. 슈미트(1949, 20.7장)의 관련 결과(1957년, 5.2.5장)는 다음과 같이 하드와이거(1957년, 5.2.5장)에서 명확히 한다. 극세트는 공과 "코로나"로 구성되어 볼륨이나 표면적에 기여하지 않는다. That is, the equality holds for a compact set ${\displaystyle S}$ if and only if ${\displaystyle S}$ contains a closed ball ${\displaystyle B}$ such that ${\displaystyle \operatorname {vol} (B)=\operatorname {vol} (S)}$ and ${\displaystyle \operatorname {per}$$(B)=\operatorname {per}(S).}$예를$$ 들어 "코로나"는 곡선일 수 있다.

The proof of the inequality follows directly from Brunn–Minkowski inequality between a set ${\displaystyle S}$ and a ball with radius ${\displaystyle \epsilon }$, i.e. ${\displaystyle B_{\epsilon }=\epsilon B_{1}}$. By taking Brunn–Minkowski inequality to the power ${\displaystyle n}$, subtracting $$${\displaystyle \mathrm{볼륨}}$vol${\displaystyle }$(${\displaystyle S}$) ${\displaystyle \operatorname {vol} (S)}$ 양쪽에서$$ $ϵ{\displaystyle }$ ${\displaystyle \epsilon$ $\}$로 나누고, 한도를 $ϵ{\displaystyle }$→ ${\displaystyle 0.}$ ${\displaysty \epsilon \to.}($Osserman(1978), 페더러(1969, 제3.2.43)로 한다.

완전한 일반성(Federerer 1969, 제3.2.43)에서, 등측 불평등은 닫힘이 유한한 Lbesgue 측정을 가진 모든$$ 집합 $S{\displaystyle }$ ${\displaystyle \subset }$ ${\displaystyle {}^{}}$ ${\$에 대해 명시한다.

${\displaystyle n\,\omega _{n}^{n1}{n}{n}{n1}({\bar{S})^{n-1}{n}\leq M_{*}^{n-1}(\partial S)}}$

where ${\displaystyle M_{*}^{n-1}}$ is the (n-1)-dimensional Minkowski content, Lⁿ is the n-dimensional Lebesgue measure, and ω_n is the volume of the unit ball in ${\displaystyle \mathbb {R} ^{n}}$. If the boundary of S is rectifiable, then the Minkowski content is the (n-1)-dimensional Hausdorff measure.

n-차원 등차계 불평등은 (충분히 부드러운 영역에 대해) R ${\displaystyle {}^{}}$ ${\$의 Sobollev 불평등과 동등하며, 최적의$$ 상수는 다음과 같다.

${\displaystyle \left(\int _{\mathbb {R} ^{n}} u ^{\frac {n}{n-1}}\right)^{\frac {n-1}{n}}\leq n^{-1}\omega _{n}^{-{\frac {1}{n}}}\int _{\mathbb {R} ^{n}} \nabla u }$

모든 $u{\displaystyle }$ ${\displaystyle \in }$ ${\displaystyle {}^{}}$ ${\displaystyle {1\mathrm{}}^{}}$,${\displaystyle {}^{}}$1${\displaystyle {}^{}}$( ${\displaystyle {}^{}}$ n${\displaystyle {}^{}}$) ${\displaystyle u\in W^1,1}(\mathb {R} ^{n})$에 대해 $.$

하다마드 다지관

Hadamard 다지관은 비양성 곡률로 단순하게 연결된 다지관이다. 따라서 그들은 곡률 0의 Hadamard 다지관인 유클리드 $공간{\displaystyle {\mathbb{}}^{}}$ ${\displaystyle {}^{}}$ ${\$을 일반화한다. 1970년대와 80년대 초반, 티에리 오빈, 미샤 그로모프, 유리 부라고, 빅토르 잘갈레르 등은 유클리드인의 등극 불평등을 추측했다.

${\displaystyle \operatorname {per}(S)\geq n\operatorname {vol}(S)^{\frac {n1}{n1}:{n}}}\operatorname {vol}(B_{1})^{\frac {1}{n}}}}}}}$

Cartan-Hadamard 추측으로 알려진 Hadamard 다지관의 경계$$ 세트 $S{\displaystyle }$ ${\displaystyle S}$에 대한 홀드. 차원 2에서 이것은 1926년에 당시 하다마르의 학생이었던 안드레 웨일에 의해 이미 확립되었다. 치수 3과 4에서는 1992년 브루스 클라이너, 1984년 크리스 크로케에 의해 각각 추측이 증명되었다.

미터법 측정 공간

이등분계 문제에 대한 대부분의 작업은 유클리드 공간의 평탄한 지역, 또는 더 일반적으로 리만 다지관의 맥락에서 이루어졌다. 그러나 이등분계 문제는 민코프스키 콘텐츠의 개념을 이용하여 훨씬 더 큰 일반성으로 공식화될 수 있다. Let${\displaystyle }$( ${\displaystyle X}$, ${\displaystyle \mu }$, ${\displaystyle d}$) ${\displaystyle (X,\mu ,d)}$은 미터법 측정 공간이며, X는 미터법 d를 가진 미터법 공간이고, μ는 X에 대한 보렐 측정 공간이다. X의 측정 가능한 부분 집합 A의 경계 측도 또는 Minkowski 함량은 림 inf로 정의된다.

${\displaystyle \mu ^{+}(A)=\liminf _{\varepsilon \to 0+}{\frac {\mu(A_{\barepsilon }-\mu(A)}{\barepsilon },}},}$

어디에

${\displaystyle A_{\barepsilon }=\{x\in X d(x,A)\leq \varepsilon \}}$

A의 ε 연장이다.

X의 등거리계 문제는 주어진 μ(A)에 대해 $\mu {\displaystyle {}^{}}$+${\displaystyle {}^{}}$( A${\displaystyle }$) ${\displaystyle \mu ^{+}(A)}$이(가) 얼마나$$ 작을 수 있는지 묻는다. 만약 X가 통상적인 거리를 가진 유클리드 평면과 르베그 측도라면, 이 질문은 비록 답은 같지만, 경계가 반드시 매끄럽지 않은 평탄한 지역에 고전적인 등거리 문제를 일반화한다.

함수

$\displaystyle I(a)=\inf\{\mu ^{+}(A) \mu(A)=a\}}}$

미터법 측정 공간의 등측량 프로파일$({\displaystyle X}$, ${\displaystyle \mu }$, d${\displaystyle }$) ${\displaystyle (X,\mu ,d)}$이라고 불린다$.$ 등측량 프로파일은 이산 그룹의 케이리 그래프와 리만 다지관의 특수 등급(대개 일정한 경계를 가진 지역 A만 고려됨)에 대해 연구되어 왔다.

그래프의 경우

그래프 이론에서, 등가속적 불평등은 강한 연결 특성을 가진 희박한 그래프인 확장형 그래프 연구의 핵심이다. 익스팬더 구조는 복잡성 이론, 강력한 컴퓨터 네트워크의 설계, 오류 수정 이론에 대한 여러 응용과 함께 순수 및 응용 수학에 대한 연구를 낳았다.^[7]

그래프의 등차측 불평등은 정점 하위 집합의 크기와 경계 크기를 연관시킨다. 이 값은 대개 부분 집합(에지 확장)에서 나가는 가장자리 수 또는 인접한 정점 수(버텍스 확장)로 측정된다. 그래프 $G{\displaystyle }$ ${\displaystyle G}$ 및$$ $숫자{\displaystyle }$ k ${\displaystyle k}$의 경우$,$ 다음은 그래프에 대한 두 가지 표준 등거리측정 파라미터다.^[8]

• 모서리 등측위 파라미터:

${\displaystyle \Phi \{E}(G,k)=\min _{S\subseteq V}\left\{E(S,{\overline {S}) : S =k\오른쪽\}}$

• 정점 등거리 파라미터:

${\displaystyle \Phi \{V}(G,k)=\min _{S\subseteq V}\left\{\Gamma(S)\setminus S : S =k\right\}}}}$

Here ${\displaystyle E(S,{\overline {S}})}$ denotes the set of edges leaving ${\displaystyle S}$ and ${\displaystyle \Gamma (S)}$ denotes the set of vertices that have a neighbour in ${\displaystyle S}$. The isoperimetric problem consists of understanding how the parameters ${\displ$$aystyle \Phi _{E}$ 및$$ ${\displaystyle {\phi }_{}}$ V ${\$는 그래프의 자연 패밀리에 대해 동작한다$$.

예: 하이퍼큐브에 대한 등차측 불평등

The ${\displaystyle d}$-dimensional hypercube ${\displaystyle Q_{d}}$ is the graph whose vertices are all Boolean vectors of length ${\displaystyle d}$, that is, the set ${\displaystyle \{0,1\}^{d}}$. Two such vectors are connected by an edge in ${\displaystyle Q_{d}}$ if they are eq한 비트 플립, 즉 해밍 거리가 정확히 1이다. 다음은 부울 하이퍼큐브에 대한 이등법적 불평등이다.^[9]

모서리 등측 부등식

하이퍼큐브의 가장자리 등측불평등은 $\phi {\displaystyle {\mathrm{}}_{}{E}_{}}$ (${\displaystyle Q_{}}$d ,${\displaystyle k}$ )${\displaystyle k}$k (${\displaystyle d_{}}$- ${\displaystyle {log\mathrm{}}_{}}$ 2${\displaystyle {}_{}k}$k ) ${\displaystyle \Phi _{E}(Q_{d}k)\geq$ k$(d-\log _{2$}k$)$이다$.$ $Q{\displaystyle {}_{}}$ ${\displaystyle d_{}}$ ${\$의 서브큐브 정점 집합인$$ 각 세트 $S{\displaystyle }$ ${\dapplaystyle S}$에서 볼 수 있듯이 이 바운드는 단단하다$.$

등점 부등식

하퍼의 정리는^[10] 해밍 볼이 주어진 크기의 모든 세트 중에서 가장 작은 정점 경계를 가지고 있다고 말한다. 해밍 볼은 $최대{\displaystyle }$ $r{\displaystyle }$ ${\displaystyle r}$에서 해밍 중량의 모든 점을 포함하고$$ 일부 정수 r {\$displaystyle r}$에 대해 ${\displaystyle \mathrm{r}}$+ 1 ${\displaystyle r+1}$보다 큰 해밍 중량의 점이 없는 세트다$.$ 이 정리는 S $with{\displaystyle }$ ${\displaystyle V}$ ${\displaystyle S\subseteq V}$을(를) 포함하는$$ 모든 세트 S ${\displaystyle \subseteq }$ V를 의미한다.

${\displaystyle S \geq \sum _{i=0}^{r}{d \선택 i}}$

만족시키다

${\d 디스플레이 스타일 S\cup \Gamma (S) \geq \sum _{i=0}^{r+1}{d \do \선택 i}}$^[11]

특별한 경우, 폼의$$ $k{\displaystyle }$= ${\displaystyle S}$ $displaystyle k=$ S $}$ 크기를 고려하십시오.

${\displaystyle k={d \선택 0}+{d \선택 \1}+\ft +{d \선택 r}}$

일부 정수 $r{\displaystyle }$ ${\displaystyle r}$에 대해$$위와 같이 정확한 정점 isoperimetric 매개 변수가

${\displaystyle \Phi _{V}(Q_{d}}k)={d \선택 r+1}}$^[12]

삼각형에 대한 등측위 부등식

둘레 p와 면적 T에 대한 삼각형의 등차계 불평등은 다음과^[13][14] 같이 명시되어 있다.

${\displaystyle p^{2}\geq 12{\sqrt{3}}\cdot T,}$

등변 삼각형과 동등하게 이는 AM-GM 불평등을 통해 삼각형에 대한 등측 불평등이라고도 불리는 더 강한 불평등에 의해 암시된다.^[15]

${\displaystyle T\leq {\frac {\sqrt{3}}{4}}(abc)^{\frac {2}{3}}.}$

참고 항목

• 블래쉬케-레베그 정리
• 채플린 문제
• 곡선단축유동
• 익스팬더 그래프
• 가우스 등분포 부등식
• 등거리 치수
• 등측점
• 삼각 불평등 목록
• 평면 분리 정리
• 혼합 볼륨

메모들

참조

외부 링크

위키미디어 커먼즈에는 이오페리메트릭 불평등과 관련된 미디어가 있다.

• 수렴에서의 등측위 문제의 역사
• Treiberg: 이등분포 부등식의 증거
• 이등분계 정리