Lanczos 재샘플링

크기 매개 변수가 1(위), 2(중간), 3(아래)인 이산 신호(검은 점)와 Lanczos 보간(파란색 단색 곡선)의 부분 플롯입니다.또한 Lanczos 커널의 두 복사본이 샘플 4와 11(대시 곡선)에 대응하여 이동 및 확장되어 있습니다.

Lanczos 필터링과 Lanczos 재샘플링은 수학 공식의 두 가지 응용 프로그램입니다.저역 통과 필터로 사용하거나 샘플 간의 디지털 신호 값을 부드럽게 보간하는 데 사용할 수 있습니다.후자의 경우 주어진 신호의 각 샘플을 Lanczos 커널의 변환된 스케일링된 복사본에 매핑합니다.이것은 두 번째 긴 sync 함수의 중앙 로브에 의해 윈도우에 표시되는 sync 함수입니다.다음으로 변환된 커널과 스케일링된 커널의 합계를 원하는 포인트로 평가합니다.

Lanczos 재샘플링은 일반적으로 디지털 신호의 샘플링 속도를 높이거나 샘플링 간격의 일부만 이동시키기 위해 사용됩니다.디지털 이미지의 크기 조정 또는 회전과 같은 다변량 보간에도 자주 사용됩니다.이 목적을 ^[1]위한 몇 가지 단순한 필터 중 "최상의 타협"으로 간주되어 왔습니다.

필터의 이름은 발명가인 Cornelius Lanczos(헝가리어 발음: [la͡ntʃso])의 이름을 따서 지어졌다.

정의.

란초스 커널

= 1, 2, 3용 Lanczos 창.

a = 2 및 a = 3의 경우 Lanczos 커널.함수는 음의 값을 얻습니다.

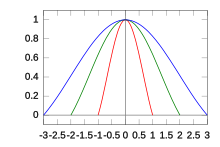
보간된 값에 대한 각 입력 샘플의 효과는 Lanczos 커널이라고 하는 필터의 재구성 $커널$ L $(x)$ 에 의해 정의됩니다.이는 Lanczos 창 또는 $-a x$ x $a$ a에 대해 수평으로 늘어나는 sync $(x / a)$ 기능의 $중심$ 로브인 sync(x/a) 창으로 창(승수)을 이루는 정규화된 sync $(x) 함수$ 입니다.

L(x)=operatorname {case}(\pi x)\operatorname {cases}(\pi x/a)&{\text {if})\a<x,\0&{\text{cases}}.\end {case}

마찬가지로

L(x)=begin{case}1&{\text{if}\x=0,\{\dfrac {a\sin(\pi x)\sin(\pi x)\sin(\pi x)}{\pi ^{2}}&{\text{if}\a\leq}\ne x<\ne},\end {case}

$파라미터$ a는 커널의 크기를 결정하는 양의 정수(일반적으로 2 또는 3)입니다.Lanczos 커널은 중앙에 양(+)의 2a- $1개$ 의 엽과 양 $(+)$ 의 엽을 각각 1개씩 가지고 $있습니다$ .

보간 공식

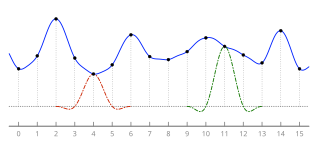
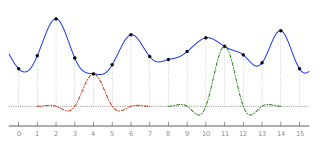
$샘플 i$ s를 가진 1차원 신호가 주어졌을 때, $i$ 의 정수 값에 대해 임의의 $실수$ 인수 x에서 $보간된$ 값 $S ($ x)는 Lanczos ^[2]커널을 사용한 샘플의 이산적인 합성에 의해 구해진다.

({displaystyle S(x)=\sum _{i=\lfloor x\cloor -a+1}^{\lfloor x\cloor +a}s_{i}L(x-i)}}}

$여기$ 서 a는 필터 크기 파라미터, $\lfloor x\rfloor$ " $"$ (\ $displaystyle\lfloor$ x $\loor)$ 는 $\lfloor x \rfloor$ 플로어 함수입니다.이 합계의 한계는 커널이 그 밖의 0이 되도록 되어 있습니다.

특성.

$매개$ 변수 a가 양의 정수인 한, Lanczos 커널은 어디에서나 연속적이며, 그 도함수는 정의되고 어디에서나 연속됩니다(두 sinc 함수가 모두 0이 되는 x $=$ ± $a$ 에서도 마찬가지입니다.따라서 재구성된 $신호$ S $(x)$ 도 연속 도함수를 갖는 연속 신호입니다.

Lanczos 커널은 값이 $1인$ x = $0$ 을 제외하고 모든 정수 $인수$ x에서 0입니다.따라서 재구성된 신호는 주어진 샘플을 정확하게 보간합니다. 모든 정수 $인수$ x = i에 $대해$ $S (x)$ = $s$ 가_i 됩니다.

다차원 보간법

흑백 이미지의 시작입니다.JPEG 아티팩트를 사용한 원래의 저품질 확장.

동일한 영상이 Lanczos 재샘플링을 사용하여 각 방향의 5배 샘플로 재샘플링됩니다.픽셀화 아티팩트가 제거되어 영상의 전송 기능이 변경되었습니다.

Lanczos 필터의 2차원 커널은

L(x,y)=L(x)L(y).

평가하기

이점

개별 Lanczos 창 및 해당 주파수 응답. 다른 창과 비교하려면 창 기능을 참조하십시오.

밴드 제한 신호에 대해 이론적으로 최적의 재구성 필터는 무한 지원을 제공하는 sync 필터입니다.Lanczos 필터는 sync 필터의 실제적인 근사치(최종적으로 지원되는) 중 하나입니다.보간된 각 값은 $연속$ 된 2a 입력 샘플의 가중치 합입니다.따라서 $2a$ 파라미터를 변경함으로써 주파수 응답 개선을 위해 연산 속도를 교환할 수 있습니다.또한 모수를 사용하면 데이터에 더 부드러운 보간 또는 날카로운 과도 상태를 보존할 수 있습니다.이미지 처리의 경우 앨리어싱 아티팩트의 감소와 날카로운 모서리의 보존 사이의 트레이드오프입니다.또한 이러한 처리와 마찬가지로 이미지의 테두리에 대한 결과는 없습니다.커널 길이를 늘리면 이미지의 가장자리가 잘립니다.

Lanczos 필터는 이산 신호에 대한 다른 보간 방법, 특히 동기 필터의 다른 윈도우 버전과 비교되었습니다.Turkowski와 Gabriel은 2차원 영상 ^[1]데이터의 소멸과 보간 처리를 위해 잘린 sync와 바틀렛, 코사인, 한 창 sync와 비교하여 ( $a$ = 2) Lanczos 필터가 "에일리어싱, 선명도 및 최소 호출음의 감소 측면에서 최선의 타협"이라고 주장했다.Jim Blinn에 따르면, Lanczos 커널 $(= 3$ )은 "지금까지 ^[3]본 어떤 (불가능한) 필터보다 저주파를 더 잘 제거하고 높은 주파수를 거부합니다."

Lanczos 보간은 AviSynth^[4] 및 FFmpeg와 ^[5]같은 다양한 미디어 유틸리티에서 비디오를 "업스케일링"하기 위해 널리 사용되는 필터입니다.

제한 사항

커널은 a > $1$ 에 $대해$ 음의 값을 가정하기 때문에 모든 샘플이 양일 경우에도 보간 신호가 음이 될 수 있습니다.보다 일반적으로 보간 신호의 값 범위는 이산 샘플 값에 의해 확장된 범위보다 넓을 수 있다.특히 샘플 값이 갑자기 변경되기 직전과 직후에 호출음 아티팩트가 있을 수 있으며, 이로 인해 클리핑 아티팩트가 발생할 수 있습니다.단, 이러한 효과는 (창이 없는) 동기 필터에 비해 감소합니다.a = 2(3개의 로브 커널)의 경우 링잉은 1% 미만입니다.

이 메서드는 무료 소프트웨어 GNU 이미지 조작 프로그램(GIMP)에서 사용할 수 있는 보간 옵션 중 하나입니다.호출음 효과를 시각화하는 한 가지 방법은 흑백 블록 그래픽의 스케일을 조정하고 Lanczos 보간을 선택하는 것입니다.

이미지 재샘플링에 Lanczos 필터를 사용하는 경우 링잉 효과로 인해 강한 가장자리를 따라 밝고 어두운 할로우가 생성됩니다.이러한 대역은 시각적으로 귀찮을 수 있지만 인식되는 선명도를 높이는 데 도움이 되므로 가장자리 강화의 한 형태를 제공합니다.이렇게 하면 ^[6]시야에서 모서리 선명도의 특수 역할을 할 경우 이미지의 주관적 품질이 향상될 수 있습니다.

일부 응용 프로그램에서는 필터링 전에 데이터를 로그 도메인으로 변환함으로써 로우엔드 클리핑 아티팩트를 개선할 수 있습니다.이 경우 보간된 값은 입력 샘플의 산술 평균이 아닌 가중 기하 평균이 됩니다.

Lanczos 커널에는 unity 속성 파티션이 없습니다.즉, 커널의 모든 정수 변환 복사본의 U ${\textstyle U(x)=\sum _{i\in \mathbb {Z} }L(x-i)}$ $=$ i ${\textstyle U(x)=\sum _{i\in \mathbb {Z} }L(x-i)}$ Z ${\textstyle U(x)=\sum _{i\in \mathbb {Z} }L(x-i)}$ ${\textstyle U(x)=\sum _{i\in \mathbb {Z} }L(x-i)}$ ) { $textstyle$ U $(x$ )=\ $sum$ _ ${i\in \mathbb {Z}}L(x-i)}$ 의 ${\textstyle U(x)=\sum _{i\in \mathbb {Z} }L(x-i)}$ ${\textstyle U(x)=\sum _{i\in \mathbb {Z} }L(x-i)}$ 이 항상 1은 아니다.따라서 상수 샘플이 있는 이산 신호의 Lanczos 보간은 상수 함수를 생성하지 않습니다.이 결점은 a = $1일$ 때 가장 뚜렷합니다.또한 a = $1$ 의 $경우$ , 보간된 신호는 모든 정수 인수에 0 도함수를 가집니다.단일 프로세서 커널(a = 1)을 사용하면 Lanczos 접근 방식의 이점을 모두 잃고 필터가 제대로 제공되지 않으므로 이는 다소 학술적입니다.더 나은 단일 로브, 종 모양의 윈도우 기능이 많이 있습니다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b Turkowski, Ken; Gabriel, Steve (1990). "Filters for Common Resampling Tasks". In Glassner, Andrew S. (ed.). Graphics Gems I. Academic Press. pp. 147–165. CiteSeerX 10.1.1.116.7898. ISBN 978-0-12-286165-9.
^ Burger, Wilhelm; Burge, Mark J. (2009). Principles of digital image processing: core algorithms. Springer. pp. 231–232. ISBN 978-1-84800-194-7.
^ Blinn, Jim (1998). Jim Blinn's corner: dirty pixels. Morgan Kaufmann. pp. 26–27. ISBN 978-1-55860-455-1.
^ "Resize". Avisynth. 2015-01-01. Retrieved 2015-07-27.
^ "A How To guide: Upconverting video using FFDShow - Neowin Forums". Neowin.net. 2006-04-18. Retrieved 2012-07-31.
^ "IPOL: Linear Methods for Image Interpolation". Ipol.im. 2011-09-27. Retrieved 2012-07-31.

외부 링크

안티그레인 지오메트리의 예:image_filters.cpp에 다양한 커널을 사용하여 이미지를 반복적으로 재샘플링하는 경우의 비교를 나타냅니다.
image resampler: C++의 퍼블릭도메인 이미지 재샘플링 클래스.창이 있는 여러 Lanczos 필터 커널을 지원합니다.

[turkgab-1] Turkowski, Ken; Gabriel, Steve (1990). "Filters for Common Resampling Tasks". In Glassner, Andrew S. (ed.). Graphics Gems I. Academic Press. pp. 147–165. CiteSeerX 10.1.1.116.7898. ISBN 978-0-12-286165-9.

[burger-2] Burger, Wilhelm; Burge, Mark J. (2009). Principles of digital image processing: core algorithms. Springer. pp. 231–232. ISBN 978-1-84800-194-7.

[3] Blinn, Jim (1998). Jim Blinn's corner: dirty pixels. Morgan Kaufmann. pp. 26–27. ISBN 978-1-55860-455-1.

[4] "Resize". Avisynth. 2015-01-01. Retrieved 2015-07-27.

[5] "A How To guide: Upconverting video using FFDShow - Neowin Forums". Neowin.net. 2006-04-18. Retrieved 2012-07-31.

[6] "IPOL: Linear Methods for Image Interpolation". Ipol.im. 2011-09-27. Retrieved 2012-07-31.

[1]

[2]

[3]

[4]

[5]

[6]

Search

Lanczos 재샘플링

네임스페이스

더

목차

정의.

란초스 커널

보간 공식

특성.

다차원 보간법

평가하기

이점

제한 사항

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

Lanczos 재샘플링

정의.

란초스 커널

보간 공식

특성.

다차원 보간법

평가하기

이점

제한 사항

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.