창 기능
Window function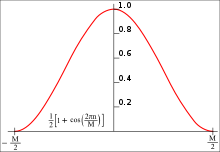
신호 처리 및 통계에서 창 함수(apodization 함수 또는 테이퍼링 함수로도[1] 알려져 있음)는 일부 선택된 구간을 벗어나 영점 값을 갖는 수학적 함수로서, 일반적으로 구간의 중간을 중심으로 대칭되며, 보통 중간에서 최대치에 가깝고, 보통 중간에서 테이퍼링하여 중간에서 테이퍼링한다. 수학적으로 다른 함수나 파형/데이터 시퀀스가 윈도우 함수에 의해 "복제"될 때, 제품 또한 간격 바깥에 영점화된다. 남은 것은 그것들이 겹치는 부분, 즉 "창을 통한 보기"가 전부다. 동등하게, 그리고 실제로, 윈도우 내의 데이터 세그먼트는 먼저 격리된 다음, 그 데이터에만 윈도우 기능 값을 곱한다. 따라서 분할이 아닌 테이퍼링은 윈도우 기능의 주요 목적이다.
더 긴 기능의 세그먼트를 검사하는 이유로는 과도현상 검출과 주파수 스펙트럼의 시간 평균화가 있다. 세그먼트의 지속시간은 시간 및 주파수 분해능과 같은 요건에 의해 각 애플리케이션에서 결정된다. 그러나 그 방법은 또한 스펙트럼 누설이라는 효과에 의해 신호의 주파수 함량을 변화시킨다. 창문 기능은 특정 용도의 필요에 따라 다양한 방법으로 누설점을 분산시킬 수 있게 해준다. 이 글에는 여러 가지 선택이 상세하게 설명되어 있지만, 그 차이점들 중 상당수는 실제로 대수롭지 않을 정도로 미묘하다.
일반적인 애플리케이션에서 사용되는 윈도우 기능은 음이 아닌 부드러운 "벨 모양" 곡선이다.[2] 직사각형, 삼각형, 그리고 다른 기능들도 사용될 수 있다. 윈도우 기능의 보다 일반적인 정의는 윈도우의 곱에 그 인수를 곱한 윈도우의 제품이 정사각형 통합이 가능한 한, 그리고 더 구체적으로는 함수가 0을 향해 충분히 빠르게 가는 한, 그것들은 구간 밖에서 동일하게 0이 될 필요가 없다.[3]
적용들
창 기능은 스펙트럼 분석/수정/재합성, 유한 임펄스 반응 필터 설계,[4] 빔포밍 및 안테나 설계에 사용된다.
스펙트럼 분석
함수 cos(Ωt)의 푸리에 변환은 주파수 ±Ω을 제외하고 0이다. 그러나 다른 많은 기능과 파형은 편리한 폐쇄형 변환을 가지고 있지 않다. 또는 특정 시간 동안에만 스펙트럼 함량에 관심이 있을 수 있다.
어느 경우든 푸리에 변환(또는 유사한 변환)은 파형의 하나 이상의 유한한 간격에 적용할 수 있다. 일반적으로 변환은 파형 및 윈도우 기능에 적용된다. 모든 창(사각형 포함)은 이 방법에 의해 계산된 스펙트럼 추정치에 영향을 미친다.

창 기능 선택
cos(Ωt)와 같은 단순 파형의 윈도우 설정은 Ω이 아닌 주파수에서 푸리에 변환의 0이 아닌 값(일반적으로 스펙트럼 누설)을 발생시킨다. 누출은 Ω에 가까운 최악의 (최고) 경향이 있으며 최소한 Ω에서 가장 먼 주파수에서 발생한다.
분석 중인 파형이 서로 다른 주파수의 사인파 두 개로 구성되면 누출이 이를 시각적으로 구별하는 데 방해가 될 수 있다. 가능한 유형의 간섭은 종종 다음과 같이 두 개의 반대되는 등급으로 나뉜다. 구성 요소 주파수가 서로 다르고 한 구성 요소가 약한 경우, 더 강한 구성 요소에서 누출되면 더 약한 구성 요소의 존재가 가려질 수 있다. 그러나 주파수가 너무 비슷하면 정현악이 동일 강도에 있는 경우에도 누설로 인해 분해할 수 없게 된다. 첫 번째 유형의 간섭, 즉 구성요소가 서로 다른 주파수와 진폭을 갖는 윈도우를 하이 다이내믹 레인지라고 한다. 반대로 주파수와 진폭이 비슷한 성분을 구별할 수 있는 창을 고해상도라고 한다.
직사각형 창은 해상도는 높지만 동적 범위는 낮은 창문의 예로서, 주파수 역시 가까울 때도 비슷한 진폭의 구성요소를 구분하는데 좋으나 주파수가 멀리 떨어져 있어도 다른 진폭의 구성요소를 구분하는데 서툴다는 것을 의미한다. 직사각형 창문과 같은 고해상도 저동적 창도 고감도 특성을 가지고 있는데, 이는 첨가 무작위 노이즈가 있는 곳에서 상대적으로 약한 정현상을 드러내는 능력이다. 소음이 고해상도 창보다 고다이내믹 레인지 창으로 더 강한 반응을 일으키기 때문이다.
윈도우 유형의 다른 극단에는 동적 범위가 높지만 해상도와 감도가 낮은 윈도우가 있다. 고동적 범위 창은 광대역 애플리케이션에서 가장 흔히 정당화되며, 분석되는 스펙트럼에는 다양한 진폭의 다양한 구성 요소가 포함될 것으로 예상된다.
극단의 중간에는 해밍과 한과 같은 적당한 창문이 있다. 그것들은 전화 채널의 스펙트럼과 같은 협대역 어플리케이션에서 일반적으로 사용된다.
요약하면, 스펙트럼 분석은 유사한 주파수(고해상도/감도)로 비교 가능한 강도 요소 해결과 상이한 주파수(고동적 범위)로 상이한 강도 요소 해결 사이의 절충을 포함한다. 그러한 절충은 윈도우 기능이 선택되었을 때 발생한다.[5]: p. 90
이산 시간 신호
입력 파형이 연속이 아닌 시간 샘플링된 경우 대개 윈도우 기능을 적용한 다음 이산 푸리에 변환(DFT)을 적용하여 분석을 수행한다. 그러나 DFT는 실제 이산 시간 푸리에 변환(DTFT) 스펙트럼의 희박한 샘플링만 제공한다. 그림 2, 3열은 직사각형 창 사인파에 대한 DTFT를 보여준다. 사인파의 실제 주파수는 수평축에 "13"으로 표시된다. 다른 것은 모두 누설이고, 로그 프리젠테이션의 사용으로 과장되었다. 주파수 단위는 "DFT 빈"이다. 즉, 주파수 축의 정수 값은 DFT에 의해 샘플링된 주파수에 해당한다. 따라서 그림에는 사인파의 실제 주파수가 DFT 샘플과 일치하고 스펙트럼의 최대값이 해당 샘플에 의해 정확하게 측정되는 경우를 묘사한다. 4행에서는 ½ bin에 의해 최대값을 놓치고, 그 결과 발생하는 측정 오차를 가리비 손실(피크의 형상에 의해 발생)이라고 한다. 음악 노트나 사인파 테스트 신호와 같이 알려진 주파수의 경우, 주파수를 DFT bin에 일치시키는 것은 샘플링 속도 및 창 길이의 선택에 의해 미리 정렬될 수 있으며, 윈도우 내에 정수 수의 사이클이 발생한다.
노이즈 대역폭
해상도와 동적 범위의 개념은 사용자가 실제로 무엇을 하려고 하는가에 따라 다소 주관적인 경향이 있다. 그러나 그들은 또한 계량 가능한 총 누출과 높은 상관관계를 가지는 경향이 있다. 보통 등가 대역폭인 B로 표현된다. DTFT를 스펙트럼 최대값과 폭 B와 동일한 높이로 직사각형 모양으로 재분배한다고 생각할 수 있다.[A][6] 누설량이 많을수록 대역폭도 커진다. 입력 신호에 무작위 노이즈 성분(또는 무작위 노이즈일 뿐)이 포함되어 있을 때 각 DFT bin에 의해 등록될 평균 전력에 비례하기 때문에 노이즈 등가 대역폭 또는 등가 노이즈 대역폭이라고 부르기도 한다. 시간 경과에 따른 평균으로 출력 스펙트럼의 그래프는 일반적으로 이 효과로 인해 발생하는 평평한 소음층을 나타낸다. 소음층의 높이는 B에 비례한다. 그래서 두 개의 서로 다른 윈도우 기능이 다른 층을 만들 수 있다.
처리손익
신호 처리에서, 신호와 부패한 영향 사이의 차이를 이용하여 신호 품질의 일부 측면을 개선하기 위해 작동을 선택한다. 신호가 부가적인 무작위 노이즈에 의해 손상된 사인파인 경우 스펙트럼 분석은 신호와 노이즈 성분을 다르게 분산시켜 신호의 존재를 쉽게 감지하거나 진폭과 주파수와 같은 특정 특성을 측정하는 것을 용이하게 한다. 효과적으로, 신호 대 잡음비(SNR)는 한 주파수를 중심으로 대부분의 사인파 에너지를 집중시키면서 소음을 균일하게 분산시켜 개선한다. 처리 이득은 SNR 개선을 설명하기 위해 자주 사용되는 용어다. 스펙트럼 분석의 처리 이득은 윈도우 기능, 즉 노이즈 대역폭(B)과 잠재적 가리비 손실 모두에 따라 달라진다. 이러한 효과는 부분적으로 상쇄되는데, 이는 가리비가 가장 적게 표시된 창문이 자연적으로 가장 많이 누출되기 때문이다.
그림 3은 3개의 서로 다른 창 함수가 동일한 데이터 집합에 미치는 영향을 나타내며, 가법 노이즈에서 2개의 동일한 강도 사인파(syngoid)로 구성된다. 사인파의 주파수는 가리비를 마주치지 않고, 다른 하나는 최대 가리비를 마주치도록 선택된다. 두 사인파 모두 블랙먼-해리스 창보다 한 창 아래에서 SNR 손실이 적다. 일반적으로(앞에서도 언급했듯이), 이것은 저동적 어플리케이션에서 고동적 범위 윈도우를 사용하는 것을 억제하는 것이다.
대칭
이 문서에서 제공하는 공식은 마치 연속적인 윈도우 기능이 "샘플링"된 것처럼 별개의 시퀀스를 생성한다(Kaiser 창의 예시 참조). 스펙트럼 분석을 위한 윈도우 시퀀스는 대칭이거나 대칭에 1-표본 부족이다(주기적이라 [7][8]함,DFT-짝수 또는 DFT-대칭[9]: p. 52 ). 예를 들어, 단일 중앙점에서 최대값을 갖는 진정한 대칭 시퀀스는 MATLAB 함수에 의해 생성된다. hann(9,'symmetric')마지막 샘플을 삭제하면 hann(8,'periodic'). 이와 유사하게, 순서 hann(8,'symmetric') 두 개의 같은 중앙점을 가지고 있다.[10]
일부 함수는 영점값이 매겨진 엔드포인트를 한두 개 가지고 있는데, 대부분의 어플리케이션에서는 불필요하다. 제로 값 엔드포인트를 삭제해도 DTFT(스펙트럼 누출)에는 영향이 없다. 그러나 한쪽 또는 양쪽 끝점을 모두 삭제할 것으로 예상하여 N + 1 또는 N + 2 표본을 위해 설계된 함수는 일반적으로 약간 좁은 주엽, 약간 높은 측면부 및 약간 작은 소음 대역폭을 가진다.[11]
DFT-대칭
DFT의 전신은 유한 푸리에 변환이며, 윈도 기능은 "항상 홀수 포인트로 원점에 대한 균일한 대칭성을 나타낸다"[9]: p.52 고 한다. 그 경우 DTFT는 완전히 실제 가치로 평가된다. 동일한 시퀀스 DFT 데이터 창으로 이동할 때 N{N\displaystyle}-length DFT 봤을,[0≤ n≤ N], DTFT이 주파수 1/N의 규칙적으로 간격을 제외하고는 complex-valued. 따라서,{1/N\displaystyle.}[를]{\displaystyle[0\leq Nn\leq],}, 표본들은(DFT 계수라고 불리는) 있다. s실물 가치까지 근사치는 N+1 길이 시퀀스(으로 [ N = 0 를 잘라내고 - 길이 DFT를 계산하는 것이다. DTFT(스펙트럼 누출)는 약간 영향을 받지만 표본은 실제 값을 유지한다.[12][B] DFT-짝수 및 주기적 용어란 잘린 시퀀스를 주기적으로 반복하면 = 에 대해 짝수 대칭이 되며 DTFT의 DTFT는 완전히 실제 값을 갖는다는 생각을 말한다. 그러나 실제 DTFT는 DFT 계수를 제외하고 일반적으로 복잡하게 값을 매긴다. 후속 섹션에서는 DTFT를 훨씬 더 조밀하게 샘플링하고 복잡한 숫자의 크기 성분만 표시한다.
주기 합계
/ N 의 간격으로 N+1 길이 시퀀스의 DTFT를 샘플링하는 정확한 방법은 DTFT § L=N+1에 설명되어 있다. 기본적으로 [ 은(는) [ 추가적으로)와 결합되며, 잘린 순서에서 -point DFT가 수행된다. 마찬가지로 스펙트럼 분석은 대칭 윈도우를 적용하기 전에 = 0 과 = 데이터 샘플을 결합하여 수행될 것이다. 잘린 창문이 매우 인기가 있지만, 그것은 흔한 관습이 아니다.[9][13][14][15][16][17][b]
콘볼루션
DFT-대칭 창문의 매력은 홀수 길이 시퀀스를 잘라내면 짝수 길이 시퀀스가 되기 때문에 DFT 구현을 위한 FFT(Fast Fourier Transform) 알고리즘의 인기에 의해 설명된다. 그들의 실제 가치 DFT 계수는 또한 DFT 계수와 데이터의 자유로운 DFT 사이의 경합을 통해 윈도우 설정이 달성되는 특정 난해한 애플리케이션에서도[C] 장점이다.[18][9]: p.62 [5]: p.85 그러한 애플리케이션에서는 대부분의 DFT 계수가 영(0) 값이므로 콘볼루션을 매우 효율적으로 만들기 때문에 코사인섬 계열의 DFT 대칭 창(짝수 또는 홀수 길이)이 선호된다.[D][5]: p.85
필터 디자인
윈도우는 디지털 필터의 설계에, 특히 sinc 함수와 같은 무한 지속시간의 "이상적인" 충동 응답을 유한 충동 응답(FIR) 필터 설계로 변환하는 데 이용되기도 한다. 그것을 창법이라고 한다.[19][20][21]
통계 및 곡선 적합
윈도우 함수는 때때로 곡선의 부분으로부터 멀리 떨어진 지점의 영향을 감소시키는 가중 요인과 함께 분석되는 데이터 집합을 특정 지점 근처의 범위로 제한하기 위해 통계 분석 분야에서 사용된다. 베이시안 분석과 곡선 적합의 분야에서는 이것을 흔히 커널이라고 한다.
직사각형 창 적용
과도현상 분석
에너지 대 시간 분포가 극히 고르지 않은 임펄스, 충격 응답, 사인 버스트, 처프 버스트 또는 노이즈 버스트와 같은 모달 분석에서 과도 신호를 분석할 때 직사각형 윈도우가 가장 적합할 수 있다. 예를 들어, 대부분의 에너지가 기록 시작 부분에 위치할 때 직사각형이 아닌 창은 대부분의 에너지를 감쇠시켜 신호 대 잡음 비를 저하시킨다.[22]
조화해석
특정 악기에서 음의 고조파 함량 또는 주어진 주파수에서 증폭기의 고조파 왜곡을 측정하고자 할 수 있다. 그림 2를 다시 언급하면서, 우리는 DFT가 샘플링한 조화 관련 주파수 이산 집합에서 누설이 없음을 관찰할 수 있다. (스펙트럼 null은 실제로 제로 크로싱이며, 이와 같은 로그 스케일에서는 나타낼 수 없다.) 이 특성은 직사각형 창문에 고유하며, 위에서 설명한 것처럼 신호 주파수에 맞게 적절히 구성되어야 한다.
창 기능 목록
규약:
- () 은(는) 0 = 0 x로,[23] x [- / {\}에 대해 연속되며, 서은 양의 정수(짝수 또는 홀수이다.[24]
- 순서 { [ = ( - / ), n은 길이 + 1.의 대칭이다
- [ - n은(는) 길이가 인 DFT 대칭이다.
- 각 스펙트럼 그림에 표시되는 변수 B는 DFT 빈 단위로 표시되는 함수의 노이즈 등가 대역폭 측정 기준이다.
DTFT의 희박한 샘플링(그림 2의 DFT와 같은)은 주파수도 정수 DFT 빈인 사인파에서 DFT 빈으로의 누출만 보여준다. 보이지 않는 사이드로브는 다른 주파수에서 사인파로부터 예상할 수 있는 누설을 드러낸다.[c] 따라서 윈도우 기능을 선택할 때 일반적으로 DTFT를 더 촘촘하게 샘플링하고(이 절에서 수행하는 것처럼) 사이드로브를 허용 가능한 수준으로 억제하는 윈도우를 선택하는 것이 중요하다.
직사각형 창
직사각형 창(박스카 또는 디리클레 창이라고도 함)은 데이터 시퀀스의 N 값을 제외한 모든 값을 0으로 대체하여 파형이 갑자기 켜지거나 꺼지는 것처럼 보이게 하는 가장 단순한 창이다.
다른 창은 위에서 설명한 바와 같이 가리비 손실을 줄이고 동적 범위를 개선하는 이러한 갑작스러운 변화를 완화하도록 설계되어 있다(§ Spectrum 분석).
직사각형 창은 1차 B-스플라인 창과 0차 사인파 전원 창이다.
B-스플라인 창
B-스플라인 창문은 직사각형 창문의 K-폴드 경련으로 얻을 수 있다. 그것들은 직사각형 창문 그 자체(k = 1)와 § 삼각형 창문 (k = 2) 및 § 파젠 창문 (k = 4)을 포함한다.[25] 대체 정의는 이산 시간 창을 복잡하게 만드는 대신 적절한 정규화된 B-분할 기본 함수를 샘플링한다. k-orderth B-spline basis 함수는 직사각형 함수의 k-폴드 자가 합산을 통해 얻은 °k-1의 조각형 다항식 함수다.
삼각창
삼각형 창은 다음을 통해 제공된다.
여기서 L은 N,[26] N + 1 [9]또는 N + 2가 될 수 있다.[29] 첫 번째 창은 바틀렛 창이나 페제르 창으로도 알려져 있다. 세 가지 정의 모두 큰 N에서 수렴한다.
삼각형 창은 2차 B-스플라인 창이다. L = N 형태는 두 개의 N/2 폭의 직사각형 창문의 경련으로 볼 수 있다. 결과의 푸리에 변환은 반폭 직사각형 창의 변환 제곱 값이다.
파젠 창
L ≜ N + 1을 정의하면 de la Vallée Poussin 창이라고도 하는 Parzen 창은 다음에 의해 주어진 네 번째 순서 B-spline 창이다.[9]
기타 다항식 창
웰치창
Welch 창은 단일 포물선 섹션으로 구성된다.
정의 2차 다항식은 윈도우의 범위 밖에 있는 샘플에서 0의 값에 도달한다.
사인창
해당하는 ( ) 함수는 π/2 위상 오프셋이 없는 코사인 것이다. 그래서 사인창을[30] 코사인 창이라고도 한다.[9] 사인 함수의 반 사이클을 나타내기 때문에 반신 창 또는[31] 반신 창이라고도 한다.[32]
사인 창의 자기 상관은 보만 창이라고 알려진 함수를 생성한다.[33]
Sine/Cosine 창
이러한 창 기능은 다음과 같은 형태를 가지고 있다.[34]
직사각형 창(α = 0), 사인 창(α = 1) 및 Hann 창(α = 2)은 이 계열의 구성원이다.
짝수 α 값의 경우, 이러한 함수는 코사인섬 형태로도 표현할 수 있다.
코사인섬창
이 패밀리는 일반화된 코사인 창으로도 알려져 있다.
-
(Eq.1)
아래 예제를 포함한 대부분의 경우 모든 계수는 0k 0이다. 이러한 창은 2K + 1 비제로 N-포인트 DFT 계수에 불과하다.
Hann과 Hamming 창
사례 K = 1에 대한 관례적인 코사인섬 창은 다음과 같은 형식을 가지고 있다.
제로 위상 버전과 쉽게(흔히) 혼동된다.
=.5 설정.에서 Hann 창 생성:
쥴리어스 폰 헨의 이름을 따서 이름이 지어졌고, 때때로 해닝이라고 일컬어졌는데, 아마도 해밍 창과 언어적, 공식적 유사성 때문일 것이다. 0 위상 버전 ( n), 이(가) 상승 코사인 함수의 한 로브이기 때문에 상승 코사인이라고도 한다.
이 기능은 코사인섬(Cosine-sum)과 힘(Power-of-sine) 가족 모두의 구성원이다. 해밍 창과 달리, 한느 창문의 끝점이 0에 닿기만 한다. 그 결과로 생긴 측면 로브는 옥타브 당 약 18dB로 굴러간다.[35]
를 약 0.54로 설정하거나, 보다 정확하게 25/46으로 설정하면 Richard W. Hamming이 제안한 Hamming 창이 생성된다. 그 선택은 주파수 5㎛/(N - 1)에 제로크로싱을 배치하고, 이는 한남창의 첫 번째 사이드로비를 취소하며, 한남창의 약 5분의 1의 높이를 준다.[9][36][37] 해밍 윈도우는 맥박 형상에 사용될 때 흔히 해밍 블립이라고 불린다.[38][39][40]
소수점 이하 두 자리까지의 계수의 근사치는 거의 동일한 조건까지 사이드로브 수준을 상당히 낮춘다.[9][37] 등분포 감지에서 계수의 최적 값은 a0 = 0.53836, a = 01.46164이다.[37][5]
블랙맨 창
블랙맨 창은 다음과 같이 정의된다.
By common convention, the unqualified term Blackman window refers to Blackman's "not very serious proposal" of α = 0.16 (a0 = 0.42, a1 = 0.5, a2 = 0.08), which closely approximates the exact Blackman,[41] with a0 = 7938/18608 ≈ 0.42659, a1 = 9240/18608 ≈ 0.49656, and a2 = 1430/18608 ≈ 0.076849.[42] 이러한 정확한 값은 0을 세 번째와 네 번째 측면부에 배치하지만 가장자리에는 불연속성이 발생하고 6dB/10t의 낙차가 발생한다.[9] 잘린 계수는 사이드로브도 무효화하지 않고 18dB/10t 하강 효과가 개선되었다.[9][43]
너트형 윈도우, 연속 첫 번째 파생 모델
Nuttall 창 w ( ), 의 연속적인 형태와 그 첫 번째 파생상품은 Hann 함수처럼 도처에서 연속적으로 나타난다. 즉, 블랙맨-넛톨, 블랙맨-해리스, 해밍 윈도우와는 달리 x = ±N/2에서 기능이 0으로 간다. 블랙맨 창(α = 0.16) 역시 가장자리에 연속적인 파생상품이 존재하지만, "정확한 블랙맨 창"은 그렇지 않다.
블랙맨-넛틀 윈도우
블랙맨-해리스 창
사이드 로브 레벨을[44][45] 최소화하기 위한 시프트 싱크 기능을 추가함으로써 생성된 해밍 계열의 일반화
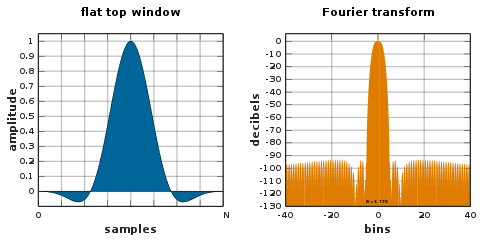
플랫 탑 윈도우
평평한 상단 창은 부분적으로 음수 값을 가진 창으로 주파수 영역에서 가리비 손실이 최소화된다. 이 특성은 정현상 주파수 성분의 진폭 측정에 바람직하다.[13][46] 넓은 대역폭의 단점은 낮은 주파수 분해능과 높은 § 노이즈 대역폭이다.
평평한 상단 창은 저역-통과 필터 설계 방법을 사용하여 설계할 [46]수 있거나 일반적인 코사인-섬 변형일 수 있다.
Matlab 변종에는 다음과 같은 계수가 있다.
주엽 근처에서 더 높은 값을 지불하고 굴러가는 사이드로브와 같은 다른 변형도 이용할 수 있다.[13]
라이프-빈센트 창
Rife-Vincent 창은[47] 단일 피크 값 대신 단일 평균 값을 위해 맞춤식으로 확장된다. Eq.1에 적용되는 아래의 계수 값은 그러한 관습을 반영한다.
I, 순서 1(K = 1): = 1 1= 기능적으로 Hann 창과 동일함.
클래스 I, 순서 2(K = 2): = = 4 = }={\ {4 {
클래스 I는 고차 사이드로브 진폭을 최소화하여 정의된다. K=4까지의 순서에 대한 계수는 표로 작성된다.[48]
클래스 II는 주어진 최대 측면 로브에 대한 주-로브 폭을 최소화한다.
클래스 III는 순서 K = 2가 § 블랙먼 윈도우와 유사한 절충안이다.[48][49]
조절식 창문
가우스 창
가우스인의 푸리에 변환도 가우스다. 가우스 함수의 지원은 무한대로 확장되기 때문에 창 끝에서 잘라내거나 또는 다른 제로 엔드 창으로 창 자체를 잘라야 한다.[50]
가우스 로그는 포물선을 생성하므로 주파수 추정에 있어 거의 정확한 2차 보간술에 사용할 수 있다.[51][50][52]
가우스 함수의 표준 편차는 σ · N/2 샘플링 주기이다.
제한된 가우스 창
제한된 가우스 창은 주어진 시간 폭(N + 1) σ에t 대해 가능한 가장 작은 루트 평균 제곱 주파수 폭 σ을ω 산출한다.[53] 이러한 창은 RMS 시간 주파수 대역폭 제품을 최적화한다. 그것들은 매개변수 의존 행렬의 최소 고유 벡터로 계산된다. 제한된 가우스 윈도우 패밀리는 각각 크고 작은 σ의t 제한 사례에서 § 사인 윈도우와 § 가우스 윈도우를 포함한다.
대략적으로 제한된 가우스 윈도우
L ≜ N + 1을 정의하면 시간 폭 L × σ의t 제한된 가우스 창은 다음과 같이 근사하게 된다.[53]
여기서 은(는) 가우스 함수:
대략적인t 창문의 표준 편차는 asy < 0.14에 대해 점증적으로 L × [53]×에 동일하다t(즉, N의 큰 값).
일반화 일반 창
가우스 창의 보다 일반화된 버전은 일반화된 일반 창이다.[54] 위의 가우스 창에서 표기법을 유지하면 이 창을 다음과 같이 나타낼 수 있다.
모든 에 = 2 에서은 가우스 창이며 p 이(가)approaches 에 근접함에 따라 직사각형 창에 근사하게 된다 이 창의 푸리에 변환은 p 을(를) 위해 닫힌 형태로 존재하지 않는다 그러나, 그것은 부드럽고 조절 가능한 대역폭의 다른 이점을 보여준다. § Tukey 창과 마찬가지로, 이 창은 자연스럽게 시계열의 진폭 감쇠를 제어하는 "플랫톱"을 제공한다(가우스 창으로는 컨트롤이 없다). 본질적으로 가우스 윈도우와 직사각형 윈도우 사이에 스펙트럼 누설, 주파수 분해능 및 진폭 감쇠 측면에서 양호한(제어 가능한) 절충을 제공한다. 이 창(또는 기능)의 시간 빈도 표현에 대한 연구도 참조하십시오.
투키 창
코사인 테이프가 있는 창이라고도 하는 Tukey 창은 너비 N(1 - α/2)의 직사각형 창과 융합되는 너비 Nα/2(스팬닝 Nα/2 + 1 관측치)의 코사인 로브로 간주할 수 있다.
α = 0에서는 직사각형이 되고, α = 1에서는 Hann 창이 된다.
플랑크 테이퍼 창
이른바 플랑크 테이퍼(Planck-taper) 창은 다지관의 일체성 칸막이 이론에 널리 사용되어[57] 온 범프 기능이다. 어디에나 부드럽지만( 함수) 콤팩트한 영역 밖에서는 정확히 0이며, 그 영역 내에서 한 간격에 걸쳐 정확히 1개씩이며, 그 한계 사이에 부드럽고 단조롭게 변화한다. 신호 처리에서 창 기능으로서의 그것의 사용은 플랑크 분포에서 영감을 받아 중력파 천문학의 맥락에서 처음 제안되었다.[58] 그것은 조각으로 정의된다.
테이퍼링의 양은 파라미터 ε에 의해 제어되며, 값이 작을수록 더 날카로운 전환을 제공한다.
DPSS 또는 Slepian 창
DPSS(분해 프로이트 스페이드로이드 시퀀스) 또는 슬레피언 윈도(Sleepian window)는 주엽의 에너지 농도를 극대화하며,[59] 스펙트럼의 잡음을 평균화하고 창 가장자리의 정보 손실을 줄이는 다층 스펙트럼 분석에 사용된다.
주엽은 파라미터 α에 의해 주어진 주파수 빈에서 끝난다.[60]
아래의 카이저 창은 DPSS 창과 간단한 근사치를 통해 생성된다.
카이저 창
카이저 또는 카이저-베셀 창은 제임스 카이저가 발견한 베셀 함수를 사용한 DPSS 창의 간단한 근사치다.[61][62]
여기서 는 첫 번째 종류의 0번째 순서 수정 Besel 함수다. 가변 파라미터 은 스펙트럼 누설 패턴의 주엽 폭과 측엽 레벨 사이의 트레이드오프를 결정한다. 주엽 너비는 null 사이의 2 + , ^{가 DFT 빈 단위로 주어지며,[69] }의 일반적인 값은 3이다.
돌프-체비셰프 창
주어진 주엽 너비에 대해 측면 로브의 체비셰프 규범을 최소화한다.[70]
[ 의 0 위상 돌프-체비셰프 창 함수는 대개 실제 값 이산 푸리에 변환 W [ 의 관점에서 정의된다[71]
Tn(x)는 x로 평가된 첫 번째 종류의 n번째 체비셰프 다항식이며, 이를 사용하여 계산할 수 있다.
그리고
()= 에 대한 고유한 양의 실제 용액이며 여기서 매개변수 α는 시들로의 체비셰프 규범을 -20 α 데시벨로 설정한다.[70]
창 함수는 역 이산0 푸리에 변환(DFT)에 의해 W(k)에서 계산할 수 있다.[70]
윈도우의 지연 버전은 다음을 통해 얻을 수 있다.
N의 짝수 값에 대해서는 다음과 같이 계산해야 한다.
즉, (- e + )의 역 DFT인 ( - π N + 1 ) k W ( k ) . {\lefte^{\이다.
변형:
- 에퀴리플 조건 때문에 시간 영역 창 가장자리에 불연속부가 있다. 에퀴리플이 가장자리에서 떨어지도록 함으로써 그들을 피하는 근사치는 테일러 창이다.
- 역 DFT 정의의 대안도 이용할 수 있다.[1].
울트라프구형창
울트라프구형 창은 1984년 로이 스트리트[72](Roy Streit)가 도입했으며 안테나 배열 설계,[73] 비복귀 필터 설계,[72] 스펙트럼 분석 등에 응용했다.[74]
다른 조정 가능한 창과 마찬가지로 울트라스포형 창에는 푸리에 변환 주-로브 폭과 상대 측면 로브 진폭을 제어하는 데 사용할 수 있는 매개변수가 있다. 다른 창에는 드물지만, 사이드 로브가 진폭을 감소(또는 증가)하는 속도를 설정하는 데 사용할 수 있는 추가 매개변수가 있다.[74][75][76]
창은 다음과 같이 시간 영역으로 표현할 수 있다.[74]
여기서 은(는) N의 Ultraspective 다항식이고, 과()μ {\ \은(는) 측면 로브 패턴을 제어한다.[74]
의 특정 값 은(는)[72] 잘 알려진 다른 창을 산출한다 μ 0 {\mu =0 및 = =1}은 돌프-체비셰프와 사라매키 창을 각각 부여한다. 다양한 파라메트리제이션이 있는 울트라스파이프 윈도우의 그림을 보려면 여기를 참조하십시오.
지수 또는 포아송 창
포아송 창, 또는 보다 일반적으로 기하급수적으로 기하급수적으로 창 중앙을 향해 증가하다가 후반에는 기하급수적으로 감소한다. 지수함수가 결코 0에 도달하지 않기 때문에, 그 한계에서 창 값은 0이 아니다(직사각형 창에 의한 지수함수의 곱셈으로 볼 수 있다). 에 의해 정의된다.
여기서 τ은 함수의 시간 상수다. 지수함수는 e ≃ 2.71828 또는 시간 상수당 약 8.69dB로 분해된다.[78] 즉, 윈도우 길이의 절반 이상 DdB의 목표 붕괴에 대해 시간 상수 by은 다음과 같이 주어진다.
하이브리드 창
창 함수는 다른 창문의 승법 또는 가법 조합으로도 구성되었다.
바틀렛-한 창
플랑크-베셀 창
§ Planck-taper 창과 수정된 Besel 함수의 관점에서 정의된 카이저 창을 곱한 창. 이 하이브리드 윈도우 기능은 플랑크 테이퍼 윈도우의 최고 측면 로브 수준을 낮추면서도 좋은 점증상 붕괴를 활용하기 위해 도입되었다.[79] 플랑크 테이퍼의 ε과 카이저 윈도우의 α인 두 개의 튜닝 가능한 파라미터를 가지므로 주어진 신호의 요건에 맞게 조정할 수 있다.
한-푸아송 창
( 의 경우 푸리에 변환이 주엽에서 영원히 떨어진다는 의미에서, 측면 로브가 없는 푸아송 창에 곱한 것이다. 따라서 뉴턴의 방법처럼 힐 클라이밍 알고리즘에 사용될 수 있다.[80] Hann-Poisson 창은 다음과 같이 정의된다.
여기서 α는 지수 기울기를 제어하는 매개변수다.
기타 창
일반화 적응 다항식(GAP) 창
GAP 창은[81] 순서 의 대칭적인 다항식 확장을 기반으로 한 조정 가능한 창 기능 계열로 도처에서 연속적으로 파생되는 형태로 지속되고 있다. 적절한 확장계수와 확장순서의 집합으로 GAP 창은 알려진 모든 윈도우 기능을 모방할 수 있으며, 그들의 스펙트럼 속성을 정확하게 재현한다.
여기서 은는) { 시퀀스의 표준 편차입니다.
또한 특정 알려진 윈도우 기능을 모방한 확장 계수 집합으로 시작하여 GAP 창을 최소화 절차에 의해 최적화하여 주엽 폭, 측엽 감쇠, 측엽 등 하나 이상의 스펙트럼 특성을 개선하는 새로운 계수 집합을 얻을 수 있다. 낙차율[83] 따라서 GAP 창 기능은 특정 용도에 따라 설계된 스펙트럼 속성으로 개발될 수 있다.
란초스창
- Lanczos resampling에 사용됨
- Lanczos 창의 경우 ) 은(는) ( )/ x x x로 정의된다.
- sinc 창이라고도 하며, 그 이유는 다음과 같다. 정상화된 동기 함수의 주엽이다.
창 비교
응용 프로그램에 적합한 창 함수를 선택할 때 이 비교 그래프가 유용할 수 있다. 길이 N의 창을 데이터에 적용하고 길이 N의 변환을 계산할 때 주파수 축은 FFT "빈"의 단위를 갖는다. 예를 들어 주파수 ½ "bin"(세 번째 눈금 표시)에서의 값은 주파수 k + ½에서 사인파 신호에 대해 빈 k 및 k + 1로 측정되는 응답이다. 신호 주파수가 빈의 정수일 때 발생하는 최대 가능 응답에 상대적이다. 빈도 ½에서의 값은 윈도우의 최대 가리비 손실이라고 하는데, 이것은 윈도우를 비교하는 데 사용되는 하나의 메트릭이다. 직사각형의 창은 그 측정기준에 있어서 다른 것들보다 눈에 띄게 나쁘다.
다른 지표는 주엽의 폭과 사이드로브의 피크 레벨로, 각각 비교 가능한 강도 신호와 이질적인 강도 신호를 해결할 수 있는 능력을 결정한다. 직사각형 창(예: 직사각형 창)은 전자를 위한 최선의 선택이며 후자를 위한 최악의 선택이다. 그래프에서 볼 수 없는 것은 직사각형 창이 가장 높은 소음 대역폭을 가지고 있기 때문에 그렇지 않은 경우 백색 소음 환경에서 낮은 수준의 사인파(syngoid)를 검출하기에 적합하다는 것이다. 무패딩과 주파수 변환과 같은 보간 기술은 그것의 잠재적 가리비 손실을 완화하기 위해 이용할 수 있다.
겹치는 창
변환할 데이터 세트의 길이가 원하는 주파수 분해능을 제공하기 위해 필요한 것보다 클 경우, 이를 더 작은 세트로 세분화하여 개별적으로 윈도우를 설정하는 것이 일반적인 관례다. 창 가장자리의 "손실"을 완화하기 위해 개별 세트가 시간에 겹칠 수 있다. 전력 스펙트럼 분석의 Welch 방법과 수정된 이산 코사인 변환을 참조한다.
2차원 창
이미지 푸리에 변환에서 원하지 않는 높은 빈도를 줄이기 위해 이미지 처리에 2차원 윈도우가 일반적으로 사용된다.[84] 그것들은 두 가지 형태 중 하나로 1차원 창문으로 만들어질 수 있다.[85] 분리 가능한 인 W( , )= w( ) ( ) 은 계산하기에 사소한 것이다. The radial form, , which involves the radius , is isotropic, independent on the orientation of the coordinate axes. 가우스 함수만이 분리가능성과 등방성 둘 다이다.[86] 다른 모든 창 함수의 분리 가능한 형태는 좌표 축의 선택에 따라 달라지는 코너를 가지고 있다. 2차원 창 기능의 동위원소/동위원소 로피는 2차원 푸리에 변환에 의해 공유된다. 분리형 및 방사형 형태의 차이는 직사각형 대 원형 개구부로부터의 회절의 결과와 유사하며, 이는 각각 두 개의 sinc 함수 대 a airy 함수의 곱으로 볼 수 있다.
참고 항목
메모들
- ^ 수학적으로 전달함수 H의 노이즈 등가 대역폭은 H와 동일한 피크 게인을 갖는 이상적인 직사각형 필터의 대역폭으로, 화이트 노이즈 입력으로 동일한 전력을 전달한다. 주파수 f 단위(예: 헤르츠)에서 다음과 같이 주어진다.
- ^ 잘림 현상이 스펙트럼 누설에 미치는 영향의 예는 그림 가우스 창이다. DTFT 주기8로 표시된 그래프는 주기적 DFT-짝수(두 파란색 모두)로 표시된 잘린 창의 DTFT이다. DTFT 대칭9라는 녹색 그래프는 대칭이 복원된 동일한 창에 해당한다. DFT8 주기적 합산으로 표시된 DTFT 샘플은 주기적 합계를 사용하여 파란색 그래프와 동일한 주파수에서 샘플링하는 예다.
- ^ 때로는 창과 창문이 없는(직사각형 창으로 된) DFT가 모두 필요하다.
- ^ 예를 들어 그림 DFT-짝수 Hann 창과 Hann( 'periodic')에서 생성된 시퀀스의 {\N} -길이 DFT가 0이 아닌 세 개의 값만 가지고 있음을 나타내는 DFT-짝수 Han 창을 참조하십시오. 다른 모든 샘플은 DTFT의 제로 크로싱과 일치한다.
- ^ 일부 저자들은 그들의 주의를 이 중요한 부분집합과 짝수 N 값으로 제한한다.[9][13] 그러나 창 계수 공식은 여전히 여기에 제시된 것이다.
- ^ 이 공식은 MATLAB tukeywin에서 코사인 함수를 단순화하고 r=α와 x=n/N을 대체함으로써 확인할 수 있다.
- ^ 해리스 1978(p 67, eq 38)은 다음과 같은 두 가지 오류를 가지고 있는 것으로 보인다. (1) 코사인함수의 분자에 있는 뺄셈 연산자가 추가되어야 한다. (2) 분모는 2의 가상 인자를 포함한다. 또한 그림 30은 위키백과 공식으로 α=0.25에 해당하지만 해리스 공식으로 0.75에 해당한다. 그림 32도 마찬가지로 라벨이 잘못 표시되어 있다.
- ^ 카이저 창은 종종 β에 의해 파라메트리되는데, 여기서 β = βα이다.[63][64] [65][66][60][67][19]: p. 474 단지 α의 대체 사용은 DPSS 창문과의 비교를 용이하게 한다.[68]
페이지 인용구
참조
- ^ Weisstein, Eric W. (2003). CRC Concise Encyclopedia of Mathematics. CRC Press. ISBN 978-1-58488-347-0.
- ^ Roads, Curtis (2002). Microsound. MIT Press. ISBN 978-0-262-18215-7.
- ^ Cattani, Carlo; Rushchitsky, Jeremiah (2007). Wavelet and Wave Analysis As Applied to Materials With Micro Or Nanostructure. World Scientific. ISBN 978-981-270-784-0.
- ^ "Overlap-Add (OLA) STFT Processing Spectral Audio Signal Processing". www.dsprelated.com. Retrieved 2016-08-07.
The window is applied twice: once before the FFT (the "analysis window") and secondly after the inverse FFT prior to reconstruction by overlap-add (the so-called "synthesis window"). ... More generally, any positive COLA window can be split into an analysis and synthesis window pair by taking its square root.
- ^ a b c d Nuttall, Albert H. (Feb 1981). "Some Windows with Very Good Sidelobe Behavior". IEEE Transactions on Acoustics, Speech, and Signal Processing. 29 (1): 84–91. doi:10.1109/TASSP.1981.1163506. 해리스의 논문을 확장하여, 주요 메트릭 비교와 함께 당시 알려진 모든 윈도우 기능을 다룬다.
- ^ Carlson, A. Bruce (1986). Communication Systems: An Introduction to Signals and Noise in Electrical Communication. McGraw-Hill. ISBN 978-0-07-009960-9.
- ^ a b "Hann (Hanning) window - MATLAB hann". www.mathworks.com. Retrieved 2020-02-12.
- ^ "Window Function". www.mathworks.com. Retrieved 2019-04-14.
- ^ a b c d e f g h i j k l m Harris, Fredric J. (Jan 1978). "On the use of Windows for Harmonic Analysis with the Discrete Fourier Transform" (PDF). Proceedings of the IEEE. 66 (1): 51–83. Bibcode:1978IEEEP..66...51H. CiteSeerX 10.1.1.649.9880. doi:10.1109/PROC.1978.10837. S2CID 426548. 해리스가 FFT 창문에 대한 1978년 기본 논문은 많은 창을 명시하고 그것들을 비교하는 데 사용된 주요 측정 기준을 소개했다.
- ^ Robertson, Neil (18 December 2018). "Evaluate Window Functions for the Discrete Fourier Transform". DSPRelated.com. The Related Media Group. Retrieved 9 August 2020. 2020년 2월 22일 개정.
- ^ "Matlab for the Hann Window". ccrma.stanford.edu. Retrieved 2020-09-01.
- ^ Rohling, H.; Schuermann, J. (March 1983). "Discrete time window functions with arbitrarily low sidelobe level". Signal Processing. Forschungsinstitut Ulm, Sedanstr, Germany: AEG-Telefunken. 5 (2): 127–138. doi:10.1016/0165-1684(83)90019-1. Retrieved 8 August 2020.
It can be shown, that the DFT-even sampling technique as proposed by Harris is not the most suitable one.
- ^ a b c d Heinzel, G;Rüdiger A.;실링, R(2002년).그 이산 푸리에 변환(DFT)에 의해 윈도우 함수들의 포괄적인 목록과 몇몇 새로운 상고 머리 창문(기술 보고서)을 포함한 스펙트럼이 이동하였고 스펙트럼 밀도 추정.막스 플랑크(평균 탄착 중심점)für Gravitationsphysik/레이저 간섭계에 의한 관측&중력 파동의 천문학.395068.0.2013-02-10 Retrieved.또한https://pure.mpg.de/rest/items/item_152164_1/component/file_152163/content에서 이용할 수
- ^ Lyons, Richard (1 June 1998). "Windowing Functions Improve FFT Results". EDN. Sunnyvale, CA: TRW. Retrieved 8 August 2020.
- ^ Fulton, Trevor (4 March 2008). "DP Numeric Transform Toolbox". herschel.esac.esa.int. Herschel Data Processing. Retrieved 8 August 2020.
- ^ Poularikas, A.D. (1999). "7.3.1". In Poularikas, Alexander D. (ed.). The Handbook of Formulas and Tables for Signal Processing (PDF). Boca Raton: CRC Press LLC. ISBN 0849385792. Retrieved 8 August 2020.
Windows are even (about the origin) sequences with an odd number of points. The right-most point of the window will be discarded.
- ^ Puckette, Miller (30 December 2006). "Fourier analysis of non-periodic signals". msp.ucsd.edu. UC San Diego. Retrieved 9 August 2020.
- ^ 미국 특허 6898235, 칼린, 조, 콜린스Terry & Hays, Peter 등, 1999-12-10년에 출판된 "하이퍼채널화를 이용한 광대역 통신 차단 및 방향 찾기 장치"는 https://patentimages.storage.googleapis.com/4d/39/2a/cec2ae6f33c1e7/US6898235.pdf에서도 2005-05-24를 발행할 수 있다.
- ^ a b Oppenheim, Alan V.; Schafer, Ronald W.; Buck, John R. (1999). "7.2". Discrete-time signal processing (2nd ed.). Upper Saddle River, N.J.: Prentice Hall. pp. 465–478. ISBN 0-13-754920-2. url=https://d1.amobbs.com/bbs_upload782111/files_24/ourdev_523225.pdf
- ^ "FIR Filters by Windowing – The Lab Book Pages". www.labbookpages.co.uk. Retrieved 2016-04-13.
- ^ "Mastering Windows" (PDF). www.cg.tuwien.ac.at. Retrieved 2020-02-12.
- ^ "The Fundamentals of Signal Analysis Application Note 243" (PDF). hpmemoryproject.org. Retrieved 10 April 2018.
- ^ "Zero Phase Filters". ccrma.stanford.edu. Retrieved 2020-02-12.
- ^ Rorabaugh, C.Britton (October 1998). DSP Primer. Primer series. McGraw-Hill Professional. p. 196. ISBN 978-0070540040.
- ^ Toraichi, K.; Kamada, M.; Itahashi, S.; Mori, R. (1989). "Window functions represented by B-spline functions". IEEE Transactions on Acoustics, Speech, and Signal Processing. 37: 145–147. doi:10.1109/29.17517.
- ^ "Bartlett Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ Tukey, J.W. (1967). "An introduction to the calculations of numerical spectrum analysis". Spectral Analysis of Time Series: 25–46.
- ^ "Triangular window – MATLAB triang". www.mathworks.com. Retrieved 2016-04-13.
- ^ a b Welch, P. (1967). "The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms". IEEE Transactions on Audio and Electroacoustics. 15 (2): 70–73. Bibcode:1967ITAE...15...70W. doi:10.1109/TAU.1967.1161901.
- ^ Bosi, Marina; Goldberg, Richard E. (2003). "Time to Frequency Mapping Part II: The MDCT". Introduction to Digital Audio Coding and Standards. The Springer International Series in Engineering and Computer Science. Vol. 721. Boston, MA: Springer US. p. 106. doi:10.1007/978-1-4615-0327-9. ISBN 978-1-4615-0327-9.
- ^ Kido, Ken'iti; Suzuki, Hideo; Ono, Takahiko; Fukushima, Manabu (1998). "Deformation of impulse response estimates by time window in cross spectral technique". Journal of the Acoustical Society of Japan (E). 19 (5): 349–361. doi:10.1250/ast.19.349.
- ^ Landisman, M.; Dziewonski, A.; Satô, Y. (1969-05-01). "Recent Improvements in the Analysis of Surface Wave Observations". Geophysical Journal International. 17 (4): 369–403. Bibcode:1969GeoJ...17..369L. doi:10.1111/j.1365-246X.1969.tb00246.x.
- ^ "Bohman window – R2019B". www.mathworks.com. Retrieved 2020-02-12.
- ^ "Power-of-Cosine Window Family". ccrma.stanford.edu. Retrieved 10 April 2018.
- ^ "Hann or Hanning or Raised Cosine". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ Enochson, Loren D.; Otnes, Robert K. (1968). Programming and Analysis for Digital Time Series Data. U.S. Dept. of Defense, Shock and Vibration Info. Center. p. 142.
- ^ a b c "Hamming Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ "A digital quadrature amplitude modulation (QAM) Radio: Building a better radio" (PDF). users.wpi.edu. p. 28. Retrieved 2020-02-12.
- ^ "Bits to Symbols to Signals and back again" (PDF). users.wpi.edu. p. 7. Retrieved 2020-02-12.
- ^ Johnson, C.Richard, Jr; Sethares, William A.; Klein, Andrew G. (2011-08-18). "11". Software Receiver Design. Cambridge University Press. ISBN 978-1139501453. 또한 https://cnx.org/contents/QsVBJjB4@3.1:6R_zzDY@4/Pulse-Shaping-and-Receive-Filtering
- ^ Weisstein, Eric W. "Blackman Function". mathworld.wolfram.com. Retrieved 2016-04-13.
- ^ "Characteristics of Different Smoothing Windows - NI LabVIEW 8.6 Help". zone.ni.com. Retrieved 2020-02-13.
- ^ Blackman, R.B.; Tukey, J.W. (1959-01-01). The Measurement of Power Spectra from the Point of View of Communications Engineering. Dover Publications. p. 99. ISBN 9780486605074.
- ^ "Blackman-Harris Window Family". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ "Three-Term Blackman-Harris Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ a b Smith, Steven W. (2011). The Scientist and Engineer's Guide to Digital Signal Processing. San Diego, California, USA: California Technical Publishing. Retrieved 2013-02-14.
- ^ Rife, David C.; Vincent, G.A. (1970), "Use of the discrete Fourier transform in the measurement of frequencies and levels of tones", Bell Syst. Tech. J., 49 (2): 197–228, doi:10.1002/j.1538-7305.1970.tb01766.x
- ^ a b Andria, Gregorio; Savino, Mario; Trotta, Amerigo (1989), "Windows and interpolation algorithms to improve electrical measurement accuracy", IEEE Transactions on Instrumentation and Measurement, 38 (4): 856–863, doi:10.1109/19.31004
- ^ Schoukens, Joannes; Pintelon, Rik; Van Hamme, Hugo (1992), "The interpolated fast Fourier transform: a comparative study", IEEE Transactions on Instrumentation and Measurement, 41 (2): 226–232, doi:10.1109/19.137352
- ^ a b "Matlab for the Gaussian Window". ccrma.stanford.edu. Retrieved 2016-04-13.
Note that, on a dB scale, Gaussians are quadratic. This means that parabolic interpolation of a sampled Gaussian transform is exact. ... quadratic interpolation of spectral peaks may be more accurate on a log-magnitude scale (e.g., dB) than on a linear magnitude scale
- ^ "Gaussian Window and Transform". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ "Quadratic Interpolation of Spectral Peaks". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ a b c Starosielec, S.; Hägele, D. (2014). "Discrete-time windows with minimal RMS bandwidth for given RMS temporal width". Signal Processing. 102: 240–246. doi:10.1016/j.sigpro.2014.03.033.
- ^ Chakraborty, Debejyo; Kovvali, Narayan (2013). "Generalized normal window for digital signal processing". 2013 IEEE International Conference on Acoustics, Speech and Signal Processing. pp. 6083–6087. doi:10.1109/ICASSP.2013.6638833. ISBN 978-1-4799-0356-6. S2CID 11779529.
- ^ Diethorn, E.J. (1994). "The generalized exponential time-frequency distribution". IEEE Transactions on Signal Processing. 42 (5): 1028–1037. Bibcode:1994ITSP...42.1028D. doi:10.1109/78.295214.
- ^ Bloomfield, P. (2000). Fourier Analysis of Time Series: An Introduction. New York: Wiley-Interscience.
- ^ Tu, Loring W. (2008). "Bump Functions and Partitions of Unity". An Introduction to Manifolds. Universitext. New York: Springer. pp. 127–134. doi:10.1007/978-0-387-48101-2_13. ISBN 978-0-387-48098-5.
- ^ McKechan, D.J.A.; Robinson, C.; Sathyaprakash, B.S. (21 April 2010). "A tapering window for time-domain templates and simulated signals in the detection of gravitational waves from coalescing compact binaries". Classical and Quantum Gravity. 27 (8): 084020. arXiv:1003.2939. Bibcode:2010CQGra..27h4020M. doi:10.1088/0264-9381/27/8/084020. S2CID 21488253.
- ^ "Slepian or DPSS Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ a b Smith, J.O. (2011). "Kaiser and DPSS Windows Compared". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ Kaiser, James F.; Kuo, Franklin F. (1966). System Analysis by Digital Computer. John Wiley and Sons. pp. 232–235.
This family of window functions was "discovered" by Kaiser in 1962 following a discussion with B. F. Logan of the Bell Telephone Laboratories. ... Another valuable property of this family ... is that they also approximate closely the prolate spheroidal wave functions of order zero.
- ^ Kaiser, James F. (Nov 1964). "A family of window functions having nearly ideal properties". Unpublished Memorandum.
- ^ Rabiner, Lawrence R.; Gold, Bernard (1975). "3.11". Theory and application of digital signal processing. Englewood Cliffs, N.J.: Prentice-Hall. p. 94. ISBN 0-13-914101-4.
- ^ Crochiere, R.E.; Rabiner, L.R. (1983). "4.3.1". Multirate Digital Signal Processing. Englewood Cliffs, NJ: Prentice-Hall. p. 144. ISBN 0136051626.
- ^ Lin, Yuan-Pei; Vaidyanathan, P.P. (June 1998). "A Kaiser Window Approach for the Design of Prototype Filters of Cosine Modulated Filterbanks" (PDF). IEEE Signal Processing Letters. 5 (6): 132–134. Bibcode:1998ISPL....5..132L. doi:10.1109/97.681427. S2CID 18159105. Retrieved 2017-03-16.
- ^ Smith, J.O. (2011). "Kaiser Window". ccrma.stanford.edu. Retrieved 2019-03-20.
Sometimes the Kaiser window is parametrized by α, where β = πα.
- ^ "Kaiser Window, R2020a". www.mathworks.com. Mathworks. Retrieved 9 April 2020.
- ^ "Kaiser Window". www.dsprelated.com. Retrieved 2020-04-08.
The following Matlab comparison of the DPSS and Kaiser windows illustrates the interpretation of α as the bin number of the edge of the critically sampled window main lobe.
- ^ Kaiser, James F.; Schafer, Ronald W. (1980). "On the use of the I0-sinh window for spectrum analysis". IEEE Transactions on Acoustics, Speech, and Signal Processing. 28: 105–107. doi:10.1109/TASSP.1980.1163349.
- ^ a b c "Dolph-Chebyshev Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ "Dolph-Chebyshev Window Definition". ccrma.stanford.edu. Retrieved 2019-03-05.
- ^ a b c Kabal, Peter (2009). "Time Windows for Linear Prediction of Speech" (PDF). Technical Report, Dept. Elec. & Comp. Eng., McGill University (2a): 31. Retrieved 2 February 2014.
- ^ Streit, Roy (1984). "A two-parameter family of weights for nonrecursive digital filters and antennas". Transactions of ASSP. 32: 108–118. doi:10.1109/tassp.1984.1164275.
- ^ a b c d Deczky, Andrew (2001). "Unispherical Windows". ISCAS 2001. The 2001 IEEE International Symposium on Circuits and Systems (Cat. No.01CH37196). Vol. 2. pp. 85–88. doi:10.1109/iscas.2001.921012. ISBN 978-0-7803-6685-5. S2CID 38275201.
- ^ Bergen, S.W.A.; Antoniou, A. (2004). "Design of Ultraspherical Window Functions with Prescribed Spectral Characteristics". EURASIP Journal on Applied Signal Processing. 2004 (13): 2053–2065. Bibcode:2004EJASP2004...63B. doi:10.1155/S1110865704403114.
- ^ 버겐, 스튜어트 A. (2005년) "Design of the Ultraspherical Window Function and Its Applications" (PDF). 논문, 빅토리아 대학
- ^ Smith, Julius O. III (2011-04-23). "Poisson Window". ccrma.stanford.edu. Retrieved 2020-02-12.
- ^ Gade, Svend; Herlufsen, Henrik (1987). "Technical Review No 3-1987: Windows to FFT analysis (Part I)" (PDF). Brüel & Kjær. Retrieved 2011-11-22.
- ^ Berry, C.P.L.; Gair, J.R. (12 December 2012). "Observing the Galaxy's massive black hole with gravitational wave bursts". Monthly Notices of the Royal Astronomical Society. 429 (1): 589–612. arXiv:1210.2778. Bibcode:2013MNRAS.429..589B. doi:10.1093/mnras/sts360. S2CID 118944979.
- ^ "Hann-Poisson Window". ccrma.stanford.edu. Retrieved 2016-04-13.
- ^ Justo, J. F.; Beccaro, W. (2020-10-26). "Generalized Adaptive Polynomial Window Function". IEEE Access. 8: 187584–187589. doi:10.1109/ACCESS.2020.3030903. S2CID 225050036. Retrieved 2020-10-31.
- ^ Wesley Beccaro (2020-10-31), "Generalized Adaptive Polynomial Window Function", mathworks.com, retrieved 2020-11-02
- ^ "Generalized Adaptive Polynomial Window Function". www.mathworks.com. Retrieved 2020-12-12.
- ^ R. Hovden, Y. Jiang, H. Xin, L.F. Kourkoutis (2015). "Periodic Artifact Reduction in Fourier Transforms of Full Field Atomic Resolution Images". Microscopy and Microanalysis. 21 (2): 436–441. Bibcode:2015MiMic..21..436H. doi:10.1017/S1431927614014639. PMID 25597865.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ Bernstein, Matt A.; King, Kevin Franklin; Zhou, Xiaohong Joe (2004). Handbook of MRI Pulse Sequences. London: Elsevier Academic Press. pp. 495–499. ISBN 0120928612.
- ^ Awad, A.I.; Baba, K. (2011). "An Application for Singular Point Location in Fingerprint Classification". Digital Information Processing and Communications. Communications in Computer and Information Science. Vol. 188. p. 262. doi:10.1007/978-3-642-22389-1_24. ISBN 978-3-642-22388-4.
추가 읽기
- Harris, Frederic J. (September 1976). "Windows, Harmonic Analysis, and the Discrete Fourier Transform" (PDF). apps.dtic.mil. Naval Undersea Center, San Diego. Retrieved 2019-04-08.
- Albrecht, Hans-Helge (2012). Tailored minimum sidelobe and minimum sidelobe cosine-sum windows. Version 1.0. Vol. ISBN 978-3-86918-281-0 ). editor: Physikalisch-Technische Bundesanstalt. Physikalisch-Technische Bundesanstalt. doi:10.7795/110.20121022aa. ISBN 978-3-86918-281-0.
- Bergen, S.W.A.; Antoniou, A. (2005). "Design of Nonrecursive Digital Filters Using the Ultraspherical Window Function". EURASIP Journal on Applied Signal Processing. 2005 (12): 1910–1922. Bibcode:2005EJASP2005...44B. doi:10.1155/ASP.2005.1910.
- Prabhu, K. M. M. (2014). Window Functions and Their Applications in Signal Processing. Boca Raton, FL: CRC Press. ISBN 978-1-4665-1583-3.
- 미국 특허 7065150, Park, Young-Seo, 2003년 발행, 2006년 발행된 "루트 상승 코사인 직교 주파수 분할 다중화(RRC OFDM) 생성 시스템 및 방법"
외부 링크
 Wikimedia Commons의 창 기능과 관련된 미디어
Wikimedia Commons의 창 기능과 관련된 미디어- LabView 도움말, 스무딩 필터의 특성, http://zone.ni.com/reference/en-XX/help/371361B-01/lvanlsconcepts/char_smoothing_windows/
- Cosine-sum 창 기능 생성 및 속성, http://electronicsart.weebly.com/fftwindows.html
- 온라인 인터랙티브 FFT, Windows, 해상도 및 누출 시뮬레이션 RISEC 라이브러리 & 툴



![{\displaystyle wh[N]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13698c9f64b16adf6d590131560e4df88ff129a9)



![{\displaystyle w[N]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdf14952660bd2a67ffd5b3a1e8e63a7eeb841f9) (는)
(는) ![{\displaystyle w[0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10b66d5ea341ae37d4ba6529d614a75434f91cf2)


 ,
,
![{\displaystyle x\in [-N/2,N/2],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0377d29e5715ebdd13819c1cc07c4638a0156afd)
![{\displaystyle \{w[n]=w_{0}(n-N/2),\quad 0\leq n\leq N\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f28eb10c2426fe0deb507ce933eb6b5df2c020e)

![{\displaystyle \{w[n],\quad 0\leq n\leq N-1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f506d61ded38a4f9d8ecd59004fbf34e793d81f3) (는) 길이가
(는) 길이가 
![{\displaystyle w[n]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f071fdd6a0a02d6d9dc3c1325d88a6dda6a92781)
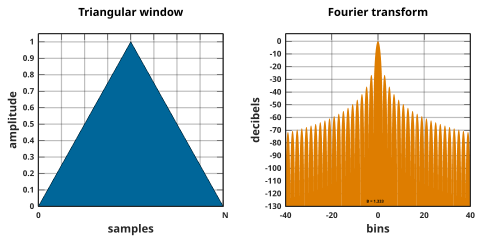
![{\displaystyle w[n]=1-\left|{\frac {n-{\frac {N}{2}}}{\frac {L}{2}}}\right|,\quad 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/884ef77423e593a74ebf40ec3eaa0c8f00ca5102)


![{\displaystyle w[n]=\ w_{0}\left(n-{\tfrac {N}{2}}\right),\ 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfa5797bd28cc542de9f224e4b9c7c0c37bff91a)

![{\displaystyle w[n]=1-\left({\frac {n-{\frac {N}{2}}}{\frac {N}{2}}}\right)^{2},\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa3a944c6a5c2051217a53dd60a9693dd76c98a9)

![{\displaystyle w[n]=\sin \left({\frac {\pi n}{N}}\right)=\cos \left({\frac {\pi n}{N}}-{\frac {\pi }{2}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bc2af9f7febc105f1184bd114a1484bf16cf7325)

![{\displaystyle w[n]=\sin ^{\alpha }\left({\frac {\pi n}{N}}\right)=\cos ^{\alpha }\left({\frac {\pi n}{N}}-{\frac {\pi }{2}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b81af4c85e4b5e6909b3dfb7fef170a42a02f7e)
![{\displaystyle w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)-a_{3}\cos \left({\frac {6\pi n}{N}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55aa618bd5010d83e5df4ae06fbb3abd509f12fd)

![{\displaystyle w[n]=\sum _{k=0}^{K}(-1)^{k}a_{k}\;\cos \left({\frac {2\pi kn}{N}}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e597f0587d0c29feaf791fef475cf419be2987c9)


![{\displaystyle w[n]=a_{0}-\underbrace {(1-a_{0})} _{a_{1}}\cdot \cos \left({\tfrac {2\pi n}{N}}\right),\quad 0\leq n\leq N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72b8f8c3192b06191db2bb7ad9247eeba6a6cb70)
![{\displaystyle {\begin{aligned}w_{0}(n)\ &=w\left[n+{\tfrac {N}{2}}\right]\\&=a_{0}+a_{1}\cdot \cos \left({\tfrac {2\pi n}{N}}\right),\quad -{\tfrac {N}{2}}\leq n\leq {\tfrac {N}{2}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a04d79e8c4de591b5badfd2864ebe7522c17b1ad)
 :
: ![{\displaystyle w[n]=0.5\;\left[1-\cos \left({\frac {2\pi n}{N}}\right)\right]=\sin ^{2}\left({\frac {\pi n}{N}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd8d3e844a1443d7bedd57240588cf19fcd28af1)

 약 0.54로 설정하거나, 보다 정확하게 25/46으로 설정하면
약 0.54로 설정하거나, 보다 정확하게 25/46으로 설정하면 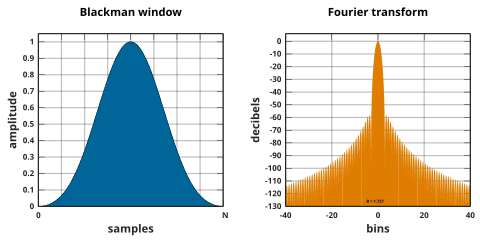
![{\displaystyle w[n]=a_{0}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e1a6c47fc77da0b81229c3234068706a6ca8e6a)








![{\displaystyle {\begin{aligned}w[n]=a_{0}&{}-a_{1}\cos \left({\frac {2\pi n}{N}}\right)+a_{2}\cos \left({\frac {4\pi n}{N}}\right)\\&{}-a_{3}\cos \left({\frac {6\pi n}{N}}\right)+a_{4}\cos \left({\frac {8\pi n}{N}}\right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e117d087bf8d6345fb6ea8ffc7b5aa7f6faae4a)


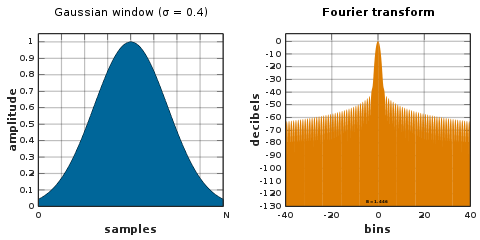
![{\displaystyle w[n]=\exp \left(-{\frac {1}{2}}\left({\frac {n-N/2}{\sigma N/2}}\right)^{2}\right),\quad 0\leq n\leq N.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e201c829f6aabf4339fc0a1929367d5613dfe290)

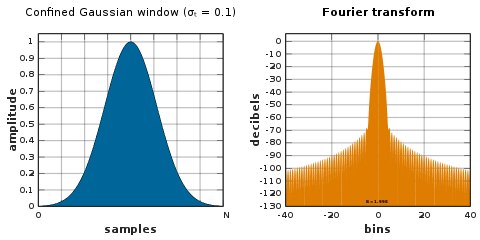

![{\displaystyle w[n]=G(n)-{\frac {G(-{\tfrac {1}{2}})[G(n+L)+G(n-L)]}{G(-{\tfrac {1}{2}}+L)+G(-{\tfrac {1}{2}}-L)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3094fa9469d1e65bfdb6a4e31cdafd037a8822ec)
 (는) 가우스 함수:
(는) 가우스 함수: 
![{\displaystyle w[n,p]=\exp \left(-\left({\frac {n-N/2}{\sigma N/2}}\right)^{p}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/704a7de7c2a67fc8a24a140a151491bd7362698c)




![{\displaystyle \left.{\begin{array}{lll}w[n]={\frac {1}{2}}\left[1-\cos \left({\frac {2\pi n}{\alpha N}}\right)\right],\quad &0\leq n<{\frac {\alpha N}{2}}\\w[n]=1,\quad &{\frac {\alpha N}{2}}\leq n\leq {\frac {N}{2}}\\w[N-n]=w[n],\quad &0\leq n\leq {\frac {N}{2}}\end{array}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab34271ac62f34c531c4d6cc0b8ffd2e9793623a)


![{\displaystyle \left.{\begin{array}{lll}w[0]=0,\\w[n]=\left(1+\exp \left({\frac {\varepsilon N}{n}}-{\frac {\varepsilon N}{\varepsilon N-n}}\right)\right)^{-1},\quad &1\leq n<\varepsilon N\\w[n]=1,\quad &\varepsilon N\leq n\leq {\frac {N}{2}}\\w[N-n]=w[n],\quad &0\leq n\leq {\frac {N}{2}}\end{array}}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f50bb4690593ab87a47ed71fec1945a3f95b9d0d)




![{\displaystyle w[n]={\frac {I_{0}\left(\pi \alpha {\sqrt {1-\left({\frac {2n}{N}}-1\right)^{2}}}\right)}{I_{0}(\pi \alpha )}},\quad 0\leq n\leq N}](https://wikimedia.org/api/rest_v1/media/math/render/svg/337ca65bf1465649348a8eb22356662c4188b092)

 첫 번째 종류의 0번째 순서 수정 Besel 함수다. 가변 파라미터
첫 번째 종류의 0번째 순서 수정 Besel 함수다. 가변 파라미터 


![{\displaystyle w_{0}[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0d68356ad0cc45bf520fbe5be3266aa7c431cd8)
![{\displaystyle W_{0}[k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af1b9baa4526ac8ec5f39c3cd63782248015037f)





![{\displaystyle w[n]=w_{0}\left(n-{\frac {N}{2}}\right),\quad 0\leq n\leq N,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3af173b60d19716e14882dabdec080868fa3e0ae)
![{\displaystyle {\begin{aligned}w_{0}\left(n-{\frac {N}{2}}\right)={\frac {1}{N+1}}\sum _{k=0}^{N}W_{0}(k)\cdot e^{\frac {i2\pi k(n-N/2)}{N+1}}={\frac {1}{N+1}}\sum _{k=0}^{N}\left[\left(-e^{\frac {i\pi }{N+1}}\right)^{k}\cdot W_{0}(k)\right]e^{\frac {i2\pi kn}{N+1}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24f3590133d3da32b13aa211153542e96d14a46e)


![{\displaystyle w[n]={\frac {1}{N+1}}\left[C_{N}^{\mu }(x_{0})+\sum _{k=1}^{\frac {N}{2}}C_{N}^{\mu }\left(x_{0}\cos {\frac {k\pi }{N+1}}\right)\cos {\frac {2n\pi k}{N+1}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe5e8dc43d2c5edbe601e3abf542a177689f4276)
 (는) N의
(는) N의  (
(




![{\displaystyle w[n]=e^{-\left|n-{\frac {N}{2}}\right|{\frac {1}{\tau }}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/141d1630d759c1ebf5120671e36f86a6117f259c)

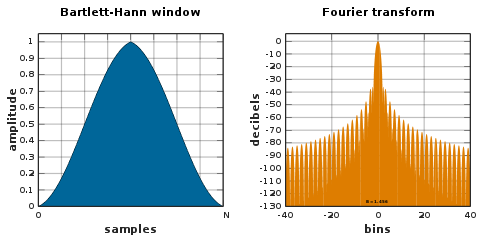
![{\displaystyle w[n]=a_{0}-a_{1}\left|{\frac {n}{N}}-{\frac {1}{2}}\right|-a_{2}\cos \left({\frac {2\pi n}{N}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e64d33f0c717a2b40af2ed16c9fff5f58d95b937)




![{\displaystyle w[n]={\frac {1}{2}}\left(1-\cos \left({\frac {2\pi n}{N}}\right)\right)e^{\frac {-\alpha \left|N-2n\right|}{N}}\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e7d44df8e90604b099629079cb1ed07faa045a3)


![{\displaystyle w_{0}[n]=a_{0}+\sum _{k=1}^{K}a_{2k}\left({\frac {n}{\sigma }}\right)^{2k},\quad -{\frac {N}{2}}\leq n\leq {\frac {N}{2}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0985efd235d3dcfbd7c9a2631aa173cd5c2d4cdf)




![{\displaystyle w[n]=\operatorname {sinc} \left({\frac {2n}{N}}-1\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/380ec565d5a93c55eb9d1109065556115b5c0f99)










