라브 그래프

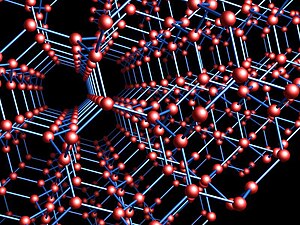
기하학과 결정학에서 라베스 그래프는 3차원 유클리드 공간의 점과 선분의 무한하고 매우 대칭적인 체계로 주기적인 그래프를 형성합니다.길이가 같은 세그먼트 3개가 각 지점에서 120° 각도로 만나며 모든 사이클은 10개 이상의 세그먼트를 사용합니다.이것은 기본 영역의 부피에 비해 가능한 가장 짧은 3배 주기 그래프입니다.라베스 그래프의 한 배열은 정수 격자에 있는 점들 중 8개의 점들 중 1개를 점으로 사용하고, 가장 가까운 이웃인 이 점들의 모든 쌍을 거리 $2{\displaystyle \sqrt{\mathrm{}}}$ ${\$에서 연결합니다$.$ 또한 기하학과 분리되어 추상적인 무방향 그래프로 정의될 수 있습니다.완전한 그래프를 4개의 꼭짓점 위에 덮은 그래프

H. S. M. Coxeter (1955)는 이 그래프를 1932년에 처음으로 결정 구조라고 쓴 Fritz Laves의 이름을 따서 이름 지었습니다.^[1][2]그것은 또한 K 크리스탈₄,^[3] (10,3)-네트워크,^[4] 다이아몬드 트윈,^[5] 트라이아몬드,^[6][7] 그리고 srs 네트라고도 불립니다.^[8]그래프의 각 꼭짓점에 가장 가까운 공간 영역은 공간을 타일링하는 합동 17변 다면체입니다.그 가장자리는 공간의 각 정수점에서 만나는 6개의 정사각형이 있는 표면인 정규 스큐 다면체의 대각선 위에 놓여 있습니다.

몇몇 결정성 화학물질들은 라베스 그래프의 형태로 구조를 알고 있거나 예측해 왔습니다.라브 그래프의 가장자리를 실린더로 두껍게 하면 관련된 최소 표면인 자이로이드가 생성됩니다. 자이로이드는 특정한 비누막 구조와 나비의 날개에서 물리적으로 나타납니다.

시공

정수 그리드로부터

Coxeter(1955)가 설명한 바와 같이, Laves 그래프의 정점은 3차원 정수 격자의 8개의 점 중 하나를 선택하여 가장 가까운 이웃 그래프를 형성함으로써 정의될 수 있습니다.구체적으로, 한 사람이 포인트를 선택합니다.

그리고 이 좌표들에 4의 배수를 더함으로써 형성된 다른 모든 점들.Laves 그래프의 가장자리는 유클리드 거리가 2개의 제곱근인 점들의 쌍을 연결하는데$,$ $이$는 각 쌍의 점들이 2개의 좌표에서 한 단위씩 다르고 세 번째 $좌표$에서 동일하기 때문입니다$.$모서리는 평평한 평면에서 각 꼭지점에서 120°각도로 마주칩니다.인접하지 않은 모든 정점 쌍은 서로 최소 $6{\displaystyle \sqrt{\mathrm{}}}$ ${\$만큼$$ 떨어져 있습니다.결과 기하 그래프의 가장자리는 꼭짓점당 6개의 정사각형 면이 있는 정규 스큐 다면체의 면 부분 집합의 대각선이므로, 라베스 그래프는 이 스큐 다면체에 포함됩니다.^[1]

정수 격자의 4개의 점들 중 하나의 더 큰 집합을 선택할 수 있으므로, 이 더 큰 집합의 ${\displaystyle \sqrt{\mathrm{}}}$2 {\$displaystyle${\$sqrt$ {2$$$}}$ 쌍의 그래프는 서로 단절된 라베스 그래프의 두 개의 거울-이미지 복사본을 형성하며, 다른 모든 점 $쌍$은 2 ${\$보다 더 멀리 떨어져 있습니다.^[9]

피복 그래프로서

추상 그래프로서, 라베스 그래프는 완전 그래프 ${\displaystyle {K4\mathrm{}}_{}}$ ${\$의 최대 아벨리안 피복 그래프로 구성될 수 있습니다$.$${\displaystyle {K4\mathrm{}}_{}}$ ${\$의 아벨리안 커버링 그래프가 된다는 것은 라베스 그래프의 꼭짓점이 다른 세 가지 색의 이웃을 가지고, 어떤 꼭짓점을 같은 색의 다른 꼭짓점으로 가져가려는 색 보존 대칭이 존재하는 4색일 수 있다는 것을$$ 의미합니다.정수 좌표가 있는 기하학적 형태의 라브 그래프의 경우, 이러한 대칭은 각 좌표에 짝수를 추가하는 변환입니다(추가적으로 세 좌표의 오프셋은 모두 일치하는 모듈로 4여야 함).두 번의 번역을 연속적으로 적용할 때, 순 번역은 그 순서와 무관합니다: 그들은 서로 출퇴근하여 아벨리안 그룹을 형성합니다.이 그룹의 번역 벡터는 3차원 격자를 형성합니다.마지막으로, 최대 아벨리안 피복 그래프가 된다는 것은 고차원 격자를 포함하는$$ ${\displaystyle {K4\mathrm{}}_{}}$ ${\$의 다른 피복 그래프가 없다는 것을 의미합니다.이 구조는 Laves 그래프의 대체 $이름$인 ${\displaystyle {K4\mathrm{}}_{}}$ ${\$ 결정을$$ 정당화합니다.^[10]

최대 아벨리안 피복 그래프는 임의의 유한 $그래프{\displaystyle }$ G ${\displaystyle$ G$}$로부터 구성될 수 있으며$,$ ${\displaystyle {K4\mathrm{}}_{}}$ ${\$에 적용되며$,$ 구성은 (추상) 라브 그래프를 생성하지만 동일한 기하학적 레이아웃을 제공하지 않습니다.$G{\displaystyle }$ ${\displaystyle G}$의 스패닝 트리를 선택하고$$${\displaystyle d}$을(를) 스패닝 트리에 없는 에지(이 경우 세 개의 비 트리 에지)의 개수라고 $하고{\displaystyle }$ 각 비 트리 에지에 대해$$ Z ${\displaystyle {}^{}}$ ${\$의 고유 단위 벡터를 선택합니다.${\displaystyle \mathrm{그런}}$ 다음 v ${\displaystyle v}$가 $G{\displaystyle }$ ${\displaystyle G}$의 정점이고 $w$ ${\displaystyle w}$가 $Z{\displaystyle {\mathbb{}}^{}}$ ${\$의 벡터가 되도록$$ 피복 그래프의 정점 집합을${\displaystyle }$고정합니다$.$ 각 쌍 및 $G{\displaystyle }$ ${\displ$}의$$ $v{\displaystyle }$ ${\displaystyle v}$에 인접한 각 에지 u ${\displaystyle v}$ ${\displaystyle uv}$에 대해$aystyle$ G$},$(v$,{\displaystyle w)}$ ${\displaystyle$ (v$,w)}$에서 (u$,{\displaystyle w}$±${\displaystyle }$$ϵ$) ${\displaystyle$ (u$,$$w\pm$ \$epsilon )}$까지의 간선을 만듭니다. 여기서 $ϵ$ ${\displaystyle$ \$epsilon$}이$($가) 신장 트리에 속하고, $그렇지$않으면 uv ${\displaystyle uv$}와$$연결된 기본 벡터입니다.가장자리가 지나는 방향에 따라 플러스 기호 또는 마이너스 기호가 선택되는 경우.결과 그래프는 선택한 신장 트리와는 독립적이며, 동일한 구성을 호몰로지를 사용하여 보다 추상적으로 해석할 수도 있습니다.^[11]

동일한 구성을 사용하여 평면의 육각 타일링은 3 모서리 쌍극자 그래프의 최대 아벨라인 피복 그래프이고, 다이아몬드 큐빅은 4 모서리 쌍극자의 최대 아벨라인 피복 그래프입니다.$d{\displaystyle }$ ${\displaystyle d}$ - 차원$$ 정수 격자(단위 길이 에지가 있는 그래프)는 하나의 정점과 $d{\displaystyle }$ ${\displaystyle d}$개의 자기 루프가 있는$$ 그래프의 최대 아벨리안 피복 그래프입니다.^[10]

단위 거리 그래프로

3차원 정수 격자의 단위 거리 그래프에는 각 격자점에 대한 꼭지점이 있고, 각 꼭지점에는 정확히 6개의 이웃이 있습니다.격자에서 점들 중 일부를 제거할 수 있으므로, 각 나머지 점은 정확히 세 개의 인접한 부분을 가지며, 이 점들의 유도된 부분 그래프는 10개의 가장자리보다 짧은 주기를 갖지 않습니다.이렇게 하는 방법은 네 가지가 있는데, 그 중 하나는 라베스 그래프와 추상 그래프로 동형입니다.그러나 해당 정점은 더 대칭적이고 기존의 기하학적 구조와는 다른 위치에 있습니다.^[12]

라베스 그래프와 동형인 단순 입방정계의 또 다른 하위 그래프는 특정한 방법으로 가장자리의 절반을 제거함으로써 얻어집니다.반단순 입방 격자라고 불리는 결과 구조는 또한 라베스 그래프 자체보다 낮은 대칭성을 갖습니다.^[13]

특성.

라베스 그래프는 입방정계 그래프로 각 꼭지점에 정확히 3개의 모서리가 있음을 의미합니다.꼭짓점과 인접한 가장자리의 모든 쌍은 그래프의 대칭에 의해 다른 모든 쌍으로 변환될 수 있으므로 대칭 그래프입니다.보다 강력하게, $u{\displaystyle }$ ${\displaystyle u}$ 및 $v$ ${\displaystyle v}$의 두 정점에 대해 $u{\displaystyle }$ ${\displaystyle u}$에 결합된 세 모서리와$$ $v{\displaystyle }$ ${\displaystyle v}$에 결합된 세 모서리 사이의 모든 일대일 대응을 대칭으로 구현할 수 있습니다$$$.$그러나 전체적인 구조는 카이랄적입니다: 어떤 번역과 회전의 순서도 거울 이미지와 일치할 수 없습니다.^[10]라베스 그래프의 대칭 그룹은 공간 그룹 $I{\displaystyle }$ ${\displaystyle {\mathrm{}}_{}}$ 1 ${\displaystyle 32}$ ${\displaystyle I4_{1}32}$입니다$.$^[13]

이 구조의 둘레는 10입니다. 그래프에서 가장 짧은 사이클은 10개의 정점을 가지며, 이 중 15개의 사이클이 각 정점을 통과합니다.^[10][1][9](라베스 그래프의 좌표 순서를 구성하는) 임의의 정점에서 0, 1, 2, ...까지의 거리에 있는 정점의 수는 다음과 같습니다.^[14]

주변 공간을 각 꼭짓점에 가장 가까운 영역(이 구조의 보로노이 다이어그램의 셀)으로 분할하면, 이들은 각각 17개의 면을 가진 헵타데카데라를 형성합니다.그것들은 타일 공간이 나선형인 다면체인 플레시오헤드라입니다.이 다면체 물리학자 알란 쇤(Alan Schoen)이 형성한 구조를 실험하여 자이로이드 최소 표면을 발견했습니다.^[15] 자이로이드 최소 표면은 라베스 그래프의 가장자리를 실린더로 두껍게 하고 그들의 결합의 경계를 취함으로써 얻은 표면과 위상적으로 동등합니다.^[16]

Laves 그래프는 다음과 같은 의미에서 유일하게 짧은 삼중 주기 네트워크입니다.삼단주기는 공간의 모든 3차원에서 무한히 반복되는 것을 의미하므로 삼단주기 네트워크는 병진 대칭의 3차원 격자와 연결된 기하학적 그래프입니다.기본 도메인은 이러한 대칭 아래에서 변환된 복사본을 사용하여 공간을 타일링할 수 있는 형태입니다.모든 격자는 기본 도메인을 무한히 많이 선택할 수 있고 모양도 다양하지만 모두 $같은{\displaystyle }$ 볼륨$$V {\$displaystyle$ V$}$을(를) 갖습니다$.$ 기본 도메인의 복사본 하나 내에서 네트워크 가장자리의 길이를 측정할 수도 있습니다. 이 $숫자$를 L ${\displaystyle$ L}이라고 합니다$.$ V ${\displaystyle$ V$}$과 마찬가지로 $L{\displaystyle }$ ${\displaystyle L}$은$($는) 그렇지 않습니다.도메인 경계가 길이의 일부를 포함하지 않고 가장자리만 통과하는 한 기본 도메인의 선택에 따라 달라집니다.라베스 그래프에는 정점(orbit)의 4개의 대칭 클래스가 있는데, 여기서 고려되는 대칭 클래스는 변환일 뿐 이 4개의 클래스를 서로 매핑하는 데 필요한 회전이 아니기 때문입니다.각 대칭 클래스에는 기본 도메인에 하나의 꼭짓점이 있으므로 기본 도메인에는 총 길이 ${\displaystyle 62\sqrt{\mathrm{}}}$ ${\$의 12개의 반 모서리가 포함됩니다$.$기본 도메인의 볼륨은 32입니다.이 두 숫자에서 $L{\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$/ ${\displaystyle V}$ ${\displaystyle L^{3}/V}($무차원 수량)의 비율은 따라서 ${\displaystyle 27\sqrt{\mathrm{}}}$/ 2 ${\$ / ${\sqrt {2}}$입니다$.$ 이는 실제로 가능한 최소 값입니다.모든 3중 주기적 네트워크는

라브 그래프의 경우에만 동일하게 적용할 수 있습니다.^[17]

물리적 예시

예체능

야코부스 베르호프와 그의 아들 톰 베르호프가 만든 대나무 조각이라는 제목의 조각상은 다양한 색깔의 서로 연결된 아크릴 삼각형으로 그 꼭짓점을 나타내는 라베스 그래프의 조각 형태입니다.그것은 아인트호벤 공과대학에 2013년에 설치되었습니다.^[18]

분자 결정

라베스 그래프는 탄소의 동소체로 제시되고 있는데, 이는 120°각에서 원자당 3개의 결합을 갖는 일반적인 그래핀 및 흑연 탄소 구조와 유사합니다.^[3][5]그래핀에서 인접한 원자들은 서로 같은 결합면을 가지고 있는 반면, 라베스 그래프 구조에서는 인접한 원자들의 결합면이 결합선을 중심으로 대략 70.5°의 각도로 꼬여 있습니다.하지만 이 가상의 탄소 동소체는 불안정한 것으로 밝혀졌습니다.^[19]

라베스 그래프는 붕소에 대한 결정 구조를 제공할 수도 있는데, 계산 결과 안정적이어야 할 것으로 예상됩니다.^[20]이 구조를 형성할 수 있는 다른 화학 물질에는 SrSi₂("srnet" 이름이 유래) ^[8]및 질소 원소,^[9][20] 특정 금속-유기 골격체^[21] 및 순환 탄화수소가 포함됩니다.^[22]

Laves 그래프의 타이트-바인딩 모델에 대한 전자 밴드 구조가 연구되었으며, 이 구조에서 Dirac 및 Weyl 포인트의 존재를 보여줍니다.^[23][24]

다른.

라베스 그래프의 구조와 이로부터 파생된 자이로이드 표면도 비누-물 시스템과 나비 날개 비늘의 키틴 네트워크에서 실험적으로 관찰되었습니다.^[9]

참고문헌

외부 링크

• Hart, George W., The (10, 3)-a Network.
• Sloane, N. J. A. (ed.), "Sequence A046944 (Number of self-avoiding walks of length n on the Laves graph)", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation
• Sloane, N. J. A. (ed.), "Sequence A290705 (Theta series of triamond)", The On-Line Encyclopedia of Integer Sequences, OEIS Foundation