육각형 타일링

육각형 타일링

유형	일반 타일링
정점 구성	6.6.6 (또는³ 6)
얼굴 구성	V3.3.3.3(또는⁶ V3)
슐레플리 기호	{6,3} t{3,6}
와이토프 기호	3 6 2 2 6 3 3 3 3
콕서터 다이어그램
대칭	p6m, [6,3], (*632)
회전 대칭	p6, [6,3]⁺, (632)
듀얼	삼각 타일링
특성.	정점-추이적, 모서리-추이적, 면-추이적

기하학에서, 육각형 타일링 또는 육각형 테셀레이션은 정확히 세 개의 육각형이 각 정점에서 만나는 유클리드 평면의 규칙적인 타일링이다.슐레플리 기호는 ${6,3}$ $또는$ t ${3,6}($ 잘린 삼각형 타일링)입니다.

영국의 수학자 존 콘웨이는 그것을 헥틸이라고 불렀다.

육각형의 내부 각도는 120도이므로, 한 점에 세 개의 육각형이 360도를 이룬다.그것은 비행기의 세 개의 일반 타일링 중 하나입니다.나머지 두 개는 삼각형 타일링과 정사각형 타일링입니다.

적용들

육각형 타일링은 원을 2차원으로 배열하는 가장 밀도 높은 방법입니다.벌집형 추측은 육각형 타일링이 표면을 총 둘레가 최소인 동일한 영역의 영역으로 분할하는 가장 좋은 방법임을 나타냅니다.Kelvin 경은 Kelvin 구조(또는 체심 입방 격자)가 최적이라고 믿고 벌집(또는 비누 거품)을 만들기 위한 최적의 3차원 구조를 조사했습니다.하지만, 덜 규칙적인 Weaire-Phelan 구조가 약간 낫다.

이 구조는 그래핀의 각 판이 강한 공유 탄소 결합을 가진 닭 철사와 비슷한 흑연의 형태로 자연적으로 존재합니다.관 모양의 그래핀 시트가 합성되었습니다. 이것들은 탄소 나노튜브라고 알려져 있습니다.높은 인장 강도 및 전기적 특성으로 인해 많은 잠재적 용도가 있습니다.실리콘도 비슷해요.

치킨 와이어는 육각형 격자(일반적으로 일반이 아님)의 와이어로 구성됩니다.

가장 밀도가 높은 원 패킹은 이 타일링의 육각형처럼 배열됩니다.
닭줄 울타리
그래핀
카본나노튜브는 원통면상의 육각형 타일링으로 볼 수 있다.
육각형 페르시아 타일 c.1955

육각형 타일링은 많은 크리스탈에서 나타납니다.3차원에서는 면심 입방체 및 육각 밀착 패킹이 공통 결정 구조이다.그것들은 3차원에서 가장 밀도가 높은 구체 패킹입니다.구조적으로는 흑연 구조와 유사한 육각형 타일링의 병렬 층으로 구성됩니다.그들은 층이 서로 엇갈리는 방식으로 다르며, 면 중심의 입방체가 둘 중 더 규칙적이다.다른 물질들 중에서 순수한 구리는 면 중심의 입방체 격자를 형성합니다.

균일한 착색

육각형 타일링에는 세 가지 뚜렷한 균일한 색상이 있으며, 모두 위토프 구조의 반사 대칭에서 생성됩니다.(h,k)는 하나의 색깔 타일의 주기적인 반복을 나타내며, 육각형 거리를 h 첫 번째와 k 초로 셉니다.동일한 카운트는 Goldberg 다면체에서 _h,k{p+,3} 기법으로 사용되며 p > 6에 대한 쌍곡 타일링에 적용할 수 있습니다.

k자형	1소켓			2개소켓		3소켓
대칭	p6m, (*632)		p3m1, (*333)	p6m, (*632)		p6, (632)
사진.
색상	1	2	3	2	4	2	7
(h,k)	(1,0)	(1,1)		(2,0)		(2,1)
슐레플리	{6,3}	t{3,6}	t{3^[3]}
와이토프	3 6 2	2 6 3	3 3 3
콕서터
콘웨이	H	t		cH=t6daH		wH=t6dsH

3색 타일링은 3차 퍼무토헤드론으로 이루어진 테셀레이션입니다.

모따기 육각형 타일링

모서리를 새로운 육각형으로 대체하여 다른 육각형 타일로 변환하는 모따기 육각형 타일링.한계에서는 원면이 사라지고 새로운 육각형은 마름모꼴로 변질되어 마름모꼴 타일이 된다.

모따기 육각형 타일링은 한계에서 마름모꼴 타일링으로 퇴화됩니다.

육각형(H)	모따기 육각형(cH)			롬비(daH)

관련 타일링

육각형은 6개의 삼각형 세트로 분할할 수 있습니다.이 프로세스를 통해 두 개의 2-균일 타일링과 삼각형 타일링이 생성됩니다.

일반 타일링	절개요	이광자 타일링		일반 타일링	삽입	듀얼 타일링
원래의		3분의 1을 해부했다.	2/3 해부 완료	완전히 해부되었다		E에서 IH로, FH에서 H로

육각형 타일링은 마름모꼴 타일링의 각 정점이 새로운 모서리로 늘어나는 길쭉한 마름모꼴 타일링으로 간주할 수 있습니다.이것은 3차원에서의 마름모꼴 12면체와 마름모꼴 12면체 테셀레이션의 관계와 유사합니다.

마름모꼴 타일링	육각형 타일링	펜싱은 이 관계를 이용한다.

또한 특정 육각형 타일링의 원타일을 2개, 3개, 4개 또는 9개의 동일한 펜타곤으로 세분할 수 있습니다.

정육각형(각각 2개의 펜타곤으로 구성됨)의 오버레이가 있는 오각형 타일 유형 1.	정육각형(각각 3개의 펜타곤으로 구성됨)의 오버레이가 있는 오각형 타일링 타입 3.	반정형 육각형(각각 4개의 펜타곤으로 구성됨)의 오버레이가 있는 오각형 타일링 타입 4.	2가지 크기의 정육각형(각각 3과 9의 펜타곤 포함) 오버레이가 있는 오각형 타일 타입 3.

대칭 돌연변이

이 타일링은 육각형 타일링에서 시작하여 슐레플리 기호 {6,n} 및 콕서터 다이어그램이 무한대로 진행되는 육각형 면의 규칙 타일링 시퀀스의 일부로 위상적으로 관련되어 있습니다.

*n62 정규타일링 대칭변환: {6,n} v t
구면	유클리드	쌍곡선 타일링
{6,2}	{6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}	...	{6,∞}

이 타일링은 쌍곡면으로 이어지는 시퀀스의 일부로서 정점 도형이³ n인 정다면체와 위상적으로 관련되어 있습니다.

*n32 정규 타일링 대칭 변환: {n,3} v t
구면				유클리드	콤팩트 쌍곡선		파라코	비콤팩트 쌍곡선

{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

이는 정점 그림 n.6.6을 갖는 균일한 잘린 다면체와 유사하다.

*n32 잘린 타일링 대칭 돌연변이: n.6.6 v t
Sym. *n42 [n,3]	구면				유클리드	작은		파라크	비콤팩트 쌍곡선
Sym. *n42 [n,3]	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]	[12i, 3]	[9i, 3]	[6i, 3]
잘렸다 수치
설정.	2.6.6	3.6.6	4.6.6	5.6.6	6.6.6	7.6.6	8.6.6	∞.6.6	12i.6.6	9i.6.6	6i.6.6
n개 수치
설정.	V2.6.6	V3.6.6	V4.6.6	V5.6.6	V6.6.6	V7.6.6	V8.6.6	V†.6.6	V12i.6.6	V9i.6.6	V6i.6.6

이 타일링은 또한 잘린 마름모꼴 다면체와 [n,3] 콕서터 군 대칭을 가진 타일링 시퀀스의 일부이다.입방체는 마름모가 정사각형인 마름모꼴 육면체로 볼 수 있다.잘린 형태는 잘린 정점에 규칙적인 n-곤과 비정규적인 육각형 면을 가집니다.

이중 준규격 타일링 대칭 돌연변이: V(3.n)²
*n32	구면			유클리드	쌍곡선
*n32	*332	*432	*532	*632	*732	*832...	*∞32
타일링
컨피규정.	V(3.3)²	V(3.4)²	V(3.5)²	V(3.6)²	V(3.7)²	V(3.8)²	V(3.★)²

육각형 및 삼각 타일링으로 위토프 시공

균일한 다면체와 마찬가지로 정육각형 타일링(또는 이중 삼각형 타일링)을 기준으로 할 수 있는 8개의 균일한 타일링이 있습니다.

원래 면에 빨간색, 정점에 노란색, 모서리를 따라 파란색으로 색칠한 타일을 그리면 위상적으로 구별되는 8가지 형태가 있습니다(잘린 삼각형 타일은 위상적으로 육각형 타일과 동일합니다).

균일한 육각형/삼각형 타일링
근본적인 도메인	대칭: [6,3], (*632)							[6,3]⁺, (632)
	{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}


설정.	6개³	3.12.12	(6.3)²	6.6.6	3개⁶	3.4.6.4	4.6.12	3.3.3.3.6

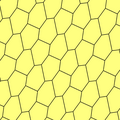
일면 볼록 육각형 타일링

일면 볼록 육각형 타일링에는 ^[1]3가지 유형이 있습니다.그것들은 모두 이등면체이다.각각은 고정된 대칭 안에서 파라메트릭 변형이 있습니다.유형 2는 활공 반사를 포함하며 키랄 쌍을 구별하는 2-이등면체입니다.

일면 볼록 육각형 타일링 3종
1	2		3
p2, 2222	pgg, 22×	p2, 2222	p3, 333

b = e B + C + D = 360°	b = e, d = f B + C + E = 360°		a = f, b = c, d = e B = D = F = 120°
이원 격자	4자 격자		3자 격자

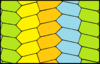
위상 등가 타일링

육각형 타일링은 정규 타일링과 동일한 {6,3} 토폴로지를 사용하여 만들 수 있습니다(각 정점 주위에 3개의 육각형 타일링).등면체 면에는 13가지 변형이 있습니다.주어진 대칭은 모든 면이 같은 색이라고 가정합니다.여기서 색상은 격자 ^[2]위치를 나타냅니다.단색(1타일) 격자는 평행 6각형입니다.

등각타일 육각형 13개
pg(××)	p3 (333)	pmg(22*)

pgg(22×)	p31m(3*3)	p2(2222)	cmm(2*22)	p6m(*632)

다른 등각 타일 위상 육각형 타일링은 에지 투 에지가 아닌 4변형 및 펜타곤으로 표시되지만 선형 인접 에지로 해석됩니다.

등각타일 사변형
pmg(22*)		pgg(22×)			cmm(2*22)	p2(2222)
평행사변형	사다리꼴	평행사변형	직사각형	평행사변형	직사각형	직사각형

등각 타일 펜타곤
p2(2222)	pgg(22×)	p3 (333)

2-균일 테셀레이션과 3-균일 테셀레이션은 회전 자유도를 가지며, 6각형의 ^[3]모서리 대 모서리 타일링으로 볼 수 있는 선형 케이스를 포함하여 6각형의 2/3를 왜곡합니다.

또한 키랄 4색 3방향 직조 패턴으로 왜곡되어 일부 육각형은 평행사변형으로 왜곡될 수 있습니다.2가지 색상의 면을 가진 직조 패턴은 회전 대칭이 632(p6)입니다.쉐브론 패턴은 pmg(22*) 대칭을 가지며, 3색 또는 4색 타일에 의해 p1(°)로 낮아진다.

규칙적인.	회전했다	규칙적인.	짜다	쉐브론
p6m, (*632)	p6, (632)	p6m(*632)	p6(632)	p1(°)

p3m1, (*333)	p3, (333)	p6m(*632)	p2(2222)	p1(°)

서클 패킹

육각형 타일링은 모든 점의 중심에 동일한 직경의 원을 배치하여 원 패킹으로 사용할 수 있습니다.모든 원은 패킹 내의 다른 3개의 원(키스 번호)^[4]과 접촉합니다.각 육각형 내부의 간격은 하나의 원을 허용하며, 삼각형 타일링에서 가장 밀도가 높은 패킹을 만듭니다. 각 원은 최대 6개의 원으로 접촉합니다.

「」를 참조해 주세요.

레퍼런스

^ 타일링 및 패턴, 9.3절 볼록 폴리곤에 의한 기타 일면체 타일링
^ 타일링 및 패턴, 107개의 등면체 타일링 목록에서 473–481페이지
^ 타일링 및 패턴, 모서리 대 모서리가 아닌 균일한 타일링
^ Order in Space: 디자인 소스 북, Keith Critchlow, 74~75페이지, 패턴 2
^ 콕서터, 정규 복합 폴리토피스, 페이지 111–112, 페이지 136.

Coxeter, H.S.M. Regular Polytopes, (3판, 1973년), Dover판, ISBN0-486-61480-8 페이지 296, 표 II: 일반 벌집
Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (제2.1장: 정규 및 균일한 타일링, 58–65페이지)
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 35. ISBN 0-486-23729-X.
John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1]

외부 링크

Weisstein, Eric W. "Hexagonal Grid". MathWorld.
- Weisstein, Eric W. "Regular tessellation". MathWorld.
- Weisstein, Eric W. "Uniform tessellation". MathWorld.
Klitzing, Richard. "2D Euclidean tilings o3o6x – hexat – O3".

v t 치수 2-9의 기본 볼록 규칙적이고 균일한 벌집
공간	가족	$({displaystyle {A}}_{n-1})$	$({displaystyle {C}}_{n-1})$	$(\displaystyle {B}}_{n-1})$	$({displaystyle {D}}_{n-1})$	$($ 스타일 ${G}_{2})$ / $($ 스타일 { $F}_{4})$ / $($ 스타일 ${E}_{n-1})$
E².	균일한 타일링	{3^[3]}	δ₃	할₃ 수 있다	문제₃	육각형
E³.	균일한 볼록한 벌집	{3^[4]}	δ₄	할₄ 수 있다	문제₄
E⁴.	균일한 4-허니콤	{3^[5]}	δ₅	할₅ 수 있다	문제₅	24셀 벌집
E⁵.	균일한 5벌집	{3^[6]}	δ₆	할₆ 수 있다	문제₆
E⁶.	균일한 6벌집	{3^[7]}	δ₇	할₇ 수 있다	문제₇	2개₂₂
E⁷.	균일한 7벌집	{3^[8]}	δ₈	할₈ 수 있다	문제₈	1₃₃ • 3₃₁
E⁸.	균일한 8벌집	{3^[9]}	δ₉	할₉ 수 있다	문제₉	1₅₂ • 2₅₁ • 5₂₁
E⁹.	균일한 9벌집	{3^[10]}	δ₁₀	할₁₀ 수 있다	문제₁₀
E¹⁰.	균일한 10벌집	{3^[11]}	δ₁₁	할₁₁ 수 있다	문제₁₁
E^n-1.	균일한 (n-1)-벌집	{3^[n]}	δ_n	할_n 수 있다	문제_n	1_k2 • 2_k1 • k₂₁

[1] 타일링 및 패턴, 9.3절 볼록 폴리곤에 의한 기타 일면체 타일링

[2] 타일링 및 패턴, 107개의 등면체 타일링 목록에서 473–481페이지

[3] 타일링 및 패턴, 모서리 대 모서리가 아닌 균일한 타일링

[Critchlow-4] Order in Space: 디자인 소스 북, Keith Critchlow, 74~75페이지, 패턴 2

[5] 콕서터, 정규 복합 폴리토피스, 페이지 111–112, 페이지 136.

[1]

[2]

[3]

[4]

[5]

Search

육각형 타일링

네임스페이스

더

목차

적용들

균일한 착색

모따기 육각형 타일링

관련 타일링

대칭 돌연변이

육각형 및 삼각 타일링으로 위토프 시공

일면 볼록 육각형 타일링

위상 등가 타일링

서클 패킹

관련 정규 복합 아페이로곤

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

육각형 타일링

적용들

균일한 착색

모따기 육각형 타일링

관련 타일링

대칭 돌연변이

육각형 및 삼각 타일링으로 위토프 시공

일면 볼록 육각형 타일링

위상 등가 타일링

서클 패킹

관련 정규 복합 아페이로곤

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.