선형함수(미적분)

y(x)=-x+2

함수의 그래프:

y(x)=-x+2

x

y(x)=-x+2

)

y(x)=-x+2

=

y(x)=-x+2

-

y(x)=-x+2

+

y(x)=-x+2

{\displaystyle y(x)=-x+2

}

수학의 미적분 및 관련 영역에서, 실제 숫자에서 실제 숫자에 이르는 선형 함수는 그래프(카르트 좌표에서)가 평면의 비수직선인 함수다.^[1]선형함수의 특성 특성은 입력 변수가 변경될 때 출력의 변화가 입력의 변화에 비례한다는 것이다.

선형 함수는 선형 방정식과 관련이 있다.

특성.

선형 함수는 변수 $x$ 가 최대 1:^[2]00을 갖는 다항식 함수다.

f(x)=ax+b

(

f(x)=ax+b

)

f(x)=ax+b

=

f(x)=ax+b

+ b

f(x)=ax+b

.

데카르트 평면에 있는 모든 $(x,f(x))$ 점 $(x,f(x))$ , f $(x,f(x))$ ( x $(x,f(x))$ ) $(x,f(x))$ 의 집합인 그래프가 선이기 때문에 이러한 함수를 선형이라고 한다.계수 a를 함수와 선의 기울기라고 한다(아래 참조).

기울기가 $a=0$ = $a=0$ $a=0$ 인 경우 $a=0$ $f(x)=b$ 은 수평선을 정의하는 $f(x)=b$ 상수 $f(x)=b$ f $f(x)=b$ $f(x)=b$ ) $f(x)=b$ = b $f(x)=b$ 이며, 일부 작성자는 선형 함수의 클래스에서 제외한다.^[3]이 정의에서, 선형 다항식의 정도는 정확히 1이 될 것이고, 그 그래프는 수직도 수평도 아닌 선일 것이다.그러나 이 글에서는 $a\neq 0$ $a\neq 0$ $a\neq 0$ 이(가) 필요하므로 $a\neq 0$ 상수 함수는 선형 함수로 간주된다.

$b=0$ = $b=0$ $b=0$ 일 $b=0$ 경우 선형 함수는 동종이라고 한다.그러한 함수는 좌표계의 원점, 즉 점( $(x,y)=(0,0)$ , $(x,y)=(0,0)$ y $(x,y)=(0,0)$ ) = ( $(x,y)=(0,0)$ 0 $(x,y)=(0,0)$ , $(x,y)=(0,0)$ ) $디스플레이스타일(x,y)=(0,0)}$ 을 통과하는 선을 정의한다 $(x,y)=(0,0)$ 고급 수학 문헌에서 선형함수라는 용어는 특별히 동질적인 선형함수를 나타내는 반면, 아핀함수라는 용어는 일반적인 경우에 사용하는데, 이를 포함한다.des $b\neq 0$ $b\neq 0$ $b\neq 0$ ${\displaystyle b\neq$ 0 $b\neq 0$

$x$ 에 허용된 입력 값 집합인 $f(x)$ 선형 함수 f( $f(x)$ ) ${\displaystyle$ f( $x)}$ 의 자연 $x\in \mathbb {R} .$ 은 x $x\in \mathbb {R} .$ $x\in \mathbb {R} .$ . $x\in \mathbb {R} .}.$ 임의 $x\in \mathbb {R} .$ 필드에서 $x$ 를 사용하여 계수 $a, b$ 를 갖는 기능도 고려할 수 있다.

그래프 $y=f(x)=ax+b$ = $y=f(x)=ax+b$ $y=f(x)=ax+b$ ) $y=f(x)=ax+b$ = $y=f(x)=ax+b$ + $y=f(x)=ax+b$ $y=f(x)=ax+b$ 은 y축의 y 절편점 $(x,y)=(0,b).$ $(x,y)=(0,b).$ ) $(x,y)=(0,b).$ = $(x,y)=(0,b).$ $(x,y)=(0,b).$ ) $(x,y)=(0,b).$ . ${\displaystyle(x,y)=(0,b$ )}과 정확히 하나의 교차점을 갖는 비수직선이다 $y=f(x)=ax+b$ $.$ $}$ y 절편 값 $y=f(0)=b$ = $y=f(0)=b$ ( 0 $y=f(0)=b$ ) $y=f(0)=b$ = b $y=f(0)=b$ 의 $(x,y)=(0,b).$ 초기 값도 $f(x).$ ( $f(x).$ ) $f(x).$ . ${\displaystyle f(x$ )라고 한다 $y=f(0)=b$ $.$ $}$ $a\neq 0,$ $a\neq 0,$ $a\neq 0,$ 인 $f(x).$ $a\neq 0,$ 경우 그래프는 x축, $(x,y)=(-{\tfrac {b}{a}},0).$ (x , $(x,y)=(-{\tfrac {b}{a}},0).$ y $(x,y)=(-{\tfrac {b}{a}},0).$ ) $(x,y)=(-{\tfrac {b}{a}},0).$ = $(x,y)=(-{\tfrac {b}{a}},0).$ ( $(x,y)=(-{\tfrac {b}{a}},0).$ - b $(x,y)=(-{\tfrac {b}{a}},0).$ , $(x,y)=(-{\tfrac {b}{a}},0).$ ) $(x,y)=(-{\tfrac {b}{a}},0).$ . ${\displaystyle(x,y)=(-{\tfrac {b}{na},0$ )과 정확히 하나의 교차점을 갖는 수평선이 아니다 $.$ $}$ x $(x,y)=(-{\tfrac {b}{a}},0).$ 절편 값 $x=-{\tfrac {b}{a}},$ = $x=-{\tfrac {b}{a}},$ - $x=-{\tfrac {b}{a}},$ a $x=-{\tfrac {b}{a}},$ , ${\displaystyle$ x $=-{\tfrac$ { $f(x)=0,$ $}{a},}$ 등식 f $f(x)=0,$ $f(x)=0,$ ) $f(x)=0,$ = 0 $f(x)=0,$ ${\displaystyf(x)=0,}$ 의 해법은 $x=-{\tfrac {b}{a}},$ $f(x).$ $f(x).$ )의 루트 또는 0이라고도 한다 $f(x).$ ${\displaystystyle$ f $(x).$ $}$

경사

선의 기울기는

x

의 변화,

\Delta x

\Delta x

{\

displaystyle {\tfrac {\deltay}{\Delta x

}

과

{\tfrac {\Delta y}{\Delta x}}

\Delta x

와)

상응

하는 y의

\Delta y

, Δ y {\

displaystyle

\

Delta

y} 사이의 비율 Δ

\Delta y

\Delta y

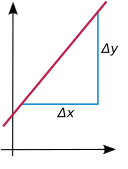
비수직 선의 기울기는 선이 얼마나 가파르게 기울어져 있는지(상승 오버런)를 측정하는 숫자다. $선$ 이 선형 함수 $f(x)=ax+b$ ( $f(x)=ax+b$ ) $f(x)=ax+b$ = $f(x)=ax+b$ + $f(x)=ax+b$ 의 $그래프$ 인 경우 $,$ 이 기울기는 상수 $a$ 에 $의해$ 주어진다 $f(x)=ax+b$

The slope measures the constant rate of change of $f(x)$ per unit change in x: whenever the input $x$ is increased by one unit, the output changes by $a$ units: $f(x{+}1)=f(x)+a$ , and more generally ${\displaystyle f(x{+}\Delta x)=f(x)$ 임의의 숫자 $\Delta x$ $\Delta x$ $\Delta x$ 에 $f(x{+}\Delta x)=f(x)+a\Delta x$ 대해 $+a\Delta x$ $\Delta x$ 기울기가 $a>0$ 이면 > $a>0$ 0 ${\displaystyle a>0$ 함수 f $f(x)$ ) ${\displaystyf$ $f$ $(x)}$ 이 $f(x)$ $a<0$ 하며, $a<0$ < $a<0$ ${\$ $displaystystyle$ $a<0$ $f(x)$ 이 감소하고 있다 $f(x)$ .

미적분학에서 일반함수의 파생상품은 그 변화율을 측정한다. $f(x)=ax+b$ 함수 $f(x)=ax+b$ x $f(x)=ax+b$ ) $f(x)=ax+b$ = $f(x)=ax+b$ + $f(x)=ax+b$ $f(x)=ax+b$ 은 기울기 $a$ 와 같은 일정한 변화율을 가지므로 $f(x)=ax+b$ , 그 파생상품은 상수 함수 $f\,'(x)=a$ ′ ( $f\,'(x)=a$ x $f\,'(x)=a$ ) $f\,'(x)=a$ = $f\',(x)=a$ 이다 $f\,'(x)=a$

미분학의 기본 개념은 매끄러운 함수 f( $f(x)$ ) ${\displaystyle f(x)}($ 필수 선형적이지 않음)는 고유한 선형 함수에 의해 $x=c$ 주어진 점 $x=c$ = c ${\displaystyle$ x $=c}$ 에 가깝게 근사하게 추정될 수 있다는 것이다.파생상품 $f\,'(c)$ $f\,'(c)$ ( $f\,'(c)$ $f\,'(c)$ ${\$ $displaystyle f$ $\},(c)}$ 은 이 선형함수의 기울기로 $f\,'(c)$ , $x\approx c$ 는 x $x\approx c$ $f(x)\approx f\,'(c)(x{-}c)+f(c)$ $x\approx c$ $f(x)\approx f\,'(c)(x{-}c)+f(c)$ ) $f(x)\approx f\,'(c)(x{-}c)+f(c)$ f $f(x)\approx f\,'(c)(x{-}c)+f(c)$ ( $c$ $f(x)\approx f\,'(c)(x{-}c)+f(c)$ (x - $f(x)\approx f\,'(c)(x{-}c)+f(c)$ c $f(x)\approx f\,'(c)(x{-}c)+f(c)$ + $f(x)\approx f\,'(c)(x{-}c)+f(c)$ ( $)\traft f\c)(x{-}c)+f(c)}$ 이다 $f(x)\approx f\,'(c)(x{-}c)+f(c)$ $x\approx c$ 선형 근사치의 그래프는 그래프 $y=f(x)$ = $y=f(x)$ ( $y=f(x)$ ) $y=f(x)$ 의 점 $(c,f(c))$ f $(c,f(c))$ ) ${\displaystyle (c,f(c)})$ 에 $y=f(x)$ 있는 접선 선입니다 $(c,f(c))$ 파생 경사 f $f\,'(c)$ (c $f\,'(c)$ ) $f\",(c)$ 은 일반적으로 $f\,'(c)$ 지점 c에 따라 다르다.선형 함수는 $f\,'(x)=a$ 이 일정한 유일한 실제 함수로 특징지어질 수 있다: 모든 x에 $f\,'(x)=a$ $f\,'(x)=a$ $f\,'(x)=a$ x ) = ${\displaystyle$ f $\,(x)=a},$ b $b=f(0)$ 0 )에 $b=f(0)$ $f(x)=ax+b$ = $f(x)=ax+b$ + $(\$ $displaystyle$ $f$ $(x$ $)=$ $ax+$ $b$ $b=f(0)$

경사 절편, 점 기울기 및 2점 형식

$f(x)$ 선형 $f(x)$ f $f(x)$ ( x $f(x)$ ) $f(x)$ 는 다양한 속성을 표시하는 몇 가지 표준 공식으로 작성할 수 있다 $f(x)$ .가장 간단한 것은 경사 절편 형식이다.

f(x)=ax+b

(

f(x)=ax+b

)

f(x)=ax+b

=

f(x)=ax+b

+

f(x)=ax+b

{\displaystyle f(x)=ax+b

여기에서 즉시 경사 a와 초기 값 $f(0)=b$ ( $f(0)=b$ ) $f(0)=b$ = $f(0)=b$ ${\displaystyle$ f ( $0)=b}$ 을 $($ 를) 볼 수 있으며, 이 값은 $y=f(x)$ y = $y=f(x)$ ( $y=f(x)$ x )의 $y-display$ 이다 $y=f(x)$

경사 a와 알려진 하나의 값 $f(x_{0})=y_{0}$ $f(x_{0})=y_{0}$ $f(x_{0})=y_{0}$ ) $f(x_{0})=y_{0}$ = $f(x_{0})=y_{0}$ $f(x_{0})=y_{0}$ ${\$ 을(를) 지정하면 다음과 같이 포인트 슬로프 형식을 쓴다 $f(x_{0})=y_{0}$

f(x)=a(x{-}x_{0})+y_{0}

(

f(x)=a(x{-}x_{0})+y_{0}

)

f(x)=a(x{-}x_{0})+y_{0}

=

f(x)=a(x{-}x_{0})+y_{0}

(

f(x)=a(x{-}x_{0})+y_{0}

- x

f(x)=a(x{-}x_{0})+y_{0}

)

f(x)=a(x{-}x_{0})+y_{0}

+

f(x)=a(x{-}x_{0})+y_{0}

f(x)=a(x{-}x_{0})+y_{0}

{\

그래픽 용어로, 이 $y=f(x)$ 은 y $y=f(x)$ = f $y=f(x)$ ( $y=f(x)$ ) $y=f(x)$ 을(를) 경사로 하여 $y=f(x)$ 점 $(x_{0},y_{0})$ $(x_{0},y_{0})$ y $(x_{0},y_{0})$ ) ${\displaystyle (x_{0},y_{0}}})$ 을 통과한다 $(x_{0},y_{0})$

The two-point form starts with two known values $f(x_{0})=y_{0}$ and $f(x_{1})=y_{1}$ . One computes the slope $a={\tfrac {y_{1}-y_{0}}{x_{1}-x_{0}}}$ and inserts this into the point-slope 형식:

{\

+y_{0

Its graph $y=f(x)$ is the unique line passing through the points $(x_{0},y_{0}\!),(x_{1},y_{1}\!)$ . The equation $y=f(x)$ may also be written to emphasize the constant slope:

{\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}

- y

{\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}

{\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}

-

{\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}

0

{\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}

= y

{\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}

- y

{\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}

-

{\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}

-

{\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{0}}{x_{1}-x_{0}}}

0

{\

스타일

{\

frac

{\y_{0}{0}}}={\frac {y_{1}-

y_{0}}}={\frac {y_{1}-

y_{0}}}{x_{1

}-

x_{0

선형 방정식을 사용한 관계

선형 함수는 일반적으로 선형 관계를 갖는 $x,y$ $변수$ x, y ,y {\ $displaystyle$ x, $y}$ 을(를) 포함하는 실제적 문제에서 발생한다. 즉, $Ax+By=C$ $Ax+By=C$ A $Ax+By=C$ + $Ax+By=C$ = $Ax+By=C$ {\ $displaysty Ax+$ By $=C}$ 을(를) 준수하는 것이다 $Ax+By=C$ 만약 B $B\neq 0$ 0 $B\neq 0$ {\ $displaystylean B\neq$ 0 $B\neq 0$ 이 y에 대해 이 방정식을 해결할 수 있다.

y=-{\tfrac {A}{B}x+{\tfrac {C}{B}=ax+b,

where we denote $a=-{\tfrac {A}{B}}$ and $b={\tfrac {C}{B}}$ . That is, one may consider y as a dependent variable (output) obtained from the independent variable (input) x via a linear function: $y=f(x)=ax+b$ .In the xy-coordinate plane, the possible values of $(x,y)$ form a line, the graph of the function $f(x)$ . If $B=0$ in the original equation, the resulting line $x={\tfrac {C}{A}}$ is vertical, and cannot be written as $y=f(x)$ $y=f(x)$ = $y=f(x)$ ( $y=f(x)$ ) ${\displaystyle$ y $=f(x$

그래프 $y=f(x)=ax+b$ = $y=f(x)=ax+b$ ( $y=f(x)=ax+b$ ) $y=f(x)=ax+b$ = x $y=f(x)=ax+b$ + $y=f(x)=ax+b$ ${\displaystyle$ y $=f(x)=ax+b}$ 의 특성은 변수 x와 y로 해석할 수 있다 $y=f(x)=ax+b$ . $y=f(0)=b$ 절편은 $x=0$ = $x=0$ ${\displaystyle$ y $=$ f(0 $y=f(0)=b$ ) $y=f(0)=b$ = $y=f(0)=b$ b {\displaystyle $y$ $=f(0)=b}$ 에서 $y=f(0)=b$ 초기 값 y $y=f(0)=b$ = $y=f(0)=b$ = $0$ 기울기는 입력 x에서 단위 변화당 출력 y의 변화율을 측정한다.그래프에서 한 단위를 오른쪽으로 이동하면(xx X 1 증가) y-값이 a: 즉, $f(x{+}1)=f(x)+a$ + $f(x{+}1)=f(x)+a$ ) $f(x{+}1)=f(x)+a$ = f $f(x{+}1)=f(x)+a$ $f(x{+}1)=f(x)+a$ + $f(x{+}1)=f(x)+a$ 위로 이동한다 $f(x{+}1)=f(x)+a$ 음의 기울기 a는 x의 각 증가에 대해 y가 감소함을 나타낸다.

예를 들어 $y=-2x+4$ 함수 y $y=-2x+4$ = $y=-2x+4$ - $y=-2x+4$ $y=-2x+4$ + $y=-2x+4$ ${\displaystyle$ $y$ $=-2x+4}$ 의 기울기 $a=-2$ = $a=-2$ - 2 ${\displaystyle$ a $=-2$ y-절편 점 $, b$ ) $(0,b)=(0,4)$ = ( $(0,b)=(0,4)$ b ) = $(0,b)=(0,4)$ 4 $(0,b)=(0,4)$ ) ${\displaystyle$ $(0$ $,4$ ) $(0,b)=(0,4)$ 및 x 절편차점 $(2,0)$ 2 $,0)$ 이 있다 $y=-2x+4$ $(2,0)$

예

살라미와 소시지가 킬로그램당 6유로, 3유로라고 가정하고, 우리는 12유로어치를 사고 싶다.우리는 각각 얼마씩 구매할 수 있을까?살라미 xkg과 소시지 ykg의 가격이 총 12유로라면, €6×x + €3×y = €12이다.y에 대한 해결은 위와 같이 점 $y=-2x+4$ $y=-2x+4$ = $y=-2x+4$ - 2 $y=-2x+4$ + 4 {\ $displaystyle y=-2x$ 4}을(를) 제공한다.즉, 우리가 먼저 살라미 x의 양을 선택한다면 소시지의 양은 $y=f(x)=-2x+4$ y $y=f(x)=-2x+4$ = $y=f(x)=-2x+4$ ( x $y=f(x)=-2x+4$ ) $y=f(x)=-2x+4$ = $y=f(x)=-2x+4$ - $y=f(x)=-2x+4$ $y=f(x)=-2x+4$ + 4 ${\displaystyle$ y $=f(x)=-2x+4}$ 로 계산될 수 있다 $y=f(x)=-2x+4$ 살라미가 소시지보다 두 배 비싸기 때문에 살라미 1킬로만 넣으면 소시지가 2킬로 감소한다: $f(x{+}1)=f(x)-2$ (x $f(x{+}1)=f(x)-2$ ) $f(x{+}1)=f(x)-2$ = $f(x{+}1)=f(x)-2$ ) = f(x ) $f(x{+}1)=f(x)-2$ - $f(x{+}1)=f(x)-2$ ${\displaystyle f(x{+}1)=f(x$ )- $2$ .y 절충점 $(x,y)=(0,4)$ , y $(x,y)=(0,4)$ ) $(x,y)=(0,4)$ = $(x,y)=(0,4)$ ( 0 $(x,y)=(0,4)$ , $(x,y)=(0,4)$ ) $(x,y)=(0,4)$ 은 소시지를 4kg만 사는 것에 해당하며 $(x,y)=(0,4)$ , x 절충점 $(x,y)=(2,0)$ , y $(x,y)=(2,0)$ ) $(x,y)=(2,0)$ = $(x,y)=(2,0)$ ( $(x,y)=(2,0)$ , $(x,y)=(2,0)$ ) $(x,y)=(2,0)$ 은 살라미 2kg만 사는 것에 해당한다 $(x,y)=(2,0)$ .

그래프에는 원래 변수에 의미가 없는 x 또는 y의 음수 값이 있는 점이 포함되어 있다는 점에 유의하십시오(도살자에게 고기를 파는 것을 상상하지 않는 한).따라서 우리는 함수 $f(x)$ ( $f(x)$ ) $f(x)$ 을(를) $0\leq x\leq 2$ $0\leq x\leq 2$ $0\leq x\leq 2$ $0\leq x\leq 2$ $0\leq x\leq 2$ ${\displaystyle 0\leq$ x $\leq 2}$ 도메인으로 $f(x)$ 제한해야 한다 $0\leq x\leq 2$

또한 독립변수로 y를 선택하고 $0\leq y\leq 4$ $x=g(y)=-{\tfrac {1}{2}}y+2$ 를 $x=g(y)=-{\tfrac {1}{2}}y+2$ 할 수 $0\leq y\leq 4$ $x=g(y)=-{\tfrac {1}{2}}y+2$ 0 $display$ y 4 {\ $displaystyle x=g$ $y)=-{\tfrac{1}{2}}y+$ 2}}: $y+}$ 도메인 0 $x=g(y)=-{\tfrac {1}{2}}y+2$ $0\leq y\leq 4$ y $0\leq y\leq 4$ 4 ${\displaystyle$ 4} .

다른 종류의 기능과의 관계

변수의 계수가 0 $(\neq 0$ )이 아닌 경우, 선형 함수는 도 1 다항식(선형 다항식이라고도 함)으로 표시되며, 그렇지 않으면 상수 함수 - 또한 다항식 함수지만 0도인 것이다.

다른 종류의 좌표계로 그릴 때 직선은 다른 기능을 나타낼 수 있다.

예를 들어, 해당 값이 로그 척도로 표현될 때 지수 함수를 나타낼 수 있다. $로그 (g (x))$ 가 $x$ 의 선형 함수일 때 함수 $g$ 는 지수 함수를 의미한다.선형 함수의 경우 입력을 한 단위로 증가시키면 출력이 일정량 증가하는데, 이것은 함수의 그래프 경사다.지수함수의 경우 입력을 한 단위로 증가시키면 출력이 고정 배수로 증가하는데, 이를 지수함수의 베이스라고 한다.

함수의 인수와 값이 모두 로그 척도(예: $log (y)$ 가 로그 $(x$ )의 선형 함수인 경우)에 있는 경우, 직선은 다음과 같은 전력 법칙을 나타낸다.

\log_{r}y=a\log_{r}x+b\quad \Rightarrow \quad y=r^{b}\cdot x^{a}}}

극 방정식 r =에 의해 정의된 아르키메데스 나선1⁄2θ + 2

반면에 극좌표 측면에서 선형함수의 그래프는 다음과 같다.

#\displaystyle r=f(\theta )=a\theta +b}

$a\neq 0$ $a\neq 0$ ${\displaystyle a\neq$ 0 $}$ 일 경우 아르키메데스 나선형이고, 그렇지 $a\neq 0$ 않으면 원이 된다.

참고 항목

아핀 지도, 일반화
정수 인수의 선형 함수인 산술 수열

메모들

^ 스튜어트 2012, 23페이지
^ 스튜어트 2012, 페이지 24
^ Sokowski 1983, 페이지

참조

제임스 스튜어트(2012), 미적분학: 얼리 트랜스덴탈스, 7E판, 브룩스/콜레. ISBN 978-0-538-49790-9
Swokowski, Earl W. (1983), Calculus with analytic geometry (Alternate ed.), Boston: Prindle, Weber & Schmidt, ISBN 0871503417

외부 링크

[1] 스튜어트 2012, 23페이지

[2] 스튜어트 2012, 페이지 24

[3] Sokowski 1983, 페이지

[1]

[2]

[3]

v t 다항식 및 다항식 함수
정도별	0 다항식(도 정의되지 않음 또는 -1 또는 -multi) 상수 함수(0) 선형 함수(1) 선형 방정식 2차 함수(2) 이차 방정식 입방 함수(3) 입방정식 사분위 함수(4) 사분방정식 5중함수(5) Sextic 방정식(6) 정화 방정식 (7)
속성별	일변량 비바리아테 다변량 모노미알 이항체 삼원체 무레듀케이블 스퀘어 프리 동질적 준균종
도구 및 알고리즘	인자화 최대공통점 나누기 호너의 평가법 결과물 판별 그뢰브너 기준

Search