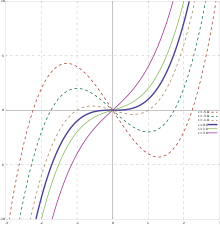
입방 함수

이 기사는 대체로 또는 전적으로 단일 출처에 의존한다. 관련 토론은 토크 페이지에서 찾을 수 있다. 추가 출처에 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오. 출처 찾기: "큐빅 함수" – 뉴스 · 신문 · 도서 · 학자 · JSTOR (1919년 9월)

수학에서 입방 함수는 형태의 함수다.

${\displaystyle f(x)=ax^{3}+bx^{2}+cx+d}$

여기서 계수 a, b, c, d는 복잡한 숫자로, 변수 x는 실제 값과 0 0을 취한다. 즉, 학위 3의 다항식 함수인 동시에 실제 함수인 것이다. 특히 도메인과 코도메인은 실수의 집합이다.

f(x) = 0을 설정하면 폼의 입방정식이 생성됨

${\displaystyle ax^{3}+bx^{2}+cx+d=0,}$

그 해답은 함수의 뿌리라고 불린다.

입방 함수는 하나 또는 세 개의 실제 뿌리를 가지고 있다(구분하지 않을 수 있음).^[1] 모든 홀수 도 다항식은 적어도 하나의 실제 뿌리를 가지고 있다.

입방 함수의 그래프에는 항상 단일 변곡점이 있다. 두 개의 임계 지점, 즉 국소 최소 지점과 국소 최대 지점을 가질 수 있다. 그렇지 않으면 입방 함수는 단조롭다. 입방 함수의 그래프는 변곡점에 대해 대칭이다. 즉, 이 점을 반 바퀴 돌면 불변한다. 아핀 변환까지 입방 함수에 대해 가능한 그래프는 세 개뿐이다.

입방 함수는 입방 보간술의 기본이다.

역사

임계점 및 변곡점

입방함수의 임계점은 고정점이며, 이는 함수의 기울기가 0인 지점이다.^[2] 따라서 다음과 같이 정의되는 입방 함수의 임계 점 f

f(x) = 도끼³ + bx² + cx + d,

x의 가치로 발생하여 파생상품이 된다.

${\displaystyle 3ax^{2}+2bx+c=0}$

입방 함수는 0이다.

이 방정식의 해법은 임계점의 x 값이며 2차 공식을 사용하여 다음과 같이 주어진다.

${\displaystyle x_{\text{critical}={\frac {-b\pm {\sqrt{b^{2}-3ac}}}{3a}}}.}$

제곱근 안에 있는 식의 기호가 임계점 수를 결정한다. 양성이면 두 개의 임계점이 있는데 하나는 국소 최대값이고 다른 하나는 국소 최소값이다. b² – 3ac = 0이면 임계점은 하나만 있으며, 이는 변곡점이다. b² – 3ac < 0이면, (실제) 임계점이 없다. 후자의 경우, 즉 b² – 3ac이 양성이 아닌 경우 입방 함수는 엄격히 단조롭다. 사례 Δ₀ > 0의 예는 그림을 참조한다.

함수의 변곡점은 함수가 동일성을 변화시키는 곳이다.^[3] 변곡점은 두 번째 파생상품 $f{\displaystyle {}^{}}$ ${\displaystyle ″(x}$)${\displaystyle }$= ${\displaystyle 6}$ ${\displaystyle a}$ x${\displaystyle }$+ ${\displaystyle 2}$ b${\displaystyle ,}$ ${\displaystyle f"(x)=6ax+2b,}$이(가) 0이고$$, 세 번째 파생상품이 0이 아닐 때 발생한다. 따라서 입방 함수는 항상 단일 변곡점을 가지며, 이 변곡점은 다음과 같다.

${\displaystyle x_{\text{inflection}=-{\frac {b}{3a}}.}$

분류

입방 함수의 그래프는 입방 곡선이지만 많은 입방 곡선은 함수의 그래프가 아니다.

입방 함수는 네 개의 모수에 따라 달라지지만, 그래프의 모양은 극소수일 뿐이다. 사실 입방 함수의 그래프는 항상 형태 함수의 그래프와 비슷하다.

${\displaystyle y=x^{3}+properties.}$

이러한 유사성은 좌표축에 평행한 번역, 균일성(균일성 스케일링), 그리고 Y축에 대한 반사(거울 이미지)의 구성으로 구축될 수 있다. 더 많은 균일하지 않은 스케일링은 그래프를 세 개의 입방 함수 중 하나의 그래프로 변환할 수 있다.

${\displaystyle {\regated}y&=x^{3}+x\\y&=x^{3}}\\y&=x^{3}-x.\end{정렬}}}$

이것은 아핀 변환까지 입방 함수의 그래프가 3개밖에 없다는 것을 의미한다.

위의 기하학적 변환은 ${\displaystyle \mathrm{일반}}$ 입방 함수 y${\displaystyle }$= ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$+ ${\displaystyle b}$ x ${\displaystyle {2\mathrm{}}^{}}$+ ${\displaystyle c}$+ ${\displaystyle d}$. ${\displaystyle$ y$=ax^{3}+bx^{2}+cx+d$로 시작할 때 다음과 같은 방법으로 빌드할 수 있다$.$$}$

첫째, < 0이면 변수 x → –x의 변경으로 a >를 가정할 수 있다. 이 변수 변경 후 새로운 그래프는 y축에 관해서 이전 그래프의 거울상이다.

그리고 나서, 변수 x의 변화)x1–.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .d.En{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}b/3a 형태의 기능을 제공한다.

${\displaystyle y=ax_{1}^{3}+{1}+q.}$

이것은 x축과 평행한 번역에 해당한다.

변수 y = y₁ + q의 변경은 y 축에 관한 번역에 해당하며, 폼의 함수를 제공한다.

${\displaystyle y_{1}=ax_{1}^{3}+{1}.}$

The change of variable ${\displaystyle \textstyle x_{1}={\frac {x_{2}}{\sqrt {a}}},y_{1}={\frac {y_{2}}{\sqrt {a}}}}$ corresponds to a uniform scaling, and give, after multiplication by ${\displaystyle {\sqrt {a}},}$ a function of the form

${\displaystyle y_{2}=x_{2}^{3}+{2}}$

유사성에 의해 얻을 수 있는 가장 단순한 형태다.

Then, if p ≠ 0, the non-uniform scaling ${\displaystyle \textstyle x_{2}=x_{3}{\sqrt { p }},\quad y_{2}=y_{3}{\sqrt { p ^{3}}}}$ gives, after division by ${\displaystyle \textstyle {\sqrt { p ^{3}}},}$

${\displaystyle y_{3}=x_{3}^{3}+x_{3}}}\snname {sgn}(p),}$

여기서 ${\displaystyle \mathrm{sgn}}$ ${\displaystyle }$( ${\displaystyle p}$) ${\displaystyle \operatorname {sgn}(p)}$은(는) p의 부호에 따라 값 1 또는 –1을$$ 갖는다. ${\displaystyle \mathrm{sgn}}$ ${\displaystyle (0}$) = ${\displaystyle \operatorname$ {$sgn}(0)=0}을($를) 정의하는 경우, 함수의 후자$$ 형식이 모든 경우에 적용된다($x2{\displaystyle {}_{}}$= ${\displaystyle {x\mathrm{}}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$ ${\$$x_$${3},$ ${\displaystyle y_{}}$ 2${\displaystyle {}_{}}$= ${\displaystyle {y\mathrm{}}_{}}$ 3 ${\displaysty_{3}).$

대칭

$y{\displaystyle }$= ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$+ p ${\displaystyle x}$, ${\displaystyle y=x^{3}+px$ 형식의 입방 함수의 경우$,$ 변곡점은$$ 따라서 원점이 된다. 그러한 함수는 홀수 함수이므로, 그 그래프는 변곡점에 대해 대칭이며 변곡점을 반 바퀴 도는 동안 불변함수다. 이러한 성질은 유사성에 의해 불변하므로, 모든 입방 함수에 대해 다음과 같은 것이 적용된다.

입방 함수의 그래프는 변곡점에 대해 대칭이며, 변곡점을 반 바퀴 돌 때 불변한다.

공선성

세 개의 시준점에서 입방 함수의 그래프에 대한 접선은 다시 시준점에서 입방체를 가로채게 된다.^[4] 이것은 다음과 같이 볼 수 있다.

이 특성은 경직된 운동 하에서 불변하므로, 함수 형태가 있다고 가정할 수 있다.

${\displaystyle f(x)=x^{3}+properties.}$

α가 실제 숫자일 경우, 점(α, f(α))에서 f의 그래프에 탄젠트가 선이다.

{(x, f(α) + (x - α)f ′(α) : x ∈ R}.

따라서 이 선과 f의 그래프 사이의 교차점은 f(x) = f(α) + (x - α)f α(α) 등식을 풀어서 얻을 수 있다.

${\displaystyle x^{3}+beat=\beat ^{3}+p\beat +(x-\beat)(3\beat ^{2}+p),}$

다시 쓸 수 있는

${\displaystyle x^{3}-3\reason ^{2}x+2\reason ^{3}=0,}$

로서 요소화된.

${\displaystyle (x-\property )^{2}(x+2\properties )=0.}$

그래서 접선은 입방체를 가로채고

$(-\displaystyle(-2\filename ,-8\filename ^{3}-2p\p\fline )=(-2\filename ,-8f(\filename )+6p\fdism.}$

그래프의 한 점(x, y)을 접선이 그래프를 가로채는 다른 점에 매핑하는 함수

$[\displaystyle (x,y)\mapsto (-2x,-8y+6인치)]}$

이것은 시준점을 시준점으로 변형시키는 아핀 변환이다. 이것은 청구된 결과를 증명한다.

입방 보간법

함수의 값과 함수의 파생값을 두 점으로 환산하면 정확히 하나의 입방 함수가 있으며, 4개의 값이 동일한 것을 입방형 헤르미테 스플라인이라고 한다.

이 사실을 이용하는 데는 두 가지 표준 방법이 있다. 첫째로, 물리적 측정, 예를 들어 어떤 샘플링 지점에서 함수의 값과 그 파생상품을 알고 있다면, 연속적으로 서로 다른 함수로 함수를 보간할 수 있는데, 그것은 조각과 같은 입방 함수다.

함수의 값이 여러 지점에서 알려진 경우, 입방 보간법은 연속적으로 다른 함수에 의해 함수에 근사치하는 것으로 구성된다. 고유하게 정의된 보간법을 가지려면 엔드포인트의 파생상품 값이나 엔드포인트의 곡률 0과 같은 두 가지 제약조건을 추가해야 한다.

참조

외부 링크

위키미디어 커먼즈에는 큐빅 기능과 관련된 미디어가 있다.

• "Cardano formula", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• MacTutor 아카이브의 2차 방정식, 입방정식 및 4차 방정식 역사.