링크/컷 트리

이 기사에는 참조, 관련 판독 또는 외부 링크 목록이 포함되어 있지만 인라인 인용이 없기 때문에 출처가 불분명합니다. 좀 더 정확한 인용문을 소개하여 이 기사를 개선하는 데 도움을 주시기 바랍니다. (2015년 10월) (이 템플릿 메시지를 제거하는 방법과 시기에 대해 알아보십시오.)

링크/컷 트리는 포리스트, 루트 트리 집합을 나타내기 위한 데이터 구조이며 다음 작업을 제공합니다.

• 단일 노드로 구성된 트리를 포리스트에 추가합니다.
• 트리 중 하나에 노드가 있으면 해당 노드(및 하위 트리)를 해당 노드가 속한 트리에서 분리합니다.
• 노드를 하위 노드로 다른 노드에 연결합니다.
• 노드가 주어지면 노드가 속한 트리의 루트를 찾습니다. 두 개의 서로 다른 노드에서 이 작업을 수행하면 동일한 트리에 속하는지 여부를 확인할 수 있습니다.

표현된 포리스트는 매우 깊은 트리로 구성될 수 있으므로 포리스트를 부모 포인터 트리의 일반적인 모음으로 표현하면 주어진 노드의 루트를 찾는 데 오랜 시간이 걸릴 수 있습니다. 그러나 숲의 각 트리를 링크/컷 트리로 표현하면 O(log(n)) 분할 시간에서 요소가 어느 트리에 속하는지 찾을 수 있습니다. 또한 링크/컷 트리의 수집을 표현된 숲의 변화에 맞춰 빠르게 조정할 수 있습니다. 특히 O(log(n)) 상각시간에 병합(링크) 및 분할(컷)하도록 조정할 수 있습니다.

링크/컷 트리는 표현된 포리스트의 각 트리를 정점-이종 경로로 분할하며, 각 경로는 보조 데이터 구조로 표현됩니다(종종 원래 논문은 분할 트리를 미리 지정하여 편향된 이진 검색 트리를 사용하지만). 보조 데이터 구조의 노드들은 해당 표현된 트리의 깊이에 따라 순서가 정해집니다. Nive Partitioning(나이브 파티셔닝)이라는 변형에서 경로는 Tango Tree와 유사하게 가장 최근에 액세스한 경로와 노드에 의해 결정됩니다. 크기별 파티셔닝에서 경로는 지정된 노드의 가장 무거운 자식(가장 많은 자식이 있는 자식)에 의해 결정됩니다. 이렇게 하면 구조가 더 복잡해지지만, 운영 비용이 상각된 O(logn)에서 최악의 경우 O(logn)로 줄어듭니다. 다양한 네트워크 흐름 문제를 해결하고 데이터 세트를 제공하는 데 사용됩니다.

원래 출판물에서 Sleator와 Tarjan은 링크/컷 트리를 "동적 트리" 또는 "동적 다이노 트리"라고 언급했습니다.

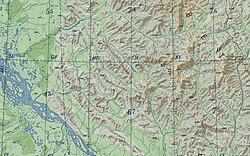
구조.

각 노드가 임의의 정도의 정렬되지 않은 노드를 갖는 트리를 선택하여 경로로 분할합니다. 우리는 이것을 표현된 나무라고 부릅니다. 이러한 경로는 내부적으로 보조 트리로 표시됩니다(여기서는 스플레이 트리를 사용합니다). 여기서 왼쪽에서 오른쪽으로 가는 노드는 루트에서 경로의 마지막 노드까지의 경로를 나타냅니다. 표시된 트리에서 연결된 노드 중 동일한 선호 경로에 있지 않은 노드(따라서 동일한 보조 트리에 있지 않음)는 경로-부모 포인터를 통해 연결됩니다. 이 포인터는 경로를 나타내는 보조 트리의 루트에 저장됩니다.

선호 경로

표현된 트리에서 노드 v에 대한 액세스가 이루어지면 선택한 경로가 기본 경로가 됩니다. 노드의 기본 자식은 액세스 경로에 있는 마지막 자식이거나 마지막 액세스가 v인 경우 또는 트리의 이 특정 가지에 대한 액세스가 이루어지지 않은 경우 null입니다. 선호하는 에지는 선호하는 자식을 v에 연결하는 에지입니다.

대체 버전에서 선호 경로는 가장 무거운 자식에 의해 결정됩니다.

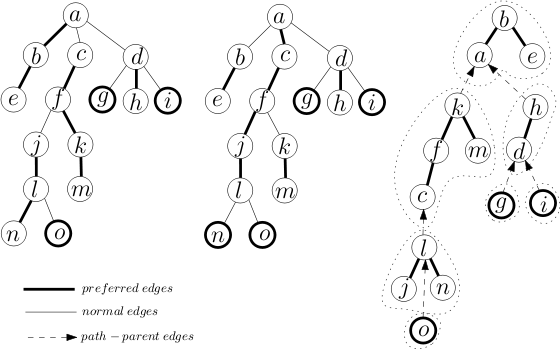
오퍼레이션스

관심 있는 작업은 FindRoot(Node v), Cut(Node v), Link(Node v, Node w) 및 Path(Node v)입니다. 모든 작업은 액세스(Node v) 서브루틴을 사용하여 구현됩니다. 정점 v에 액세스하면 표현된 트리의 기본 경로가 표현된 트리의 루트 R에서 노드 v로 이동하는 경로로 변경됩니다. 액세스 경로의 노드에 기본 하위 u가 이전에 있고 경로가 이제 하위 w로 이동하는 경우 기존의 기본 에지가 삭제됩니다(경로-부모 포인터로 변경됨). 그리고 새로운 길은 이제 w를 통과합니다.

접근

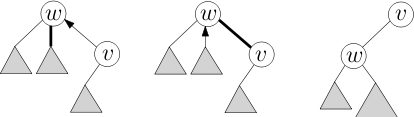
노드 v에 대한 액세스를 수행한 후에는 선호하는 자식이 더 이상 없으며 경로의 끝에 있게 됩니다. 보조 트리의 노드는 깊이별로 키가 지정되므로 보조 트리의 v 오른쪽에 있는 노드는 모두 연결이 끊어져야 합니다. 스플레이 트리에서 이것은 비교적 간단한 절차입니다. 우리는 v에서 스플레이를 하는데, 이것은 v를 보조 트리의 뿌리로 가져옵니다. 그런 다음 v의 오른쪽 부분 트리의 연결을 끊습니다. v는 이전 선호 경로에서 그 아래로 들어온 모든 노드입니다. 연결이 끊어진 트리의 루트에는 v를 가리키는 경로-부모 포인터가 있습니다.

이제 표현된 트리를 루트 R로 걸어 올라가며 필요한 경우 선호 경로를 중단하고 재설정합니다. 이를 위해 v의 경로-부모 포인터를 따릅니다(v는 이제 루트이므로 경로-부모 포인터에 직접 액세스할 수 있습니다). v가 있는 경로에 루트 R이 이미 포함되어 있는 경우(노드가 깊이별로 키가 지정되어 있으므로 보조 트리에서 가장 왼쪽에 있는 노드) 경로-부모 포인터가 null이고 액세스가 완료됩니다. 그렇지 않으면 포인터를 따라 다른 경로 w의 어떤 노드로 이동합니다. w의 오래된 선호 경로를 끊고 경로 von에 다시 연결하려고 합니다. 이를 위해 w에서 플레이하고 오른쪽 하위 트리를 분리하여 경로-부모 포인터를 w로 설정합니다. 모든 노드는 깊이별로 키가 설정되어 있고 v의 경로에 있는 모든 노드는 w의 경로에 있는 모든 노드보다 깊기 때문에(표시된 트리에서 w의 자식이므로) v의 트리를 w의 오른쪽 자식으로 연결하기만 합니다. 우리는 v를 다시 사용하는데, v는 뿌리 w의 자식이므로 단순히 v를 뿌리로 회전시킵니다. v의 경로-부모 포인터가 null이 될 때까지 이 전체 프로세스를 반복합니다. 이때 v는 표현된 트리 R의 루트와 동일한 선호 경로에 있습니다.

루트 찾기

FindRoot는 노드 v를 포함하는 표현된 트리의 루트를 찾는 것을 말합니다. 액세스 서브루틴은 v를 선호 경로에 놓으므로 먼저 액세스를 실행합니다. 이제 노드 v는 동일한 선호 경로 상에 있으며 따라서 루트 R과 동일한 보조 트리 상에 있습니다. 보조 트리는 깊이별로 키가 지정되므로 루트 R은 보조 트리의 가장 왼쪽 노드가 됩니다. 그래서 우리는 더 이상 진행할 수 없을 때까지 단순하게 왼쪽 자식을 선택하고, 이 노드가 루트 R입니다. 루트가 선형적으로 깊을 수 있으므로(스플레이 트리의 경우 최악의 경우) 다음 액세스가 신속하도록 루트를 스플레이합니다.

인하.

여기서 우리는 노드 v에서 표현된 트리를 자를 것입니다. 먼저 우리는 v에 접근합니다. 이렇게 하면 표시된 트리에서 v보다 낮은 모든 요소가 보조 트리에서 v의 오른쪽 자식으로 배치됩니다. v의 왼쪽 하위 트리에 있는 모든 요소는 표시된 트리의 v보다 높은 노드입니다. 따라서 v의 왼쪽 자식(경로-부모 포인터를 통해 여전히 원래 표시된 트리에 대한 첨부 파일을 유지함)의 연결을 끊습니다. 이제 v는 표현된 트리의 루트입니다. v에 액세스하면 v 아래의 기본 경로도 끊어지지만 해당 하위 트리는 해당 경로 상위 포인터를 통해 v에 대한 연결을 유지합니다.

링크

v가 트리의 뿌리이고 w가 다른 트리의 정점일 때, 간선 (v, w)를 추가하여 v와 w를 포함하는 트리들을 연결하고, w를 v의 부모로 만듭니다. 이를 위해서 우리는 각각의 트리에서 v와 w를 모두 액세스하고, w를 v의 왼쪽 자식으로 만듭니다. v는 루트이고, 노드는 보조 트리에서 깊이별로 키가 지정되므로, v에 액세스하면 v에 보조 트리에 남아 있는 자식이 없음을 의미합니다(루트가 최소 깊이이므로). 왼쪽 자식을 추가하면 표시된 트리에서 v의 부모가 됩니다.

경로.

이 작업을 위해 루트 R에서 노드 v로의 경로(예: "sum" 또는 "min" 또는 "max" 또는 "증가" 등)에 있는 모든 노드(또는 에지)에 대해 집계 기능을 수행하려고 합니다. 이를 위해서 우리는 v에 접근하는데, v는 루트 R에서 노드 v로의 경로에 있는 모든 노드를 가진 보조 트리를 제공합니다. 데이터 구조는 최소값 또는 최대값 또는 하위 트리의 비용 합계와 같이 검색하려는 데이터로 증강될 수 있으며, 이 데이터는 일정한 시간 내에 주어진 경로에서 반환될 수 있습니다.

연산의 의사코드

스위치-기본 설정-자녀(x, y):     (right(x)가 null이 아닌 경우)         path-parent(오른쪽(x)) = x     right(x) = y     (y가 null이 아닌 경우)         부모(y) = x 

액세스(v):     플레이(v)     스위치-선호-자녀(v, null)     (path-parent(v)가 null이 아닌 경우)          w = path-parent(v)         튀기다(w)         스위치-선호-자녀(w, v)         액세스(v) 

링크(v, w):     액세스(v)     접속(w)     left(v) = w     부모(w) = v 

절단(v):     액세스(v)     (left(v)가 null이 아닌 경우)         path-parent(왼쪽(v)) = path-parent(v)         left(v) = null     path-parent(v) = null 

분석.

절단 및 링크에는 O(1) 비용과 액세스 비용이 있습니다. FindRoot는 O(logn) 상각된 상한값과 액세스 비용이 있습니다. 데이터 구조는 구현에 따라 하위 트리의 최소값 노드 또는 합계와 같은 추가 정보로 증강될 수 있습니다. 따라서 Path는 이 정보를 액세스 바운드에 더하여 일정한 시간 내에 반환할 수 있습니다.

따라서 실행 시간을 찾기 위해 액세스를 제한해야 합니다.

액세스는 O(log n) 분할 상한이 있는 것으로 알려진 스플레이팅을 사용합니다. 그래서 남은 분석은 우리가 플레이해야 하는 횟수를 다룹니다. 이 값은 트리를 이동할 때 기본 자식 변경 수(기본 경로에서 변경된 에지 수)와 같습니다.

우리는 중광분해라는 기술을 사용하여 접근을 제한했습니다.

중광분해

이 기법은 서브트리의 노드 수에 따라 에지를 무겁거나 가볍게 부릅니다. ${\displaystyle \mathrm{크기}(v)}$ ${\displaystyleSize(v)}$은(는) 표시된 트리의 v 하위 트리에 있는 노드 수를 나타냅니다$$. 가장자리는 크기(v) >이면 무겁다고 합니다. 1 ⁄ 2 사이즈(부모(v)). 따라서 각 노드는 최대 1개의 무거운 에지를 가질 수 있음을 알 수 있습니다. 무거운 에지가 아닌 에지를 가벼운 에지라고 합니다.

광깊이는 뿌리에서 정점 v로 가는 주어진 경로의 광엣지 수를 나타냅니다. 광깊이 ≤ lgn은 광엣지를 통과할 때마다 노드 수가 최소 2배 감소하기 때문입니다(부모 노드의 절반 이상을 가질 수 있으므로).

따라서 표현된 트리의 주어진 가장자리는 무겁게 선호되는, 무겁게 선호되지 않는, 가볍게 선호되는, 또는 가볍게 선호되지 않는 네 가지 가능성 중 하나가 될 수 있습니다.

먼저 $O{\displaystyle (\log }$ ${\displaystyle 2^{}}$ ⁡ n) ${\displaystyle O(\log$^{2}n)} 상한을 증명합니다.

O(logn) 상한

액세스의 splay 연산은 log n을 주기 때문에, 우리는 O(log n) 상한을 증명하기 위해 log n에 대한 액세스 수를 제한해야 합니다.

선호 에지가 변경될 때마다 새로운 선호 에지가 형성됩니다. 그래서 우리는 형성된 선호 모서리의 수를 세고 있습니다. 주어진 경로에 밝은 최대 log n 에지가 있으므로 최대 log n 라이트 에지가 기본 설정으로 변경됩니다.

선호되는 헤비 에지의 수는 임의의 주어진 $작업$에 대해 ${\displaystyle O(}$n$)$ {\$display$ O($n)}$일 수 있지만${\displaystyle O}$(${\displaystyle \log }$ ⁡ n) {\$displaystyle$$O$(\log n)}은(는) 상각됩니다. 일련의 실행에서 n-1개의 무거운 에지가 선호될 수 있지만(표시된 트리에 총 n-1개의 무거운 에지가 있기 때문에), 그 이후로 선호되는 무거운 에지의 수는 이전 단계에서 선호되지 않게 된 무거운 에지의 수와 동일합니다. 선호되지 않는 모든 무거운 모서리에 대해 가벼운 모서리가 선호되어야 합니다. 선호될 수 있는 밝은 모서리의 수는 최대 logn임을 이미 확인했습니다. 따라서 m 작업에서 선호되는 무거운 에지의 $수$는 m${\displaystyle (\log }$ ⁡ ${\displaystyle n)}$ +${\displaystyle }$(n$$- 1) ${\displaystyle$ m(\log$$n$)+($n-1)}입니다. 작업이 충분하면(m > n - 1 {\display m> n-1}) 이 평균은 O(log ⁡ n) {\display O(\log n)}입니다.

O(logn) 상한으로 개선

${\displaystyle O(}$log ⁡ n) ${\displaystyle O(\$log n)}에서 기본 하위 변경 횟수를 제한했습니다. 따라서 각 기본 하위 변경에 비용 O(1) 상각이 있음을 보여줄 수 있다면 O(log ⁡ n) {\displaystyle O(\log n)}에서 액세스 작업을 제한할 수 있습니다. 이것은 잠재적인 방법을 사용하여 수행됩니다.

보조 트리의 v 아래에 있는 노드의 수를 s(v)라고 합니다. 그런 다음 잠재 함수 φ ∑ ⁡ v 로그 ⁡($v)$ {\$displaystyle \Phi$=\sum _{v}\log {s(v)}}가 표시됩니다. 우리는 분할의 상각된 비용은 다음과 같이 제한된다는 것을 알고 있습니다.

${\displaystyle cost(play(v))\leq 3\left(\log {s(root(v))}-\log {s(v)}\right)+1}$

우리는 splaying 후 v가 경로-부모 노드 w의 자식임을 알고 있습니다. 그래서 우리는 알고 있습니다.

${\displaystyles(v)\leqs(w)}$

우리는 이러한 불평등과 분할된 액세스 비용을 사용하여 다음과 같은 제한이 있는 텔레스코프 합계를 달성합니다.

${\displaystyle 3\left(\log {s(R)}-\log {s(v)}\right)+O({\text{선호하는 자녀 변경 수}})}$

여기서 R은 표현된 트리의 루트이며, 선호하는 자식 변경 수는 ${\displaystyle O(\log }$ ⁡ n) ${\displaystyle O(\$log n)}.s(R) = n 이므로 O(log ⁡ n) {\display O(\log n)}를 상각합니다.

어플

링크/컷 트리를 사용하여 비순환 그래프에 대한 동적 연결 문제를 해결할 수 있습니다. 두 노드 x와 y가 주어지면 FindRoot(x) = FindRoot(y)인 경우에만 연결됩니다. 같은 목적으로 사용할 수 있는 또 다른 데이터 구조는 오일러 투어 트리입니다.

최대 흐름 문제를 해결하는 데 링크/컷 트리를 사용하여 Dinic의 알고리즘 실행 시간을 $O{\displaystyle ({}^{}}$ ${\displaystyle 2^{}}$ E${\displaystyle )}$ ${\display$ O$(V^{2}E)}$에서 $O{\displaystyle (V}$ ${\displaystyle \mathrm{로그}}$ ⁡ V) ${\display O(VE\$log V)}로 향상시킬 수 있습니다.

참고 항목

• 스플레이 트리
• 전위법
• 탑트리

더보기