국소 선형화 방법

수치해석에서는 국부적 선형화(LL) 방법은 연속적인 시간 간격에서 주어진 방정식의 국부적(편파적) 선형화를 바탕으로 미분방정식에 대한 수치적 통합자를 설계하기 위한 일반적인 전략이다. 그런 다음 연속된 각 구간의 끝에서 결과물 부분적 선형 방정식의 해법으로 수치적 통합자를 반복적으로 정의한다. LL 방법은 통상, 지연, 무작위, 확률적 미분 방정식과 같은 다양한 방정식에 대해 개발되었다. LL 통합자는 (잠재적으로 시끄러운) 관측치의 시계열이 주어진 미지변수 및 미지변수 등식의 관측치 추정에 대한 추론 방법의 구현에 있어 핵심 요소다. LL 계획은 신경과학, 금융, 임업관리, 제어공학, 수학통계 등 다양한 분야에서 복잡한 모델을 다루는 이상이다.

배경

미분 방정식은 여러 현상의 시간 진화를 설명하는 중요한 수학 도구가 되었다. 예를 들어 태양 주위의 행성의 회전, 시장에서의 자산 가격의 동적, 뉴런의 불, 전염병의 전파 등이 그것이다. 단, 이러한 방정식의 정확한 해법은 일반적으로 알려져 있지 않기 때문에, 숫자 통합자에 의해 얻어지는 수치적 근사치가 필요하다. 현재 역동적 연구에 초점을 맞춘 공학 및 응용 과학 분야의 많은 응용 프로그램들은 이러한 방정식의 역학을 가능한 한 보존하는 효율적인 숫자 통합자들의 개발을 요구한다. 이러한 주된 동기로 지역 선형화 통합업체가 개발되었다.

고차 국소 선형화 방법

고차 국소 선형화(HOL) 방법은 선형 방정식의 안정성과 역학을 보존하는 미분방정식에 대한 고차 통합자를 확보하기 위한 국소 선형화 방법의 일반화다. 통합자는 두 부분으로 나누어 연속된 시간 간격으로 원래 방정식의 솔루션 x를 구한다: 국부적 선형화 방정식의 솔루션 z에 $\mathbf {r} =\mathbf {x} -\mathbf {z}$ r = $\mathbf {r} =\mathbf {x} -\mathbf {z}$ - $\mathbf {r} =\mathbf {x} -\mathbf {z}$ {\ $displaystyle \mathbf$ { $r}$ =\ $mathbf {x}$ -\ $mathbf {z$

국소 선형화 계획

국소 선형화(LL) 체계는 미분방정식의 종류에 대해 LL 또는 HOL 방법에서 도출된 분리의 수치적 구현을 허용하는 최종 재귀 알고리즘이다.

ODE에 대한 LL 방법

d차원 일반 미분 방정식(ODE) 고려

${\frac {d\mathbf {x} \left(t\right)}{dt}}=\mathbf {f} \left(t,\mathbf {x} \left(t\right)\right),\qquad t\in \left[t_{0},T\right],\qquad \qquad \qquad \qquad (4.1)$

$\mathbf {f}$ 조건 $\mathbf {x} (t_{0})=\mathbf {x} _{0}$ ( $\mathbf {x} (t_{0})=\mathbf {x} _{0}$ $\mathbf {x} (t_{0})=\mathbf {x} _{0}$ ) $\mathbf {x} (t_{0})=\mathbf {x} _{0}$ = $\mathbf {x} (t_{0})=\mathbf {x} _{0}$ 0 ${\$ 여기서 f {\ $displaystyle$ 으)는 서로 다른 함수다 $\mathbf {f}$ .

$\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ ( $\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ ) h $\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ = $\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ { $\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ : $\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ = $\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ , $\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ . $\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ . $\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ $\left(t\right)_{h}=\{t_{n}:n=0,..,N\}$ ${\displaystyle \left(t\오른쪽)$ $_{h}=\{t_{n}n=0,..,$ 그 시간 간격의 N\}}이 시간 분할[t0, T]최대stepsize h과{\displaystyle[t_{0}일 경우 ,T]}가 tn<>t n+1{\displaystyle t_{n}<, t_{n+1}}과 hnxtn에서+1− tn≤ h{\displaystyle h_{n}=t_{n+1}-t_{n}\leq h}. 그 후 그 방정식의 로컬 선형화(4.1). 그 time step ${\$ t_ ${n$ }} 상수 공식 수율의 변동 $t_{n}$

${\displaystyle \mathbf {x}(t_{n}+h)=\mathbf {x}(t_{n})+\mathbf {x}(t_{n};h)+\mathbf {r}(t_{n},\mathbf {x};h}),$

어디에

$\mathbf {\phi } (t_{n},\mathbf {z} _{n};h)=\int \limits _{0}^{h}e^{\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})(h-s)}(\mathbf {f} (t_{n},\mathbf {z} _{n})+\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})s)\,ds\qquad$

선형 근사치의 결과 및

$\mathbf {r} (t_{n},\mathbf {z} _{n};h)=\int \limits _{0}^{h}e^{\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})(h-s)}\mathbf {g} _{n}(s,\mathbf {x} (t_{n}+s))\,ds,\qquad \qquad \qquad (4.2)$

선형 근사치의 잔차. Here, $\mathbf {f} _{\mathbf {x} }$ and $\mathbf {f} _{t}$ denote the partial derivatives of f with respect to the variables x and t, respectively, and $\mathbf {g} _{n}(s,\mathbf {u} )=\mathbf {f} (s,\mathbf {u} )-\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})\mathbf {u} -\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})(s-t_{n})-\mathbf {f} (t_{n},\mathbf {z} _{n})+\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})\mathbf {z} _{n}.$ $\mathbf {g} _{n}(s,\mathbf {u} )=\mathbf {f} (s,\mathbf {u} )-\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})\mathbf {u} -\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})(s-t_{n})-\mathbf {f} (t_{n},\mathbf {z} _{n})+\mathbf {f} _{\mathbf {x} }(t_{n$ $,\mathbf {z} _{n}\mathbf {z} _{n}.$ $}$

국소 선형 디스커트화

시간 디스커트 $\left(t\right)_{h}$ ) $\left(t\right)_{h}$ ${\$ $_{h$ $t_{n+1}\in \left(t\right)_{h}$ 지점 t $t_{n+1}\in \left(t\right)_{h}$ + $t_{n+1}\in \left(t\right)_{h}$ $t_{n+1}\in \left(t\right)_{h}$ ( t $t_{n+1}\in \left(t\right)_{h}$ ) h ${\$ 에서 ODE(4.1)의 로컬 선형 디스커트화 $_{h}}$ 는 $t_{n+1}\in \left(t\right)_{h}$ 재귀적 표현으로 정의된다.

$\mathbf {z} _{n+1}=\mathbf {z} _{n},\mathbf {z} }(t_{n},\mathbf {z}),\qquad {\text{}}}}\mathb {z}={x}}\qquad \qquad \qquad \qquad (4.3)$

국소 선형 소멸(4.3)은 순서 2와 함께 비선형 ODE의 솔루션으로 수렴되지만, 선형 ODE의 솔루션과 일치한다. 재귀(4.3)는 지수 오일러 디스커트화라고도 한다.^[3]

고차 로컬 선형 디스패치

시간 디스커트화 $(t)_{h},$ ) h $(t)_{h},$ , $(t)_{h}$ 의 경우, $t_{n+1}\in (t)_{h}$ $t_{n+1}\in (t)_{h}$ t n $t_{n+1}\in (t)_{h}$ $t_{n+1}\in (t)_{h}$ ( $t_{n+1}\in (t)_{h}$ ) h {\ $displaystyle t_{n+1}\in$ (t)_ ${h}$ 에서 ODE(4.1)의 고차 로컬 선형(HOL) 디커트화는 반복 $(t)_{h},$ 표현으로 정의된다 $t_{n+1}\in (t)_{h}$ .

$\mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h_{n})+{\widetilde {\mathbf {r} }}(t_{n},\mathbf {z} _{n};h_{n}),\qquad {\text{ with }}\quad \mathbf {z} _{0}=\mathbf {x} _{0},\qquad \qquad \qquad (4.4)$

어디 r~{\displaystyle{\tilde{r}}}은 명령은 잔여 r− r~(. e., r(t, zn;h)에(t, zn;h)∝ hα+1){\displaystyle(i.e.,\left\vert \mathbf{r}(t_{n},\mathbf{z}_{n};h)-{\widetilde{\mathbf(>2)근사{\displaystyle \alpha}α. {r} $}}}}(t_{n},\mathb {z} _{n};h)\right\vert \propto h^{\ret +1}).$ $}$ HOL discretation (4.4)은 $(i.e.,\left\vert \mathbf {r} (t_{n},\mathbf {z} _{n};h)-{\widetilde {\mathbf {r} }}(t_{n},\mathbf {z} _{n};h)\right\vert \propto h^{\alpha +1}).$ 순서 $\alpha$ $\alpha$ 과 $\alpha$ (와) 융합하여 비선형 ODE의 해법으로 사용되지만, 선형 ODE의 해법과 일치한다.

HOL 분석은 두 가지 방법으로 도출될 수 있다:^[1]^[4]^[5]^[6] 1) r의 적분 표현(4.2)에 근사치를 함으로써 (양분 기반) 그리고 2) (적분자 기반)은 다음에 의해 정의된 r의 차등 표현을 위해 수치적 통합자를 사용하여 도출할 수 있다.

${\frac {d\mathbf {r} (t)}{dt}}=\mathbf {q} (t_{n},\mathbf {z} _{n};t\mathbf {,\mathbf {r} } (t)\mathbf {)} ,\qquad {\text{ with }}\qquad \mathbf {r} (t_{n})=\mathbf {0,} \qquad \qquad \qquad (4.5)$

모든 $t\in \lbrack t_{k},t_{k+1}]$ $t\in \lbrack t_{k},t_{k+1}]$ [ t $t\in \lbrack t_{k},t_{k+1}]$ $t\in \lbrack t_{k},t_{k+1}]$ k $t\in \lbrack t_{k},t_{k+1}]$ + $t\in \lbrack t_{k},t_{k+1}]$ $t\in \lbrack t_{k},t_{k+1}]$ 에 대해 $t\in \lbrack t_{k},t_{k+1}]$ \ $displaystyle t\in \lbrack t_{k},t_{k+1$ 여기서

$\mathbf {q} (t_{n},\mathbf {z} _{n};s\mathbf {,\xi } )=\mathbf {f} (s,\mathbf {z} _{n}+\mathbf {\phi } \left(t_{n},\mathbf {z} _{n};s-t_{n}\right)+\mathbf {\xi } )-\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})\mathbf {\phi } (t_{n},\mathbf {z} _{n};s-t_{n})-\mathbf {f} _{t}(t_{n},\mathbf {z} _{n})(s-t_{n})-\mathbf {f} (t_{n},\matsbf {z} _{n}).$

예를 들어 HOL 분리는 다음과 같다.

로컬 선형화된 런지 쿠타 디스커트화^[6]^[4]

$\qquad \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h_{n})+h_{n}\sum _{j=1}^{s}b_{j}\mathbf {k} _{j},\quad {\text{ with }}\quad \mathbf {k} _{i}=\mathbf {q} (t_{n},\mathbf {z} _{n};{\text{ }}t_{n}+c_{i}h_{n}\mathbf {,} \mathbf {} h_{n}\sum _{j=1}^{i-1}a_{ij}\mathbf {k} _{j}),$

which is obtained by solving (4.5) via a s-stage explicit Runge–Kutta (RK) scheme with coefficients $\mathbf {c} =\left[c_{i}\right],\mathbf {A} =\left[a_{ij}\right]\quad and\quad \mathbf {b} =\left[b_{j}\right]$ .

로컬 선형 테일러 디스커트화^[5]

\mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h_{n})+\int _{0}^{h_{n}}e^{(h_{n}-s)\mathbf {f} _{\mathbf {x} }\left(t_{n},\mathbf {z} _{n}\right)}\sum _{j=2}^{p}{\frac {\mathbf {c} _{n,j}}{j!}}s^{j}\,ds,{\text{ with }}\mathbf {c} _{n,j}=\left({\frac {d^{j+1}\mathbf {x} (t)}{dt^{j+1}}}-\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n}){\frac {d^{j}\mathbf {x} (t)}{dt^{j}}}\right)\mid _{t=\mathbf {z} _{n}},

$\mathbf {g} _{n}$ 는 주문 처리된 테일러 확장에 의해 g n {\ $displaystyle \mathbf {g} _{n}$ in $\mathbf {g} _{n}$ (4.2)의 근사치에서 비롯된다.

멀티스테프형 지수 전파 디스트리뷰트

${\textstyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h)+h\sum _{j=0}^{p-1}\gamma _{j}\nabla ^{j}\mathbf {g} _{n}(t_{n},\mathbf {z} _{n}),\quad with\quad \gamma _{j}=(-1)^{j}\int \limits _{0}^{1}e^{(1-\theta )h\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})}\left({\begin{array}{c}-\theta \\j\end{array}}\right)d\theta ,}$

which results from the interpolation of $\mathbf {g} _{n}$ in (4.2) by a polynomial of degree p on $t_{n},\ldots ,t_{n-p+1}$ , where $\nabla ^{j}\mathbf {g} _{n}(t_{m},\mathbf {z} _{m})$ denotes the j-th $\mathbf {g} _{n}(t_{m},\mathbf {z} _{m})$ $\mathbf {g} _{n}(t_{m},\mathbf {z} _{m})$ ( $\mathbf {g} _{n}(t_{m},\mathbf {z} _{m})$ $\mathbf {g} _{n}(t_{m},\mathbf {z} _{m})$ , $\mathbf {g} _{n}(t_{m},\mathbf {z} _{m})$ $\mathbf {g} _{n}(t_{m},\mathbf {z} _{m})$ ) $\mathbf {g} _{n}(t_{m},\mathbf {z$ 의 역차.

Runge Kutta 유형 지수 분포 분석 ^[7]

${\textstyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h)+h\sum _{j=0}^{p-1}\gamma _{j,p}\nabla ^{j}\mathbf {g} _{n}(t_{n},\mathbf {z} _{n}),\quad {\text{ with }}\quad \gamma _{j,p}=\int \limits _{0}^{1}e^{(1-\theta )h\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {z} _{n})}\left({\begin{array}{c}\theta p\\j\end{array}}\right)d\theta ,}$

$t_{n},\ldots ,t_{n}+(p-1)h/p$ , $t_{n},\ldots ,t_{n}+(p-1)h/p$ , $t_{n},\ldots ,t_{n}+(p-1)h/p$ , , t , $t_{n},\ldots ,t_{n}+(p-1)h/p$ + $t_{n},\ldots ,t_{n}+(p-1)h/p$ ( $t_{n},\ldots ,t_{n}+(p-1)h/p$ - $t_{n},\ldots ,t_{n}+(p-1)h/p$ ) $t_{n},\ldots ,t_{n}+(p-1)h/p$ 의 $t_{n},\ldots ,t_{n}+(p-1)h/p$ 다항식 p에 의한 g $\mathbf {g} _{n}$ , $,$ $t_{n},\ldots ,t_{n}+(p-1)h/p$ t , t , t , t , t + ( $t_{n},\ldots ,t_{n}+(p-1)h/p$ ) h $t_{n},\ldots ,t_{n}+(p-1)h/p$ / p {\ $displaystyle t_{n},\dots$ ,t_ ${n$ $}+($ p-1) $h/p}$ 의 $\mathbf {g} _{n}$ 보간에서 비롯된다 $t_{n},\ldots ,t_{n}+(p-1)h/p$

선형화된 지수 애덤스 디스트리뷰트^[8]

${\textstyle \mathbf {z} _{n+1}=\mathbf {z} _{n}+\mathbf {\phi } (t_{n},\mathbf {z} _{n};h)+h\sum _{j=1}^{p-1}\sum _{l=1}^{j}{\frac {\gamma _{j+1}}{l}}\nabla ^{l}\mathbf {g} _{n}(t_{n},\mathbf {z} _{n}),\quad {\text{ with }}\quad \gamma _{j+1}=(-1)^{j+1}\int \limits _{0}^{1}e^{(1-\theta )h\mathbf {f} _{\mathbf {x} }\left(t_{n},\mathbf {z} _{n}\right)}\\theta \left \pretted\j\end{array}{c}-\theta \\data}d\theta ,}$

$t_{n},\ldots ,t_{n-p+1}$ 는 t $t_{n},\ldots ,t_{n-p+1}$ $t_{n},\ldots ,t_{n-p+1}$ $t_{n},\ldots ,t_{n-p+1}$ - $t_{n},\ldots ,t_{n-p+1}$ + $t_{n},\ldots ,t_{n-p+1}$ {\ $displaystyle$ $t_$ ${n}, t_{n$ $},$ t_{n-p $+1$ }의 $\mathbf {g} _{n}$ 헤르미트 다항식 p에 $\mathbf {g} _{n}$ g $\mathbf {g} _{n}$ {\ $displaystyle$ $t_{n-p+$ 1}의 보간에서 비롯된다 $t_{n},\ldots ,t_{n-p+1}$

로컬 선형화 방식

All numerical implementation $\mathbf {y} _{n}$ of the LL (or of a HOLL) discretization $\mathbf {z} _{n}$ involves approximations ${\widetilde {\phi }}_{j}$ to integrals $\phi _{j}$ of the form

$\phi_{j}(\mathbf {A} ,h)=\int \{0}^{h}e^{h-s)\mathbf {A}}s^{j-1}\,ds,\qquad j=1,2\ldots,$

여기서 A는 d × d 행렬이다. 모든 $\mathbf {z} _{n}$ 순서의 LL(또는 $\mathbf {z} _{n}$ ) $\mathbf {z} _{n}$ 의 $\mathbf {y} _{n}$ { $\mathbf {y} _{n}$ ${\$ $displaystyle \mathbf$ $\mathbf {y} _{n}$ { $y} _{n$ $}$ _ ${$ n $}$ 숫자 구현을 일반적으로 Local Linearization schempt라고 한다.^[1]^[9]

매트릭스 지수화 관련 통합 계산

통합 계산을 위한 여러 알고리즘 $\phi _{j}$ $\phi _{j}$ ${\$ 중에서 지수 매트릭스에 대한 합리적인 Padé 및 Krylov 하위 공간 근사치를 기반으로 하는 알고리즘이 선호된다 $\phi _{j}$ 이를 위해 중심적인 역할이 표현으로^[10]^[5]^[11] 작용하고 있다.

$\sum \nolimits _{i=1}^{l}\phi_{i}(\mathbf {A}, h)\mathbf {a} _{i}=\mathbf {L} e^{h\mathbf {H}}\mathbf {r},},},}}}$

$\mathbf {a} _{i}$ 서 $\mathbf {a} _{i}$ ${\$ 는 $\mathbf{a}_i$ d-차원 벡터,

${\displaystyle \mathbf{H}={\begin{bmatrix}\mathbf{A}&\mathbf{v}_{나는}&,\mathbf{v}_{l-1}&, \cdots, \mathbf{v}_{1}\\\mathbf{0}및 &, \mathbf{0}&1&, \cdots &, 0\\\mathbf{0}&\mathbf{0}&0&, \ddots, 0\\\vdots, \vdots & &, \vdots &, \ddots & &, 1\\\mathbf{0}&\mathbf{0}&0&, \cdots &, 0\.End{bmatrix}}}\mathbb{R}^{(d+l)\times(d+l)}, \in.$

$\mathbf {L} =[\mathbf {I} \quad \mathbf {0} _{d\times l}]$ , $\mathbf {r} =[\mathbf {0} _{1\times (d+l-1)}\quad 1]^{\intercal },$ $\mathbf {v} _{i}=\mathbf {a} _{i}(i-1)!$ , being $\mathbf {I}$ ${\$ d차원 $\mathbf {I}$ ID 매트릭스 $.$

If $\mathbf {P} _{p,q}(2^{-k}\mathbf {H} h)$ denotes the (p; q)-Padé approximation of $e^{2^{-k}\mathbf {H} h}$ and k is the smallest natural number such that ${\displaystyle 2^{-k}\mathbf {H} h \leq$ ${\frac {1}{1}:{2}}, 그러면}$

$\left\vert \sum \nolimits _{i=1}^{l}\phi _{i}(\mathbf {A} ,h)\mathbf {a} _{i}-\mathbf {L} \left(\mathbf {\mathbf {P} } _{p,q}(2^{-k}\mathbf {H} h)\right)^{2^{k}}\mathbf {r} \right\vert \varpropto h^{p+q+1}.$

If $\mathbf {\mathbf {k} } _{m,k}^{p,q}(h,\mathbf {H} ,\mathbf {r} )$ denotes the (m; p; q; k) Krylov-Padé approximation of $e^{h\mathbf {H} }\mathbf {r}$ , then ^[12]

$\left\vert \sum \nolimits _{i=1}^{l}\phi _{i}(\mathbf {A} ,h)\mathbf {a} _{i}-\mathbf {L\mathbf {k} } _{m,k}^{p,q}(h,\mathbf {H} ,\mathbf {r} )\right\vert \varpropto h^{\min({m,p+q+1})},$

여기서 $m\leq d$ $m\leq d$ $m\leq d$ $m\leq d$ 은 $m\leq d$ (는) 크릴로프 하위 공간의 치수다.

주문-2 LL 방식

$\mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L}(\mathbf {P}) _{p,q}(2^{-k_{n}}}\mathbf {M} _{n}))^{2^{k_{n}}}\mathbf {r,}$ ^[13]^[9] $\displaystyle \qquad \qquad (4.6)}$

여기서 행렬 $\mathbf {M} _{n}$ $\mathbf {M} _{n}$ ${\$ L 및 r은 다음과 같이 정의된다.

$\mathbf {M} _{n}={\begin{bmatrix}\mathbf {f} _{\mathbf {x} }(t_{n},\mathbf {y} _{n})&\mathbf {f} _{t}(t_{n},\mathbf {y} _{n})&\mathbf {f} (t_{n},\mathbf {y} _{n})\\0&0&1\\0&0&0\end{bmatrix}}\in \mathbb {R} ^{(d+2)\times (d+2)},$

L=}과 r⊺)[01×(d+1)1]{\displaystyle \mathbf{r}^ᆮ=\left[{\begin{배열}{2}\mathbf{0}_{1\times(d+1)}&1\end{배열}}\right]}과{L\displaystyle \mathbf{}=\left[{\begin{배열}{2}\mathbf{나는}&\mathbf{0}_{2}\end{배열}d\times}\right][0×12002d]. p+ $p+q>1$ > $p+q>1$ $[\displaystyle p+q]1}.$ ODE의 대형 시스템용

$\mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L\mathbf {k} } _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {M} _{n},\mathbf {r} )\mathbf {,} \qquad {\text{ with }}\qquad m_{n}>2.$

주문-3 LL-테일러 방식

$\mathbf {y} _{n+1}=\mathbf {y} _{n}\mathbf {L} _{1}(\mathbf {P}) _{p,q}(2^{-k_}}}\mathbf {T} _{n}) _{n}^{2^{k_{n}}}\mathbf {r} _{1}\mathbf {,}$ ^[5] $\displaystyle \qquad \qquad (4.7)}$

여기서 자율 ODE의 경우 행렬 T $\mathbf {T} _{n},\mathbf {L} _{1}$ L $\mathbf {T} _{n},\mathbf {L} _{1}$ ${\$ } 및 $\mathbf {T} _{n},\mathbf {L} _{1}$ r $\mathbf {r} _{1}$ ${\$ }은 $($ 으)로 정의된다 $\mathbf {r} _{1}$ .

$\mathbf{T}_{n}=\left는 경우에는{\begin{배열}{cccc}\mathbf{f}_{\mathbf{)}}(\mathbf{y}_{n})&,(\mathbf{나는}\mathbf{f}^{\intercal}({y}\mathbf_{n\otimes}))\mathbf{f}_{\mathbf{xx}}{f}(\mathbf{y}_{n})&(\mathbf{y}_{n})\mathbf, \mathbf{0}&\mathbf{f}(\mathbf{y}_{n})\\0&, 0&, 0&, 0\\0&, 0&, 0&, 1\\0&.;0&, 0&, 0\end{배열}}\right]\in \mathbb{R} ^{(d+3)\reason (d+3)},$

L1-1ndr1⊺)[01×(d+2=1]{L\displaystyle \mathbf{}_ᆭ=\left[{\begin{배열}{2}\mathbf{나는}&\mathbf{0}_{d\times 3}\end{배열}}\right]\quad and\quad\mathbf{r}_ᆯ^ᆰ=\left[{\begin{배열}{2}\mathbf{0}_{1\times(d+2)}&1\end{배열}}\right]}[0d×12003]. . 여기서 $\mathbf {f} _{\mathbf {xx} }$ $\mathbf {f} _{\mathbf {xx} }$ ${\$ 은 x와 p + q > 2에 관한 f의 두 번째 파생물을 나타낸다 $\mathbf {f} _{\mathbf {xx} }$ . 대규모 ODE 시스템인 경우

$\mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {L\mathbf {k} } _{m_{n},k_{n}}^{p,q}(h_{n},\mathbf {T} _{n},\mathbf {r} )\mathbf {,} \qquad {\text{ with }}\qquad m_{n}>3.$

주문-4 LL-RK 체계

$\mathbf {y} _{n+1}=\mathbf {y} _{n}{4} _{n}+{h_{n}}}{6}}}}{2\mathbf {k} _{3}+}\mathbf{4}}}}}}}\mathbp}}}}}}}}}}}}}}}}\mathbf\mathbf\mathbf}}}}}}}}}}}}}}}}}}}$ ^[4] ^[6] $\displaystyle \qquad \qquad (4.8)}$

어디에

$\mathbf {u} _{j}=\mathbf {P}(\mathbf {L}){p,q}(2^{-\kappa _{j}\mathbf {M} _{n}c_{j}h_{n}})^{2^{\kappa _{j}}\mathbf {r}$

그리고

$\mathbf {k} _{j}=\mathbf {f} \left(t_{n}+c_{j}h_{n},\mathbf {y} _{n}+\mathbf {u} _{j}+c_{j}h_{n}\mathbf {k} _{j-1}\right)-\mathbf {f} \left(t_{n},\mathbf {y} _{n}\right)-\mathbf {f} _{\mathbf {x} }\left(t_{n},\mathbf {y} _{n}\right)\mathbf {u} _{j}\ -\mathbf {f} _{t}\left(t_{n},\mathbf {y} _{n}\right)c_{j}h_{n},$

with $\mathbf {k} _{1}\equiv \mathbf {0} ,c=\left[{\begin{array}{cccc}0&{\frac {1}{2}}&{\frac {1}{2}}&1\end{array}}\right],$ and p + q > 3. For large systems of ODEs, the vector $\mathbf {u} _{j}$ in the above scheme is replaced by $\mathbf {u} _{j}=\mathbf {L\mathbf {k} } _{m_{j},k_{j}}^{p,q}(c_{j}h_{n},\mathbf {M} _{n},\mathbf {r} )$ with $m_{j}>4.$ ${\displaystyle m_{j}>4.$ $}$

도만드와 프린스의 지역 선형화된 룬지-쿠타 체계

$\mathbf {y} _{n+1}=\mathbf {y} _{n}+\mathbf {u} _{s}+h_{n}\sum _{j=1}^{s}b_{j}\mathbf {k} _{j}\qquad {\text{ and }}\qquad {\widehat {\mathbf {y} }}_{n+1}=\mathbf {y} _{n}+\mathbf {u} _{s}+h_{n}\sum _{j=1}^{s}{\widehat {b}}_{j}\mathbf {k} _{j},\quad$ ^[14] ^[15] $\displaystyle \qquad \qquad (4.9)}$

여기서 s = 7은 단계 수입니다.

$\mathbf {k} _{j}=\mathbf {f(} t_{n}+c_{j}h_{n},\mathbf {y} _{n}+\mathbf {u} _{j}+h_{n}\sum _{i=1}^{s-1}a_{j,i}\mathbf {k} _{i})-\mathbf {f} \left(t_{n},\mathbf {y} _{n}\right)-\mathbf {f} _{\mathbf {x} }\left(t_{n},\mathbf {y} _{n}\right)\mathbf {u} _{j}\ -\mathbf {f} _{t}\left(t_{n},\mathbf {y} _{n}\right)c_{j}h_{n},$

with $\mathbf {k} _{1}\equiv \mathbf {0}$ , and $a_{j,i},b_{j},{\widehat {b}}_{j}\quad and\quad c_{j}$ are the Runge–Kutta coefficients of Dormand and Prince and p + q > 4. 위의 구성표에서 $\mathbf {u} _{j}$ 벡터 $\mathbf {u} _{j}$ $\mathbf {u} _{j}$ ${\$ 는 각각 ODE의 소형 또는 대형 시스템에 대한 Padé 또는 Krylor-Padé 근사치로 계산된다.

안정성과 역동성

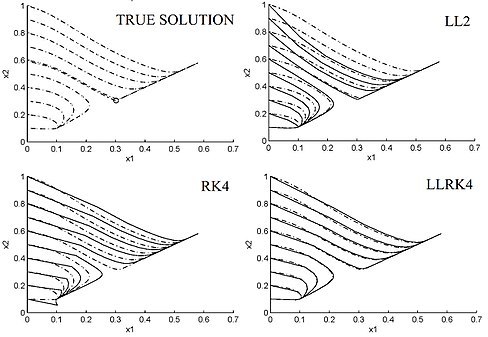
Fig. 1 Phase portrait (dashed line) and approximate phase portrait (solid line) of the nonlinear ODE (4.10)-(4.11) computed by the order-2 LL scheme (4.2), the order-4 classical Rugen-Kutta scheme RK4, and the order-4 LLRK4 schemes (4.8) with step size h=1/2 , and p=q=6.

건설에 의해 LL과 HOL 탈바꿈은 선형 ODE의 안정성과 역학을 계승하지만, 일반적으로 LL 체계의 경우는 아니다. $p\leq q\leq p+2$ $p\leq q\leq p+2$ $p\leq q\leq p+2$ q $p\leq q\leq p+2$ + $p\leq q\leq p+2$ ${\displaystyle p\leq q\leq p+2$ }을 $p\leq q\leq p+2$ 를) 사용할 경우 LL 스키마(4.6)-(4.9)는 A-안정적이다.^[4] q = p + 1 또는 q = p + 2를 사용할 경우 LL 체계(4.6)–(4.9)도 L-안정화된다.^[4] 선형 ODE의 경우, LL 체계(4.6)-(4.9)는 순서 p + q로 수렴한다.^[4]^[9] 또한, p = q = $m_{n}$ 과 m ${\$ = d로, 위에서 설명한 모든 LL 체계는 현재 개인용 컴퓨터에서 선형 ODE의 ″exact 연산(이동점 산술의 정밀도까지)에 산출된다.^[4]^[9] 여기에는 경직 및 고진동 선형 방정식이 포함된다. 더욱이 LL 체계 (4.6)-(4.9)는 선형 ODE에 대해 규칙적이며 해밀턴 조화 진동자의 동조 구조를 계승한다.^[5]^[13] 이러한 LL 계획은 또한 선형화로서 쌍곡선 평형점과 동일한 단계화를 갖는 다른 수치 체계들이 갖는 주기적 궤도를 중심으로 안정적이고 불안정한 다지관의 보다 나은 재현을 보여준다.^[5]^[13] 예를 들어 그림 1은 ODE의 위상 초상화를 보여준다.

{\begin{aligned}&{\frac {dx_{1}}{dt}}=-2x_{1}+x_{2}+1-\mu f(x_{1},\lambda )\qquad \qquad (4.10)\\[6pt]&{\frac {dx_{2}}{dt}}=x_{1}-2x_{2}+1-\mu f(x_{2},\lambda )\qquad \qquad \quad (4.11)\end{aligned}}

$f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}$ ( $f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}$ , $f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}$ ) = $f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}$ ( $f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}$ + $f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}$ + $f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}$ $f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}$ 2 $f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}$ ) - $f(u,\lambda )=u(1+u+\lambda u^{2})^{-1}$ ${\$ 1+ $u+\dada u^{2}^,$ $\mu =15$ = $\mu =15$ ${\displaystyle$ $\$ $mu =15$ $\lambda =57$ = $\lambda =57$ ${\displaystyda$ = $57$ 그 근사치를 다양한 방법으로 구한다. 이 시스템에는 $0\leq x_{1},x_{2}\leq 1$ $0\leq x_{1},x_{2}\leq 1$ , x $0\leq x_{1},x_{2}\leq 1$ { $0\leq x_{1},x_{2}\leq 1$ $0\leq x_{1}, x_{2}\leq 1$ 지역에 2개의 안정적인 정지 지점과 1개의 불안정한 정지 지점이 있다 $0\leq x_{1},x_{2}\leq 1$

DDE에 대한 LL 방법

d차원 지연 미분 방정식(DDE) 고려

${\frac {d\mathbf {x} (t)}{dt}}=\mathbf {f} (t,\mathbf {x} (t),\mathbf {x} _{t}(-\tau _{1}),\ldots ,\mathbf {x} _{t}(-\tau _{m})),\qquad t\in [t_{0},T],\qquad \qquad (5.1)$

으로 m일정 지연 τ 나는입니다.;0{\displaystyle \tau_{나는}>. 0}일 경우와 초기 조건)t 0(s))φ(s){\displaystyle \mathbf{)}_{t_{0}모든 그것을}(s)=\mathbf{\varphi}(s)}∈[− τ, 0], f는 미분 가능 함수{\displaystyle s\in[-\tau ,0],}, 음 t:[− τ, 0]⟶ R., {\dis $playstyle \mathbf {x} _{t}:[-\tau ,0]\longrightarrow \mathb {R}$ ^{ $d}}}}$ 은 $\mathbf {x} _{t}:[-\tau ,0]\longrightarrow \mathbb {R} ^{d}$ (는) 다음과 같이 정의된 세그먼트 함수다.

$\mathbf {x} _{t}s:=\mathbf {x}(t+s),{\text{}s\in [-\tau ,0],$

for all $t\in [t_{0},T],\mathbf {\varphi } :[-\tau ,0]\longrightarrow \mathbb {R} ^{d}$ is a given function, and ${\displaystyle \tau =\max \left\{\tau _{1},\ldots ,\tau _{m}\right\}.$ $}$