무임계 끈 이론에서의 로렌츠 불변성

Lorentz invariance in non-critical string theory

보통 비임계 [1]문자열 이론은 폴랴코프가 제안한 접근법 프레임에서 고려됩니다.다른 접근방식은 [2][3][4]에서 개발되었습니다.그것은 양자상대론 이론에서 명시적인 로렌츠 불변성을 유지하는 보편적인 방법을 나타냅니다.4차원 민코프스키 시공간에서의 남부-고토 끈 이론의 예에서 이 아이디어는 다음과 같이 설명될 수 있다.

광원뿔 게이지
시간처럼 생긴 롤리치의 게이지.
표준 변환.
대칭을 측정하다.
스핀 질량 스펙트럼.[4]로렌츠 불변 광원뿔 게이지는 DDF 벡터장의 특이점과 관련이 있습니다.
스핀 질량 스펙트럼.[5]제한된 등급의 끈 운동은 축 대칭을 가진 월드 시트에 대응하는 것으로 간주됩니다.로렌츠 불변 광원뿔 게이지는 대칭축과 관련이 있다.
스핀 질량 스펙트럼.[3]로렌츠 불변 Rohrlich의 게이지는 세계 시트의 주기와 관련이 있다.
광중간자의 실험적 스핀 질량 스펙트럼은 현 [6][7]모델 예측과 중첩된다.

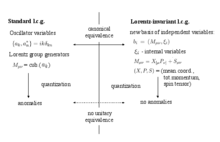
기하학적으로 세계 문자열 시트는 특정 매개 변수화 또는 게이지를 고정하기 위해 평행 평면 시스템에 의해 슬라이스됩니다.평면은 게이지 축인 정규 벡터μ n으로 정의됩니다.이 벡터가 광원추에 속한다면 파라메이션은 광원추 게이지에 해당하고, 월드 시트의 주기μ P를 따라 방향지어지면 Rohrlich의 게이지와 같은 시간적 특성을 가집니다.표준 광원뿔 게이지의 문제는 벡터μ n이 일정하고(예μ: n = (1, 1, 0, 0)), 평면의 시스템은 민코프스키 시공간에서 "변형"이라는 것이다.로렌츠 변환은 이러한 고정 평면에 대한 월드 시트의 위치를 바꾸고, 그 후에 월드 시트의 재자변화가 뒤따른다.양자 수준에서, 리파라메트리제이션 그룹은 로렌츠 그룹에서도 나타나며 이론의 로렌츠 불변성에 위배되는 변칙을 가지고 있다.한편, Rohrlich의 게이지는 세계 시트 자체와 관련이 있습니다μ.그 결과 로렌츠 발생기는 재매개 없이 n과 월드시트를 동시에 변환한다μ.끈 이론에서 사용할 수 있는 P개의 다른 동적 벡터에 추가하여μ 빛과 같은 축μ n을 월드 시트와 관련짓는 경우에도 동일한 특성이 유지됩니다.이러한 방법으로 로렌츠 그룹은 3차적으로 작용하고 양자 이상을 가지지 않는 세계 시트의 로렌츠 불변 매개변수화를 구성합니다.

대수적으로 이것은 새로운 변수 집합에 대한 고전 역학의 표준 변환 ai -> b에i 해당하며, 모든 필요한 대칭 생성자를 명시적으로 포함한다.표준 광원뿔 게이지의 경우, 로렌츠 발생기μν M은 발진기i 변수 a의 관점에서 입방체이며, 그 양자화는 잘 알려진 이상을 획득합니다.Lorentz group generators와 내부변수 θ를i 포함하는 집합i b = (Mi,120)를μν 가정하여 M을 전체 위상공간에 보완한다μν.이러한 세트를 선택할 때, will는i M이 있는 단순한μν 포아송 괄호를 가지도록 주의해야 한다.그러한 변수의 국지적 존재는 다르부스의 정리에 의해 제공된다.새로운 변수 집합의 양자화는 로렌츠 군에서 이상을 제거한다.규범적으로 동등한 고전 이론은 단일 동등한 양자 이론과 반드시 일치하는 것은 아니며, 그렇기 때문에 양자 이상은 한 가지 접근법에는 존재하고 다른 접근법에는 존재하지 않을 수 있습니다.

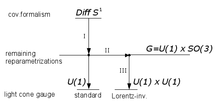
군이론 끈이론은 게이지 대칭 Diff1 S, 원의 재자극화를 가진다.대칭은 Virasoro 대수n L에 의해 생성됩니다. 표준 광원뿔 게이지는 게이지 자유도의 대부분을 고정하고 사소한 위상 회전 U(1) ~ S만1 남습니다.그것들은 해밀턴 L에0 의해 생성된 주기적인 문자열 진화에 대응한다.이 다이어그램에 추가 레이어: 고정 월드 시트에 대한 질량 중심 프레임의 게이지 축 회전 및 단순한 진화 계수를 포함한 월드 시트의 게이지 변환 그룹 G = U(1) x SO(3)를 소개합니다.표준 광원뿔 게이지는 SO(3) 인자의 한 점 선택에 해당하므로 로렌츠 비불변 파라미터화가 발생합니다.따라서 G의 게이지 궤도에서 다른 대표자를 선택해야 하며, 이번에는 로렌츠 불변 방식으로 월드 시트와 관련된다.이 대표적인 변칙 게이지로 역학을 축소한 후에는 자유도가 이론에서 제거됩니다.게이지 축의 방향을 보존하는 회전과 진화를 포함한 단순한 게이지 대칭 U(1) x U(1)가 남습니다.

이 프로그램의 정상적인 실장은 [3][4][5]에서 실시되고 있습니다.이것은 양자 개방 난부-고토 끈 이론의 몇 가지 동일하지 않은 단일 버전으로, 게이지 축이 세계 시트의 다른 기하학적 특징에 부착되어 있습니다.이들의 공통 특성은 다음과 같습니다.

  • d=4에서의 명시적 로렌츠 불변성
  • 게이지에 의해 고정된 재자극 자유도
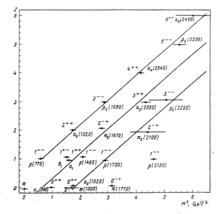
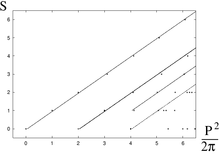
  • 레지 유사 스핀 질량 스펙트럼

현대 끈 이론에서 공존하는 다양한 분기에 익숙한 독자들은 왜 많은 다른 양자 이론이 본질적으로 동일한 물리적 시스템에 대해 구성될 수 있는지 궁금해하지 않을 것이다.여기서 설명하는 접근방식은 독자적인 궁극적인 결과를 낳는 것이 아니라, 독자적인 양자 끈 이론의 구축에 적합한 일련의 도구를 제공할 뿐입니다.모든 차원 값, 특히 d=4를 사용할 수 있기 때문에 응용 프로그램이 더 현실적일 수 있습니다.예를 들어, 이 접근방식은 강입자의 스펙트럼과 전자기 [6][7]상호작용을 설명하기 위해 강입자의 물리학에 적용될 수 있다.

레퍼런스

  1. ^ 폴라프, A.M. (1981)"보닉 문자열의 양자 기하학"물리학 글자 B.다른 V.2103(, )는 207-0693-1693(81)90743-0693(81)90743-0693-0693-1693(81)90743-0ISN 0370-2693.: 본 논문은 선형 오실로스코프의 집합에서 양자남부 문자열 이론과 같은 선형 오실로스코프의 수집에 대한 선형 오실로스코프가 포함되어 있으며, 다른 가치 이론과 같은 비선형 오실로스코프의 다른 값도 있다.양자화 Dirac의 연산자 형식주의를 위해 아래에 인용된 논문.
  2. ^ Rohrlich, F. (1975-03-31). "Quantum Dynamics of the Relativistic String". Physical Review Letters. American Physical Society (APS). 34 (13): 842–845. doi:10.1103/physrevlett.34.842. ISSN 0031-9007.
  3. ^ a b c Pron'ko, G.P. (1990). "Hamiltonian theory of the relativistic string". Reviews in Mathematical Physics. World Scientific Pub Co Pte Lt. 02 (3): 355–398. doi:10.1142/s0129055x90000119. ISSN 0129-055X.
  4. ^ a b c S.V. Klimenko, I.N. Nikitin, Non-Critical String Theory: 고전적 및 양자적 측면, Nova Science Pub., New York 2006, ISBN 1-59454-267-8.
  5. ^ a b 수학과 물리학의 초대칭 및 비대칭 구조 간결한 백과사전, 엔트리 "Anomaly-Free Subsets", Kluwer Academic Publishers, Dordrecht 2003, ISBN 1-4020-1338-8.
  6. ^ a b Berdnikov, E. B.; Nanobashvili, G. G.; Pron'Ko, G. P. (1993-06-10). "The relativistic theory for principal trajectories and electromagnetic transitions of light mesons part I". International Journal of Modern Physics A. World Scientific Pub Co Pte Lt. 08 (14): 2447–2464. doi:10.1142/s0217751x93000965. ISSN 0217-751X.
  7. ^ a b Berdnikov, E. B.; Nanobashvili, G. G.; Pron'Ko, G. P. (1993-06-20). "The relativistic theory for principal trajectories and electromagnetic transitions of light mesons part II". International Journal of Modern Physics A. World Scientific Pub Co Pte Lt. 08 (15): 2551–2567. doi:10.1142/s0217751x93001016. ISSN 0217-751X.

「 」를 참조해 주세요.

다음 문자열 이론 교재에서는 임계 차원 이외의 문자열의 이상 없는 양자화 가능성에 대해 언급하고 있습니다.

  • L. 브링크, M.Heneaux, 끈 이론의 원리, 플레넘 프레스, 뉴욕과 런던, (1988), 페이지 157

다른 표현을 사용하지 않는 경우

중앙 충전을 피하기 위해 현악기 연산자를 사용할 수 있습니까?다시, 그러한 표현을 구성하는 것이 매우 잘 가능할 수 있으며, 만약 그렇다면, 결과 양자 이론은 여기에서 설명되는 것과 매우 다를 수 있습니다.아직 구축되지 않은 이 이론은 (예를 들어, 로렌츠 대수의 무한 차원 표현의 발생을 통해) 고유의 관심을 가질 수 있다.게다가, 이 이론은 발진기 변수의 사용에 기초하지 않기 때문에, 막과 같은 고차원 물체로 더 쉽게 확장될 수 있습니다.

또한 페이지 157~159에서는 임의의 짝수 차원으로 비라소로 대수의 이상을 가지지 않는 비진동자 표현 클래스의 닫힌 끈 이론의 양자해를 명시적으로 제시한다.

  • B.M. Barbashov, V.V. Nesterenko, 상대론적 끈이론 입문, 싱가포르, 세계과학, (90), 페이지 64:

그렇게 철저하게 공부한 사람이라는 것은 이해하기 어렵다.

끈이 사실적인 4차원 시공간에서 양자 수준에서 일관되게 분석될 수 없기 때문에 고전 이론과 비상대론적 양자 역학에서 물체.상기의 곤란에 직면하지 않는 상대론적 문자열 문제에 대한 다른 양자 해법을 찾기 위한 시도가 이루어졌다.

또한 11항과 30항에서는 Rohrlich와 Polyakov에 의한 접근 프레임에 있어서의 비임계 끈 이론의 양자화가 기술되어 있다.

  • M. Green, J. Schwarz, E. Witten, 초끈 이론 제1권, 케임브리지 대학교.프레스, (1987), 페이지 124:

경로 적분에서의 컨포멀 팩터 θ의 기여도를 고려하면 다음과 같이 나타납니다.

적분(3.1.13)은 물리적으로 다음과 같이 생각할 수 있다.

sense(sense)는 θ 의존성이 취소되지 않는 경우에도 유효합니다.이 가능성은 매우 기발한 제안의 동기를 부여했지만 여전히 불확실합니다.어떤 경우에도 슈퍼스트링 통일에서는 임계치수를 벗어나는 방법에 대한 대부분의 제안에서는 임계치수에 존재하는 무질량 입자를 잃을 것으로 예상되기 때문에 δ의존성이 취소되는 임계치수가 바람직하다.

주의: 이것은 모든 결합 상태가 거대한 하드론의 물리학에서 중요하지 않은 끈 이론의 사용을 배제하지 않습니다.여기서는 이론의 자기 일관성, 특히 로렌츠 불변성만 필요하다.