자기 구조
Magnetic structure물질의 자기 구조라는 용어는 일반적으로 순서가 정해진 결정 격자 안에 순서가 정해진 자기 스핀 배열과 관련이 있다. 그것의 연구는 고체 물리학 분야다.
자기 구조
대부분의 고체 물질은 비자기적, 즉 자기 구조를 나타내지 않는다. 파울리 배타 원리로 인해 각 상태는 반대 스핀의 전자가 차지하기 때문에 어디에서나 전하 밀도가 보상되고 자유도의 회전 정도는 사소한 것이다. 그러나 그러한 물질은 일반적으로 Pauli 파라마그네틱스나 Langevin 또는 Landau 직경 등으로 인해 약한 자기 행동을 보인다.
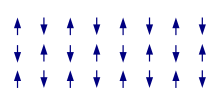
더 흥미로운 경우는 물질의 전자가 위에서 언급한 대칭 위에서 저절로 깨지는 경우다. 지상 상태의 강자성에는 공통의 스핀 정량화 축과 주어진 스핀 양자수의 전자가 전지구적으로 과잉되어 있으며, 다른 방향보다 한 방향을 가리키는 전자가 더 많아 거시적 자기화가 가능하다(일반적으로, 대부분의 전자는 위쪽을 가리키기 위해 선택된다). 가장 간단한(협착형) 항암자기술의 경우 여전히 일반적인 정량화 축이 존재하지만 전자 스핀들이 위아래를 번갈아 가리키고 있어 다시 거시적 자기화 취소로 이어지고 있다. 그러나, 특히 상호작용의 좌절의 경우, 결과 구조는 훨씬 더 복잡해질 수 있으며, 국소 스핀의 본질적으로 3차원 방향이다. 마지막으로, 자석에 의해 프로토타입적으로 나타나는 철자성은 어떤 의미에서 중간적인 경우인데, 여기서 자석은 철자학에서와 같이 전체적으로 강화되지 않지만 국소 자석은 다른 방향을 가리킨다.
위의 논의는 지상 국가 구조와 관련이 있다. 물론, 유한한 온도는 스핀 구성을 생략하게 한다. 여기서 두 가지 극단적인 관점을 대조할 수 있다: 자성의 스토너 그림(일행 자력이라고도 함)에서는 전자 상태가 소산되며, 이들의 평균 영역 상호작용은 대칭 파괴로 이어진다. 이러한 관점에서, 온도가 증가하면 국소 자기화는 단일 탈색 전자가 상향 채널에서 하향 채널로 이동함에 따라 균일하게 감소할 것이다. 한편, 국지적인 순간의 경우, 전자 상태는 특정 원자로 국부화되어 원자 스핀을 제공하며, 원자 스핀은 단거리에서만 상호작용하며 일반적으로 하이젠베르크 모델과 함께 분석된다. 여기서, 유한한 온도는 이상적인 구성으로부터 원자 회전 방향의 편차를 유도하므로, 페로마그네틱의 경우 거시적 자기화도 감소시킨다.
국부적인 자성의 경우, 많은 자기 구조를 자기 공간 그룹에 의해 설명할 수 있으며, 이것은 3차원 결정에서 위/아래 구성의 가능한 모든 대칭 그룹에 대한 정확한 설명을 제공한다. 그러나 이러한 형식주의는 헬리마그네틱스에서 발견되는 것과 같은 좀 더 복잡한 자기 구조를 설명할 수 없다.
그것들을 연구하기 위한 기술들
이러한 순서는 온도 및/또는 적용된 자기장의 크기 함수로서의 자기 민감성을 관찰함으로써 연구될 수 있지만, 스핀들의 배열의 진정한 3차원 그림은 중성자 회절을 통해 가장 잘 얻어진다.[1][2] 중성자는 주로 구조 내 원자의 핵에 의해 산란된다. 그러므로 물질이 파라마그네틱으로 작용하는 자성모멘트의 순서점 위의 온도에서 중성자 회절은 결정학적 구조의 그림만을 제공할 것이다. 명령점 이하에서는, 예를 들어, 중성자가 스스로 스핀을 가지고 있기 때문에 자석 모멘트로부터 산란되는 것을 경험하게 된다. 그러므로 Bragg 반사의 강도는 바뀔 것이다. 실제로 어떤 경우에는 순서의 단위 셀이 결정학적 구조보다 크면 완전히 새로운 Bragg-Reflection이 발생할 것이다. 이것은 상부 구조 형성의 한 형태다. 따라서 전체 구조물의 대칭은 결정학적 하부 구조와 다를 수 있다. 비자기적 우주군 중 하나가 아니라 1651개 자성(슈브니코프) 그룹 중 하나로 설명할 필요가 있다.[3]
일반적인 X선 회절은 스핀들의 배열에는 '맹목'이지만, 자기 구조를 연구하기 위해 X선 회절의 특별한 형태를 사용하는 것이 가능해졌다. 물질에 포함된 원소 중 하나의 흡수 에지에 가까운 파장을 선택하면 산란이 변칙적으로 되고 산란에 대한 이 성분은 (어느 정도) 원자의 외전자의 비구형 모양에 (무엇인가) 민감하게 된다. 이것은 이러한 유형의 변칙적인 X선 회절에는 원하는 유형의 정보가 포함되어 있음을 의미한다.
최근에는 중성자나 싱크로트론 선원에 의지하지 않고 자기 구조를 연구할 수 있는 테이블탑 기법이 개발되고 있다.[4]
화학 원소의 자기 구조
상온과 압력에서 강자성인 원소는 철분, 코발트, 니켈 세 가지뿐이다. 이들의 퀴리 온도인 Tc가 실온(Tc > 298K)보다 높기 때문이다. 가돌리늄은 상온(293K) 바로 밑의 자발적 자성을 가지며, 때로는 네 번째 강자성 원소로 계산되기도 한다. 가돌리늄이 헬리마그네틱 순서를 가지고 있다는 제안이 있었지만,[5] 다른 이들은 가돌리늄이 전통적인 페로마그네틱이라는 오랜 관점을 옹호한다.[6]
디즈프로시움과 에르비움 원소는 각각 두 개의 자기 전환이 있다. 상온에서는 파라마그네틱이지만, 각각의 네엘 온도 이하에서는 헬마그네틱이 되고, 이후 퀴리 온도 이하에서는 강자극이 된다. 홀뮴, 테르비움, 툴륨 원소는 더욱 복잡한 자기 구조를 보여준다.[7]
네엘 온도 이상으로 흐트러지는 반자성 순서도 있다. 크롬은 다소 단순한 항암소자 같지만 단순 업다운 스핀 교대 위에 비혼합성 스핀밀도파 변조도 있다.[8] 망간(α-Mn 형태)은 29개의 원자 단위 셀을 가지고 있어, 복잡하지만 저온(자성 우주군 P42'm')[9][10]에서 반감되는 항초자성 배열로 이어진다. 전자로 인해 자성을 띠는 대부분의 원소와 달리 구리와 은의 자성 순서는 훨씬 약한 핵자기 모멘트(비교 보어 자석 및 핵 자석)에 의해 절대 영도에 가까운 전환 온도로 이어진다.[11][12]
초전도체가 되는 원소들은 임계 온도 이하의 초다이아마그네틱을 보인다.
| 아니요. | 이름 | 초전도c T | 퀴리 온도 | 네엘 온도 |
|---|---|---|---|---|
| 3 | 리튬 | 0.0004 K[13] | ||
| 13 | 알루미늄 | 1.18K[13] | ||
| 22 | 티타늄 | 0.5K[13] | ||
| 23 | 바나듐 | 5.4 K[13] | ||
| 24 | 크롬 | 311 K[14] | ||
| 25 | 망간 | 100K[14] | ||
| 26 | 철 | 1044 K[15] | ||
| 27 | 코발트 | 1390 K[15] | ||
| 28 | 니켈 | 630K[15] | ||
| 29 | 구리 | 6 * 10K−8[14] | ||
| 30 | 아연 | 0.85 K[13] | ||
| 31 | 갈륨 | 1.08 K[13] | ||
| 40 | 지르코늄 | 0.6K[13] | ||
| 41 | 니오비움 | 9.25 K[13] | ||
| 42 | 몰리브덴 | 0.92 K[13] | ||
| 43 | 테크네튬 | 8.2 K[13] | ||
| 44 | 루테늄 | 0.5K[13] | ||
| 45 | 로듐 | 0.0003 K[13] | ||
| 46 | 팔라듐 | 1.4K[13] | ||
| 47 | 은색 | 5.6 * 10K−10[14] | ||
| 48 | 카드뮴 | 0.52K[13] | ||
| 49 | 인듐 | 3.4K[13] | ||
| 50 | 주석 | 3.7 K[13] | ||
| 57 | 란타넘 | 6K[13] | ||
| 58 | 세륨 | 13K[14] | ||
| 59 | 프라세오디뮴 | 25K[14] | ||
| 60 | 네오디뮴 | 19.9 K[14] | ||
| 62 | 사마륨 | 13.3 K[14] | ||
| 63 | 유로피움 | 91 K[14] | ||
| 64 | 가돌리늄 | 293.4 K[15] | ||
| 65 | 테르비움 | 221K[15] | 230K[14] | |
| 66 | 디스프로슘 | 92.1 K[15] | 180.2 K[14] | |
| 67 | 홀뮴 | 20K[15] | 132.2 K[14] | |
| 68 | 에르비움 | 18.74 K[15] | 85.7 K[14] | |
| 69 | 툴륨 | 32K[15] | 56K[14] | |
| 71 | 루테튬 | 0.1K[13] | ||
| 72 | 하프늄 | 0.38K[13] | ||
| 73 | 탄탈룸 | 4.4 K[13] | ||
| 74 | 텅스텐 | 0.01 K[13] | ||
| 75 | 레늄 | 1.7K[13] | ||
| 76 | 오스뮴 | 0.7K[13] | ||
| 77 | 이리듐 | 0.1K[13] | ||
| 80 | 수성. | 4.15 K[13] | ||
| 81 | 탈륨 | 2.4K[13] | ||
| 82 | 이끌다 | 7.2 K[13] | ||
| 90 | 토륨 | 1.4K[13] | ||
| 91 | 프로텍티늄 | 1.4K[13] | ||
| 92 | 우라늄 | 1.3K[13] | ||
| 95 | 아메리슘 | 1K[13] |
참조
- ^ 자성 물질의 중성자 회절 / Yu. A. Izyumov, V.E. Naish, R.P. Ozerov ; 요아힘 부치너가 러시아어로 번역했다. 뉴욕 : 상담국, c1991. ISBN030611030X
- ^ 브라이언 토비의 데모
- ^ Kim, Shoon K. (1999). Group theoretical methods and applications to molecules and crystals (digitally print. 1. paperback version ed.). Cambridge, U.K.: Cambridge University Press. p. 428. ISBN 9780521640626.
- ^ Mei, Antonio B.; Gray, Isaiah; Tang, Yongjian; Schubert, Jürgen; Werder, Don; Bartell, Jason; Ralph, Daniel C.; Fuchs, Gregory D.; Schlom, Darrell G. (2020). "Local Photothermal Control of Phase Transitions for On-Demand Room-Temperature Rewritable Magnetic Patterning". Advanced Materials. 32 (22): 2001080. arXiv:1906.07239. doi:10.1002/adma.202001080. ISSN 1521-4095.
- ^ Coey, J.M.D.; Skumryev, V.; Gallagher, K. (1999). "Is gadolinium really ferromagnetic?". Nature. Springer Science and Business Media LLC. 401 (6748): 35–36. doi:10.1038/43363. ISSN 0028-0836.
- ^ Kaul, S. N. (2003). "Is gadolinium a helical antiferromagnet or a collinear ferromagnet?". Pramana. Springer Science and Business Media LLC. 60 (3): 505–511. doi:10.1007/bf02706157. ISSN 0304-4289.
- ^ Jensen, Jens; Mackintosh, Allan (1991). Rare Earth Magnetism: Structures and Excitations (PDF). Oxford: Clarendon Press. Retrieved 2020-08-09.
- ^ Marcus, P M; Qiu, S-L; Moruzzi, V L (1998-07-27). "The mechanism of antiferromagnetism in chromium". Journal of Physics: Condensed Matter. IOP Publishing. 10 (29): 6541–6552. doi:10.1088/0953-8984/10/29/014. ISSN 0953-8984.
- ^ Lawson, A. C.; Larson, Allen C.; Aronson, M. C.; Johnson, S.; Fisk, Z.; Canfield, P. C.; Thompson, J. D.; Von Dreele, R. B. (1994-11-15). "Magnetic and crystallographic order in α‐manganese". Journal of Applied Physics. AIP Publishing. 76 (10): 7049–7051. doi:10.1063/1.358024. ISSN 0021-8979.
- ^ Yamada, Takemi; Kunitomi, Nobuhiko; Nakai, Yutaka; E. Cox, D.; Shirane, G. (1970-03-15). "Magnetic Structure of α-Mn". Journal of the Physical Society of Japan. Physical Society of Japan. 28 (3): 615–627. doi:10.1143/jpsj.28.615. ISSN 0031-9015.
- ^ Huiku, M.T. (1984). "Nuclear magnetism in copper at nanokelvin temperatures and in low external magnetic fields". Physica B+C. Elsevier BV. 126 (1–3): 51–61. doi:10.1016/0378-4363(84)90145-1. ISSN 0378-4363.
- ^ Hakonen, P J (1993-01-01). "Nuclear magnetic ordering in silver at positive and negative spin temperatures". Physica Scripta. IOP Publishing. T49A: 327–332. doi:10.1088/0031-8949/1993/t49a/057. ISSN 0031-8949.
- ^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae G.W. Webb, F. Marsiglio, J.E. Hirsch (2015). "Superconductivity in the elements, alloys and simple compounds". Physica C: Superconductivity and Its Applications. 514: 17–27. arXiv:1502.04724. Bibcode:2015PhyC..514...17W. doi:10.1016/j.physc.2015.02.037.
{{cite journal}}: CS1 maint : 복수이름 : 작성자 목록(링크) - ^ a b c d e f g h i j k l m n "Elements handbook: Neel point". Retrieved 27 Sep 2018.
- ^ a b c d e f g h i "Elements handbook: Curie point". Retrieved 27 Sep 2018.