노턴 정리
Norton's theorem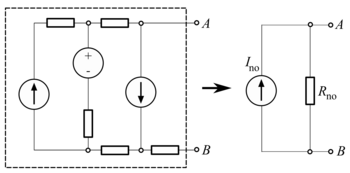
직류 회로 이론에서, 메이어-노튼 정리라고도 불리는 노턴의 정리는 선형 시간 불변 저항, 전압원 및 전류원으로 구성된 네트워크에 적용될 수 있는 단순화입니다.네트워크의 한 쌍의 단자에서 병렬로 전류원과 단일 저항으로 대체할 수 있습니다.
교류(AC) 시스템의 경우 정리는 저항뿐만 아니라 반응 임피던스에도 적용될 수 있습니다.
Norton 등가회로는 특정 주파수에서 선형 소스 및 임피던스 네트워크를 나타내기 위해 사용됩니다.
노턴의 정리와 그 쌍대인 테베냉의 정리는 회로 분석의 단순화와 회로의 초기 조건 및 정상 상태 응답을 연구하는 데 널리 사용됩니다.
노턴의 정리는 1926년 Siemens & Halske 연구원 Hans Perdinand Mayer (1895–1980)와 Bell Labs 엔지니어 Edward Lawry Norton (1898–1983)[1][2][3][4][5][6]에 의해 독립적으로 도출되었다.
Norton 전류no I은 단자에서 단락 회로로 흐르는 전류로 계산됩니다(A와 B 사이의 저항 없음).이게no 저예요.Norton 저항no R은 단자에 아무런 저항도 연결하지 않은 상태에서 생성된 출력 전압을 계산하여 구할 수 있습니다. 이는 모든 (독립) 전압원이 단락된 상태에서 단자 간의 저항입니다.이는 테베닌 저항을 계산하는 것과 동일합니다.
- 종속 소스가 있는 경우 보다 일반적인 방법을 사용해야 합니다.단자의 전압은 단자에 1A 테스트 전류를 주입하기 위해 계산됩니다.이 전압을 1A 전류로 나눈 값이 Norton 임피던스no R입니다.이 방법은 회로에 종속 소스가 포함되어 있는 경우 사용해야 하지만 종속 소스가 없는 경우에도 모든 경우에 사용할 수 있습니다.
Norton 등가 회로의 예
이 예에서 I의 총 전류는total 다음과 같습니다.
부하를 통과하는 전류는 전류 분배 규칙을 사용하여 다음과 같습니다.
![{\displaystyle {\begin{aligned}I_{\mathrm {no} }&={1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega \over 1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega +1\,\mathrm {k} \Omega }\cdot I_{\mathrm {total} }\\[5pt]&=2/3\cdot 5.625\,\mathrm {mA} =3.75\,\mathrm {mA} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6401d8ddf361d0de7567c3581cf46d6937b14d9a)
회로를 되돌아보는 등가 저항은 다음과 같습니다.
따라서 등가 회로는 2kΩ 저항과 병렬로 3.75mA 전류 소스입니다.
테베닌 환산
Norton 등가회로는 다음 식에 의해 Tévenin 등가회로에 관련지어집니다.
![{\displaystyle {\begin{aligned}&R_{\rm {th}}=R_{\rm {no}}\\[8pt]&V_{\rm {th}}=I_{\rm {no}}R_{\rm {no}}\\[8pt]&{\frac {V_{\rm {th}}}{R_{\rm {th}}}}=I_{\rm {no}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5de3a14a1c09b01ae4a7941d18fc0f4f4230b08)
큐잉 이론
큐잉 이론에서 "노튼의 정리"에 해당하는 수동 회로를 챈디 허조그 우 [3][4][7]정리라고 합니다.리버서블 큐잉시스템에서는 큐의 중요하지 않은 서브셋을 적절하게 선택된 서비스 [8]레이트로 단일(FCFS 또는 PS) 큐로 대체할 수 있습니다.
「 」를 참조해 주세요.
레퍼런스
- ^ Mayer, Hans Ferdinand (1926). "Ueber das Ersatzschema der Verstärkerröhre" [On equivalent circuits for electronic amplifiers]. Telegraphen- und Fernsprech-Technik (in German). 15: 335–337.
- ^ Norton, Edward Lawry (1926). "Design of finite networks for uniform frequency characteristic". Bell Laboratories. Technical Report TM26–0–1860.
{{cite journal}}:Cite 저널 요구 사항journal=(도움말) - ^ a b Johnson, Don H. (2003). "Origins of the equivalent circuit concept: the voltage-source equivalent" (PDF). Proceedings of the IEEE. 91 (4): 636–640. doi:10.1109/JPROC.2003.811716. hdl:1911/19968.
- ^ a b Johnson, Don H. (2003). "Origins of the equivalent circuit concept: the current-source equivalent" (PDF). Proceedings of the IEEE. 91 (5): 817–821. doi:10.1109/JPROC.2003.811795.
- ^ Brittain, James E. (March 1990). "Thevenin's theorem". IEEE Spectrum. 27 (3): 42. doi:10.1109/6.48845. S2CID 2279777. Retrieved 2013-02-01.
- ^ Dorf, Richard C.; Svoboda, James A. (2010). "Chapter 5: Circuit Theorems". Introduction to Electric Circuits (8th ed.). Hoboken, NJ, USA: John Wiley & Sons. pp. 162–207. ISBN 978-0-470-52157-1. Archived from the original on 2012-04-30. Retrieved 2018-12-08.
- ^ Gunther, Neil J. (2004). Analyzing Computer System Performance with Perl::PDQ (Online ed.). Berlin: Springer Science+Business Media. p. 281. ISBN 978-3-540-20865-5.
- ^ Chandy, Kanianthra Mani; Herzog, Ulrich; Woo, Lin S. (January 1975). "Parametric Analysis of Queuing Networks". IBM Journal of Research and Development. 19 (1): 36–42. doi:10.1147/rd.191.0036.
외부 링크
위키미디어 커먼스의 노턴 정리 관련 매체- allaboutcircuits.com의 Norton's 정리
