광학 알고리즘

시리즈의 일부
기계 학습 및 데이터 마이닝
문제 분류 클러스터링 회귀 이상 검출 데이터 클리닝 자동 ML 어소시에이션 규칙 강화 학습 구조화된 예측 기능 엔지니어링 기능 학습 온라인 학습 준지도 학습 비지도 학습 순위 매기기 학습 문법 유도
지도 학습 (분류 • 회귀) 의사결정 트리 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형 회귀 네이비 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 관련 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k자형 기대 최대화(EM) DBSCAN 광학 평균 이동
치수 축소 인자 분석 CCA ICA LDA NMF PCA PGD t-SNE
구조화된 예측 그래픽 모델 베이즈 네트 조건부 랜덤 필드 히든 마르코프
이상 검출 k-NN 국소 특이치 계수
인공신경망 자동 인코더 인지 컴퓨팅 딥 러닝 딥 드림 다층 퍼셉트론 RNN LSTM GRU ESN 저장고 계산 제한 볼츠만 기계 GAN somerset. 컨볼루션 뉴럴 네트워크 유넷 트랜스포머 비전. 스파이킹 뉴럴 네트워크 메모리 트랜지스터 전기화학 RAM(ECRAM)
강화 학습 Q-러닝 사사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 액티브 러닝 크라우드 소싱 휴먼 인 더 루프
모델 진단 학습 곡선
이론. 커널 머신 바이어스-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오컴 러닝 PAC 학습 통계학 학습 VC 이론
기계학습장 NeurolIPS ICML ML JMLR ArXiv:cs.LG
관련 기사 인공지능 용어집 기계 학습 연구를 위한 데이터 세트 목록 기계학습의 개요
v t

군집화 구조(Optics)를 식별하기 위한 점 순서 지정은 공간 데이터에서 밀도^[1] 기반 군집을 찾기 위한 알고리즘입니다.미할 앙커스트, 마르쿠스 M. 브뢰니그, 한스 피터 크리겔, 외르크 ^[2]샌더가 발표했다.기본 개념은 ^[3]DBSCAN과 유사하지만 DBSCAN의 주요 약점 중 하나인 다양한 밀도의 데이터에서 의미 있는 클러스터를 탐지하는 문제를 해결합니다.이를 위해 데이터베이스의 포인트는 공간적으로 가장 가까운 포인트가 순서에서 네이버가 되도록 (선형적으로) 정렬됩니다.또한 두 점이 동일한 군집에 속하도록 군집에 대해 허용해야 하는 밀도를 나타내는 각 점에 대해 특별한 거리가 저장됩니다.이것은 덴드로그램으로 표시됩니다.

기본 아이디어

DBSCAN과 마찬가지로 Optics에는 고려해야 할 최대 거리(반경)를 나타내는 ,과 클러스터 형성에 필요한 포인트 수를 나타내는 MinPts라는2개의 파라미터가 필요합니다.포인트 p는 적어도 MinPts 포인트가 그 $)\style$ N_${\varepsilon$}($p)}($포인트 p 자체를 포함) 내에 있는 경우 핵심 포인트이다.DBSCAN과 달리 Optics는 보다 조밀하게 패킹된 클러스터의 일부인 점을 고려하므로 각 점에는 MinPtsth 가장 가까운 점까지의 거리를 나타내는 코어 거리가 할당됩니다.

${\displaystyle {core-dist}_{\mathit {varepsilon, MinPts}}(p)=begin {case}{\text{\text}UNDEFINED}&{\text{if}} N_{\varepsilon }(p) <{\mathit {MinPts}}\{\mathit {MinPts}}{\text {-}{\varepsilon }(p)&{\text{\text{\ts}}}}}{\cases}}}}$

p 지점으로부터의 다른 지점 o의 도달 가능성 거리는 o와 p 사이의 거리 또는 p의 코어 거리 중 더 큰 것입니다.

${\displaystyle {reachability-dist}_{\mathit {\varepsilon, MinPts}}(o,p)=begin {case}{\text{\text}UNDEFINED}&{\text{if}} N_{\varepsilon }(p) <{\mathit {MinPts}}\\max({\text {core-dist}}_{\mathit {varepsilon, MinPts}}(p), {\ts}(p,o)})&{\text{cases}}\end{case}}$

p와 o가 가장 가까운 네이버일경우 p와 $o$가 같은 클러스터에 속한다고 가정해야 합니다$.$

충분히 고밀도 클러스터(w.r.t. ")를 사용할 수 없는 경우 코어 거리와 도달 가능성 거리는 모두 정의되지 않습니다.충분히 큰 ,을 지정하면 이 문제는 발생하지 않지만 모든 -근처 쿼리는 데이터베이스 전체를 반환하고 결과적으로${\displaystyle }$O ( ${\displaystyle {n\mathrm{}}^{}}$2$$) \ $displaystyle$O ( $n^$ {2$$} )런타임이 $발생$합니다.따라서 더 이상 대상이 되지 않는 클러스터의 밀도를 차단하고 알고리즘을 고속화하기 위해서는 δ 파라미터가 필요합니다.

파라미터 is은 엄밀히 말하면 필수가 아닙니다.이는 단순히 가능한 최대값으로 설정할 수 있습니다.그러나 공간 지수를 사용할 수 있는 경우에는 복잡성과 관련하여 실질적인 역할을 한다.Optics는 이 파라미터를 삭제함으로써 DBSCAN에서 추출합니다.최소한 최대값만 제시하면 됩니다.

유사 코드

Optics의 기본적인 접근법은 DBSCAN과 비슷하지만 지금까지 한 세트로 처리되지 않은 클러스터 멤버를 유지하는 대신 priority 큐(인덱스된 힙 사용 등)로 유지됩니다.

Optics(DB, eps, MinPts) 함수는 DB do p.reachability-distance = DB do N = 처리되지 않은 각 지점 p에 대해 정의되지 않음 = getNeighbors(p, eps)는 코어 거리(p, eps, MinPts)의 경우 p를 순서 목록에 처리된 출력 p로 표시합니다. 그러면 우선 순위가 정의되지 않음 =시드 내의 각 다음 q에 대한 업데이트(N, p, 시드, eps, MinPts)가 N' = getNeighbors(q, eps)를 순서 목록에 대해 처리된 출력 q로 표시합니다. core-distance(q, eps, MinPts)!= UNDEFINDINED do update(N', q, 시드, 시드, eps, MinPts, MinPts)의 경우

업데이트()에서는 priority 큐 Seeds가 p$\displaystyle$p$\$$neighborhood$ 및 q$\displaystyle$q로 각각$$$갱신$됩니다.

함수 업데이트(N, p, Seeds, eps, MinPts)는 N의 각 o에 대해 코어리스트 = 코어디스턴스(p, eps, MinPts)이며, o가 처리되지 않으면 new-reach-dist = max(coredist, dist(p,o)이며, o.reachability == 정의되지 않으면 // o가 시드디스턴스에 없습니다.Seeds.insert(o, new-reach-dist) other // o Seeds에서 new-reach-dist < o.reachability-dist then o.reachability-dist = new-reach-dist Seeds.move-up(o, new-reach-reach-dist)인 경우 개선 여부를 확인합니다.

따라서 Optics는 가장 작은 도달 가능 거리로 주석을 단 특정 순서로 포인트를 출력합니다(원래 알고리즘에서는 코어 거리도 내보냅니다만, 이것은 이후의 처리에는 필요 없습니다).

클러스터 추출

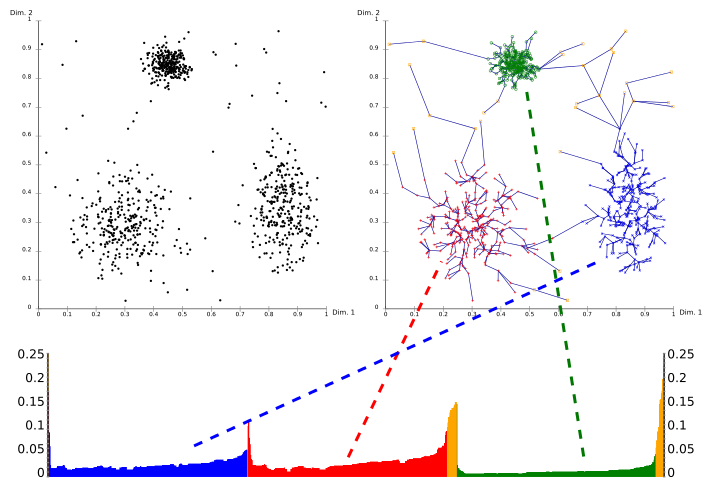
도달 가능성 그림(덴드로그램의 특수한 종류)을 사용하면 클러스터의 계층 구조를 쉽게 얻을 수 있습니다.X축은 Optics가 처리한 점의 순서와 Y축은 도달 가능 거리를 갖는 2D 그림입니다.군집에 속하는 점들은 가장 가까운 이웃에 대한 도달 가능 거리가 낮기 때문에 군집은 도달 가능성 그림에서 계곡으로 표시됩니다.계곡이 깊을수록 군집은 더 빽빽하다.

위의 그림은 이 개념을 나타내고 있습니다.왼쪽 상단 영역에 합성 예제 데이터 세트가 표시됩니다.오른쪽 상단에는 Optics에 의해 생성된 스패닝트리가 표시되며 하단에는 Optics에 의해 계산된 도달 가능성 그림이 표시됩니다.이 그림의 색상은 레이블이며 알고리즘에 의해 계산되지 않지만 그림의 계곡이 위의 데이터 집합의 군집과 어떻게 대응하는지 잘 알 수 있습니다.이 이미지의 노란색 점은 노이즈로 간주되며 도달 가능성 그림에는 계곡이 없습니다.계층적 결과의 "모든 데이터" 클러스터를 제외하고 일반적으로 클러스터에 할당되지 않습니다.

이 플롯에서 클러스터를 추출하려면 육안 검사 후 X 축의 범위를 선택하거나 Y 축의 임계값을 선택하여 수동으로 수행하거나(그 후 $결과$는 ${\$ { $displaystyle \varepsilon }$ 및$$ minPts 파라미터가 동일한 DBSCAN 클러스터링 결과와 유사합니다. 여기서 0.1의 값은 양호한 결과를 산출할 수 있습니다).경사도, 무릎 감지 또는 국소 최대치로 계곡을 탐지하는 알고리즘입니다.이러한 방법으로 얻은 클러스터링은 일반적으로 계층형이며 DBSCAN을 한 번 실행하는 것으로는 달성할 수 없습니다.

복잡성

DBSCAN과 마찬가지로 Optics는 각 포인트를 1회 처리하고 이 처리 $중에1개$의$$\$displaystyle \varepsilon }$ - neighborhood$$ 쿼리를 수행합니다.O${\displaystyle }$( ${\displaystyle \log n}$n$$) \ $displaystyle$ O ( \ $log$n )$$runtime $o$ o o given given given given ${\displaystyle \mathrm{given}}$ ${\displaystyle \mathrm{given}}$ given given given${\displaystyle }$given given${\displaystyle }$、 O ( n$$\ $cdot$\ $log$n )의 $전체{\displaystyle }$ runtime을 얻을 수 있습니다.원본 Optics 논문의 저자들은 DBSCAN에 비해 실제 일정 속도 저하 계수가 1.6이라고 보고했습니다.$값$이 너무 크면 네이버쿼리 비용이 선형 복잡해질 수 있으므로 알고리즘 비용에 큰 영향을 미칠 수 있습니다$.$

x , d ( ,) \ $displaystyle$\ $varepsilon$> \ $max$_ {$x$ ,$y$ } $d ( x$ ,$y$ ) } (데이터 세트의 최대 거리보다 큼)를 선택하는 것은 가능하지만 모든 네이버 쿼리가 완전한 데이터 세트를 반환하기 때문에 2차 복잡성으로 이어집니다.공간 인덱스를 사용할 수 없는 경우에도 힙 관리에 추가 비용이 발생합니다.$따라서{\displaystyle }$ 데이터셋에는 $§\displaystyle\varepsilon$을 적절하게$$ 선택해야 합니다.

내선번호

Optics-OF는^[4] Optics에 기반한 이상치 검출 알고리즘입니다.주요 용도는 다른 특이치 검출 방법을 사용하는 것에 비해 낮은 비용으로 Optics의 기존 실행에서 특이치를 추출하는 것이다.보다 잘 알려진 버전의 LOF는 같은 개념에 기초하고 있습니다.

DeLi-Clu,^[5] Density-Link-Clustering은 단일 링크 클러스터링과 Optics의 아이디어를 결합하여 ${\$ \ $displaystyle$\ $varepsilon }$ $파라미터$를 삭제하고 Optics보다 성능을 향상시킵니다.

HiSC는^[6] Optics에 기반한 계층형 서브스페이스 클러스터링(축-병렬) 방식입니다.

HiCO는^[7] Optics에 기반한 계층형 상관 클러스터링 알고리즘입니다.

DiSH는^[8] 보다 복잡한 계층을 찾을 수 있는 HiSC보다 향상된 기능입니다.

FOPTICS는^[9] 랜덤 투영을 사용하여 보다 신속하게 구현됩니다.

HDBSCAN*^[10]은 DBSCAN의 미세화에 기초하고 있습니다.클러스터에서 경계점을 제외하기 때문에 Hartigan에 ^[11]의한 밀도 수준의 기본 정의를 엄밀하게 따릅니다.

유용성

Optics, Optics-OF, DeLi-Clu, HiSC, HiCO 및 DiSH의 Java 구현은 ELKI 데이터 마이닝 프레임워크에서 사용할 수 있습니다(여러 거리 함수에 대한 인덱스 가속과 δ 추출 방법을 사용한 자동 클러스터 추출).기타 Java 구현에는 Weka 확장 기능이 포함되어 있습니다(클러스터 추출은 지원되지 않습니다).

R 패키지 "dbscan"에는 유클리드 거리에 대해서만 인덱스 가속을 위해 k-d 트리를 사용하는 Optics(기존 dbscan 유사 및 δ 클러스터 추출 모두 포함)의 C++ 구현이 포함되어 있다.

PyClustering 라이브러리 및 skit-learn에서 Optics의 Python 구현을 이용할 수 있습니다.HDBSCAN*은 hdbscan 라이브러리에서 사용할 수 있습니다.

레퍼런스