비지도 학습

시리즈의 일부
기계 학습 및 데이터 마이닝
문제 분류 클러스터링 회귀 이상 검출 데이터 클리닝 자동 ML 어소시에이션 규칙 강화 학습 구조화된 예측 기능 엔지니어링 기능 학습 온라인 학습 준지도 학습 비지도 학습 순위 매기기 학습 문법 유도
지도 학습 (분류 • 회귀) 의사결정 트리 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형 회귀 네이비 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 관련 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k자형 기대 최대화(EM) DBSCAN 광학 평균 이동
치수 축소 인자 분석 CCA ICA LDA NMF PCA PGD t-SNE
구조화된 예측 그래픽 모델 베이즈 네트 조건부 랜덤 필드 히든 마르코프
이상 검출 k-NN 국소 특이치 계수
인공신경망 자동 인코더 인지 컴퓨팅 딥 러닝 딥 드림 다층 퍼셉트론 RNN LSTM GRU ESN 저장고 계산 제한 볼츠만 기계 GAN somerset. 컨볼루션 뉴럴 네트워크 유넷 트랜스포머 비전. 스파이킹 뉴럴 네트워크 메모리 트랜지스터 전기화학 RAM(ECRAM)
강화 학습 Q-러닝 사사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 액티브 러닝 크라우드 소싱 휴먼 인 더 루프
모델 진단 학습 곡선
이론. 커널 머신 바이어스-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오컴 러닝 PAC 학습 통계학 학습 VC 이론
기계학습장 NeurolIPS ICML ML JMLR ArXiv:cs.LG
관련 기사 인공지능 용어집 기계 학습 연구를 위한 데이터 세트 목록 기계학습의 개요
v t

비지도 학습은 태그 없는 데이터에서 패턴을 학습하는 알고리즘의 한 종류입니다.인간의 중요한 학습 수단인 모방으로 인해 기계는 세상의 컴팩트한 내부 표현을 만들고 상상력이 풍부한 콘텐츠를 만들어 낼 수 있기를 바랍니다.전문가에 의해 데이터가 태그되는 감독 학습과 달리, 예를 들어 "공" 또는 "물고기"로 비감독 방법은 패턴을 확률 밀도 또는 신경 특징 선호의 조합으로 포착하는 자기 구성을 나타낸다.감독 스펙트럼의 다른 수준은 기계가 지침으로 수치 성능 점수만 제공하는 강화 학습과 데이터의 더 작은 부분에 태그를 다는 반감독 학습이다.

비지도 학습의 두 가지 광범위한 방법은 신경 네트워크와 확률론적 방법이다.

뉴럴 네트워크

태스크 대 메서드

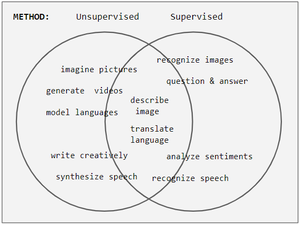
뉴럴 네트워크 태스크는 종종 차별적(인식) 또는 생성적(상상)으로 분류됩니다.항상은 아니지만 종종 차별적 작업은 감독된 방법을 사용하고 생성 작업은 감독되지 않은 방법을 사용한다(벤 다이어그램 참조). 그러나 분리는 매우 모호하다.예를 들어 객체 인식은 지도 학습을 선호하지만 비지도 학습은 객체를 그룹으로 묶을 수도 있습니다.또한 진행이 진행됨에 따라 일부 태스크는 두 가지 방법을 모두 사용하고 일부 태스크는 다른 태스크에서 전환됩니다.예를 들어, 이미지 인식은 엄격한 지도 하에 시작되었지만, 감독되지 않은 사전 훈련을 채택함으로써 하이브리드가 되었고, 중퇴, 재교육 및 적응 학습률이 등장하면서 다시 감독 쪽으로 이동했다.

트레이닝

학습 단계 동안, 비감독 네트워크는 주어진 데이터를 모방하려고 시도하고 모방된 출력의 오류를 사용하여 스스로를 수정합니다(즉, 가중치와 편견을 보정).이것은 아이들이 언어를 배울 때의 모방 행동과 유사하다.이 에러는, 잘못된 출력이 발생할 가능성이 낮은 것, 또는 네트워크내의 불안정한 고에너지 상태로 표시되는 경우가 있습니다.

역전파를 주로 사용하는 감독 방법과는 달리, 비감독 학습은 다음을 포함한 다른 방법도 사용한다.홉필드 학습 규칙, 볼츠만 학습 규칙, 대조적 발산, 웨이크 슬립, 변동 추론, 최대 가능성, 최대 A 후향성, 깁스 샘플링 및 역전파 재구성 오류 또는 숨겨진 상태 재파라미터화.자세한 내용은 아래 표를 참조하십시오.

에너지

에너지 함수는 네트워크의 활성화 상태를 거시적으로 측정하는 것입니다.Boltzmann 기계에서는 비용 함수의 역할을 합니다.이 물리학과의 유추는 입자의 움직임 pθ$(\displaystyle\propto }$ e의$$^E/kT 미시적 확률에서 기체의 거시적 에너지를 분석한 루드비히 볼츠만에서 영감을 얻었다.여기서 k는 볼츠만 상수, T는 온도이다.RBM 네트워크에서의 관계는 p^−E = e / ^[2]Z 입니다.여기서 p&E는 가능한 모든 활성화 패턴에 따라 달라집니다.Z $={\displaystyle \underset{}{}}$ ${\displaystyle \underset{}{a}}$ A ${\displaystyle \underset{}{l}}$ ${\displaystyle \underset{}{P}}$ ${\displaystyle \underset{}{t}}$ ${\displaystyle \underset{}{t}}$ e ${\displaystyle \underset{}{r}}$ ${\displaystyle \underset{}{n}}$s \ $displaystyle \sum$ _ { $All$ Patterns$}$ e$$. 보다 정확하게 말하면, p(a) = e^-E(a)/Z는 숨겨진 모든 뉴런의 활성화 패턴입니다.따라서 초기 신경망은 볼츠만 기계라는 이름을 가지고 있다.폴 스몰렌스키는 E를 하모니라고 부른다.네트워크는 낮은 에너지, 즉 높은 조화를 추구합니다.

네트워크

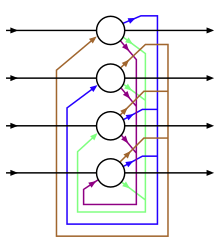
이 표는 다양한 비감독 네트워크의 접속도를 나타내고 있습니다.상세한 것에 대해서는, 「네트워크의 비교」섹션에 기재되어 있습니다.원은 뉴런이고 그 사이의 가장자리는 연결 무게입니다.네트워크 설계가 변경됨에 따라 새로운 기능을 활성화하기 위해 기능이 추가되거나 더 빨리 학습할 수 있도록 기능이 제거됩니다.예를 들어, 뉴런은 강력한 출력을 허용하기 위해 결정론적(홉필드)과 확률론적(볼츠만) 사이에서 변화하고, 학습을 촉진하기 위해 계층(RBM) 내에서 가중치가 제거되거나, 연결이 비대칭(헬름홀츠)이 되도록 허용된다.

홉필드	볼츠만	RBM	적층 볼츠만	헬름홀츠	자동 인코더	VAE
자기 연결 레이어가 1개인 철로 된 자기 도메인을 기반으로 하는 네트워크.컨텐츠 주소 지정 가능한 메모리로 사용할 수 있습니다.	네트워크는 2개의 레이어(숨겨진 레이어와 가시 레이어)로 구분되지만 대칭형 2방향 가중치를 사용합니다.볼츠만의 열역학에 이어, 개인의 확률은 거시적인 에너지를 발생시킨다.	제한된 볼츠만 기계.이것은 Boltzmann 기계로, 분석을 다루기 쉽게 하기 위해 층 내 횡방향 연결이 금지되어 있습니다.	이 네트워크에는 숨겨진 기능의 계층을 인코딩하기 위한 여러 RBM이 있습니다.1개의 RBM이 훈련되면 다른 파란색 숨김 레이어(왼쪽 RBM 참조)가 추가되어 상위2개의 레이어가 빨간색 및 파란색 RBM으로 훈련됩니다.따라서 RBM의 중간 레이어는 훈련 단계에 따라 숨김 또는 가시적인 역할을 합니다.	적층된 Boltzmann 기계의 양방향 대칭 연결 대신 루프를 형성하기 위한 별도의 단방향 연결부가 있습니다.그것은 세대 차별을 모두 한다.	입력 세계의 적절한 중간 레이어 표현을 찾는 것을 목적으로 하는 피드 포워드 네트워크.이 네트워크는 결정론적이기 때문에 후속 VAE만큼 견고하지 않습니다.	자동 인코더에 변동 추론을 적용합니다.중간 레이어는 가우스 분포의 평균과 분산 세트입니다.확률적 특성은 결정론적 자동 인코더보다 더 강력한 상상력을 허용합니다.

사람들의 이름이 새겨진 네트워크 중 홉필드만이 신경 네트워크와 직접 협력했습니다.볼츠만과 헬름홀츠는 인공신경망보다 먼저 나왔지만, 물리학과 생리학에서의 그들의 연구는 사용된 분석 방법에 영감을 주었다.

역사

1969	Minsky & Papert의 Perceptrons는 숨겨진 레이어가 없는 Perceptron이 XOR에서 실패했음을 나타냅니다.
1970년대	(개산일) AI winter I
1974	WA Little이 인지를 위해 제안한 이싱 자기 모델
1980	후쿠시마는 나중에 컨볼루션 뉴럴 네트워크라고 불리는 네오인지트론을 도입한다.주로 SL에서 사용되지만 여기서 언급할 필요가 있습니다.
1982	존 홉필드에 의해 CAM 및 분류자로 기술된 배리언트홉필드 네트
1983	Sherington & Kirkpatrick의 1975년 연구에 이어 Hinton & Sejnowski에 의해 기술된 확률론적 뉴런을 가진 이징 변종 볼츠만 기계.
1986	Paul Smolensky는 실질적으로 동일한 볼츠만 에너지 함수를 가진 RBM인 Harmony Theory를 발표했다.Smolensky는 실용적인 훈련 계획을 주지 않았다.힌튼은 2000년대 중반에 그랬다.
1995	Schmidthuber는 언어를 위한 LSTM 뉴런을 도입합니다.
1995	Dayan & Hinton이 헬름홀츠 머신을 도입
1995-2005	(개산일) AI winter II
2013	Kingma, Rezende, and co.는 베이지안 그래픽 확률 네트워크로서 변형 자동 인코더를 도입하고, 뉴럴 넷을 컴포넌트로 했습니다.

특정 네트워크

여기에서는, 선택한 네트워크의 몇개의 특성을 강조합니다.각각에 대한 자세한 내용은 아래 비교표에 나와 있습니다.

Hopfield Network

강자성은 홉필드 네트워크에 영감을 주었습니다.뉴런은 2진수 자기 모멘트 Up과 Down을 가진 철 도메인에 대응하며, 신경 연결은 서로에 대한 도메인의 영향에 대응합니다.대칭 연결은 글로벌 에너지 공식을 가능하게 합니다.추론 중에 네트워크는 표준 활성화 단계 기능을 사용하여 각 상태를 업데이트합니다.대칭 가중치와 올바른 에너지 함수는 안정적인 활성화 패턴으로의 수렴을 보장합니다.비대칭 가중치는 분석하기가 어렵다.홉필드 네트워크는 Content Addressable Memory(CAM; 콘텐츠어드레스 가능 메모리)로서 사용됩니다.

Boltzmann Machine

이건 확률적 홉필드 그물이에요이들의 상태 값은 이 pdf에서 다음과 같이 샘플링된다. 이진 뉴런이 베르누이 확률 p(1) = 1/3로 작동하고 p(0) = 2/3로 유지된다고 가정한다.하나의 표본은 균일하게 분포된 난수 y를 취하여 반전 누적 분포 함수(이 경우 2/3에서 임계값화된 단계 함수)에 연결하여 추출합니다.역함수 = { x < = 2/3인 경우 0, x > 2/3인 경우 1}

Sigmoid Belief Net

1992년 Radford Neal에 의해 도입된 이 네트워크는 확률론적 그래픽 모델에서 신경 네트워크에 아이디어를 적용합니다.중요한 차이점은 그래픽 모델의 노드가 미리 할당된 의미를 가지는 반면, 믿음망 뉴런의 특징은 훈련 후에 결정된다는 것이다.네트워크는 이진 확률 뉴런으로 구성된 희박하게 연결된 지향성 비순환 그래프이다.학습규칙은 p(X)의 Maximum Life on p(X) : δw_ij $∝$ \$displaystyle \propto }$s$$_j * (s_i - p_i )에서 유래합니다.여기서_i p= 1 / ( 1 + e^{weighted inputs into neuron i})s는_j 후방 분포의 편향되지 않은 샘플로부터의 활성화이며, 이는 Judea Perl에 의해 제기된 "해방 설명" 문제로 인해 문제가 됩니다.변이형 베이지안 방법은 사후 대용품을 사용하며 이 복잡성을 노골적으로 무시한다.

Deep Belief Network

Hinton이 도입한 이 네트워크는 RBM과 Sigmoid Believe Network를 혼합한 것입니다.상위 2개의 레이어는 RBM이며, 2번째 레이어는 S자형 신뢰 네트워크를 형성합니다.적층 RBM 방식으로 훈련한 후 최상위 RBM 아래에 인식 가중치를 버립니다.2009년 시점에서는 3, 4층이 최적의 ^[3]깊이인 것 같습니다.

Helmholtz machine

Variational Auto Encoder에 대한 초기 영감입니다.2개의 네트워크가 하나로 결합되어 있습니다.전방 가중치는 인식을 실행하고 후방 가중치는 상상을 구현합니다.양쪽을 모두 실행하는 첫 번째 네트워크입니다.헬름홀츠는 기계학습에서 일하지 않았지만 "감각 입력의 가능한 원인을 추론하는 기능이 있는 통계적 추론 엔진"(3)의 관점을 고무시켰다. 확률적 이진 뉴런은 그 상태가 0 또는 1일 확률을 출력한다.데이터 입력은 일반적으로 계층으로 간주되지 않지만, Helmholtz 기계 생성 모드에서는 중간 계층으로부터 입력을 수신하는 데이터 계층이 이 목적을 위해 별도의 가중치를 가지므로 계층으로 간주됩니다.따라서 이 네트워크에는 3개의 레이어가 있습니다.

Variational autoencoder

이것들은 헬름홀츠 기계에서 영감을 받아 확률 네트워크와 신경 네트워크를 결합합니다.자동 인코더는 3층 CAM 네트워크입니다.중간층은 입력 패턴의 내부 표현입니다.인코더 신경망은 확률 분포_φ q(z 지정 x), 디코더 네트워크는 p(x 지정 z)입니다_θ.무게는 헬름홀츠에서처럼 W와 V가 아닌 phi와 Theta로 명명됩니다.이것은 외관상의 차이입니다.이 2개의 네트워크는 완전히 접속할 수도 있고 다른 NN 방식을 사용할 수도 있습니다.

네트워크 비교

	홉필드	볼츠만	RBM	스택형 RBM	헬름홀츠	자동 인코더	VAE
사용방법 및 주의사항	CAM, 출장 세일즈맨 문제	접속의 자유로움으로 인해 이 네트워크를 분석하기가 어렵습니다.	패턴 인식.MNIST 디짓과 음성으로 사용됩니다.	인식과 상상력. 감독되지 않은 사전 훈련 및/또는 감독된 미세 조정으로 훈련됩니다.	상상, 모방	언어: 창조적인 글쓰기, 번역.시각: 흐릿한 이미지 강화	현실적인 데이터를 생성하다
뉴런	결정론적 이진 상태활성화 = { 0(또는 -1) x가 음수이면 1(으)}	확률적 이항 홉필드 뉴런	← 동일(2000년대 중반의 실가치로 변경)	← 동일	← 동일	언어: LSTM 비전: 로컬 수용 필드.보통 실제 가치의 릴 활성화입니다.	중간층 뉴런은 가우시안들을 위한 평균과 분산을 부호화한다.실행 모드(추론)에서 중간 계층의 출력은 가우시안으로부터 샘플링된 값입니다.
접속	대칭 가중치를 가진 1-레이어.자기 연결 없음.	2중력, 1중력, 1중력, 1중력 대칭 가중치.	←동일. 레이어 내에 측면 연결부가 없습니다.	상단 레이어는 무방향 대칭입니다.다른 레이어는 2방향 비대칭 레이어입니다.	3단계: 비대칭 가중치2개의 네트워크가 1개로 결합됩니다.	스리볼트입력은 착신 웨이트가 없어도 레이어로 간주됩니다.NLP를 위한 반복 레이어. 시력을 위한 피드포워드 컨볼루션.입력과 출력의 뉴런 수는 동일합니다.	3 소켓: 입력, 인코더, 분배 썬플라 디코더샘플러는 레이어로 간주되지 않는다(e)
추론 및 에너지	$$는 깁스 확률 측도에 의해 주어진다: E ${\displaystyle =}$ - ${\displaystyle \frac{1}{}}$ 2${\displaystyle \underset{\mu }{}}$i , ${\displaystyle \underset{}{j}}$ ${\displaystyle w_{}}$ ${\displaystyle i_{}}$ ${\displaystyle s_{}}$ s ${\displaystyle s_{}}$j +${\displaystyle \underset{}{}{s}_{}}$ i ${\displaystyle {\theta }_{}}$ i θ i$$（ \ $displaystyle$ E = - { \ $frac {1$} ${2}$ } \ $sum$_ {$i$ } { w$_$ { $ij$} { s $_ { i }$} + \ $sum$ { $ta$}	← 동일	← 동일		KL의 차이를 최소한으로 억제하다	추론은 피드포워드일 뿐입니다.이전의 UL 네트워크는 전진과 후퇴를 반복했다.	오류 최소화 = 재구성 오류 - KLD
트레이닝	δW = sij*s, +1/-1 뉴런의 경우ij	θwij = e*(pij - ijp').이는 KLD를 최소화함으로써 도출된다. e = 학습률, p' = 예측 및 p = 실제 분포.	Wijii = e* ( < datavj h > - < equilibriumvj h > )이것은 Gibbs Sampling을 사용한 대조적 확산의 한 형태입니다."<>"는 기대 사항입니다.	← 유사합니다. 한 번에 1층을 교육합니다. 3-세그먼트 패스를 사용한 대략적인 평형 상태.후방 전파 없음.	웨이크 슬립 2단계 트레이닝	재구성 오류를 역전파하다	숨겨진 상태를 역추진용으로 재파라미터화하다
힘	물리 시스템과 유사하기 때문에 방정식을 계승합니다.	←같다. 숨겨진 뉴런은 외부 세계의 내적 표상 역할을 한다.	볼츠만 기계보다 더 빠른 실용적인 훈련 계획	빠르게 훈련합니다.기능의 계층 레이어를 제공합니다.	약간의 해부학적. 정보 이론과 통계 역학을 사용하여 분석할 수 있다.
약점		측면 연결로 인해 훈련하기 어렵다	평형은 너무 많은 반복을 필요로 한다	정수와 실제값의 뉴런은 더 복잡하다.

Hebbian Learning, ART, SOM
신경망의 연구에서 감독되지 않은 학습의 고전적인 예는 도날드 헵의 원리,^[4] 즉 함께 전선을 발사하는 뉴런이다.헤비어 학습에서, 연결은 오류에 관계없이 강화되지만, 두 ^[5]뉴런 사이의 활동 전위 사이의 일치의 함수만을 가지고 있다.시냅스 가중치를 변경하는 유사한 버전에서는 액션 전위(Spike-Timing-Dependent Plasticity(STDP; 스파이크타이밍 의존 플라스틱)) 사이의 시간이 고려됩니다.Hebbian Learning은 패턴 인식 및 경험적 학습과 같은 다양한 인지 기능의 기초가 되는 것으로 가정되어 왔다.

뉴럴 네트워크 모델 중, 자기 조직 지도(SOM)와 적응 공명 이론(ART)은 비지도 학습 알고리즘에 일반적으로 사용된다.SOM은 지도의 인근 위치가 유사한 속성을 가진 입력을 나타내는 지형 조직입니다.ART 모델은 클러스터의 수를 문제 크기에 따라 변경할 수 있도록 하며, 사용자는 경계 파라미터라고 불리는 사용자 정의 상수를 사용하여 동일한 클러스터의 구성원 간의 유사성 정도를 제어할 수 있도록 한다.ART 네트워크는 자동 표적 인식 및 지진 신호 ^[6]처리와 같은 많은 패턴 인식 작업에 사용됩니다.

확률론적 방법

비지도 학습에 사용되는 두 가지 주요 방법은 주성분과 클러스터 분석이다.클러스터 분석은 알고리즘 ^[7]관계를 추정하기 위해 공유 속성을 가진 데이터 세트를 그룹화하거나 세그먼트화하기 위해 비감독 학습에서 사용됩니다.클러스터 분석은 라벨, 분류 또는 분류되지 않은 데이터를 그룹화하는 기계 학습의 한 분야입니다.클러스터 분석은 피드백에 반응하는 대신 데이터의 공통점을 식별하고 새로운 데이터 조각마다 이러한 공통점의 유무에 따라 반응합니다.이 접근방식은 어느 그룹에도 적합하지 않은 비정상적인 데이터 포인트를 검출하는 데 도움이 됩니다.

비지도 학습은 데이터 특징을 요약하고 설명하는 많은 다른 영역을 포함하지만,^[8] 비지도 학습의 중심 적용 분야는 통계의 밀도 추정 분야이다.감독 학습은 입력 데이터의 라벨에 조건부 확률 분포를 추론하는 반면, 감독 학습은 선험적 확률 분포를 추론하는 것을 의도한다고 말함으로써 감독 학습과 대조될 수 있다.

접근

비지도 학습에 사용되는 가장 일반적인 알고리즘에는 (1) 클러스터링, (2) 이상 감지, (3) 잠재 변수 모델을 학습하기 위한 접근법이 포함된다.각 어프로치에서는, 다음과 같은 몇개의 방법은 다음과 같습니다.

• 클러스터링 방법에는 계층 클러스터링,^[9] k-평균,^[10] 혼합 모델, DBSCAN 및 Optics 알고리즘이 포함됩니다.
• 이상 검출 방법에는, 다음과 같은 것이 있습니다.로컬 특이치 계수 및 격리 포레스트
• 기대-최대화 알고리즘(EM), 모멘트 방법 및 블라인드 신호 분리 기법(주성분 분석, 독립성분 분석, 비음수 행렬 인수 분해, 특이값 분해)과 같은 잠재 변수 모델을 학습하기 위한 접근법

모멘트법

비지도 학습을 위한 통계적 접근법 중 하나는 순간의 방법이다.모멘트의 방법에서 모델 내의 미지의 파라미터(관심대상)는 하나 이상의 랜덤 변수의 모멘트와 관련되므로 모멘트가 주어졌을 때 이들 미지의 파라미터를 추정할 수 있다.모멘트는 보통 샘플로부터 경험적으로 추정됩니다.기본 모멘트는 1차 모멘트와 2차 모멘트가 있습니다.랜덤 벡터의 경우 1차 모멘트는 평균 벡터이고 2차 모멘트는 공분산 행렬(평균이 0인 경우)입니다.고차 모멘트는 보통 다차원 배열로서 행렬을 고차까지 일반화시킨 텐서를 사용하여 표현됩니다.

특히, 모멘트의 방법은 잠재 변수 모델의 매개변수를 학습하는 데 효과적인 것으로 나타났다.잠재 변수 모형은 관측된 변수 외에 관측되지 않은 일련의 잠재 변수도 존재하는 통계 모형이다.기계학습에서 잠재변수 모델의 매우 실용적인 예는 문서의 주제(잠재변수)에 기초하여 문서에서 단어(관측변수)를 생성하기 위한 통계 모델인 주제 모델링이다.토픽 모델링에서는 문서의 토픽이 변경되었을 때 다른 통계 파라미터에 따라 문서 내의 단어가 생성된다.모멘트 방법(텐서 분해 기법)은 일부 ^[11]가정 하에서 다수의 잠재 변수 모델의 매개변수를 일관되게 복구하는 것으로 나타났다.

기대-최대화 알고리즘(EM)은 잠재 변수 모델을 학습하기 위한 가장 실용적인 방법 중 하나이기도 합니다.단, 로컬 최적화에 걸릴 수 있으며 알고리즘이 모델의 진정한 미지의 파라미터로 수렴되는 것은 보증되지 않습니다.반면 모멘트의 방법에 대해서는 어떤 조건 하에서 글로벌컨버전스가 보증된다.

시리즈의 일부
기계 학습 및 데이터 마이닝
문제 분류 클러스터링 회귀 이상 검출 데이터 클리닝 자동 ML 어소시에이션 규칙 강화 학습 구조화된 예측 기능 엔지니어링 기능 학습 온라인 학습 준지도 학습 비지도 학습 순위 매기기 학습 문법 유도
지도 학습 (분류 • 회귀) 의사결정 트리 앙상블 배깅 부스팅 랜덤 포레스트 k-NN 선형 회귀 네이비 베이즈 인공신경망 로지스틱 회귀 분석 퍼셉트론 관련 벡터 머신(RVM) 서포트 벡터 머신(SVM)
클러스터링 버치 치유하다 계층적 k자형 기대 최대화(EM) DBSCAN 광학 평균 이동
치수 축소 인자 분석 CCA ICA LDA NMF PCA PGD t-SNE
구조화된 예측 그래픽 모델 베이즈 네트 조건부 랜덤 필드 히든 마르코프
이상 검출 k-NN 국소 특이치 계수
인공신경망 자동 인코더 인지 컴퓨팅 딥 러닝 딥 드림 다층 퍼셉트론 RNN LSTM GRU ESN 저장고 계산 제한 볼츠만 기계 GAN somerset. 컨볼루션 뉴럴 네트워크 유넷 트랜스포머 비전. 스파이킹 뉴럴 네트워크 메모리 트랜지스터 전기화학 RAM(ECRAM)
강화 학습 Q-러닝 사사 시간차(TD) 멀티 에이전트 셀프 플레이
인간과의 학습 액티브 러닝 크라우드 소싱 휴먼 인 더 루프
모델 진단 학습 곡선
이론. 커널 머신 바이어스-분산 트레이드오프 컴퓨터 학습 이론 경험적 리스크 최소화 오컴 러닝 PAC 학습 통계학 학습 VC 이론
기계학습장 NeurolIPS ICML ML JMLR ArXiv:cs.LG
관련 기사 인공지능 용어집 기계 학습 연구를 위한 데이터 세트 목록 기계학습의 개요
v t

「 」를 참조해 주세요.

• 자동 기계 학습
• 클러스터 분석
• 이상 검출
• 기대 최대화 알고리즘
• 생성 지형도
• 메타학습(컴퓨터과학)
• 다변량 분석
• 반지름 기준 함수 네트워크
• 감시가 약하다

레퍼런스

추가 정보

• Bousquet, O.; von Luxburg, U.; Raetsch, G., eds. (2004). Advanced Lectures on Machine Learning. Springer-Verlag. ISBN 978-3540231226.
• Duda, Richard O.; Hart, Peter E.; Stork, David G. (2001). "Unsupervised Learning and Clustering". Pattern classification (2nd ed.). Wiley. ISBN 0-471-05669-3.
• Hastie, Trevor; Tibshirani, Robert (2009). The Elements of Statistical Learning: Data mining, Inference, and Prediction. New York: Springer. pp. 485–586. doi:10.1007/978-0-387-84858-7_14. ISBN 978-0-387-84857-0.
• Hinton, Geoffrey; Sejnowski, Terrence J., eds. (1999). Unsupervised Learning: Foundations of Neural Computation. MIT Press. ISBN 0-262-58168-X.