홀수 그래프

Odd graph
홀수 그래프
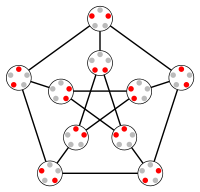Kneser graph KG(5,2).svg
O3 = KG는5,2 Petersen 그래프임
정점
가장자리
지름n − 1[1][2]
둘레if n = 2인 경우 3
n이 3이면 5
if n > 3이면[3]
특성.거리-변환
표기법On
그래프 및 모수 표
홀수 그래프4 O = KG7,3

그래프 이론의 수학적 영역에서 홀수 그래프 O는n 특정 세트 시스템에서 정의된 높은 홀수 둘레를 갖는 대칭 그래프 계열이다.그들은 피터슨 그래프를 포함하고 일반화한다.

정의 및 예제

홀수 그래프 O에는n (n - 1)-element subset a(2n - 1)-element set 각각에 대해 하나의 꼭지점이 있다.해당 서브셋이 분리된 경우에만 두 개의 정점이 에지로 연결된다.[2]즉, O는n Kneser 그래프 KG(2n - 1,n - 1)이다.

O는2 삼각형이고 O는3 친숙한 피터슨 그래프다.

일반화 홀수 그래프는 일부 n의 경우 지름 n - 1과 홀수 둘레 2n - 1의 거리 정규 그래프로 정의된다.[4]여기에는 홀수 그래프와 접힌 입방체 그래프가 포함된다.

기록 및 응용 프로그램

피터슨 그래프는 1898년부터 알려져 있지만, 홀수 그래프로서의 정의는 홀수 그래프 O를4 연구하기도 한 코왈레프스키(1917년)의 저작에 기인한다.[2][5]화학 그래프 이론에서, 카르보늄 이온의 변화를 모델링하는 데 있어서, 홀수 그래프는 그 적용에 대해 연구되어 왔다.[6][7]그것들은 또한 병렬 컴퓨팅에서 네트워크 토폴로지로 제안되었다.[8]

이 그래프들의 표기법n O는 1972년 노먼 빅스에 의해 도입되었다.[9]빅스와 토니 가디너는 1974년부터 출판되지 않은 원고에서 홀수 그래프의 이름을 설명하고 있다: 홀수 그래프의 각 가장자리에는 "이상한 인간 아웃"인 X의 고유한 요소가 할당될 수 있다. 즉, 그 가장자리까지 정점 사건과 관련된 부분 집합의 멤버가 아니다.[10][11]

특성.

홀수 그래프 O는n 도 n의 정규 그래프 입니다.- - ) 정점과 n(- - 1)/ 의 가장자리가 있다.따라서 n = 1, 2, ...의 정점 수이다

1, 3, 10, 35, 126, 462, 1716, 6435(OEIS에서 시퀀스 A001700).

거리와 대칭

O의n 두 꼭지점이 한 세트에서 k 요소를 제거하고 k개의 다른 요소를 추가함으로써 서로 다른 세트에 해당하는 경우, 각각 하나의 추가와 제거를 수행하는 2k 단계로 서로 도달할 수 있다.2k < n, 이것이 최단 경로인 경우, 그렇지 않으면 첫 번째 세트에서 두 번째 세트와 보완되는 세트로 이 유형의 경로를 찾은 후 한 단계 더 나아가 두 번째 세트에 도달하는 것이 더 짧다.따라서 O의n 지름은 n - 1이다.[1][2]

모든 홀수 그래프는 3arc-transitive이다. 홀수 그래프에 있는 모든 방향 3 에지 경로는 그래프의 대칭에 의해 다른 모든 경로로 변환될 수 있다.[12]홀수 그래프는 거리 전이성이므로 거리가 정규적이다.[2]거리 정규 그래프는 교차로 배열에 의해 고유하게 정의된다. 다른 거리 정규 그래프는 홀수 그래프와 동일한 파라미터를 가질 수 없다.[13]그러나, 높은 대칭도에도 불구하고, n > 2에 대한 홀수 그래프n O는 결코 Cayley 그래프가 아니다.[14]

홀수 그래프는 정규적이고 에지 변환적이기 때문에 정점 연결은 그 정도, n과 같다.[15]

n > 3의 홀수 그래프에는 6번째 그래프가 있지만, 두 번째 그래프는 아니지만 홀수 주기는 훨씬 더 길다.특히 홀수 그래프 O는n 홀수 둘레 2n - 1을 가지며, n-정규 그래프의 직경이 n - 1과 홀수 둘레 2n - 1이며, 고유값이 n 구별되지 않는 경우에는 거리 정규 그래프여야 한다.지름 n - 1과 홀수 둘레 2n - 1의 거리 정규 그래프를 일반화된 홀수 그래프라고 하며, 접힌 입방체 그래프뿐만 아니라 홀수 그래프도 포함한다.[4]

독립 세트 및 정점 색상

O를n a(2n - 1)-element set X의 하위 집합에서 정의한 홀수 그래프로 하고 x를 X의 임의의 멤버로 한다.그러면 O의n 정점 중에서 정확히(- - ) n-2의 정점은 x를 포함하는 세트에 해당된다. 이 모든 세트가 x를 포함하기 때문에 분리되지 않으며, O의n 독립된 집합을 형성한다.에서}크기(2n− 2n− 2){\displaystyle{\tbinom{2n-2}{n-2}의 2n − 1 다른 독립적인 세트가 있으면}. 그것은 Erdős–Ko–Rado 정리에서 온의 이것들이 최대 독립 집합을 따른다. 그것은 On의 독립 수.{\displaystyle{\tbinom{2n-2}{n-2(2n− 2n− 2) 것입니다.}} 또한 모든 최대 독립 집합에는 이 형식이 있어야 하므로 O는n 정확히 2n - 1의 최대 독립 집합을 가지고 있다.[2]

만약 내가 x를 포함하는 집합에 의해 형성된 최대 독립 집합이라면, I의 보완점은 x를 포함하지 않는 정점 집합이다.이 보완적 집합은 G에서 일치를 유도한다. 독립 집합의 각 정점은 일치의 n 정점에 인접하고, 일치의 각 정점은 독립 집합의 n - 1 정점에 인접한다.[2]이러한 분해로 인해, 그리고 홀수 그래프는 초당적인 것이 아니기 때문에 세 번째 색상을 가지고 있다: 최대 독립 집합의 정점에는 하나의 색상을 할당할 수 있고, 두 가지 색상은 보완적 일치를 색칠하기에 충분하다.

엣지 컬러링

바이징의 정리로는 홀수 그래프 O의n 가장자리를 색칠하는 데 필요한 색의 수가 n 또는 n + 1이고, 피터슨 그래프 O의3 경우 n + 1이다.n이 2의 검정력일 때 그래프에서 정점의 수는 홀수인데, 여기서부터 다시 에지 색의 수가 n + 1이라는 것을 따라간다.[16]그러나 O5, O6, O는7 각각 n가지 색으로 엣지 색상이 될 수 있다.[2][16]

Biggs[9] explains this problem with the following story: eleven soccer players in the fictional town of Croam wish to form up pairs of five-man teams (with an odd man out to serve as referee) in all 1386 possible ways, and they wish to schedule the games between each pair in such a way that the six games for each team are played on six different days 매주 일요일은 모든 팀이 쉬는 날이야.그렇게 할 수 있을까?이 이야기에서 각 게임은 O의6 엣지를 나타내고, 평일은 컬러로 표현되며, O의6 6가지 색상의 엣지 컬러링은 선수들의 스케줄링 문제를 해결해 준다.

해밀턴시티

피터슨 그래프 O는3 해밀턴식 그래프로 잘 알려져 있지만, n ≥ 4의 모든 홀수 그래프 O는n 해밀턴식 사이클을 갖는 것으로 알려져 있다.[17]홀수 그래프는 정점 변환이므로, 로바스의 추측에 대한 긍정적인 답변이 알려진 특별한 경우 중 하나이다.Biggs는[2] 보다 일반적으로n O의 가장자리를 / n 엣지 분리 해밀턴 사이클로 분할할 수 있다고 추측했다.n이 이상할 경우, 남은 가장자리가 완벽하게 일치해야 한다.이 더 강한 추측은 n = 4, 5, 6, 7에 대해 검증되었다.[2][16] n = 8의 경우, O의n 홀수 정점 수는 8색 가장자리 색상이 존재하는 것을 방지하지만, 4개의 해밀턴 사이클로 분할될 가능성을 배제하지 않는다.

참조

  1. ^ a b Biggs, Norman L. (1976), "Automorphic graphs and the Krein condition", Geometriae Dedicata, 5 (1): 117–127, doi:10.1007/BF00148146.
  2. ^ a b c d e f g h i j Biggs, Norman (1979), "Some odd graph theory", Second International Conference on Combinatorial Mathematics, Annals of the New York Academy of Sciences, 319: 71–81, doi:10.1111/j.1749-6632.1979.tb32775.x.
  3. ^ West, Douglas B. (2000), "Exercise 1.1.28", Introduction to Graph Theory (2nd ed.), Englewood Cliffs, NJ: Prentice-Hall, p. 17.
  4. ^ a b Van Dam, Edwin; Haemers, Willem H. (2010), An Odd Characterization of the Generalized Odd Graphs, CentER Discussion Paper Series No. 2010-47, SSRN 1596575.
  5. ^ Kowalewski, A. (1917), "W. R. Hamilton's Dodekaederaufgabe als Buntordnungproblem", Sitzungsber. Akad. Wiss. Wien (Abt. IIa), 126: 67–90, 963–1007. Biggs(1979년)가 인용한 바와 같다.
  6. ^ Balaban, Alexandru T.; Fǎrcaşiu, D.; Bǎnicǎ, R. (1966), "Graphs of multiple 1, 2-shifts in carbonium ions and related systems", Rev. Roum. Chim., 11: 1205.
  7. ^ Balaban, Alexandru T. (1972), "Chemical graphs, Part XIII: Combinatorial patterns", Rev. Roumaine Math. Pures Appl., 17: 3–16.
  8. ^ Ghafoor, Arif; Bashkow, Theodore R. (1991), "A study of odd graphs as fault-tolerant interconnection networks", IEEE Transactions on Computers, 40 (2): 225–232, doi:10.1109/12.73594.
  9. ^ a b Biggs, Norman (1972), Guy, Richard K. (ed.), "An edge-colouring problem", Research Problems, American Mathematical Monthly, 79 (9): 1018–1020, doi:10.2307/2318076, JSTOR 2318076.
  10. ^ Brouwer, Andries; Cohen, Arjeh M.; Neumaier, A. (1989), Distance-regular Graphs, ISBN 0-387-50619-5.
  11. ^ Ed Pegg, Jr. (December 29, 2003), Cubic Symmetric Graphs, Math Games, Mathematical Association of America, archived from the original on August 21, 2010, retrieved August 24, 2010.
  12. ^ Babai, László (1995), "Automorphism groups, isomorphism, reconstruction", in Graham, Ronald L.; Grötschel, Martin; Lovász, László (eds.), Handbook of Combinatorics, vol. I, North-Holland, pp. 1447–1540, Proposition 1.9, archived from the original on June 11, 2010.
  13. ^ Moon, Aeryung (1982), "Characterization of the odd graphs Ok by parameters", Discrete Mathematics, 42 (1): 91–97, doi:10.1016/0012-365X(82)90057-7.
  14. ^ Godsil, C. D. (1980), "More odd graph theory", Discrete Mathematics, 32 (2): 205–207, doi:10.1016/0012-365X(80)90055-2.
  15. ^ Watkins, Mark E. (1970), "Connectivity of transitive graphs", Journal of Combinatorial Theory, 8: 23–29, doi:10.1016/S0021-9800(70)80005-9, MR 0266804
  16. ^ a b c Meredith, Guy H. J.; Lloyd, E. Keith (1973), "The footballers of Croam", Journal of Combinatorial Theory, Series B, 15 (2): 161–166, doi:10.1016/0095-8956(73)90016-6.
  17. ^ Mütze, Torsten; Nummenpalo, Jerri; Walczak, Bartosz (2018), "Sparse Kneser graphs are Hamiltonian", STOC'18—Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing, New York: ACM, pp. 912–919, arXiv:1711.01636, MR 3826304

외부 링크