3차원 입체 대칭

3차원의 점 그룹

비자발적 대칭 Cs, (*) [ ] =	순환 대칭 Cnv, (*n) [n] =	치측 대칭 Dnh, (*n22) [n,2] =
다면군, [n,3], (*n32)
사면 대칭 Td, (*332) [3,3] =	팔면 대칭 Oh, (*432) [4,3] =	이코사면 대칭 Ih, (*532) [5,3] =

기하학에서 3차원의 치골 대칭은 3차원의 점군들의 3개의 무한 순서 중 하나이며, 대칭 그룹은 추상적인 집단으로서 치골군 Dih_n (n ≥ 2의 경우)이다.

종류들

3차원의 치대칭에는 3가지 유형이 있으며, 각각 다음과 같은 3가지 개념으로 표시된다.쇤파리 표기법, 콕시터 표기법, 오비폴드 표기법.

치랄

• D_n, [n,2],⁺ (22n) 순서 2n – 이음 대칭 또는 파라 n-곤갈 그룹(추상 그룹: Dih_n)

아키랄

• D_nh, [n,2], (*22n) 순서 4n – 프리즘 대칭 또는 전체 직교-n-곤갈 그룹(추상 그룹:Dih_n × Z₂).
• 4n_nd 순서의_nv D(또는 D), [2n⁺,2], (2*n) – 반격 대칭 또는 완전한 자이로-고날 그룹(추상 그룹: Dih_2n)

주어진 n의 경우, 세 개 모두 한 축에 대한 n-폴드 회전 대칭( 360°/n 각도로 회전해도 물체는 변하지 않음)과 수직 축에 대한 2-폴드 회전 대칭(따라서 n개)을 가지고 있다.n = ∞의 경우, 그들은 3개의 프리제 그룹에 해당한다.괄호에는 콕시터 표기법을, 괄호에는 오비폴드 표기법을 사용한다.수평(h)이라는 용어는 수직 회전 축과 관련하여 사용된다.

2D에서 대칭군 D는_n 선에 반사를 포함한다.2D 평면이 3D 공간에 수평으로 내장되는 경우, 그러한 반사는 수직 평면을 통한 반사 면에 대한 제한 또는 반사선에 대한 회전 면에 대한 제한 180°로 볼 수 있다.3D에서는 D그룹이_n 반사가 아닌 회전만을 포함하고 있다는 두 가지 연산을 구별한다.다른 그룹은 같은 순서인 2n의 피라미드_nv 대칭 C이다.

N-폴드 회전 축에 수직인 평면의 반사 대칭으로 D_nh, [n], (*22n)을 갖는다.

D_nd(또는 D_nv), [2n,2⁺], (2*n)는 수평 회전 축 사이를 통과하지 않고 수직 미러 평면을 가진다.그 결과 수직축은 2n배 회전선택축이다.

D는_nh 정규 n면 프리즘과 정규 n면 bipyramid의 대칭군이다.D는_nd 정규적인 n측 항정신병, 또한 정규 n측 사다리꼴의 대칭군이다.D는_n 부분 회전 프리즘의 대칭군이다.

n = 1은 세 대칭이 다른 대칭과 같기 때문에 포함되지 않는다.

• D와₁ C₂: 180° 회전 한 번으로 순서 2의 그룹.
• D와_1h C_2v: 평면에 반사되고 해당 평면의 선에 대해 180° 회전하는 순서 4의 그룹.
• D와_1d C_2h: 평면에 반사되고 해당 평면에 수직인 선에 대해 180° 회전하는 순서 4의 그룹.

n = 2의 경우 주축이 1개, 추가축이 2개가 아니라 등가축이 3개 있다.

• 순서₂ 4의 D, [2,2],⁺ (222)는 클라인 4그룹을 추상그룹으로 하는 세 가지 대칭군 유형 중 하나이다.3개의 수직 2배 회전축을 가지고 있다.그것은 같은 방향으로 반대편 두 면에 S가 쓰여진 큐보이드의 대칭 그룹이다.
• D_2h, 순서 8의 [2,2], (*222)는 입체파의 대칭군이다.
• D_2d, 순서 8의 [4,2⁺](2*2)는 다음과 같은 대칭군이다.
  • 한 사각 면에 대각선을 그리고 다른 면에 수직 대각선을 그리는 사각형 입체형이다.
  • 두 개의 반대쪽 가장자리의 중간점을 연결하는 선의 방향으로 스케일링되는 정규 사면체(D는_2d T의_d 부분군이며, 스케일링을 통해 대칭을 감소시킨다).

부분군

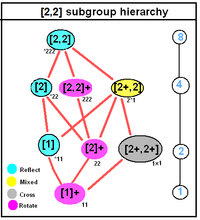D2h, [2,2], (*222)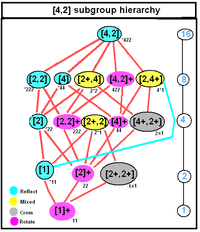

D4h, [4,2], (*224)

D_nh, [n,2], (*22n)의 경우 4n을 주문

• C_nh, [n⁺,2], (n*), 주문 2n
• C_nv, [n,1], (*nn), 주문 2n
• D_n, [n,2],⁺ (22n), 주문 2n

D_nd, [2n,2⁺], (2*n)의 경우 4n을 주문한다.

• S_2n, [2n⁺,2⁺], (n×), 주문 2n
• C_nv, [n⁺,2], (n*), 주문 2n
• D_n, [n,2],⁺ (22n), 주문 2n

D는_nd 또한_2nh D의 부분군이다.

예

D2h, [2,2], (*222) 주문 8	D2d, [4,2+], (2*2) 주문 8	D3h, [3,2], (*223) 순서 12
농구심길	야구심로 (심의 방향성 감소)	비치볼 (색상 색상 변경)

D_nh, [n], (*22n):

프리즘

D_5h, [5], (*225):

펜타그램 프리즘

펜타그램 항정신병

D_4d, [8,2⁺], (2*4):

스너브 사각 항정신병

D_5d, [10,2⁺], (2*5):

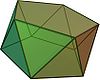오각 항정신병

펜타그램 교차 안티프리즘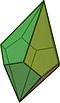

오각형 사다리꼴

D_17d, [34,2⁺], (2*17):

헵타데크각형 항정신병

참고 항목

• 구면 대칭군 목록
• 3차원의 점 그룹
• 3차원의 주기적 대칭

참조

• Coxeter, H. S. M. and Moser, W. O. J. (1980). Generators and Relations for Discrete Groups. New York: Springer-Verlag. ISBN 0-387-09212-9.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)
• N.W. 존슨: 기하학과 변환, (2018) ISBN 978-1-107-10340-5장 11: 유한대칭군, 11.5 구형 콕시터군
• Conway, John Horton; Huson, Daniel H. (2002), "The Orbifold Notation for Two-Dimensional Groups", Structural Chemistry, Springer Netherlands, 13 (3): 247–257, doi:10.1023/A:1015851621002

외부 링크

• 32개의 결정학적 점 그룹의 그래픽 개요 – 7개의 무한 시리즈 중 첫 번째 부분(n=5)과 7개의 개별 3D 점 그룹 중 5개를 건너뛰지 않음