푸시-릴라벨 최대 흐름 알고리즘

수학적 최적화에서 푸시-릴라벨 알고리즘(대안적으로, 프리플로우-푸시 알고리즘)은 흐름 네트워크의 최대 흐름을 계산하기 위한 알고리즘이다."push-relabel"이라는 이름은 알고리즘에서 사용되는 두 가지 기본 연산으로부터 유래한다.실행 내내 알고리즘은 "사전 흐름"을 유지하며, 리라벨 연산에 의해 유지되는 허용 가능한 네트워크의 지침에 따라 푸시 연산을 이용하여 이웃 노드들 사이에서 로컬로 흐름을 이동하여 점진적으로 최대 흐름으로 변환한다.이에 비해 포드-풀커슨 알고리즘은 소스에서 싱크대까지 이어지는 경로를 전송하는 전지구적 확장을 수행한다.^[1]

푸시-릴라벨 알고리즘은 가장 효율적인 최대 흐름 알고리즘 중 하나로 간주된다.일반 알고리즘은 강력한 다항식 $O (VE 2)$ 시간 복잡성을 가지고 있는데, 이는 점증적으로 $O (VE 2$ ) Edmonds-Karp 알고리즘보다 효율적이다.^[2]알고리즘의 특정 변형은 훨씬 더 낮은 시간 복잡성을 달성한다.가장 높은 라벨 노드 선택 규칙에 기초한 변종은 $O (V 2 (E)$ 시간 복잡성을 가지며 일반적으로 최대 흐름 알고리즘의 벤치마크로 간주된다.^[3]^[4]아큐빅 $O (VELOG(V 2 / E)$ 시간 복잡성은 동적 트리를 사용하여 달성할 수 있지만 실제로는 덜 효율적이다.^[2]

푸시-릴라벨 알고리즘이 최소 비용 흐름을 계산하도록 확장되었다.^[5]거리 라벨의 아이디어는 보다 효율적인 증강 경로 알고리즘으로 이어졌고, 이는 다시 푸시-릴라벨 알고리즘에 통합되어 훨씬 더 높은 경험적 성능을 가진 변형을 만들 수 있다.^[4]^[6]

역사

프리플로우의 개념은 원래 알렉산더 V. 카르자노프에 의해 고안되었으며 1974년 소비에트 수학 도클라디 15에 발표되었다.이 프리 플로우 알고리즘은 푸시 연산도 사용했지만, 라벨링 시스템 대신 플로우를 어디에 밀어넣어야 할지를 결정하기 위해 보조 네트워크의 거리를 사용했다.^[2]^[7]

푸시-릴라벨 알고리즘은 앤드류 V. 골드버그와 로버트 타르잔에 의해 설계되었다.이 알고리즘은 처음에는 1986년 11월에 STOC '86: 연산 이론에 관한 제18차 연례 ACM 심포지엄의 진행에서 발표되었다가 1988년 10월에 ACM 저널의 기사로 공식 발표되었다.두 논문 모두 $O (V 3)$ 순차 구현, 동적 트리를 이용한 $O (VE$ $로그(V 2 / E)$ 구현, 병렬/분산 구현과 함께 $O (VE 2)$ 로 종료되는 알고리즘의 일반적인 형태를 상세히 기술하고 있다.^[2]^[8]골드버그-타르잔에서 설명한 A는 거리 라벨을 요시 쉴로치와 우지 비슈킨의 평행 최대 흐름 알고리즘에 통합해 도입했다.^[10]

개념

정의 및 표기

허용:

G $=$ ( $V$ $,$ E $)$ 용량 함수 $c :$ V × $\mathbb {R}$ → R ${\$
$F =$ ( $G,$ $c,$ $s,$ $t)$ 흐름 네트워크, 여기에서 $s$ ∈ $V$ 와 $t$ ∈ $V$ 는 각각 소스와 싱크 정점을 선택한다.
$f$ : $\mathbb {R}$ × $V$ → R ${\$ 은 $\mathbb {R}$ (는) $F$ 의 사전 흐름을 나타낸다.
$\mathbb {R}$ : $V$ → $\mathbb {R}$ ${\$ 는) $x f$ ( $u)$ = = $f v \in V$ ( $v,$ $u)$ - $σ v \in V$ $f$ ( $u,$ $v),$
$c f$ : $V$ × $V$ → $\mathbb {R}$ ${\$ 은(는) $c f$ ( $e)$ = $c (e)$ - $f$ ( $e)$ 로 정의되는 $f$ 에 대한 잔류 용량 함수를 나타낸다 $\mathbb {R}$ .
$E f$ ⊂ $E$ 는 f < $c$ 가 있는 가장자리,

그리고

$G f$ ( $V,$ $E f)$ 는 흐름 $f$ 에 관한 $G$ 의 잔류 네트워크를 나타낸다.

푸시-릴라벨 알고리즘은 푸시 작동을 위해 선택해야 하는 호를 결정하기 위해 노드의 거리 라벨 또는 높이를 사용하는 음이 아닌 정수 유효 라벨링 기능을 사용한다.이 라벨링 함수는 $𝓁$ : $\mathbb {N}$ → N ${\$ 로 표시된다 $\mathbb {N}$ 이 함수는 유효하다고 간주되려면 다음 조건을 충족해야 한다.

유효한 라벨링:

𝓁(u) \leq(v)

+

전체 f

(

u,

v)

∈ E

소스 조건:

𝓁 = V

싱크 보존:

𝓁(t) = 0

알고리즘에서 $s$ 와 $t$ 의 라벨 값은 고정되어 있다. $𝓁(u)$ 는 $t$ 가 $u$ 에서 도달할 수 있는 경우 $G$ 에서_f $u$ 에서 $t$ 까지의 비가중 거리의 하한이다. $u$ 와 $t$ 의 연결이 끊어진 경우, $𝓁(u)$ - $V$ 는 $u$ 에서 $s$ 까지의 비가중 거리의 하한이다.그 결과 유효한 라벨링 함수가 존재하는 경우, 그러한 경로가 $V$ - $1$ 보다 길 수 없기 때문에 $G$ 에는_f $s-t$ 경로가 없다.

𝓁 $(u,$ v)∈ $E$ 는_f $𝓁(u)$ = $𝓁(v)$ + $1$ 이면 admit conceptable이라고 한다. 인정 가능한 네트워크 $G ̃(f V,$ $ẽ f$ )은 인정 가능한 arc $e$ ∈ $E$ 의_f 집합으로 구성된다.허용 가능한 네트워크는 반복적이다.

고정 흐름 $f$ 의 경우, $f$ , 즉 $x f$ ( $u)$ > $0$ 에 대해 양의 초과가 있으면 꼭지점 $v$ 를 활성이라고 한다.

운영

초기화

알고리즘은 잔차 그래프를 생성하여 프리플로 값을 0으로 초기화하고 소스에서 나가는 잔여 호 $(s,$ $v)$ 에 대해 포화 푸시 연산을 수행하는 것으로 시작한다. $여기$ 서 $v$ ∈ $V$ $\$ { $s}.$ 마찬가지로 소스의 라벨이 그래프에 있는 노드 수, is( $s)$ = $V$ , 그리고 다른 모든 노드에 0의 라벨이 주어지도록 라벨을 초기화한다.초기화가 완료되면 알고리즘은 해당 연산이 수행되지 않을 때까지 활성 노드에 대해 푸시 또는 리라벨 연산을 반복적으로 수행한다.

밀다

푸시 연산은 $G$ 에서_f 활성 노드 $u$ 의 허용 가능한 아웃아크 $(u,$ $v)$ 에 적용된다. $최소{x f (u),$ $c f (u, v)}$ 단위의 흐름을 $u$ 에서 $v$ 로 이동시킨다.

push(u, v):     assert x_f[u] > 0 and 𝓁[u] == 𝓁[v] + 1     Δ = min(x_f[u], c[u][v] - f[u][v])     f[u][v] += Δ     f[v][u] -= Δ     x_f[u] -= Δ     x_f[v] += Δ

$f (u,$ $v)$ 가 $c (u,$ $v)$ 에 도달하게 하는 푸시 연산을 잔류 아크의 가용 용량을 모두 소모하기 때문에 포화 푸시라고 한다.그렇지 않으면 노드의 모든 초과가 잔류 호를 가로질러 밀린다.이것을 불포화 또는 불포화 푸시라고 한다.

렐라벨

Relabel 작동은 $G$ 에서_f 허용 가능한 외부 호가 없는 활성 노드 $u$ 에 적용된다. $허용$ 가능한 아웃아크가 생성되도록 최소값으로 created( $u)$ 을 수정한다.이는 항상 $𝓁(u)$ 를 증가시키고 절대 가파른 호를 생성하지 않는다는 점에 유의하십시오. $이 f$ 호는 c $(u,$ $v)$ > $0$ , $𝓁(v$ ) + $1$ 과 같은 $호$ ( $u$ , v)이다.

elabel(u): c_f[u][v] > 0과 0과 같은 모든 v에 대해 x_f[u] > 0과 𝓁[v]를 주장하십시오. c_f[u] = 1 + min[v], c[u] > 0)

푸시 및 리라벨 효과

푸시 또는 리라벨 작동 후, $𝓁$ 은 $f$ 에 대해 유효한 라벨링 함수를 유지한다.

허용 가능한 호 $(u,$ $v$ )에 대한 푸시 연산의 경우, $𝓁(v)$ = $𝓁(u)$ - $1$ ≤( $u)$ + $1$ 에 호 $(u$ )를 $추가$ 할_f 수 있으며, $𝓁(u$ ) $\leq(v)$ + $1$ 을 효과적으로 제거하는 $E$ 에서도_f 호 $(u,$ $v)$ 를 제거할 수 있다.

노드 $u$ 에 대한 리라벨 작업이 $𝓁(u$ )의 유효성을 보존하는 것을 확인하기 위해, $이$ 는_f G에서 u의 아웃아크에 대해 정의에 의해 사소한 것으로 보증된다는 점에 주목한다 $.$ $G$ 에서_f $u$ 의 arcs의 경우, 증가된 $((u)$ 는 제약조건을 위반하지 않고 덜 단단하게 충족시킬 수 있을 뿐이다.

일반 푸시-릴라벨 알고리즘

일반 푸시-릴라벨 알고리즘은 개념 증명으로만 사용되며 푸시 및 리라벨 작동을 위해 활성 노드를 선택하는 방법에 대한 구현 상세 내역은 포함하지 않는다.이 알고리즘의 일반 버전은 $O (VE 2$ )로 종료된다 $.$

$𝓁(s)$ = $V$ , $𝓁(t)$ = $0$ 이고, $G$ 에_fV - $1$ 보다 긴 경로가 없기 때문에, $𝓁(s)$ 가 유효한 라벨링 $조건$ 을 만족시키려면 $t$ 에서 분리해야 한다.초기화할 때 알고리즘은 $s$ 의 모든 외부 호를 포화시키는 사전 흐름 $f$ 를 생성하여 이 요구 사항을 충족하며, 그 후 $((v)$ = $0$ 은 $모든$ $V \$ { $s, t$ }에 대해 소상하게 유효하다.초기화 후 알고리즘은 그러한 연산이 적용되지 않을 때까지 적용 가능한 푸시 또는 리라벨 연산을 반복적으로 실행하며, 이때 사전 흐름이 최대 흐름으로 변환된다.

일반 푸시-릴라벨(G, c, s, t): 해당하는 푸시 또는 릴라벨 작업이 작업을 실행하는 동안 s let let[s] = V lett [v] = 0으로 모든 v \ V \ {s}에 대해 s의 모든 범위를 포화시키는 사전 흐름 f 생성

정확성

알고리즘은 실행 중에 $𝓁$ 이 유효한 라벨이라는 조건을 유지한다.이는 푸시 및 리라벨 연산이 라벨 함수 $𝓁$ 에 미치는 영향을 조사함으로써 사실임을 증명할 수 있다.라벨 연산은 $minimum$ ( $u) \leq(v)$ + $1$ 구속조건을 항상 만족시키는 관련 최소 + 라벨 값을 증가시킨다.만약 𝓁(u))𝓁(v)+1은 추진 운전. 이 Gf고 Gf에서. 이후 𝓁(v))𝓁(u)𝓁(u)≤ 𝓁(v)1+만 보강에 적용된다 − 1.Gf에서(u, v)의 그 삭제 자체가 유효한 라벨링 속성부터 해당 제약 조건 제거합니다(v마)의 Gf 추가는 유효한 라벨링에 영향을 미치지 않을 것이다(u, v)삭제할 수 있고(v마)을 추가할 것인지 u에서 v 보낼 수 있다.sidual arcs in $G f$ .^[8]

만약 preflow $f$ 와 $f$ 에 대한 유효한 $라벨링$ 이 존재한다면, 잔차 그래프 $G$ 에는_f $s$ 에서 $t$ 까지의 증강 경로가 존재하지 않는다. 이는 증가 경로가 존재한다고 가정할 때 라벨링 함수에 발생하는 불평등에 근거한 모순에 의해 증명될 수 있다.알고리즘이 종료되면 $V$ $\$ { $s,$ $t}$ 의 모든 노드가 활성화되지 않는다.즉, 모든 $v$ ∈ $V$ $\$ { $s,$ $t}$ 은(는) 초과 유량이 없으며, 초과 유량이 없으면 $전유량$ f는 유량 보존 제약조건을 준수하며 정상적인 유량으로 간주될 수 있다.이 흐름은 $s$ 에서 $t$ 까지의 증강 경로가 없기 때문에 최대 흐름 최소 절단 정리에 따른 최대 흐름이다.^[8]

따라서 알고리즘은 종료 시 최대 흐름을 반환한다.

시간 복잡성

알고리즘의 시간 복잡성을 바인딩하기 위해서는 메인 루프 내에서 발생하는 푸시 및 리라벨 작동 횟수를 분석해야 한다.리라벨, 포화 푸시 및 불포화 푸시 작동의 수는 별도로 분석한다.

알고리즘에서는 최대 $(2$ V - 1) $(V$ - 2 $)$ > 2 $V$ 회에서 라벨 작동을 수행할 수 있다.이는 어떤 노드 u에 대해서도 라벨링 labeling $(u)$ 값은 절대 감소할 수 없으며, 최대 라벨 값은 모든 노드에 대해 최대 $2$ $V$ - $1$ 이기 때문이다.즉, 모든 노드 $V$ $\$ { $s,$ $t}($ 예: V - 2)에 대해 $2V$ - $1회$ 다시 라벨 작업을 수행할 수 있다는 의미.이로 인해 Relabel 작동에 O( $V 2)$ 가 바운드된다.

허용 가능한 호 $(u,$ $v)$ 에 대한 각 포화 푸시는 $G$ 에서_f 호를 제거한다. 호를 다시 포화 푸시하기 위해 $G$ 에_f 다시 삽입하려면 $먼저$ v를 다시 부착한 후 호 $(v,$ $u$ )를 $눌러야$ 한다 $.$ 이 과정에서 $𝓁(u)$ 는 최소 2씩 증가한다.따라서 $O (V)$ 포화 푸시 $(u,$ $v$ )가 있으며 $,$ 포화 푸시 총 횟수는 최대 2 $V$ $E$ . 포화 푸시 작업에 대한 $O (VE)$ 의 시간 바인딩이 된다.

불포화 푸시 횟수를 경계하는 것은 잠재적 논쟁을 통해 달성될 수 있다.잠재적 함수 $φ$ = $σ [u \in V \land x f (u) > 0] 𝓁(u)$ 를 사용한다(즉, $φ$ 은 모든 활성 노드의 라벨의 합이다). $φ$ 은 초기에는 $0$ 이고 알고리즘의 실행 내내 음성이 아닌 상태로 유지된다는 것은 명백하다.리라벨과 포화 푸시는 모두 $both$ 을 증가시킬 수 있다.단, 알고리즘 실행 종료 시 나머지 $활성$ 노드가 있을 수 없으므로 at 값은 종료 시 0과 같아야 한다.즉, 알고리즘의 실행에서 불포화 푸시는 $Ⅱ가$ 0의 값으로 종료되기 위해서는 리라벨과 포화 푸시 연산의 차이를 보충해야 한다.라벨 작동은 최대 $(2$ $V$ - 1) $(V$ - 2)만큼 $by$ 을 증가시킬 수 있다 $.$ 포화 푸시 $($ $u$ $,$ v $)$ 는 푸시 전에 비활성화된 경우 $v$ 를 활성화하여 $최대$ 2 $V$ - 1 $φ만큼$ φ을 증가시킨다. 따라서 pushes에 대한 모든 포화 푸시 작업의 총 기여도는 최대 ( $2$ V - $1)(2 V$ $E).$ 불포화 푸시 ( $u$ $,$ $v)$ 는 항상 u를 비활성화하지만 포화 푸시처럼 $활성화$ 할 수도 있다.As a result, it decreases $Φ$ by at least $𝓁(u) - 𝓁(v) = 1$ . Since relabels and saturating pushes increase $Φ$ , the total number of nonsaturating pushes must make up the difference of $(2 V - 1)(V - 2) + (2 V - 1)(2 V E) \leq 4 V 2 E$ . This results in a time bound of $O (V 2 E)$ for the nonsaturating push operations.

요약하면 알고리즘은 $O (V 2)$ 리라벨, $O (VE)$ 포화 푸시 및 $O (VE 2)$ 불포화 푸시를 실행한다.데이터 구조는 $해당$ 작업을 O $(1)$ 시간 내에 선택하고 실행하도록 설계할 수 있다.따라서 알고리즘의 시간 복잡성은 $O (VE 2$ )이다 $.$ ^[1]^[8]

예

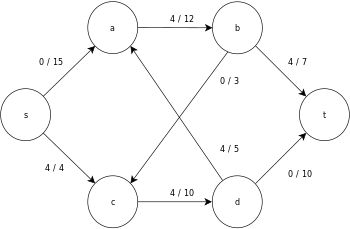
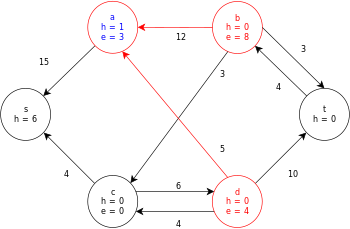
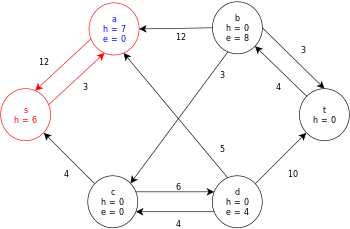
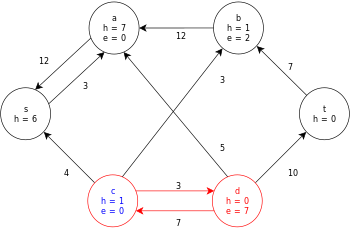
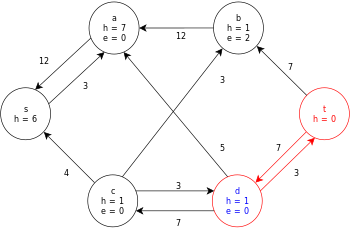
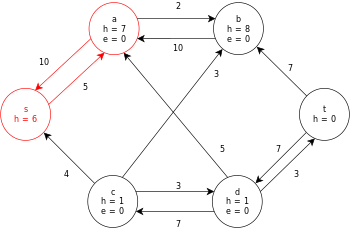
다음은 위에서 정의한 일반 푸시-릴라벨 알고리즘의 샘플 실행으로, 다음과 같은 간단한 네트워크 흐름 그래프 다이어그램이다.

초기 흐름 네트워크 그래프

최종 최대 흐름 네트워크 그래프

이 예에서 h와 e 값은 알고리즘 실행 중 노드의 라벨 $𝓁$ 과 $초과 f$ x 를 각각 나타낸다.예제의 각 잔차 그래프는 용량이 0보다 큰 잔차 호만 포함한다.각 잔차 그래프는 수행 작업 루프의 여러 반복을 포함할 수 있다.

알고리즘 작동	잔차 그래프
프리플로우를 값 0으로 설정하고 라벨링을 초기화하여 잔차 그래프를 초기화한다.
$초기$ 포화 푸시는 선원을 벗어난 모든 전유 호에서 수행된다.
노드 $a$ 는 초과 유량을 싱크대 $쪽$ 으로 밀기 위해 다시 부착된다. 이후 두 $번$ 의 포화 푸시 중 a에서의 초과분은 $b$ 로 밀리고 $d$ 로 밀리며, 이 경우 $a$ 는 다소 초과된다.

다시 한 번, $a$ 는 마지막 남은 양의 잔차를 따라 초과분을 밀어내기 위해 다시 붙여진다(즉, 초과분을 $다시$ s로 밀어넣기). 그런 다음 활성 노드 집합에서 노드 $a$ 를 제거한다.

Relabel $b$ 를 누른 다음 초과 값을 $t$ 와 $c$ 로 푸십시오.
Relabel c $그리고$ 그것의 초과분을 $d$ 로 밀어라.
Relabel d $그리고$ 그것의 초과분을 $t$ 로 밀어라.
이로써 노드 $b$ 는 유일하게 남아 있는 활성 노드로 남게 되지만, 초과 유량을 싱크대 쪽으로 밀어낼 수는 없다. Relabel $b$ 를 누른 다음 노드 $a$ 를 통해 초과분을 소스( $s$ ) 쪽으로 밀어 넣으십시오.

$마지막$ 남은 여분의 부분을 소스에 밀어 $넣으세요$ , s. 남아 있는 활성 노드가 없다.알고리즘은 그래프의 최대 흐름을 종료하고 반환한다(위 그림 참조).

예시(그러나 초기 흐름 0)는 여기서 대화식으로 실행할 수 있다.

실제 구현

일반적인 푸시-릴라벨 알고리즘에는 $O (VE 2)$ 시간 복잡성이 있지만, 효율적인 구현은 해당 푸시 및 리라벨 작동을 선택할 때 적절한 규칙을 시행함으로써 $O (V 3)$ 또는 더 낮은 시간 복잡성을 달성한다.경험적 성과는 휴리스틱스에 의해 더욱 개선될 수 있다.

"Current-arc" 데이터 구조 및 배출 작업

"current-arc" 데이터 구조는 정적 원형 순서에 따라 흐름 네트워크 노드의 내부 및 외부 인접부를 방문하기 위한 메커니즘이다.노드에 대해 단독으로 연결된 이웃 목록이 생성되면, 데이터 구조는 목록 안으로 들어가는 포인터처럼 간단할 수 있다.

"current-arc" 데이터 구조를 바탕으로 방전 연산을 정의할 수 있다.방출 작업은 활성 노드에 적용되며, 노드에서 흐름이 비활성화될 때까지 반복적으로 밀어내 프로세스에서 허용 가능한 호를 생성하기 위해 필요한 대로 다시 샘플링한다.

방전(u): 전류가 이웃[u]의 끝에서 떨어지면 x_f[u] > 0이 되고, reelabel(u) 전류가 되감기(u) 전류가 되감기(u)가 되감기(u, v)가 허용되면 push(u, v)가 u의 다음 이웃을 가리키도록 한다.

활성 노드 선택 규칙

방전 작동의 정의는 방전할 활성 노드를 반복적으로 선택하도록 푸시-릴라벨 알고리즘을 감소시킨다.선택 규칙에 따라 알고리즘은 다른 시간 복잡성을 나타낸다.간결성을 위해 우리는 다음 논의에서 노드를 언급할 때 $s$ 와 t를 무시한다.

FIFO 선택 규칙

FIFO 푸시-릴라벨 알고리즘은^[2] 활성 노드를 대기열로 구성한다.초기 활성 노드를 임의의 순서로 삽입할 수 있다.알고리즘은 항상 방전을 위해 대기열 전면에 있는 노드를 제거한다.비활성 노드가 활성화될 때마다 대기열 뒤쪽에 추가된다.

알고리즘은 $O (V 3)$ 시간의 복잡성을 가지고 있다.

재라벨 대 전면 선택 규칙

elabel-to-front push-elabel 알고리즘은^[1] 모든 노드를 링크된 목록으로 구성하고 허용 가능한 네트워크에 대해 목록이 토폴로지적으로 정렬된다는 불변성을 유지한다.알고리즘은 전방에서 후방까지 목록을 스캔하여 현재 노드가 활성 상태일 경우 방출 작업을 수행한다.노드가 다시 라벨링된 경우 목록 전면으로 이동하고 전면에서 스캔을 다시 시작한다.

알고리즘은 또한 $O (V 3)$ 시간 복잡성을 가지고 있다.

가장 높은 레이블 선택 규칙

가장 높은 라벨의 푸시-릴라벨 알고리즘은^[11] 모든 노드를 라벨에 의해 색인된 버킷으로 구성한다.알고리즘은 항상 가장 큰 라벨을 방출할 활성 노드를 선택한다.

알고리즘은 $O (V 2 (E)$ 시간 복잡성을 가지고 있다.가장 낮은 라벨 선택 규칙을 대신 사용하면 시간 복잡성이 $O (VE 2$ )가 된다 $.$ ^[3]

구현 기법

$위$ 의 일반적인 푸시-릴라벨 알고리즘의 설명에서 $((u)$ 는 처음부터 $s$ 와 $t$ 를 제외한 각 노드 u에 대해 0으로 설정되지만, 정확한 라벨을 계산하기 위해서는 $t$ 에서 역폭 우선 검색을 수행하는 것이 바람직하다.^[2]

알고리즘은 일반적으로 두 단계로 구분된다.1단계에서는 라벨이 $n$ 보다 낮은 활성 노드만 방출하여 최대 사전 흐름을 계산한다.2단계는 $t$ 에 도달할 수 없는 과잉 흐름을 $s$ 에 도달하지 못하는 초과 흐름을 되돌려 최대 전류를 최대 흐름으로 변환한다.2단계는 푸시 및 리라벨 작동 순서에 관계없이 $O (VE)$ 시간 복잡성을 가지며 따라서 1단계에 의해 지배된다는 것을 보여줄 수 있다.또는 흐름 분해를 이용하여 구현할 수 있다.^[9]

경험적 발견은 알고리즘의 경험적 성능을 향상시키는데 중요하다.^[12]일반적으로 사용되는 두 가지 휴리스틱스는 갭 휴리스틱과 글로벌 리마블링 휴리스틱이다.^[2]^[13]갭 휴리스틱은 라벨링 함수의 갭을 탐지한다. $𝓁(u)$ = $𝓁'$ 과 같은 노드 $u$ 가 없는 레이블 0 < 𝓁> < V가 있다면, $𝓁'$ < $𝓁(u)$ > $V$ 가 있는 노드 $u$ 는 $t$ 와 연결이 끊어져 즉시 $(V$ + 1)로 다시 라벨을 붙일 수 있다.글로벌 리빌링 휴리스틱은 노드의 정확한 라벨을 계산하기 위해 $G$ 의_f $t$ 에서 후진 너비 우선 검색을 주기적으로 수행한다.두 가지 휴리스틱스 모두 도움이 되지 않는 리라벨 연산을 생략하는데, 이는 알고리즘의 병목현상이며 동적 트리의 비효과성에 기여한다.^[4]

샘플 구현

C 구현

#include <stdlib.h> #include <stdio.h>  #NODE 6 정의 #Define MIN(X,Y) (X) < (Y) ? (X) : (Y) #인피니트 10000000 정의  공허하게 하다 밀다(경시하다 인트로 * 경시하다 * C, 인트로 ** F, 인트로 *과잉의, 인트로 u, 인트로 v) {   인트로 보내다 = 분(과잉의[u], C[u][v] - F[u][v]);   F[u][v] += 보내다;   F[v][u] -= 보내다;   과잉의[u] -= 보내다;   과잉의[v] += 보내다; }  공허하게 하다 라벨을 다시 붙이다(경시하다 인트로 * 경시하다 * C, 경시하다 인트로 * 경시하다 * F, 인트로 *높이, 인트로 u) {   인트로 v;   인트로 min_min = 인피니트;   을 위해 (v = 0; v < 노드; v++) {     만일 (C[u][v] - F[u][v] > 0) {       min_min = 분(min_min, 높이[v]);       높이[u] = min_min + 1;     }   } };  공허하게 하다 방류하다(경시하다 인트로 * 경시하다 * C, 인트로 ** F, 인트로 *과잉의, 인트로 *높이, 인트로 *보이는, 인트로 u) {   하는 동안에 (과잉의[u] > 0) {     만일 (보이는[u] < 노드) {       인트로 v = 보이는[u];       만일 ((C[u][v] - F[u][v] > 0) && (높이[u] > 높이[v])) {         밀다(C, F, 과잉의, u, v);       } 다른 {         보이는[u] += 1;       }     } 다른 {       라벨을 다시 붙이다(C, F, 높이, u);       보이는[u] = 0;     }   } }  공허하게 하다 전면으로 이동(인트로 i, 인트로 *A) {   인트로 임시 변통하다 = A[i];   인트로 n;   을 위해 (n = i; n > 0; n--) {     A[n] = A[n-1];   }   A[0] = 임시 변통하다; }  인트로 푸시렐라벨(경시하다 인트로 * 경시하다 * C, 인트로 ** F, 인트로 출처, 인트로 가라앉다) {   인트로 *과잉의, *높이, *리스트를 작성하다, *보이는, i, p;    과잉의 = (인트로 *) 칼록(노드, 의 크기(인트로));   높이 = (인트로 *) 칼록(노드, 의 크기(인트로));   보이는 = (인트로 *) 칼록(노드, 의 크기(인트로));    리스트를 작성하다 = (인트로 *) 칼록((노드-2), 의 크기(인트로));    을 위해 (i = 0, p = 0; i < 노드; i++){     만일 ((i != 출처) && (i != 가라앉다)) {       리스트를 작성하다[p] = i;       p++;     }   }    높이[출처] = 노드;   과잉의[출처] = 인피니트;   을 위해 (i = 0; i < 노드; i++)     밀다(C, F, 과잉의, 출처, i);    p = 0;   하는 동안에 (p < 노드 - 2) {     인트로 u = 리스트를 작성하다[p];     인트로 old_properties = 높이[u];     방류하다(C, F, 과잉의, 높이, 보이는, u);     만일 (높이[u] > old_properties) {       전면으로 이동(p, 리스트를 작성하다);       p = 0;     } 다른 {       p += 1;     }   }   인트로 최대 흐름 = 0;   을 위해 (i = 0; i < 노드; i++)     최대 흐름 += F[출처][i];    무료의(리스트를 작성하다);    무료의(보이는);   무료의(높이);   무료의(과잉의);    돌아오다 최대 흐름; }  공허하게 하다 프린트매트릭스(경시하다 인트로 * 경시하다 * M) {   인트로 i, j;   을 위해 (i = 0; i < 노드; i++) {     을 위해 (j = 0; j < 노드; j++)       활자화하다("%d\t",M[i][j]);     활자화하다("\n");   } }  인트로 본래의(공허하게 하다) {   인트로 **흐르다, **역량, i;   흐르다 = (인트로 **) 칼록(노드, 의 크기(인트로*));   역량 = (인트로 **) 칼록(노드, 의 크기(인트로*));   을 위해 (i = 0; i < 노드; i++) {     흐르다[i] = (인트로 *) 칼록(노드, 의 크기(인트로));     역량[i] = (인트로 *) 칼록(노드, 의 크기(인트로));   }    // 샘플 그래프   역량[0][1] = 2;   역량[0][2] = 9;   역량[1][2] = 1;   역량[1][3] = 0;   역량[1][4] = 0;   역량[2][4] = 7;   역량[3][5] = 7;   역량[4][5] = 4;    활자화하다("용량:\n");   프린트매트릭스(역량);    활자화하다("최대 흐름:\n%d\n", 푸시렐라벨(역량, 흐르다, 0, 5));    활자화하다("흐름:\n");   프린트매트릭스(흐르다);    돌아오다 0; }

파이썬 구현

반항하다 reelabel_to_front(C, 출처: 인트로, 가라앉다: 인트로) -> 인트로:     n = 렌(C)  # C는 용량 매트릭스     F = [[0] * n 을 위해 _ 에 범위(n)]     # u에서 v까지의 잔류 용량은 C[u][v] - F[u][v]      높이 = [0] * n  # 노드의 높이     과잉의 = [0] * n  # 노드로의 흐름 - 노드에서 흐름 제외     보이는   = [0] * n  # 마지막 리라벨 이후 보이는 이웃들     # 노드 "노드"     노들리스트 = [i 을 위해 i 에 범위(n) 만일 i != 출처 그리고 i != 가라앉다]      반항하다 밀다(u, v):         보내다 = 분(과잉의[u], C[u][v] - F[u][v])         F[u][v] += 보내다         F[v][u] -= 보내다         과잉의[u] -= 보내다         과잉의[v] += 보내다      반항하다 라벨을 다시 붙이다(u):         # 밀기 가능케 하는 가장 작은 새 키를 찾아라.         # 그런 추진이 조금이라도 가능하다면.         min_min = ∞         을 위해 v 에 xrange(n):             만일 C[u][v] - F[u][v] > 0:                 min_min = 분(min_min, 높이[v])                 높이[u] = min_min + 1      반항하다 방류하다(u):         하는 동안에 과잉의[u] > 0:             만일 보이는[u] < n:  # 다음 이웃 확인                 v = 보이는[u]                 만일 C[u][v] - F[u][v] > 0 그리고 높이[u] > 높이[v]:                     밀다(u, v)                 다른:                     보이는[u] += 1             다른:  # 우리는 모든 이웃을 확인했다. 다시 라벨을 붙여야 한다.                 라벨을 다시 붙이다(u)                 보이는[u] = 0      높이[출처] = n  # 소스에서 싱크까지 가장 긴 경로가 n보다 작음     과잉의[출처] = ∞  # 가능한 한 많은 흐름을 근린에게 보낸다.     을 위해 v 에 범위(n):         밀다(출처, v)      p = 0     하는 동안에 p < 렌(노들리스트):         u = 노들리스트[p]         old_properties = 높이[u]         방류하다(u)         만일 높이[u] > old_properties:             노들리스트.삽입하다(0, 노들리스트.펑펑 터지다(p))  # 리스트 앞으로 이동             p = 0  # 명단에서 출발         다른:             p += 1      돌아오다 합계를 내다(F[출처])

참조

^ ^a ^b ^c Cormen, T. H.; Leiserson, C. E.; Rivest, R. L.; Stein, C. (2001). "§26 Maximum flow". Introduction to Algorithms (2nd ed.). The MIT Press. pp. 643–698. ISBN 978-0262032933.
^ ^a ^b ^c ^d ^e ^f ^g Goldberg, A V; Tarjan, R E (1986). "A new approach to the maximum flow problem". Proceedings of the eighteenth annual ACM symposium on Theory of computing – STOC '86. p. 136. doi:10.1145/12130.12144. ISBN 978-0897911931. S2CID 14492800.
^ ^a ^b Ahuja, Ravindra K.; Kodialam, Murali; Mishra, Ajay K.; Orlin, James B. (1997). "Computational investigations of maximum flow algorithms". European Journal of Operational Research. 97 (3): 509. CiteSeerX 10.1.1.297.2945. doi:10.1016/S0377-2217(96)00269-X.
^ ^a ^b ^c Goldberg, Andrew V. (2008). "The Partial Augment–Relabel Algorithm for the Maximum Flow Problem". Algorithms – ESA 2008. Lecture Notes in Computer Science. Vol. 5193. pp. 466–477. CiteSeerX 10.1.1.150.5103. doi:10.1007/978-3-540-87744-8_39. ISBN 978-3-540-87743-1.
^ Goldberg, Andrew V (1997). "An Efficient Implementation of a Scaling Minimum-Cost Flow Algorithm". Journal of Algorithms. 22: 1–29. doi:10.1006/jagm.1995.0805.
^ Ahuja, Ravindra K.; Orlin, James B. (1991). "Distance-directed augmenting path algorithms for maximum flow and parametric maximum flow problems". Naval Research Logistics. 38 (3): 413. CiteSeerX 10.1.1.297.5698. doi:10.1002/1520-6750(199106)38:3<413::AID-NAV3220380310>3.0.CO;2-J.
^ Goldberg, Andrew V.; Tarjan, Robert E. (2014). "Efficient maximum flow algorithms". Communications of the ACM. 57 (8): 82. doi:10.1145/2628036. S2CID 17014879.
^ ^a ^b ^c ^d Goldberg, Andrew V.; Tarjan, Robert E. (1988). "A new approach to the maximum-flow problem". Journal of the ACM. 35 (4): 921. doi:10.1145/48014.61051. S2CID 52152408.
^ ^a ^b Ahuja, R. K.; Magnanti, T. L.; Orlin, J. B. (1993). Network Flows: Theory, Algorithms, and Applications (1st ed.). Prentice Hall. ISBN 978-0136175490.
^ Shiloach, Yossi; Vishkin, Uzi (1982). "An O(n2log n) parallel max-flow algorithm". Journal of Algorithms. 3 (2): 128–146. doi:10.1016/0196-6774(82)90013-X.
^ Cheriyan, J.; Maheshwari, S. N. (1988). "Analysis of preflow push algorithms for maximum network flow". Foundations of Software Technology and Theoretical Computer Science. Lecture Notes in Computer Science. Vol. 338. p. 30. doi:10.1007/3-540-50517-2_69. ISBN 978-3-540-50517-4.
^ Cherkassky, Boris V.; Goldberg, Andrew V. (1995). "On implementing push-relabel method for the maximum flow problem". Integer Programming and Combinatorial Optimization. Lecture Notes in Computer Science. Vol. 920. p. 157. CiteSeerX 10.1.1.150.3609. doi:10.1007/3-540-59408-6_49. ISBN 978-3-540-59408-6.
^ Derigs, U.; Meier, W. (1989). "Implementing Goldberg's max-flow-algorithm ? A computational investigation". ZOR Zeitschrift für Operations Research Methods and Models of Operations Research. 33 (6): 383. doi:10.1007/BF01415937. S2CID 39730584.

[clrs26-1] Cormen, T. H.; Leiserson, C. E.; Rivest, R. L.; Stein, C. (2001). "§26 Maximum flow". Introduction to Algorithms (2nd ed.). The MIT Press. pp. 643–698. ISBN 978-0262032933.

[goldberg86-2] ^ ^a ^b ^c ^d ^e ^f ^g Goldberg, A V; Tarjan, R E (1986). "A new approach to the maximum flow problem". Proceedings of the eighteenth annual ACM symposium on Theory of computing – STOC '86. p. 136. doi:10.1145/12130.12144. ISBN 978-0897911931. S2CID 14492800.

[ahuja97-3] Ahuja, Ravindra K.; Kodialam, Murali; Mishra, Ajay K.; Orlin, James B. (1997). "Computational investigations of maximum flow algorithms". European Journal of Operational Research. 97 (3): 509. CiteSeerX 10.1.1.297.2945. doi:10.1016/S0377-2217(96)00269-X.

[goldberg08-4] Goldberg, Andrew V. (2008). "The Partial Augment–Relabel Algorithm for the Maximum Flow Problem". Algorithms – ESA 2008. Lecture Notes in Computer Science. Vol. 5193. pp. 466–477. CiteSeerX 10.1.1.150.5103. doi:10.1007/978-3-540-87744-8_39. ISBN 978-3-540-87743-1.

[goldberg97-5] Goldberg, Andrew V (1997). "An Efficient Implementation of a Scaling Minimum-Cost Flow Algorithm". Journal of Algorithms. 22: 1–29. doi:10.1006/jagm.1995.0805.

[ahuja91-6] Ahuja, Ravindra K.; Orlin, James B. (1991). "Distance-directed augmenting path algorithms for maximum flow and parametric maximum flow problems". Naval Research Logistics. 38 (3): 413. CiteSeerX 10.1.1.297.5698. doi:10.1002/1520-6750(199106)38:3<413::AID-NAV3220380310>3.0.CO;2-J.

[goldberg2014-7] Goldberg, Andrew V.; Tarjan, Robert E. (2014). "Efficient maximum flow algorithms". Communications of the ACM. 57 (8): 82. doi:10.1145/2628036. S2CID 17014879.

[goldberg88-8] Goldberg, Andrew V.; Tarjan, Robert E. (1988). "A new approach to the maximum-flow problem". Journal of the ACM. 35 (4): 921. doi:10.1145/48014.61051. S2CID 52152408.

[amo93-9] Ahuja, R. K.; Magnanti, T. L.; Orlin, J. B. (1993). Network Flows: Theory, Algorithms, and Applications (1st ed.). Prentice Hall. ISBN 978-0136175490.

[sv82-10] Shiloach, Yossi; Vishkin, Uzi (1982). "An O(n2log n) parallel max-flow algorithm". Journal of Algorithms. 3 (2): 128–146. doi:10.1016/0196-6774(82)90013-X.

[cheriyan88-11] Cheriyan, J.; Maheshwari, S. N. (1988). "Analysis of preflow push algorithms for maximum network flow". Foundations of Software Technology and Theoretical Computer Science. Lecture Notes in Computer Science. Vol. 338. p. 30. doi:10.1007/3-540-50517-2_69. ISBN 978-3-540-50517-4.

[cherkassky95-12] Cherkassky, Boris V.; Goldberg, Andrew V. (1995). "On implementing push-relabel method for the maximum flow problem". Integer Programming and Combinatorial Optimization. Lecture Notes in Computer Science. Vol. 920. p. 157. CiteSeerX 10.1.1.150.3609. doi:10.1007/3-540-59408-6_49. ISBN 978-3-540-59408-6.

[derigs89-13] Derigs, U.; Meier, W. (1989). "Implementing Goldberg's max-flow-algorithm ? A computational investigation". ZOR Zeitschrift für Operations Research Methods and Models of Operations Research. 33 (6): 383. doi:10.1007/BF01415937. S2CID 39730584.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[10]

[11]

[9]

[12]

[13]

Search