결정계수

이 기사는 독일어로 된 해당 기사에서 번역된 텍스트로 확장될 수 있습니다.【2019년 9월】중요한 번역에 대해서는,［show］를 클릭해 주세요. 독일어 문서의 기계 번역 버전을 봅니다. DeepL이나 Google Translate 등의 기계번역은 번역의 시작점이 됩니다.단, 번역자는 기계번역 텍스트를 영어 위키피디아에 복사하여 붙여넣는 것이 아니라 필요에 따라 오류를 수정하고 번역이 정확한지 확인해야 합니다. 이 템플릿에 토픽을 추가하는 것을 검토해 주십시오.메인 카테고리에는 이미 9,370개의 기사가 있으며, topic=분류에 도움이 됩니다. 신뢰할 수 없거나 품질이 낮은 텍스트는 번역하지 마십시오.가능하면 외국어로 된 기사에 기재된 참고문헌을 사용하여 본문을 확인합니다. 번역원과의 언어 간 링크를 제공하여 번역과 함께 편집 요약에 저작권 속성을 입력해야 합니다.모델 속성 편집 요약은 다음과 같습니다.Content in this edit is translated from the existing German Wikipedia article at [[:de:Bestimmtheitsmaß]]; see its history for attribution. 템플릿도 추가해야 합니다.{{Translated de Bestimmtheitsmaß}}토크 페이지로 이동합니다. 자세한 내용은 Wikipedia를 참조하십시오.번역.

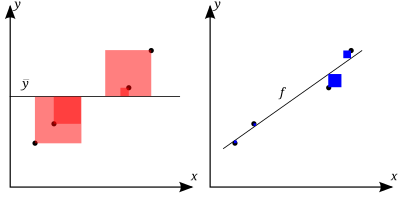
통계학에서 결정계수는 R 또는 r로² 표시되고² "R 제곱"으로 발음되며 독립 변수에서 예측 가능한 종속 변수의 변동 비율이다.

기타 관련 정보에 기초한 미래 결과의 예측 또는 가설의 테스트가 주된 목적인 통계 모델의 맥락에서 사용되는 통계량이다.모형에 ^[1][2][3]의해 설명되는 결과의 총 변동 비율을 기반으로 모형에 의해 관찰된 결과가 얼마나 잘 복제되는지에 대한 측정값을 제공합니다.

R에 대한 정의는² 몇 가지이며, 이는 때때로 동등합니다.이러한 사례의 한 클래스는 R 대신² r을² 사용하는 단순 선형 회귀 분석을 포함합니다.절편만 포함된 경우² r은 단순히 관측 결과와 관측 예측 변수 ^[4]값 사이의 표본 상관 계수(즉, r)의 제곱입니다.추가 회귀 변수가 포함된 경우 R은 다중² 상관 계수의 제곱입니다.두 경우 모두 결정 계수는 일반적으로 0부터 1까지입니다.

사용된 정의에 따라 R의 계산² 정의가 음의 값을 산출할 수 있는 경우가 있습니다.이는 해당 결과와 비교되는 예측이 해당 데이터를 사용한 모형 적합 절차에서 도출되지 않은 경우에 발생할 수 있습니다.모형 적합 절차를 사용했더라도 R은² 예를 들어 ^[5]절편을 포함하지 않고 선형 회귀를 수행하거나 비선형 함수를 사용하여 데이터를 ^[6]적합시키는 경우 여전히 음수일 수 있습니다.음수 값이 발생하는 경우 데이터의 평균이 이 특정 기준에 따라 적합 함수 값보다 결과에 더 잘 적합됩니다.

결정 계수는 회귀 분석 평가에서 MAE, MAPE, MSE 및 RMSE보다 (직관적으로) 더 유익할 수 있다. 전자는 백분율로 표현될 수 있지만 후자는 임의 범위를 갖는다.또한 ^[7]기사에서 테스트 데이터셋의 SMAPE와 비교하여 불량 적합성에 대해 더 강력하다는 것이 입증되었다.

시뮬레이션(Y_pred) 대 측정된(Y_obs) 값의 적합도를 평가할 때 선형 회귀(예: Y_obs= m·Y_pred + b)^{[citation needed]}의 R에² 기초하는 것은 적절하지 않다.R은² Y와_pred Y 사이의_obs 선형 상관의 정도를 수량화하는 반면 적합도 평가에서는 다음과 같은 하나의 특정 선형 상관만 고려해야 합니다.Y_obs = 1·Y_pred + 0(1:1 ^[8][9]라인).

정의들

데이터 세트는 y,...y_n(총칭하여 y 또는_i 벡터 y = [y₁, ...y_nn])^T로 표시된₁ n개의 값을 가지며, 각각은 적합(또는 모델링 또는 예측) 값₁ f,..., f(또는_i 때로는 θ_i, 벡터 f)와 관련지어집니다.

잔차를 e = y_i - f_i(벡터 e 형성)로_i 정의합니다.

y$(\$가 관측된 데이터의 평균인 $경우{\displaystyle \stackrel{}{}}$:

데이터 세트의 변동성은 두 제곱 공식으로 측정할 수 있습니다.

• 잔차 제곱합이라고도 하는 잔차 제곱합:
  $${\displaystyle SS_{\text{res}}=\sum _{i}(y_{i}-f_{i})^{2}=\sum _{i}e_{i}^2},}$$

  
• 총 제곱합(데이터 분산에 비례함):
  $${\displaystyle SS_{\text{tot}}=\sum _{i}(y_{i}-{\bar {y})^{2}}$$

  

결정 계수의 가장 일반적인 정의는 다음과 같다.

최상의 경우 모델링된 값이 관측된 값과 정확히 일치하므로 ${\displaystyle {}_{}}$ ${\displaystyle {\text{res}}_{}}$ $=$ {\$displaystyle SS_$${\$$text{$$res$}}=$0$$}$ 및$$ $R{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ $=$ {\$displaystyle$$$R$^{2$$}=$$1}$이 됩니다. 항상 $y$를 $예측$하는 기준선 모델은 ${\displaystyle {R\mathrm{}}^{}}$ $0style$ R = 0style $R2$입니다.이 기준선보다 나쁜 예측은 음의 $({$ R$^{2$가 됩니다.

원인 불명의 분산과의 관계

두 번째 항은 설명할 수 없는 분산(모델 오류의 분산)을 총 분산(데이터의)과 비교하기 때문에 일반적인 형태에서 R은 설명할² 수 없는 분산 비율(FVU)과 관련이 있는 것으로 볼 수 있다.

설명한 바와 같이 분산

R = 0.49라고 가정합니다².이는 데이터 집합에서 종속 변수의 변동성의 49%가 설명되었고 나머지 51%는 여전히 설명되지 않았다는 것을 의미한다.회귀 모형의 경우 설명되는 제곱합이라고도 하는 회귀 제곱합은 다음과 같이 정의됩니다.

${\displaystyle SS_{\text{reg}}=\sum _{i}(f_{i}-{\bar {y})^{2}}$

경우에 따라 단순 선형 회귀 분석에서처럼 총 제곱합은 위에서 정의한 다른 두 제곱합과 같습니다.

$\displaystyle SS_{\text{res}}+SS_{\text{reg}}=SS_{\text{tot}}}$

관계가 유지되는 한 경우에 대한 이 결과의 도출에 대해서는 일반 OLS 모델의 분할을 참조하십시오.이 관계가 유지되면 위의 R의 정의는² 다음과 같습니다.

${\displaystyle R^{2}=syslogfrac {SS_{\text{reg}}}{SS_{\text{tot}}}}=syslogfrac {SS_{\text{reg}}/n}{SS_{\text{tot}}/n}}}$

여기서 n은 변수에 대한 관측치(사례) 수입니다.

이 형식에서² R은 전체 분산(의존 변수의 표본 분산, 즉 SS_regtot/n)에 대한 설명 분산(모형 예측의 분산)의 비율로 표현됩니다.

예를 들어 선형 회귀 분석을 통해 모형 값 θ를_i 얻은 경우 제곱합에 대한 이 분할은 고정됩니다.보다 가벼운 상태는 다음과 같습니다.모델은 다음과 같은 형태를 가지고 있다.

${\displaystyle f_{i}=와이드햇 {\widehat}q_{i},$

여기서_i q는 i 또는 기타 자유 매개변수에 의존하거나 의존하지 않을 수 있는 임의의 값(일반 선택_i q_i = x는 특별한 경우일 뿐)이며 계수 $^$ $및$ β $^${\$widehat }$은 제곱합$$ 최소화를 통해 구한다.

이 조건 집합은 중요한 조건이며 적합 잔차 및 모형화된 값의 속성에 여러 가지 영향을 미칩니다.특히, 이러한 조건에서는, 다음과 같이 됩니다.

$({displaystyle {f}}=바 {y}},}$

As 제곱 상관 계수

추정 절편 항이 있는 선형 최소 제곱 다중 회귀 분석에서 R은² $관측$된$$y {\$displaystyle$ y$}$와 종속 변수의 모델링$($예측) $f{\displaystyle }$ {\$displaystyle$ f$}$ 데이터$$ 값 사이의 Pearson 상관 계수의 제곱과 같습니다.

절편 항과 단일 설명자를 사용한 선형 최소 제곱 회귀 분석에서는 $종속{\displaystyle }$ 변수$$y$및$ $설명{\displaystyle }$ 변수${\displaystyle }$x의$$ Pearson 상관 계수의 제곱과도 같습니다$.$ {\$displaystyle$ x$}$

다음과 같이 정의된 두 설명 변수 간의 상관 계수와 혼동해서는 안 된다.

$\displaystyle \rho _{\widehat }, {\widehat }, {\widehat }, {\widehat }, {\widehat }, {\widehat }, {\widehat }, {\widehat }}, {\widehat },$

여기서 두 계수 추정치 사이의 공분산 및 표준 편차는 계수 추정치의 공분산 행렬에서 구한다$.{\displaystyle }$ (${\displaystyle X^{}}$ ${\displaystyle {}^{}{}^{}}$X${\displaystyle {}^{}}$) - ${\displaystyle 1^{}}${{$Displaystyle (X^{T}X)^{-1$

선형 최소 제곱 회귀 분석과 다른 모델에서 예측 값이 생성될 수 있는 보다 일반적인 모델링 조건에서는 R $값$은 원래²$$y$데이터$ 값과 $모델링된{\displaystyle }$f $데이터$ 값 사이의 상관 계수의 제곱으로 계산할 수 있습니다.이 경우, 값은 모델링된 값이 얼마나 좋은지에 대한 직접적 측정이 아니라 모델링된 값에서 얼마나 좋은 예측 변수를 구성할 수 있는지에 대한 측정값이다(α + β_i ^{[citation needed]}β 형식의 수정된 예측 변수를 생성함).에버릿에 따르면,^[10] 이 용도는 특히 "결정 계수"라는 용어의 정의입니다. 즉, 두 변수 사이의 상관 관계 제곱입니다.

해석

R은^{2 [11]}모형의 적합도에 대한 측도입니다.회귀² 분석에서 R 결정 계수는 회귀 예측이 실제 데이터 점에 얼마나 잘 근접하는지 나타내는 통계적 측도입니다.R이 1이면 회귀² 예측이 데이터에 완벽하게 적합함을 나타냅니다.

0 ~ 1 범위를 벗어난 R 값은² 모형이 가능한 최악의 최소 제곱 예측 변수(관측 데이터의 평균과 동일한 높이의 수평 초평면과 동일)보다 더 나쁜 데이터를 적합시킬 때 발생합니다.이는 잘못된 모형을 선택했거나 의미 없는 제약 조건이 실수로 적용된 경우에 발생합니다.Kvolseth의^[12] 방정식 1을 사용할 경우(이것이 가장 자주 사용되는 방정식), R은² 0보다 작을 수 있습니다.Kvolseth의 식 2를 사용하면 R은² 1보다 클 수 있다.

R을 사용하는 모든² 경우 예측 변수는 일반 최소 제곱 회귀 분석, 즉 SS를 최소화하여_res 계산됩니다.이² 경우 모형의 변수 수가 증가할수록 R이 증가합니다²(R은 포함된 변수 수에 따라 단조 증가함. 절대 감소하지 않음).이는 R 값을 증가시키기² 위해 변수를 계속 추가할 수 있는(주방 싱크 회귀) R을 사용할² 수 있는 단점을 보여준다.예를² 들어, 자동차의 연비, 가격, 엔진 출력으로 모델의 판매를 예측하려는 경우, R은 변수가 추가될수록 감소하지 않고 증가하기 때문에 모델 이름의 첫 글자 또는 자동차를 설계하는 책임 엔지니어의 키와 같은 관련 없는 요소를 포함할 수 있다.e는 우연에 의한 것입니다.

이는² 조정된 R을 검토하는 대안적 접근법으로 이어진다.이 통계량의 설명은 R과 거의² 동일하지만 모형에 추가 변수가 포함되므로 통계량에 불이익을 줍니다.일반 최소 제곱에 의한 적합을 제외한 경우에는 위와 같이² R 통계량을 계산할 수 있으며 여전히 유용한 측도가 될 수 있습니다.적합이 가중 최소 제곱 또는 일반화 최소 제곱에 의해 이루어지는 경우, R의 대체² 버전은 통계 프레임워크에 적합하게 계산될 수 있으며, "원시²" R은 더 쉽게 해석될 경우 여전히 유용할 수 있다.R에 대한 값은² 통계적 근거를 가질 필요가 없는 모든 유형의 예측 모델에 대해 계산할 수 있습니다.

다중 선형 모형에서

두 개 이상의 설명 변수가 있는 형식의 선형 모형 고려

${\displaystyle Y_{i}=\beta _{0}+\sum _{j=1}^{p}\sum _{j}X_{i,j}+\varepsilon _{i}$

여기서 ih의 경우$(\displaystyle$ {$Y_{$i})는 응답 변수${\displaystyle {}_{}}$ ${\displaystyle {\mathrm{Xi}}_{},{Xi,}_{}}$ $(\$는 회귀 변수, ${\displaystyle i_{}}$i(\$displaystyle \varepsilon_i,p})$는 평균 오류 용어입니다.${\displaystyle {\beta \mathrm{}}_{}}$ 0${\displaystyle ,}$ ${\displaystyle \dots ,}$ ${\displaystyle {\beta }_{}}$p \$displaystyle \beta$ _${0},\dots,\beta$ _${p}$의 양은 최소 제곱으로 추정되는 미지의 계수이다.결정² 계수 R은 모형의 전역 적합도에 대한 측도입니다.특히 R은² [0, 1]의 원소이며 ^[13]X의 회귀 변수(해명 변수)의 선형 조합에 기인할 수 있는 Y의_i 변동 비율을 나타냅니다.

R은² 종종 모형의 회귀 분석기가 "설명하는" 반응 변동의 비율로 해석됩니다.반면 R2=0이 응답 변수 사이에 regres이 없'linear의 관계(직선 회귀에, 이는 직선 모델은 일정한 라인(비탈)0, 요격)y¯{\displaystyle{\bar{y}}}를 의미한다)여부를 나타내는 그러므로, R2=1이 장착된 모델은 y{이\displaystyle}의 모든 가변성을 설명할 것임을 나타낸다.sors) R = 0.7과 같은² 내부 값은 다음과 같이 해석할 수 있습니다. "반응 변수의 분산 중 7퍼센트는 설명 변수에 의해 설명될 수 있습니다.나머지 30%는 알려지지 않은 숨은 변수 또는 내재된 변동성에 기인할 수 있습니다."

상관관계와 연관성에 대한 다른 통계적 설명과 마찬가지로 R에 적용되는² 주의사항은 "상관관계가 인과관계를 의미하지 않는다"는 것이다.즉, 상관관계가 때로는 변수 간의 인과관계를 밝혀내는 데 귀중한 단서를 제공할 수 있지만, 두 변수 간의 추정 상관관계 자체가 한 변수의 값을 변경하는 것이 다른 변수의 값을 변화시킨다는 증거는 아니다.예를 들어, 성냥(또는 라이터)을 휴대하는 관행은 폐암 발병률과 관련이 있지만, 성냥을 휴대하는 것은 암을 유발하지 않는다(표준적인 의미의 "원인").

최소 제곱으로 적합된 단일 회귀 분석기의 경우 R은² 회귀 분석기와 반응 변수와 관련된 Pearson 곱-모멘트 상관 계수의 제곱입니다.일반적으로 R은 생성된² 예측 변수와 반응 변수 사이의 상관 관계 제곱입니다.두 개 이상의 회귀기를 사용하는 경우, R은² 다중 결정 계수라고 할 수 있습니다.

R의 인플레이션²

일반적인 데이터를 사용하는 제곱법에서 R은² 모형의 회귀 변수 수가 증가함에 따라 최소한 약하게 증가합니다.회귀 분석기의 수가 증가하면 R의 값이² 증가하므로 R만으로는² 독립 변수의 수가 매우 다른 모형을 유의하게 비교할 수 없습니다.두 모형 간의 의미 있는 비교를 위해 잔차 제곱합에^{[citation needed]} 대해 F-검정을 수행할 수 있습니다. 이는 그레인저 인과 관계의 F-검정과 유사하지만 항상 적절한^{[further explanation needed]} 것은 아닙니다.이를 상기시키기 위해 일부 저자는 R by_q² R을 나타내며², 여기서 q는 X의 열 수(상수를 포함한 설명자의 수)이다.

이 특성을 입증하기 위해 먼저 최소 제곱 선형 회귀 분석의 목적은 다음과 같습니다.

${\displaystyle\min_{b}SS_{\text{res}}}(b)\오른쪽 화살표 \min _{b}\sum _{i}(y_{i}-X_{i}b)^{2},}$

여기서_i X는 사례 i에 대한 설명 변수 값의 행 벡터이고 b는 X의_i 각 원소의 계수 열 벡터이다.

더 많은 설명 변수가 추가될수록 목표의 최적 값은 약하게 작아지고, 따라서 X$(IH$ 행이 X인_i 설명 데이터 매트릭스)$$의 추가 열이 추가된다. 이는 제약이 적은 최소화가 더 적은 최소화보다 약하게 적은 최적 비용으로 이어지기 때문이다.앞의 결론에 따라 ${\displaystyle {SS}_{}}$ t$$ \ $displaystyle SS_{$tot$}$는 y에만 의존한다는 $점$에 유의하여 R의² 비감소 특성은 위의 정의에서 직접 나타난다.

추가 설명 변수를 사용하여 R을² 낮출 수 없는 직관적인 이유는 다음과 같습니다.$SS$$res$를 $최소화$하는 것은 R을 최대화하는² 것과 같습니다$.$추가 변수가 포함된 경우 데이터는 항상 예측 계수를 0으로 설정하고 예측 값과 R은² 변경하지 않는 옵션을 제공합니다.최적화 문제가 0이 아닌 계수를 제공하는 유일한 방법은 R이² 개선되는 것입니다.

주의사항

R은² 다음 사항을 나타내지 않습니다.

• 독립 변수는 종속 변수 변화의 원인이다.
• 생략-소수편향이 존재한다.
• 올바른 회귀 분석을 사용했다.
• 가장 적절한 독립 변수 세트가 선택되었다.
• 설명 변수에 대한 데이터에 공선성이 존재한다.
• 기존 독립 변수 세트의 변환 버전을 사용하여 모델을 개선할 수 있다.
• 확실한 결론을 내리기에 충분한 데이터 포인트가 있습니다.

내선번호

조정된² R

한 조정 R2의 사용(하나의 공통 표기법은 R¯ 2{\displaystyle{\bar{R}}^{2}}, 발음"R바 없겠다"; 다른 하나는 R은 2{\displaystyle R_{\text{}}^{2}}또는 Radj 2{\displaystyle R_{\text{adj}}^{2}})은 시도가 R2의 현상 시 자동으로 추가 e. 책임 지고에)언어 변수가 모델에 추가됩니다.()^[14]을 조정하는 방법은 여러 가지가 있습니다.지금까지 가장 많이 사용된 것은 보통 수정 R이라고 불릴 정도로 Mordecai Ezekiel이 ^[14][15]제안한 보정이다.조정된² R은 다음과 같이 정의됩니다.

${\displaystyle {R}^{2}={1-{SS_{\text{res}}/{\text{df}}_{\text{res}}\over SS_{\text{tot}}}/{\text{tot}}}}}}$

모델 수 차이의 견적의 자유 어디 dfres은도이고 모 분산의 견적의 비열하다. dfres에 자유의 dftot은도 샘플 크기 n및 변수의 모델에서 수, dfres =n-p 말이죠 dftot의 방법과 동일하지만 p고 단위가 주어질 경우 주어진다.평균에 y,즉_tot, df = n-1.

자유도를 삽입하고 R^2의 정의를 사용하여 다음과 같이 다시 작성할 수 있습니다.

$({displaystyle {R}}^{2}=1-(1-R^{2}){n-1 \over n-p})$

여기서 p는 모형에 포함된 설명 변수의 총 개수이고 n은 표본 크기입니다.

수정된² R은 음수일 수 있으며 값은 항상 R보다² 작거나 같습니다.R과 달리², 수정된² R은 (새로운 설명 변수를 포함함으로써) R의² 증가가 우연히 볼 수 있는 것보다 클 때만 증가한다.매번 계산된 조정된² R을 사용하여 미리 결정된 중요도 계층을 갖는 일련의 설명 변수를 한 번에 하나씩 회귀 분석으로 도입한다면, 조정된² R이 최대치에 도달하고 이후 감소하는 수준은 초과/불필요한 용어 없이 최적의 조합을 갖는 이상적인 회귀가 될 것이다.

수정된² R은 모집단² R의 덜 치우친 추정치로 해석될 수 있는 반면 관측된 표본² R은 모집단 값의 ^[16]양의 치우친 추정치입니다.수정² R은 모형 적합도(독립 변수에 의해 설명되는 종속 변수의 분산)를 평가하고 모형 ^[16]구축의 특징 선택 단계에서 대체 모형을 비교할 때 더 적합합니다.

조정된² R 통계량의 원리는 일반² R을 다음과 같이 고쳐 쓰면 알 수 있다.

${\displaystyle R^{2}={1-{\textit {VAR}_{\text{res}}\over {\textit {VAR}}_{\text{tot}}}}$

${\displaystyle {\text{여기}}_{}}$서 ${\displaystyle {\text{VAR}}_{}}$ res ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{\text{res}}_{}}$ /$$ \ $displaystyle \$$text$ {$VAR}_{\text{res}}=$$SS_$${\text{res}/n}$ ${\displaystyle {\text{및<img alt="{displaystyle {text{VAR}}\_{text{res}}=SS\_{text{res}}/n}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/9e9528c427112a8c0c4c526aaade3e0eb8a5fae1" style="vertical-align: -0.838ex; width:18.286ex; height:2.843ex;">}}_{}}$ ${\displaystyle {\text{VAR}}_{}}$ tot ${\displaystyle {}_{}}$ ${\displaystyle {}_{}tot}$ /$$n {\$displaystyle {\$text})$VAR}_{\text{tot}}=$$SS_{\text{tot}}/n}$는 추정된 잔차와 종속 변수의 표본 분산으로, 오차 및 종속 변수의 모집단 분산에 대한 편향된 추정치로 볼 수 있습니다.${\displaystyle {\text{이러한}}_{}}$ 추정치는 VAR res ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{\text{res}}_{}}$/ (${\displaystyle n}$ -${\displaystyle p}$ $)\display$ style$\text{$$VAR}_{\text{res}}=$$SS_{\text{res}/(n-p)}$ ${\displaystyle {\text{및<img alt="{displaystyle {text{VAR}}\_{text{res}}=SS\_{text{res}}/(n-p)}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/011273b9c02016870aa56c83003f47c0fa5be825" style="vertical-align: -0.838ex; width:24.105ex; height:2.843ex;">}}_{}}$ ${\displaystyle {\text{VAR}}_{}}$ 토트 ${\displaystyle {}_{}}$ ${\displaystyle {\text{토트}}_{}}$ ${\displaystyle {}_{}}$(${displaystyle {\text}$$VAR}_{\text{tot}}=$$SS_{\text{tot}}/(n-1$

오차 및 종속 변수의 모집단 분산에 대해 편향되지 않은 추정기를 사용함에도 불구하고, 수정된² R은 모집단^{2 [16]}R의 편향되지 않은 추정기가 아니며, 이는 오차 및 종속 변수의 모집단 분산을 추정하는 대신 사용하여 발생합니다.잉그램 올킨과 존 W. 프랫은 올킨-프랫 추정기로 알려진 모집단^{2 [17]}R에 대한 최소 분산 비편향 추정기를 도출했다.R을² 조정하기 위한 다양한 접근방식을 비교한 결과, 대부분의 상황에서 (Ezekiel) 보정² R보다 Olkin-Pratt 추정기의 대략적인 버전 또는 정확한 Olkin-Pratt 추정기를^[18] 선호해야 한다는 결론을 내렸다.

부분결정계수

부분 결정 계수는 축소 모형에서는 설명할 수 없는 변동의 비율로 정의할 수 있지만 완전 ^[19][20][21]모형에서 지정된 예측 변수에 의해 설명될 수 있습니다.이 계수는 하나 이상의 추가 예측 변수가 더 완전히 지정된 회귀 모형에서 유용한지 여부를 파악하는 데 사용됩니다.

부분² R에 대한 계산은 두 모형을 추정하고 해당 모형에 대한 분산 분석 표를 생성한 후 비교적 간단합니다.부분² R의 계산은 다음과 같습니다.

${\displaystyle {SS_{\text{res, reduced}}-SS_{\text{res, full}}{SS_{\text{res, reduced}}}},$

이는 일반적인 결정 계수와 유사하다.

${\displaystyle {SS_{\text{tot}}-SS_{\text{res}}}{SS_{\text{tot}}}}.}$

R의 일반화 및 분해²

위와 같이 조정된 $R{\displaystyle {}^{}}$ $(\$ R$^{2})$ 기준$$ 및 F-test와 같은 모델 선택 휴리스틱스를 통해 ${\displaystyle {R\mathrm{}}^{}}$2(\$displaystyle R^{$2})의 총량이 모델에 새로운 회귀체를 추가해야 하는지 여부를 판단한다.이미 포함된 다른 회귀 분석기와 상관관계가 높은 모델에 회귀 분석기를 추가하면 새 회귀 분석기가 관련되더라도 총 ${\displaystyle {R\mathrm{}}^{}}$ 2$(\$ R$^{2})$는 거의 증가하지 않습니다.그 결과, 위에서 언급한 휴리스틱스는 교차 상관관계가 ^[22]높을 때 관련된 퇴행자를 무시한다.

또는 일반화된 $버전$의 ${\displaystyle {R\mathrm{}}^{}}$ 2$(\$ R$^{2})$를 분해하여 ^[22]가설에서 벗어나는 관련성을 정량화할 수 있다.Hoornweg(2018)에서$$ 알 수 있듯이, 베이지안 선형 회귀, 능선 회귀 및 ($적응형)$라쏘와 같은 여러 수축 추정치는 제한되지 않은 OLS 솔루션에서 가상 값을 향해 매개변수를 점차 축소할 때 $2$의 분해를 이용한다.먼저 선형 회귀 모형을 다음과 같이 정의해 보겠습니다.

$(\displaystyle y=X\beta +\varepsilon )$

$행렬{\displaystyle }$ X$(\displaystyle$ X$)$는 Z-점수로 표준화되었으며 $열{\displaystyle }$벡터 y(\$displaystyle$ y$)$는 0의 평균을 가지도록 중심화되어 있다고 가정합니다.열 $벡터{\displaystyle {}_{}}$ ${\displaystyle {\beta \mathrm{}}_{}}$ 0$(\$ _${0})$은 귀무 가설의 회귀 파라미터를 참조하고 열 $벡터{\displaystyle }$ b$(\displaystyle$ b$)$는 추정 파라미터를 나타냅니다.그 후, 다음과 같이 정의할 수 있습니다.

${\displaystyle R^{2}=1-{(y-Xb)'(y-Xb)}{(y-X\beta_{0}(y-X\beta_{0})}}.}$

$({$ R$^{2}})$가 75%이면 ${\displaystyle {\beta \mathrm{}}_{}}$ 0$({$ _${0})$ 값이$$ $아닌{\displaystyle {}_{}}$ 데이터에 $최적화$된 b$({displaystyle$ b$})$ 솔루션을$$ 사용할 경우 표본 내 정확도가 75% 향상됨을 의미합니다.${\displaystyle {\beta \mathrm{}}_{}}$ 0$(\$ _${0})$이 0의 벡터인 $특별$한 경우 기존 ${\displaystyle {R\mathrm{}}^{}}$ 2$(\$ R$^{2})$를 다시 얻습니다.

가설에서 벗어난 $(\$ R$^{2})$에 $대한{\displaystyle {}^{}}$ 개별 효과는 R ${\$ {\$displaystyle$ R$^{\otimes}('$$R-outer{\displaystyle {}^{}}$')로 계산할 수 있다.$이{\displaystyle }$ p$\displaystyle$p $x$ p$\displaystyle$p 행렬은$$ 다음과 같습니다.

${\displaystyle R^{\otimes}=(X'{\tilde {y}}_{0})'(X')^{-1}({\tilde {y}_{0})'({\tilde {y}_{0})^{-1})$

$여기$서 y${\displaystyle {\stackrel{}{}}_{}}$~ ${\displaystyle 0_{\mathrm{}}}$ ${\displaystyle {}_{}y}$ - ${\displaystyle {}_{}}$ ${\displaystyle {\beta \mathrm{}}_{}}$0 { $displaystyle${$tilde${$y} _$ { 0 } =$$y - X \ $beta$_ { $0$}$$。R ${\$ { \ $display style$ R^ { \ $text$${$}$$} $の$ of of$$up R 2 （ \ $display$ $style$R^$${ $\}$ ） 。회귀자가 ${\displaystyle {상관관계}^{}}$가 $없고{\displaystyle {}_{}}$ ${\displaystyle {\beta \mathrm{}}_{}}$0 {$$$displaystyle$ \ $beta$_ { $0$$$}인$$ 경우 R ${\$ \ $display style$ r^ { $text$ { times }의 j$$} }의 대각 요소는 ${\displaystyle {\text{정확히}}^{}}$ 합계가 $됩니다{\displaystyle {}^{}}$.암시는 x $({$와 y$({displaystyle$y$\})$ $사이$의 $({$ r$^{2})$ 값에$$ 대응합니다.$xi$$($)와 x j({$displaystyle$ x_$$${$$j})$가 상관되어 $있는{\displaystyle {}_{}^{}}$ 경우 $({$ r_i}^{i$}^{i}^{})$의 비용이 증가할 수 있습니다.${\displaystyle R_{}^{}}$ ${\displaystyle j_{}^{}}$ ${\$ { $display style$ R _ { $jj$}^{ \ $otimes$}$$$asasease{\displaystyle {}_{}^{}}$ 。그 결과 R ${\$ { \ $display style$ R^ { \ $otimes$}}의 대각선 요소는 0보다 작을 수 있으며 예외적인 경우에는 1보다 클 수 있습니다.이러한 불확실성에 대처하기 위해 여러 수축 추정기에서 R ${\displaystyle {\{\backslash }^{}}$ ${\$ R$^{\otimes$}}의 대각 원소에 대한 가중 평균을 암묵적으로 취하여 가설 ^[22]값으로부터의 이탈의 관련성을 정량화한다.예를 보려면 래소를 클릭하십시오.

로지스틱 회귀 분석의² R

일반적으로 최대우도로 적합되는 로지스틱 회귀 분석의 경우 여러 가지 유사-R을² 선택할 수 있습니다.

하나는 원래 Cox & ^[23]Snell이 제안하고 Magee가 ^[24]독립적으로 제안한 일반화² R이다.

${\displaystyle R^{2}=1-\left({\mathcal {L}}(0)\over {\mathcal {L}}({\widehat {theta }}}})\right)^{2/n}$

${\displaystyle \mathrm{여기}}$서${\displaystyle }$L ( 0${\displaystyle }$)$${{$displaystyle {L}}$ (${\displaystyle 0\stackrel{}{}}$$)$은 절편만 있는 모델의 $우도$이고${\displaystyle ,}$ L ( ${\displaystyle \stackrel{}{^}}$^ ) {{\$displaystyle {\mathcal {L}}({\widehat$ {theta$$}}}}}}}}는$$ 추정된 모델의 우도이며, n은 표본 크기입니다.다음과 같이 쉽게 고쳐 쓸 수 있습니다.

${\displaystyle R^{2}=1-e^{\frac {2}{n}}(\ln\mathcal {L}}(0))-\ln({\mathcal {L}({\widehat {theta }}}})= 1-e^{-D/n}}}}$

여기서 D는 우도비 검정의 검정 통계량입니다.

Nagelkerke는^[25] 다음과 같은 속성을 가지고 있다고 지적했습니다.

1. 둘 다 계산할 수 있는 경우 이는 고전적인 결정 계수와 일치한다.
2. 그 값은 모델의 최대우도 추정에 의해 최대화된다.
3. 점근적으로 표본 크기와 독립적이다.
4. 해석은 모형에 의해 설명되는 변동의 비율입니다.
5. 값은 0과 1 사이이며, 0은 모델이 어떠한 변동을 설명하지 않음을 나타내고 1은 관측된 변동을 완벽하게 설명함을 나타냅니다.
6. 유닛은 없습니다.

그러나, 나는({\displaystyle{{나는\mathcal}}({\widehat{\theta}})물류 모델의 경우에는}1보다 클 수 없는 R2사이에 0과 R최대 2=1−(L(0)x2/n{\displaystyle R_{\max}({\mathcal{L}}(0))^{2/n}}:따라서, Nagelkerke는 가능 규모를 정의하는 것이 제안된다.dR²/^[26]R로서의²²_max R.

잔차 표준과의 비교

때때로 잔차의 노름은 적합도를 나타내는 데 사용됩니다.이 항은 잔차 제곱합계의 제곱근으로 계산됩니다.

${\displaystyle {\text{res}}}=syslogrt {SS_{\text{res}}}=\e\.}$

R과 잔차의 규범 모두² 상대적인 장점이 있습니다.최소 제곱 분석의² 경우 R은 0과 1 사이에서 변화하며, 숫자가 클수록 적합치가 우수하고 1이 완벽함을 나타냅니다.잔차의 노름은 0에서 무한대까지 다양하며, 작은 숫자는 더 나은 적합치를 나타내며 0은 완벽한 적합치를 나타냅니다.R의² 장점과 단점 중 하나는 ${\displaystyle {}_{}}$\$displaystyle SS_{\text{$tot$$}} $용어$가 값을 정규화하는 것입니다.y_i 값에 상수를 모두 곱하면 잔차의 노름도 해당 상수로 바뀌지만² R은 동일하게 유지됩니다.기본적으로 데이터 집합에 적합한 선형 최소 제곱의 경우:

x	1	2	3	4	5
y	1.9	3.7	5.8	8.0	9.6

R² = 0.998 및 잔차 규범 = 0.302입니다.

모든 y 값에 1000을 곱하면(예: SI 접두사 변경) R은² 동일하게 유지되지만 잔차의 규범은 302입니다.

적합에 대한 또 다른 단일 모수 지시자는 잔차의 RMSE 또는 잔차의 표준 편차입니다.이 값은 위의 예제에서 적합치가 허용되지 않은 ^[27]절편과 선형인 경우 0.135가 됩니다.

역사

결정계수의 생성은 유전학자 Sewall Wright에 의해 이루어졌으며 ^[28]1921년에 처음 출판되었다.

「 」를 참조해 주세요.

• 안스콤베 4중주
• 알 수 없는 분산 비율
• 적합도
• Nash-Sutcliffe 모델 효율성 계수(수문학적 응용 프로그램)
• Pearson 곱-모멘트 상관 계수
• 비례적 손실 감소
• 회귀 모형 검증
• 루트 평균 제곱 편차
• 단계적 회귀 분석

메모들

추가 정보

• Gujarati, Damodar N.; Porter, Dawn C. (2009). Basic Econometrics (Fifth ed.). New York: McGraw-Hill/Irwin. pp. 73–78. ISBN 978-0-07-337577-9.
• Hughes, Ann; Grawoig, Dennis (1971). Statistics: A Foundation for Analysis. Reading: Addison-Wesley. pp. 344–348. ISBN 0-201-03021-7.
• Kmenta, Jan (1986). Elements of Econometrics (Second ed.). New York: Macmillan. pp. 240–243. ISBN 978-0-02-365070-3.
• Lewis-Beck, Michael S.; Skalaban, Andrew (1990). "The R-Squared: Some Straight Talk". Political Analysis. 2: 153–171. doi:10.1093/pan/2.1.153. JSTOR 23317769.
• Chicco, Davide; Warrens, Matthijs J.; Jurman, Giuseppe (2021). "The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation". PeerJ Computer Science. 7 (e623): e623. doi:10.7717/peerj-cs.623. PMC 8279135. PMID 34307865.