대표성 휴리스틱

대표성 휴리스틱은 불확실성 상황에서 사건의 확률을 판단할 때 사용된다.^[1] 심리학자 아모스 트베르스키와 다니엘 카네만이 1970년대 초 "[사건](i)이 부모 인구와 본질적 특성이 유사한 정도이며, (ii)는 그것이 생성되는 과정의 두드러진 특징을 반영한다"고 제안한 휴리스틱스(판단이나 의사결정을 지배하는 단순한 규칙)의 하나이다."^[1]휴리스틱스는 "일반적으로 우리가 가야 할 곳, 그리고 빠르게, 그러나 때때로 우리를 진로를 벗어나게 하는 데 드는 비용으로 우리를 이끌어주는 판결의 지름길"^[2]이라고 묘사된다. 휴리스틱스는 의사 결정 시 노력 감소와 단순화를 사용하기 때문에 유용하다.^[3]

사람들이 판단을 하기 위해 대표성에 의존할 때, 어떤 것이 더 대표적이라는 사실이 실제로 그것을 더 가능성 있게 만들지 않기 때문에 그들은 잘못 판단하기 쉽다.^[4] 대표성 휴리스틱은 단순히 대상의 유사성을 평가하고 범주 프로토타입에 기초하여 그것들을 구성하는 것으로 설명된다(예를 들어, 유사성과 유사하며 원인과 효과는 서로 닮아야 한다).^[2] 이 휴리스틱은 쉬운 계산이기 때문에 사용된다.^[4] 문제는 사람들이 사건의 가능성을 정확하게 예측하는 능력을 과대평가한다는 것이다.^[5] 따라서 관련 기준 비율과 기타 인지 편견을 무시하는 결과를 초래할 수 있다.^[6][7]

대표성 결정요인

대표성 휴리스틱은 의사결정에 특정 요소가 있을 때 더 많이 사용된다.

유사성

새로운 자극/이벤트의 대표성을 판단할 때, 사람들은 보통 자극/이벤트와 표준/과정 사이의 유사성의 정도에 주목한다.^[1] 또한 그러한 특징들이 두드러지는 것도 중요하다.^[1] Nilsson, Juslin 및 Olsson(2008)은 이것이 기억의 예시 계정(구체적인 범주의 예는 메모리에 저장됨)의 영향을 받는다는 것을 발견했고, 따라서 자주 마주칠 뿐 아니라 범주와 매우 유사한 경우 새로운 인스턴스들을 대표자로 분류했다.^[8] 유사성의 몇 가지 예는 대표성 휴리스틱 문헌에 설명되어 있다. 이 연구는 의학적 신념에 초점을 맞추었다. ^[2] 사람들은 종종 의학적인 증상이 그들의 원인이나 치료법과 비슷해야 한다고 믿는다. 예를 들어, 사람들은 박테리아가 사실 궤양을 유발할 때, 대표성 휴리스틱 때문에, 스트레스에 의해 궤양이 발생한다고 오랫동안 믿어왔다.^[2] 비슷한 생각의 선에서, 어떤 대안적인 의학적인 믿음에서 환자들은 그들의 의학적 장애에 해당하는 장기 고기를 먹도록 장려되었다. 대표성 휴리스틱의 사용은 지방이 많은 음식을 먹는 것이 사람을 뚱뚱하게 만든다는 믿음과 같은 훨씬 더 단순한 믿음에서 볼 수 있다.^[2] 예를 들어, 진단에서 유사성을 판단할 때 의사들도 대표성 휴리스틱에 의해 좌우될 수 있다.^[9] 그 연구자는 임상의사들이 환자가 그 장애를 가진 정형 또는 원형 환자와 얼마나 유사한지를 판단하여 대표성 경험적 휴리스틱을 진단하는데 사용한다는 것을 발견했다.^[9]

무작위성

불규칙성과 국소 대표성은 무작위 판단에 영향을 미친다. 논리적인 순서가 없는 것으로 보이는 것들은 무작위성을 대표하는 것으로 간주되어 발생하기 쉽다. 예를 들어, 일련의 동전 던지기로서의 THTH는 순서가 너무 좋기 때문에 무작위로 생성된 동전 던지기의 대표적인 것으로 간주되지 않는다.^[1]

지역 대표성은 사람들이 소수의 법칙에 의존하는 가정이다. 작은 표본은 큰 표본과 동일한 정도로 자신의 모집단을 나타내는 것으로 인식된다(Tversky & Kahneman 1971) ^[1] 무작위로 분포된 것으로 보이는 작은 표본은 지역 대표성을 가정했을 때 모집단이 무작위로 분포한다는 믿음을 강화시킬 것이다. 반대로 분포가 왜곡된 작은 표본은 이러한 믿음을 약화시킬 것이다. ^[1] 만약 동전 던지기가 여러 번 반복되고 결과의 대다수가 "앞면"으로 구성된다면, 국지적인 대표성을 가정하면 관찰자는 동전이 "앞면"^[1]에 편향되어 있다고 믿게 될 것이다.

트베르스키와 카네만의 고전 연구

톰 W.

1973년에 행해진 한 연구에서,^[10] 카네만과 트베르스키는 그들의 참가자들을 세 그룹으로 나누었다.

• "오늘 미국의 1학년 대학원생들을 모두 고려하라"는 지시를 받은 '기본급 그룹'이다. 다음의 9개 전문분야에 현재 등록되어 있는 학생의 비율에 대한 최선의 추측을 적어주십시오." ^[10] 주어진 9개 분야는 경영학, 컴퓨터공학, 공학, 인문학 및 교육, 법률, 도서관학, 의학, 체육 및 생명과학, 사회과학 및 사회사업이었다. ^[10]
• 성격 스케치를 받은 '비슷한 그룹'들. "톰 W.는 진정한 창의력은 부족하지만 지능은 높다. 그는 질서와 명료함, 그리고 모든 세부 사항이 적절한 장소를 찾는 깔끔하고 정돈된 시스템에 대한 필요성을 가지고 있다. 그의 글은 다소 둔하고 기계적이며, 때로는 다소 진부한 말장난과 공상과학영화의 번뜩임으로 활기를 띠기도 한다. 그는 역량에 대한 강한 추진력을 가지고 있다. 그는 다른 사람들에게 거의 공감을 느끼지 못하는 것 같고 다른 사람들과 교류하는 것을 즐기지 않는 것 같다. 자기 중심적인 그는 그럼에도 불구하고 깊은 도덕적 감각을 지니고 있다." ^[10] 이 그룹의 참가자들은 Tom W.가 각 영역의 프로토타입 대학원생과 얼마나 유사한지 기준으로 파트 1에 열거된 9개 영역의 순위를 매겨달라는 요청을 받았다. ^[10]
• '예언군'은 2에서 설명한 성격 스케치를 받았지만 '톰 W.의 선행 성격 스케치는 심리학자가 톰의 고등학교 3학년 때 프로젝트적인 테스트를 바탕으로 작성했다'는 정보도 제공받았다. 톰 W.는 현재 대학원생이다. 톰 W.가 현재 이 분야 각각 대학원생일 가능성에 따라 다음의 9개 대학원 전문분야의 순위를 매겨주십시오."

우도의 판단은 추정된 기준 비율보다 유사성의 판단에 훨씬 더 가까웠다. 이 연구 결과는 사람들이 상대적인 기준금리 정보에 근거하는 것이 아니라 (비슷한) 어떤 것이 얼마나 대표적인가에 근거하여 예측을 한다는 저자들의 예측을 뒷받침했다. ^[10] 예를 들어, 95% 이상의 참여자들은 톰이 교육이나 인문학보다 컴퓨터 과학을 공부할 가능성이 높다고 답했는데, 이때 교육이나 인문학에 대한 기본율 추정치가 컴퓨터 과학에 비해 훨씬 높았다. ^[10]

택시 문제

Tversky와 Kahneman이 수행한 또 다른 연구에서는 다음과 같은 문제가 주어졌다.^[4]

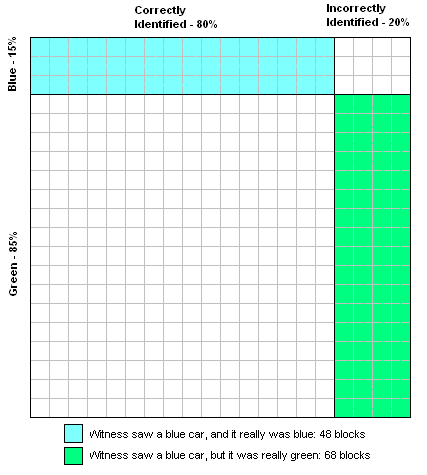
밤에 택시 한 대가 뺑소니 사고를 당했다. 두 개의 택시 회사인 그린과 블루가 이 도시에서 운영된다. 시내 택시 중 85%가 그린이고 15%는 블루다. ^[4]

목격자는 그 택시가 블루라고 확인했다. 법원은 사고 당일 밤 존재했던 것과 같은 상황에서 증인의 신빙성을 시험한 결과 증인이 두 가지 색깔 각각을 80%씩 정확하게 식별하고 20%는 불합격했다고 결론 내렸다. ^[4]

사고와 관련된 택시가 이 목격자가 블루라고 밝힌 것을 그린이 아닌 블루였을 가능성은 얼마나 될까? ^[4]

대부분의 과목은 50% 이상의 확률을 보였으며, 80% 이상의 정답이 나온 과목도 있었다. 베이스의 정리를 이용해 찾은 정답은 다음과 같은 추정치보다 낮다.^[4]

• 증인이 파란색 택시를 정확히 식별할 확률은 12%(15% 곱하기 80%)이다.
• 목격자의 17%(85% 곱하기 20%)가 녹색 택시를 파란색으로 잘못 식별할 가능성이 있다.
• 따라서 증인이 택시를 파란색으로 식별할 확률은 29%(12% + 17%)이다.
• 이는 파란색으로 식별된 택시가 실제로 파란색일 확률을 41%(12%로 나눈 29%)로 만든다.

대표성은 도박꾼의 오류, 회귀의 오류, 연결의 오류와 유사한 효과에서 인용된다. ^[4]

대표성 휴리스틱에 기인하는 편견

기준금리무시 및 기준금리 오류

대표성 휴리스틱의 사용은 베이즈 정리 위반으로 이어질 가능성이 높다. 베이즈 정리에는 다음과 같이 명시되어 있다.^[11]

${\displaystyle P(H D)={\frac {P(D H)\,P(H)}{P(D)}}.}$

그러나 대표성에 의한 판단은 가설과 데이터의 유사성만을 고려할 뿐이므로 역확률은 다음과 같다.^[11]

$[\displaystyle P(H D)=P(D H)}$

알 수 있듯이 이 방정식에서는 기준금리 P(H)가 무시되어 기준금리 오류로 이어진다. 기본률은 현상의 기본 발생률이다. 기준금리 오류는 사람들이 확률 문제를 해결할 때 사건의 기준금리를 고려하지 않는 방법을 설명한다.^[12] 이것은 특정한 성격 특성을 가진 사람들의 기본 비율과 주어진 성격 특성을 가진 사람이 또 다른 성격을 가질 확률을 모두 판단하도록 한 도스, 미렐스, 골드, 도나휴(1993)에 의해 명백하게 테스트되었다. ^[11] 예를 들어 100명 중 얼마나 많은 사람이 '나는 양심적인 사람이다'라는 질문에 진실하게 대답하는지, 한 사람이 이 질문에 진실하게 대답하는 것을 볼 때, 얼마나 많은 사람들이 다른 성격 질문에 진실하게 대답할 것인지에 대한 질문을 받았다. 그들은 참가자들이 역 확률을 동일시한다는 것을 발견했다($예{\displaystyle }$: P${\displaystyle }$(${\displaystyle c}$ ${\displaystyle o}$ s ${\displaystyle i}$ ${\displaystyle e}$ ${\displaystyle i}$ ${\displaystyle o}$ ${\displaystyle o}$ ${\displaystyle o}$ ${\displaystyle o}$ ${\displaystyle o}$ o ${\displaystyle u}$ ${\displaystyle o}$ o o o ${\displaystyle o}$ ${\displaystyle o}$ i c${\displaystyle }$)$$= P${\displaystyle }$(${\displaystyle n}$ ${\displaystyle e}$ ${\displaystyle u}$ ${\displaystyle o}$ ${\displaystyle o}$ o ${\displaystyle o}$ o ${\displaystyle u}$ )${\displaystyle }${\$displaystyle$ P ($양심 신경증)=$$P(신체적 양심)}$는 같지 않은 것이 분명할 때에도$($두 질문은 서로 바로 뒤에 답하였다. ^[11]

의학적 예는 액셀슨에 의해 설명된다.^[12] 의사가 99%의 정확도를 가진 검사를 수행하면, 당신은 그 질병에 대해 양성반응을 보인다고 가정해당. 그러나 발병률은 1만분의 1이다. 건강한 사람들의 인구가 그 질병보다 훨씬 많기 때문에 당신이 그 병에 걸릴 확률은 1%이다. ^[12] 이 통계는 종종 사람들을 놀라게 하는데, 기준금리 오류 때문이다. 많은 사람들이 확률을 판단할 때 기본적인 발생률을 고려하지 않기 때문이다. ^[12] Maya Bar-Hillel(1980)의 연구에 따르면, 정보의 관련성이 인지된 것은 기본율 방치에 필수적이라고 한다. 즉 기본율은 다른 정보와 동등하게 관련성이 있는 것으로 보이는 경우에만 판단에 포함된다.^[13]

일부 연구는 이러한 판단 휴리스틱스가 어떻게 발전하는지에 대한 이해가 부족했기 때문에 어린이들의 기준금리 무시에 대해 탐구해왔다.^[14][15] 그러한 연구의 저자들은 사회적 판단과 다른 판단 사이에 차이가 있다면, 그리고 아이들이 대표성 경험 경험적 경험적 경험적 접근법을 사용하지 않을 때 기준금리를 사용하는지 여부를 이해하기를 원했다. ^[15] 저자들은 대표성 휴리스틱을 전략으로서 사용하는 것이 일찍부터 시작되고 일관된다는 것을 발견했다. 저자들은 또 아이들이 처음에는 사회적 판단을 하기 위해 특유한 전략을 쓰고, 나이가 들수록 기준금리를 더 많이 사용하지만, 사회적 영역에서 대표성 휴리스틱의 사용도 나이가 들수록 증가한다는 사실을 발견했다.^[15] 저자들은 조사 대상 아동들 가운데 기준금리가 사회적 판단보다 사물에 대한 판단에 더 쉽게 사용된다는 사실을 발견했다.^[15] 그 연구가 시행된 후, 데이빗슨(1995)은 어린이들의 정형화와 관련된 어린이들의 대표성 휴리스틱과 접속사 오류를 탐구하는 데 관심이 있었다.^[14] 이전의 연구와 일관되게, 아이들은 문제가 비철형 정보를 포함하거나 아이들이 나이가 들었을 때 기본 비율에서 벗어난 문제에 대한 그들의 반응을 바탕으로 했다. 아이들이 접속사 오류를 범한다는 증거도 있었다. 마지막으로, 학생들은 나이가 들면서 정형화된 문제들에 대해 대표성 휴리스틱을 사용했고, 그래서 고정관념과 일치하는 판단을 했다.^[14] 심지어 아이들도 대표성 휴리스틱을 사용하고, 접속사 오류를 범하며, 기준금리를 무시한다는 증거가 있다. ^[14]

연구 결과 기준금리 사용이나 방치는 문제를 제시하는 방식에 영향을 받을 수 있다고 제안해 대표성 휴리스틱이 '일반적인, 모든 목적 휴리스틱스'가 아니라 기여 요인이 많을 수 있음을 상기시킨다.^[16] 제시된 정보가 인과적이지 않을 때 기준금리는 더 자주 무시될 수 있다.^[17] 관련 개별 정보가 있는 경우 기본 요율을 덜 사용한다.^[18] 단체들은 개인보다 기준금리를 더 소홀히 하는 것으로 밝혀졌다.^[19] 기본 요율의 사용은 상황에 따라 다르다.^[20] 일부 저자들은 새로운 모델이 필요하다고 제안하는 등 기준금리 사용에 대한 연구는 일관성이 없었다.^[21]

접속사 오류

한 무리의 대학생들에게 린다에 대한 설명이 제공되었는데, 이는 적극적인 페미니스트를 대표하는 것으로 모델링되었다. 그리고 나서 참가자들은 그녀가 페미니스트일 확률, 은행원이 될 확률, 은행원과 페미니스트 둘 다일 확률을 평가해 달라는 요청을 받았다. ^[22] 확률 이론은 은행 창구자와 페미니스트 둘 다일 확률은 페미니스트나 은행 창구 둘 중 하나일 확률보다 작거나 같아야 한다고 지시한다.^[22] 연결은 그 구성원의 하나보다 더 개연성이 있을 수 없다. 그러나 참가자들은 접속사(은행원, 페미니스트)가 은행원 혼자일 가능성보다 더 높다고 판단했다.^[22] 일부 연구에서는 접속사 오류가 부분적으로 "확률성"^[23][24]의 모호한 표현이나 의미 해석과 같은 미묘한 언어적 요인에 기인할 수 있다고 제안한다. 저자들은 논리 사용과 언어 사용 모두 오류와 관련이 있을 수 있으며, 좀 더 충분히 조사되어야 한다고 주장한다.^[24]

분리 오류

확률론에서 두 사건의 분리는 적어도 두 사건 중 하나와 개별적으로 동일할 가능성이 있다. ^[22] 예를 들어, 물리학과나 생물학과가 될 확률은 적어도 물리학과가 될 가능성은 더 많지는 않지만 최소한 물리학과가 될 가능성은 있다. 그러나, 성격 설명(데이터)이 생물학 전공에 비해 물리학 전공(예: 포켓 프로텍터)을 매우 대표하는 것처럼 보일 때, 사람들은 이 사람이 자연과학 전공(물리학의 상위 집합)보다 물리학 전공자가 될 가능성이 더 높다고 판단한다. ^[22]

대표성 휴리스틱이 분리 오류를 일으킬 수 있다는 증거는 Bar-Hillel과 Neter(1993)에서 나온다.^[25] 이들은 통계전공(예: 지능이 높은 사람, 수학경시대회)을 대표하는 사람을 사회과학전공(통계전공)보다 통계전공(통계전공)일 가능성이 높다고 판단하지만 인문전공(수)보다는 히브리어전공일 가능성이 높다고 생각하지 않는다는 사실을 발견했다.히브리어의 쓰임새). ^[22] 따라서, 어떤 범주를 매우 대표하는 것으로 보이는 경우에만 그 범주가 그 범주의 초범위 범주보다 더 가능성이 높다고 판단된다. 이러한 잘못된 평가들은 확률에 대한 내기에서 실제 돈을 잃는 상황에서도 남아 있었다. ^[22]

시료크기에 대한 불감증

피험자가 표본의 특정 모수의 확률을 추정할 때도 대표성 경험적 접근법을 사용한다. 모수가 모집단을 높게 나타내는 경우 모수에 높은 확률을 부여하는 경우가 많다. 이 추정 과정은 일반적으로 표본 크기의 영향을 무시한다.

Tversky와 Kahneman이 제안한 개념은 이러한 편향의 예를 제공한다.

그 예는 규모가 다른 두 병원의 경우다. 약 45명의 아기들이 대형병원에서 태어나고 15명의 아기들이 작은병원에서 태어난다. 전체 출생아 중 절반(50%)이 남자아이다. 그러나 이 비율은 하루에서 이틀로 바뀐다. 각 병원은 1년 동안 태어난 아기의 60%가 남자아이인 날을 기록하였다. 제기되는 질문은 다음과 같다. 어느 병원이 그런 날들을 더 많이 기록했다고 생각하십니까? ^[26]

• 대형 병원(21)
• 작은 병원(21)
• 거의 동일(즉, 서로 5% 이내) (53)

괄호 안에 표시된 값은 각 답을 선택하는 학생의 수입니다. ^[26]

결과에 따르면 응답자의 절반 이상이 오답(제3의 선택)을 선택한 것으로 나타났다. 이는 응답자들이 표본 크기의 효과를 무시하기 때문이다. 응답자들은 세 번째 선택권을 가장 많이 선택했는데, 그 이유는 동일한 통계가 크고 작은 병원 모두를 나타내기 때문이다. ^[26] 통계 이론에 따르면, 표본 크기가 작으면 큰 표본에 비해 통계적 매개변수가 상당히 편차가 있을 수 있다. ^[26] 따라서 대형병원은 명목값인 50%에 근접할 확률이 더 높을 것이다.

아래 기사에서 이러한 편향에 대해 자세히 알아보십시오.

우연에 대한 오해와 도박꾼의 오류

회귀오류

참고 항목

• 경험적 휴리스틱
• 속성 대체
• 가용성 경험적 접근성
• 판단과 의사결정의 편향 목록
• 연장방치

참조

카네만과 트베르스키의 작품

• Tversky, Amos; Kahneman, Daniel (1971). "Belief in the law of small numbers". Psychological Bulletin. 76 (2): 105–110. CiteSeerX 10.1.1.592.3838. doi:10.1037/h0031322.
• Kahneman, Daniel; Tversky, Amos (1972). "Subjective probability: A judgment of representativeness" (PDF). Cognitive Psychology. 3 (3): 430–454. doi:10.1016/0010-0285(72)90016-3.
• Kahneman, Daniel; Tversky, Amos (1973). "On the psychology of prediction". Psychological Review. 80 (4): 237–251. doi:10.1037/h0034747.
• Tversky, Amos; Kahneman, Daniel (1974). "Judgment under Uncertainty: Heuristics and Biases" (PDF). Science. 185 (4157): 1124–1131. Bibcode:1974Sci...185.1124T. doi:10.1126/science.185.4157.1124. PMID 17835457. S2CID 143452957.
• Tversky, Amos; Kahneman, Daniel (1982). "Evidential Impact of Base Rates". In Kahneman, Daniel; Slovic, Paul; Tversky, Amos (eds.). Judgment Under Uncertainty: Heuristics and Biases. Science. 185. Cambridge University Press. pp. 1124–31. doi:10.1126/science.185.4157.1124. ISBN 978-0-521-28414-1. PMID 17835457. S2CID 143452957.
• Tversky, Amos; Kahneman, Daniel (1983). "Extensional versus intuitive reasoning: The conjunction fallacy in probability judgment". Psychological Review. 90 (4): 293–315. doi:10.1037/0033-295X.90.4.293.

일반참조

• Baron, Jonathan (2000). Thinking and Deciding (3rd ed.). Cambridge University Press. ISBN 978-0-521-65972-7.
• Plous, Scott (1993). The Psychology of Judgment and Decision Making. McGraw-Hill Education. ISBN 978-0-07-050477-6.

외부 링크

• 대표성 경험적 휴리스틱에 대한 파워포인트 프레젠테이션(고전 실험의 프레젠테이션에 대한 추가 링크 포함)