베이즈 정리

시리즈의 일부
베이지안 통계
사후 = 가능성 × 사전 ÷ 증거
배경
베이지안 추론 베이지안 확률 베이즈 정리 번스타인-본 미제스 정리 코히어런스 콕스 정리 크롬웰의 법칙 무관심의 원리 최대 엔트로피의 원리
모형건물
약한 이전... 강력한 선행 켤레전수 선형회귀 익스피리언스 베이즈 계층 모델
후방 근사
마르코프 사슬 몬테카를로 라플라스 근사 통합 중첩 라플라스 근사 변분추론 베이지안 근사 계산
추정기
베이지안 추정기 신뢰구간 최대 사후 추정
증거 근사
증거 하한 중첩 샘플링
모델평가
베이즈 팩터 모델 평균화 사후예측
수학포털
v t

확률 이론과 통계학에서, 토마스 베이즈의 이름을 딴 베이즈 정리(대체로 베이즈의 법칙 또는 베이즈의 법칙)는 사건과 관련이 있을 수 있는 조건에 대한 사전 지식을 기반으로 사건의 확률을 설명합니다.^[1] 예를 들어, 건강 문제가 발생할 위험이 나이가 들수록 증가하는 것으로 알려진 경우, 베이즈 정리는 알려진 연령의 개인에 대한 위험을 단순히 개인이 전체 인구의 전형적이라고 가정하는 것이 아니라 연령에 따라 조건을 지정함으로써 더 정확하게 평가할 수 있도록 합니다.

베이즈 정리의 많은 응용 중 하나는 통계적 추론에 대한 특별한 접근법인 베이지안 추론입니다. 적용 시 정리에 포함된 확률은 서로 다른 확률 해석을 할 수 있습니다. 베이지안 확률 해석을 사용하여 이 정리는 확률로 표현되는 믿음의 정도가 관련 증거의 가용성을 설명하기 위해 합리적으로 변화해야 하는 방법을 표현합니다. 베이지안 추론은 베이지안 통계학의 기본이며, 한 권위자는 "피타고라스의 정리가 기하학에 어떤 것인지에 대한 확률 이론"으로 간주합니다.^[2]

역사

베이즈 정리는 통계학자이자 철학자이기도 한 토마스 베이즈 목사(/be ɪ레스/)의 이름을 따서 지어졌습니다. 베이즈는 조건부 확률을 사용하여 증거를 사용하여 미지의 모수에 대한 한계를 계산하는 알고리즘(그의 명제 9)을 제공했습니다. 그의 작품은 1763년에 '기회론의 문제해결을 위한 에세이'로 출판되었습니다. Bayes는 (현대 용어로) 이항 분포의 확률 모수에 대한 분포를 계산하는 방법을 연구했습니다. 베이즈가 죽자 그의 가족은 그의 논문을 친구인 목사, 철학자, 수학자 리처드 프라이스에게 옮겼습니다.

리차드 프라이스는 2년에 걸쳐 출판되지 않은 원고를 상당히 편집한 후 1763년 12월 23일 왕립학회에서 그것을 큰 소리로 읽은 친구에게 보냈습니다.^[3] 프라이스는 철학적 거래에 등장하는 베이즈의 대표작 '우연의 이론에서 문제를 해결하기 위한 에세이'(1763)를^[4] 편집해 베이즈의 정리를 담고 있습니다.^[5] 프라이스는 베이즈 통계학의 철학적 기초 중 일부를 제공하는 논문에 대한 소개를 작성하고 베이즈가 제공하는 두 가지 해결책 중 하나를 선택했습니다. 1765년, 프라이스는 베이즈의 유산에 대한 그의 업적을 인정받아 왕립학회의 회원으로 선출되었습니다.^[6][7] 4월 27일, 그의 친구 벤자민 프랭클린에게 보낸 편지가 왕립 학회에서 낭독되었고, 이후 출판되었습니다. 프라이스는 이 작업을 인구와 컴퓨터 '수명-연금'에 적용합니다.^[8]

1774년에 베이즈와 독립적으로 피에르-시몽 라플라스, 그리고 이후 1812년에 그의 테오리 분석 기법 des probabilités에서 조건부 확률을 사용하여, 증거가 주어졌을 때, 사전 확률로부터 업데이트된 사후 확률의 관계를 공식화했습니다. 그는 1774년에 베이즈의 연구 결과를 재현하고 확장시켰는데, 그는 분명히 베이즈의 연구 결과를 알지 못했습니다.^{[note 1][9]} 확률에 대한 베이지안 해석은 주로 Laplace에 의해 개발되었습니다.^[10]

약 200년 후, 해롤드 제프리스 경은 베이즈의 알고리즘과 라플라스의 공식을 공리적 기반 위에 올려놓았고, 1973년 책에서 베이즈의 정리는 "피타고라스의 정리가 기하학에 어떤 것인지에 대한 확률론에 관한 것"^[2]이라고 썼습니다.

스티븐 스티글러는 베이즈의 정리를 베이즈보다 얼마 전에 영국의 맹인 수학자 니콜라스 손더슨이 발견했다고 베이즈의 주장을 사용했지만,^[11][12] 그 해석은 논쟁의 여지가 있습니다.^[13] Martyn^[14] Hooper와 Sharon^[15] McGrayne은 Richard Price의 기여가 상당하다고 주장했습니다.

현대적 기준으로 보면 베이즈-프라이스 룰을 참조해야 합니다. 프라이스는 베이즈의 작품을 발견하고, 그 중요성을 인식하고, 이를 수정하고, 기사에 기고하고, 그것의 용도를 찾았습니다. 베이즈의 이름만을 사용하는 현대적 관습은 불공평하지만 너무 확고해서 다른 것들은 거의 말이 되지 않습니다.^[15]

정리문

베이즈 정리는 수학적으로 다음과 같은 방정식으로 표현됩니다.^[16]

여기서 $A$ ${\displaystyle A}$ 및 $B$ ${\displaystyle$ B$}$는 이벤트이고 $P{\displaystyle (B)}$ ≠ 0${\displaystyle$P(B)\n$eq$ 0$\}.$

• ${\displaystyle P(AB)}$ ${\displaystyle$ P$(A\vert B)}$는 조건부 확률입니다. $B{\displaystyle }$ ${\displaystyle B}$가 참일 때 이벤트 $A{\displaystyle }$ ${\displaystyle$ A$}$가 발생할 확률입니다. $B{\displaystyle }$ ${\displaystyle B}$가 주어진$$ A ${\displaystyle$ A$}$의 사후 확률이라고도 합니다$.$
• ${\displaystyle P(BA)}$ ${\displaystyle$ P$(B\vert$ A$)}$도 조건부 확률입니다$$. $A{\displaystyle }$ ${\displaystyle$ $A$$}$가 참일 때 $이벤트{\displaystyle }$ B ${\displaystyle$ B$}$가 발생할 확률입니다. $P{\displaystyle (BA)}$ = ${\displaystyle L(AB)}$ ${\displaystyle$ P$(B$\vert A) = L(A\vert B)}이기 때문에 $고정$된$$B {\$displaystyle$ B$}$가 주어졌을 때 A ${\displaystyle A}$일 가능성도 해석할 수 있습니다.
• ${\displaystyle P(A)}$ ${\displaystyle P(A)}$ 및 P${\displaystyle (B)}$ ${\displaystyle$ P$(B)}$는 주어진 조건 없이 $각각{\displaystyle }$$$ A ${\displaystyle$ A$}$ 및 $B$ ${\displaystyle B}$를 관찰할 확률이며, 이를 사전 확률 및 한계 확률이라고 합니다.

증명

이벤트용

베이즈 정리는 조건부 확률의 정의로부터 유도될 수 있습니다.

${\displaystyle P(A\vert B)={\frac {P(A\cap B)}{P(B)}},{\text{ if }}P(B)\neq 0,}$

여기서 $($ ∩ B) ${\displaystyle P($A\cap B)}는 A와 B가 모두 참일 확률입니다. 유사하게,

${\displaystyle P(B\vert A)={\frac {P(A\cap B)}{P(A)}},{\text{ if }}P(A)\neq 0.}$

$A$∩ B) {\$displaystyle P(A$\cap B)}를 풀고 P$(A$ B) ${\displaystyle$P($A\$vert B)}에 위${\displaystyle }식을$ 대입하면 베이즈 정리가 나옵니다.

${\displaystyle P(A\vert B)={\frac {P(B\vert A)P(A)}{P(B)}},{\text{ if }}P(B)\neq 0.}$

연속형 랜덤 변수의 경우

두 개의 연속형 랜덤 변수 X와 Y에 대해 베이즈 정리는 조건부 밀도의 정의로부터 유사하게 유도될 수 있습니다.

${\displaystyle f_{X\vert Y=y}(x)={\frac {f_{X,Y}(x,y)}{f_{Y}(y)}}}$

${\displaystyle f_{Y\vert X=x}(y)={\frac {f_{X,Y}(x,y)}{f_{X}(x)}}}$

그러므로,

${\displaystyle f_{X\vert Y=y}(x)={\frac {f_{Y\vert X=x}(y)f_{X}(x)}{f_{Y}(y)}}.}$

일반적인 경우

Let ${\displaystyle P_{Y}^{x}}$ be the conditional distribution of ${\displaystyle Y}$ given ${\displaystyle X=x}$ and let ${\displaystyle P_{X}}$ be the distribution of ${\displaystyle X}$. 그러면 결합 분포는 ${\displaystyle {PX,}_{}}$ ${\displaystyle Y_{}}$(${\displaystyle d}$ x${\displaystyle ,}$ ${\displaystyle \mathrm{dy}}$) = ${\displaystyle {}_{}^{}}$ x${\displaystyle {}_{}^{}}$(${\displaystyle \mathrm{dy}}$ $)$ PX (d x ) {\displaystyle P_{X,Y} (dx,dy) =$P_{Y}^{x}(dy)$$P_{X}(dx$ $Y$ = ${\displaystyle y}$ ${\displaystyle$ Y = y$}$가 주어지면 $X$ ${\displaystyle X}$ 의 조건부 분포 $P$ ${\displaystyle {}_{}^{}}$ y ${\displaystyle P_{X}^{y}}$는 다음에 의해 결정됩니다.

라돈-니코딤 정리의 결과는 필요한 조건부 기대의 존재와 유일성입니다. 이것은 1933년 콜모고로프가 그의 유명한 책에서 공식화한 것입니다. 콜모고로프는 서문에서 "나는 ..., 특히 조건부 확률과 조건부 기대 이론에 주의를 환기하고 싶다"고 적음으로써 조건부 확률의 중요성을 강조합니다.^[17] 베이즈 정리는 이전 분포로부터 사후 분포를 결정합니다. 베이즈 정리는 실수선의 균일 분포와 같은 부적절한 사전 분포를 포함하도록 일반화될 수 있습니다.^[18] 현대의 마르코프 체인 몬테카를로 방법은 부적절한 사전이 있는 경우를 포함하여 베이즈 정리의 중요성을 높였습니다.^[19]

예

레크리에이션 수학

베이즈의 규칙과 계산 조건부 확률은 세 죄수 문제, 몬티 홀 문제, 두 차일드 문제, 두 봉투 문제와 같은 여러 인기 퍼즐에 대한 해결 방법을 제공합니다.

약물검사

누군가가 대마초를 사용했는지 여부에 대한 특정 테스트는 90% 민감도이며, 이는 실제 양성 비율(TPR) = 0.90을 의미합니다. 따라서 대마초 사용자에게 90%의 진정한 긍정적인 결과(의약품 사용에 대한 정확한 식별)로 이어집니다.

또한 검정은 80% 특이적이며, 이는 참 음성 비율(TNR) = 0.80을 의미합니다. 따라서 이 테스트는 비사용자의 경우 비사용자의 경우 80%를 정확하게 식별하지만 비사용자의 경우 20%의 거짓 양성 또는 거짓 양성 비율(FPR) = 0.20을 생성합니다.

대마초를 사용하는 사람의 5%를 의미하는 0.05의 유병률을 가정할 때, 양성 반응을 보이는 무작위 사람이 실제로 대마초 사용자일 확률은 얼마입니까?

검사의 양성 예측값(PPV)은 양성 반응을 보인 사람 중 실제로 양성 반응을 보인 사람의 비율로, 표본에서 다음과 같이 계산할 수 있습니다.

PPV = True positive / 양성 판정

민감도, 특이도, 유병률이 알려진 경우 베이즈 정리를 이용하여 PPV를 계산할 수 있습니다. $($ ${\displaystyle \text{Positive})}$ {\$displaystyle P({\text{$User$}}\vert{\text${Positive$}}$는 "양성 반응을 보인 사람이 대마초 사용자일 확률"을$$ 의미하며, 이는 PPV가 의미하는 바입니다. 다음과 같이 쓸 수 있습니다.

${\displaystyle {begin{aligned}P({\text{User}}\vert{text{Positive}}&={\frac{P({\text{Positive}}\vert{text{User}})P({\text{User}})}{P({\text{Positive}})})\\&={\frac {P({\text{Positive}}\vert{\text{User}})P({\text{User}})}{P({\text{Positive}}\vert{\text{User}})P({\text{User}})+P({\text{Positive}}\vert{\text{Non-User}})P({\text{Non-user}})}}\\[8pt]&={\frac {0.90\times 0.05}{0.90\times 0.05+0.20\times 0.95}}={\frac {0.045}{0.045+0.19}}\approx 19\%\end{aligned}}}$

$P{\displaystyle (\text{Positive})}$ = ${\displaystyle P(\text{Positive}}$ $)$ P($사용자)$ + P(Positive Non-User) P(비사용자) {\displaystyle P({\text{Positive}}) = P({\text{Positive}\vert{text{User}})라는 사실$P({\text{User}})+P({\text{Positive}}\vert{\text{Non-User}})$$P({\text{Non-user}})}$는 총 확률 법칙을 직접 적용한 것입니다$$. 이 경우 사용자가 양성 반응을 보일 확률은 사용자가 양성 반응을 보일 확률, 사용자가 아닌 사용자가 양성 반응을 보일 확률, 사용자가 아닌 사용자가 양성 반응을 보일 확률의 곱이라고 말합니다. 이것은 분류 사용자와 비사용자가 한 집합, 즉 약물 테스트를 받는 사람들의 집합의 파티션을 형성하기 때문에 사실입니다. 이는 조건부 확률의 정의와 결합되어 위와 같은 문장이 됩니다.

즉, 어떤 사람이 양성 반응을 보이더라도 대마초 사용자일 확률은 19%에 불과합니다. 이 그룹에서 사용자는 5%에 불과하고, 대부분의 양성은 나머지 95%에서 나오는 거짓 양성이기 때문입니다.

1,000명이 검사를 받은 경우:

• 950명은 미사용자이며 190명은 위양성(0.20 × 950)
• 그중 50명은 사용자이고 45명은 진정한 긍정을 제시합니다(0.90 × 50).

따라서 1,000명의 사람들은 235개의 양성 반응을 얻으며, 그 중 45개만이 약 19%의 실제 약물 사용자입니다. 주파수 상자를 사용한 그림은 그림 1을 참조하십시오. 참양성의 분홍색 영역이 거짓양성의 파란색 영역에 비해 얼마나 작은지 주목하십시오.

민감성 또는 특이성

특이성의 중요성은 민감도를 100%로 높이고 특이도를 80%로 유지해도 대마초 사용자가 양성 반응을 보일 확률은 19%에서 21%로 증가하는 데 불과하지만 민감도를 90%로 유지하고 특이도를 95%로 증가시키면 49%로 증가한다는 것을 보여줌으로써 알 수 있습니다.

시험 실제.	포지티브	아니요.		총
사용자	45	5		50
비사용자	190	760		950
총	235	765	1000
민감도 90%, 특이도 80%, PPV=45/235 ≈ 19%

시험 실제.	포지티브	아니요.		총
사용자	50	0		50
비사용자	190	760		950
총	240	760	1000
민감도 100%, 특이도 80%, PPV=50/240 ≈ 21%

시험 실제.	포지티브	아니요.		총
사용자	45	5		50
비사용자	47	903		950
총	92	908	1000
민감도 90%, 특이도 95%, PPV=45/92 ≈ 49%

암발생률

췌장암 환자의 100%가 특정 증상을 가지고 있다고 해도, 같은 증상을 가지고 있을 때 이 사람이 췌장암에 걸릴 확률이 100%인 것은 아닙니다. 전 세계적으로 10/999명의 건강한 사람들이 동일한 증상을 보이는 가운데 췌장암 발생률이 10만분의 1이라고 가정하면, 그 증상을 감안할 때 췌장암에 걸릴 확률은 9.1%에 불과하고, 나머지 90.9%는 '거짓 양성'(즉, 거짓으로 암에 걸렸다고 함)일 수 있습니다. 여기서 '양성'은 다음과 같이 혼동되는 용어입니다. 시험은 나쁜 소식을 전합니다).

다음 표는 발생률을 기준으로 인구 10만 명당 해당 숫자를 제시합니다.

증상 암	네.	아니요.		총
네.	1	0		1
아니요.	10	99989		99999
총	11	99989	100000

그런 다음 증상이 있을 때 암에 걸릴 확률을 계산하는 데 사용할 수 있습니다.

${\displaystyle {begin{aligned}P({\text{Cancer}} {\text{Symptoms})&={\frac{P({\text{Symptoms}} {\text{Cancer})P({\text{Cancer}})}{P({\text{증상}})})\\&={\frac {P({\text{증상}} {\text{Cancer}})P({\text{Cancer}})}{P({\text{Symptoms}}{\text{Cancer})P({\text{Cancer}})+P({\text{증상}} {\text{Non-Cancer}}P({\text{Non-Cancer}}}}\[8pt]&={\frac {1\times 0.00001}{1\times 0.00001+(10/99999)\times 0.999}}={\frac {1}{11}\approx 9.1\%\end{aligned}}}$

불량품율

조건. 기계.	결함이 있는	무결점		총
A	10	190		200
B	9	291		300
C	5	495		500
총	24	976	1000

공장은 생산량의 20%, 30%, 50%를 차지하는 A, B, C 세 가지 기계를 사용하여 제품을 생산합니다. A 기계에서 생산된 제품 중 5%가 불량이며, 마찬가지로 B 기계의 제품 중 3%와 C 기계의 제품 중 1%가 불량입니다. 임의로 선택한 품목이 불량품이라면, 기계 C에서 생산되었을 확률은 얼마입니까?

다시 한 번 가상의 경우에 조건을 적용하면 공식을 사용하지 않고도 답에 도달할 수 있습니다. 예를 들어, 공장에서 1,000개의 품목을 생산할 경우, 200개는 기계 A, 300개는 기계 B, 500개는 기계 C에서 생산됩니다. A 기계는 5% × 200 = 10개의 불량품, B 기계는 3% × 300 = 9개, C 기계는 1% × 500 = 5개로 총 24개를 생산하게 됩니다. 따라서 임의로 선택된 불량품이 기계 C에서 생성되었을 가능성은 5/24(~20.83%)입니다.

이 문제는 베이즈 정리를 사용하여 해결할 수도 있습니다. 임의로 선택된 항목이 i 기계에 의해 만들어졌다는 사건을 X라고 합니다(i = A, B, C). 임의로 선택한 항목에 결점이 있는 경우를 Y라고 합니다. 그런 다음 다음 정보를 제공받습니다.

${\displaystyle P(X_{A})=0.2,\quad P(X_{B})=0.3,\quad P(X_{C})=0.5.}$

제품이 첫 번째 기계에 의해 만들어진 경우 불량일 확률은 0.05, 즉 P(Y X) = 0.05입니다. 전반적으로, 우리는

${\displaystyle P(Y X_{A})=0.05,\quad P(Y X_{B})=0.03,\quad P(Y X_{C})=0.01.}$

원래 질문에 답하기 위해 먼저 P(Y)를 구합니다. 다음과 같은 방법으로 수행할 수 있습니다.

${\displaystyle P(Y)=\sum _{i}P(YX_{i})P(X_{i})=(0.05)(0.2)+(0.03)(0.3)+(0.01)(0.5)=0.024.}$

따라서 전체 출력의 2.4%가 불량입니다.

우리는 Y가 발생했다고 주어졌고, 우리는 X의_C 조건부 확률을 계산하려고 합니다. 베이즈 정리에 의하면

${\displaystyle P(X_{C} Y)={\frac {P(Y X_{C})P(X_{C})}{P(Y)}}={\frac {0.01\cdot 0.50}{0.024}}={\frac {5}{24}}}$

제품이 불량인 것을 감안하면 C 기계로 만들 확률은 5/24 입니다. 기계 C는 전체 생산량의 절반을 생산하지만 불량품의 훨씬 적은 부분을 생산합니다. 따라서 선택한 항목에 결함이 있다는 지식을 통해 이전 확률 P(X) = 1/2을 더 작은 사후 확률 P(XY) = 5/24로 대체할 수 있습니다.

해석

베이즈 법칙의 해석은 조건에 따른 확률의 해석에 달려 있습니다. 두 가지 주요 해석은 아래에 설명되어 있습니다. 그림 2는 기하학적 시각화를 보여줍니다.

베이지안 해석

베이지안(또는 인식론적) 해석에서 확률은 "믿음의 정도"를 측정합니다. 베이즈 정리는 증거를 설명하기 전과 후의 명제에 대한 믿음의 정도를 연결합니다. 예를 들어, 동전이 꼬리보다 앞면이 두 배 더 떨어질 가능성이 50% 확실하다고 가정해 보겠습니다. 만약 동전이 여러 번 뒤집히고 관찰된 결과가 나온다면, 그 믿음의 정도는 아마도 상승하거나 하락할 것이지만, 결과에 따라 심지어 그대로 유지될 수도 있습니다. 명제 A와 증거 B에 대하여,

• P(A), 즉 선행은 A에 대한 초기 믿음의 정도입니다.
• 후방인 P(A B)는 B가 진실이라는 뉴스를 접목한 후의 믿음의 정도입니다.
• 몫의 몫 P(BA)/P(B)는 B가 A에 제공하는 지원을 나타냅니다.

확률의 베이지안 해석 하에서 베이즈 정리의 적용에 대한 자세한 내용은 베이지안 추론을 참조하십시오.

빈도주의적 해석

빈도주의적 해석에서 확률은 "결과의 비율"을 측정합니다. 예를 들어, 실험이 여러 번 수행되었다고 가정합니다. P(A)는 속성이 A인 결과의 비율(이전)이고, P(B)는 속성이 B인 결과의 비율입니다. P(BA)는 속성이 A인 결과의 비율이고, P(AB)는 속성이 A인 결과의 비율(이전)입니다.

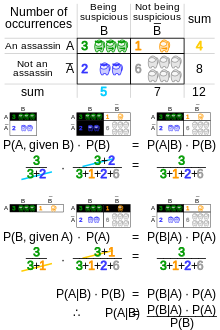
베이즈 정리의 역할은 그림 3과 같은 트리 다이어그램으로 가장 잘 시각화됩니다. 두 다이어그램은 동일한 결과를 A와 B로 반대 순서로 분할하여 역확률을 구합니다. 베이즈 정리는 서로 다른 분할을 연결합니다.

예

곤충학자는 등에 있는 무늬 때문에 딱정벌레의 희귀한 아종일 수도 있는 것을 발견합니다. 희귀 아종의 전체 98%가 패턴을 가지고 있으므로 P(Pattern Rare) = 98%입니다. 일반적인 아종의 5%만이 패턴을 가지고 있습니다. 이 희귀한 아종은 전체 개체수의 0.1%입니다. 딱정벌레가 희귀한 패턴을 가질 가능성은 얼마나 될까요? P(희귀한 패턴)란 무엇입니까?

베이즈 정리의 확장된 형태로부터 (어떤 딱정벌레도 드물거나 흔하기 때문에),

${\displaystyle {begin{aligned}P({\text{Rare}}\vert{text{Pattern})&={\frac{P({\text{Pattern}}\vert{\text{Rare})P({\text{Rare}})}}{P({\text{Pattern})}}\[8pt]&={\frac{P({\text{Pattern}}\vert{\text{Rare}})P({\text{Rare}})}{P({\text{Pattern}}\vert{\text{Rare}})P({\text{Rare}})+P({\text{Pattern}}\vert{\text{Common}})P({\text{Common}})}}\\[8pt]&={\frac {0.98\times 0.001}{0.98\times 0.001+0.05\times 0.999}}\\[8pt]&\approx 1.9\%\end{aligned}}}$

양식

이벤트

심플폼

사건 A와 사건 B의 경우, P(B)가 ≠ 0인 경우,

${\displaystyle P(A B)={\frac {P(B A)P(A)}{P(B)}}.}$

예를 들어 베이지안 추론과 같은 많은 응용 분야에서 이벤트 B는 논의에서 고정되며, 다양한 가능한 이벤트 A에 대한 믿음에 대한 영향을 고려하고자 합니다. 이러한 상황에서 마지막 표현식의 분모인 주어진 증거 B의 확률은 고정되어 있습니다. 우리가 변화시키고자 하는 것은 A입니다. 베이즈 정리는 사후 확률이 분자에 비례한다는 것을 보여주기 때문에 마지막 방정식은 다음과 같습니다.

${\displaystyle P(A B)\propto P(A)\cdot P(B A).}$

즉, 후방은 가능성의 이전 시간에 비례합니다.^[20]

사건 A₁, A₂, ...가 상호 배타적이고 완전한 경우, 즉 둘 중 하나는 발생하지만 둘은 함께 발생할 수 없는 경우, 우리는 그들의 확률이 1을 더해야 한다는 사실을 사용하여 비례 상수를 결정할 수 있습니다. 예를 들어, 주어진 이벤트 A에 대해 이벤트 A 자체와 그 보완 ¬A는 배타적이고 완전합니다. 비례 상수를 c로 나타냄

${\displaystyle P(A B)=c\cdot P(A)\cdot P(B A){\text{ and }}P(\neg A B)=c\cdot P(\neg A)\cdot P(B \n예 A)}$

이 두 공식을 더하면 다음과 같은 결과를 얻을 수 있습니다.

${\displaystyle 1=c\cdot (P(B A)\cdot P(A)+P(B \neg A)\cdot P(\neg A)),}$

아니면

${\displaystyle c={\frac {1}{P(B A)\cdot P(A)+P(B \neg A)\cdot P(\neg A)}}={\frac {1}{P(B)}}.}$

대체양식

분할표

배경 명제	B	¬B (B가 아님)		총
A	P(BA)·P(A) = P(AB)·P(B)	P(¬BA)·P(A) = P(A ¬B)·P(¬B)		P(A)
¬A (A가 아님)	P(B ¬A)·P(¬A) = P(¬AB)·P(B)	P(¬B ¬A)·P(¬A) = P(¬A ¬B)·P(¬B)		P(¬A) = 1−P(A)
총	P(B)	P(¬B) = 1-P(B)	1

두 개의 경쟁 문장 또는 가설에 대한 베이즈 정리의 또 다른 형태는 다음과 같습니다.

${\displaystyle P(A B)={\frac {P(B A)P(A)}{P(B A)P(A)+P(B \neg A)P(\n)egA)}}}(으)}(으).$

인식론적 해석의 경우:

명제 A와 증거 또는 배경 B에 대하여,^[21]

• ${\displaystyle P(A)}$ ${\displaystyle$ P$(A)}$는 사전 확률, 즉 A에 대한 초기 믿음의 정도입니다.
• $(¬$$eg A)}$는 A가 거짓이라는 ${\displaystyle \mathrm{not-A}}$에 대한 대응하는 초기 믿음의 정도이며, 여기서 $P{\displaystyle (}$$¬$ ${\displaystyle A}$) $=$ ${\displaystyle 1}$ - P$(A$) {\$displaystyle$ P(\n$)$$eg A)=1-P(A)}$
• ${\displaystyle P(BA)}$ ${\displaystyle$ P$(BA)}$는 명제 A가 참일 때 B에 대한 믿음의 정도인 조건부 확률 또는 가능성입니다.
• $¬$$eg A)}$는 명제 A가 거짓인 경우 B에 대한 믿음의 정도인 조건부 확률 또는 가능성입니다.
• ${\displaystyle P(AB)}$ ${\displaystyle P(AB)}$는 사후 확률로 B를 고려한 후 A의 확률입니다.

확장양식

종종 표본 공간의 일부 파티션 {A_j}에 대해 이벤트 공간은 P(A_j) 및 P(BA_j)로 표시됩니다. 그러면 총 확률의 법칙을 사용하여 P(B)를 계산하는 것이 유용합니다.

${\displaystyle P(B)=\sum _{j}P(B\cap A_{j}),}$

또는 (조건부 확률에 대한 곱셈 규칙 사용),^[22]

${\displaystyle P(B)={\sum _{j}P(B A_{j})P(A_{j})},}$

${\displaystyle \rightarrow P(A_{i} B)={\frac {P(BA_{i})P(A_{i})}{\sum \limits _{j}P(B A_{j})P(A_{j})}}\cdot }$

A가 이진 변수인 특수한 경우:

${\displaystyle P(A B)={\frac {P(B A)P(A)}{P(B A)P(A)+P(B \neg A)P(\n)eg A)}\cdot }$

랜덤 변수

두 개의 랜덤 변수 X와 Y에 의해 생성된 표본 공간 ω를 생각해 보십시오. 원칙적으로 베이즈 정리는 이벤트 A = {X = x}와 B = {Y = y}에 적용됩니다.

${\displaystyle P(X{=}x Y{=}y)={\frac {P(Y{=}y X{=}x)P(X{=}x)}{P(Y{=}y)}}}$

그러나 두 변수 중 하나가 유한 확률 밀도를 갖는 점에서는 항이 0이 됩니다. 유용성을 유지하기 위해서는 베이즈 정리가 관련 밀도의 관점에서 공식화되어야 합니다(도함수 참조).

심플폼

X가 연속이고 Y가 이산이면,

${\displaystyle f_{X Y{=}y}(x)={\frac {P(Y{=}y X{=}x)f_{X}(x)}{P(Y{=}y)}}}$

여기서 각 $f{\displaystyle }$ ${\displaystyle f}$는 밀도 함수입니다.

X가 이산이고 Y가 연속이면,

${\displaystyle P(X{=}x Y{=}y)={\frac {f_{Y X{=}x}(y)P(X{=}x)}{f_{Y}(y)}}.}$

X와 Y가 모두 연속적이라면,

${\displaystyle f_{X Y{=}y}(x)={\frac {f_{Y X{=}x}(y)f_{X}(x)}{f_{Y}(y)}}.}$

확장양식

연속 이벤트 공간은 종종 분자 용어로 개념화됩니다. 그러면 총 확률의 법칙을 사용하여 분모를 제거하는 것이 유용합니다. f_Y(y)의 경우, 이것은 적분이 됩니다.

${\displaystyle f_{Y}(y)=\int _{-\infty }^{\infty }f_{Y X=\xi }(y)f_{X}(\xi )\,d\xi .}$

베이즈의 오즈형태의 규칙

오즈 형태의 베이즈 정리는 다음과 같습니다.

${\displaystyle O(A_{1}:A_{2}\vert B)=O(A_{1}:A_{2})\cdot \Lambda (A_{1}:A_{2}\vert B)}$

어디에

${\displaystyle \Lambda(A_{1:A_{2}\vert B)={\frac {P(B\vert A_{1})}{P(B\vert A_{2})}}}$

베이즈 계수 또는 우도비라고 합니다. 두 사건 사이의 확률은 단순히 두 사건의 확률의 비율입니다. 따라서

${\displaystyle O(A_{1}:A_{2})={\frac {P(A_{1})}{P(A_{2})}},}$

${\displaystyle O(A_{1}:A_{2}\vert B)={\frac {P(A_{1}\vert B)}{P(A_{2}\vert B)}},}$

따라서, 사후 확률은 베이즈 요인의 사전 확률의 곱, 즉 사후 확률은 사전 확률의 곱에 비례한다고 규칙은 말합니다.

$A$ ${\displaystyle 1_{}}$ = ${\displaystyle A}$ ${\$$displaystyle$ $A_{$1} = A} 및 A 2 = A {\displaystyle$A_${2} =\n이라는 특수한 경우$eg A$ $O{\displaystyle (A)}$ $=$ ${\displaystyle O(A:}$ $¬$ A) $=$ P(A) / $(1$- P(A)) ${\displaystyle O$(A) $=$ O(A:\n)라고 적습니다.$eg$A)$=$P(A)/($1-P(A)}$이며$$베이즈 인수와 조건부 승산에 대해서도 유사한 약어를 사용합니다. $A{\displaystyle }$ ${\displaystyle A}$의 확률은 정의상 A ${\displaystyle$ A$}$에 대한 확률과 A에 대한 확률입니다$.$ 그러면 베이즈의 규칙은 축약된 형태로 작성될 수 있습니다.

${\displaystyle O(A\vert B)=O(A)\cdot \Lambda(A\vert B),}$

또는, 다시 $,$ A {\$displaystyle$ A$}$의 후방 승산은 A ${\displaystyle$ A$}$의 $사전{\displaystyle }$ 승산과 정보 $B{\displaystyle }$ ${\displaystyle B}$가 주어진 A ${\displaystyle A}$의 우도비의 곱과$$ 같습니다$$$.$ 간단히 말해서, 후방 승산은 사전 승산 시간 우도비와 같습니다.

예를 들어, 의료 검사의 민감도가 90%이고 특이도가 91%인 경우 양성 베이즈 인자는${\displaystyle {}_{}}$λ + = P(참 ${\displaystyle 양성)}$/ P(거짓${\displaystyle }$양성) = 90% / (100% - 91%) = 10 ${\$displaystyle \Lambda _{+} =$$P({\text{$True Positive}}/P({\text{False Positive$})$=90\%/(100\$winth91\%)$=10$ 자, 이 질병의 유병률이 9.09%이고, 그 확률을 사전 확률로 본다면 사전 확률은 1:10 정도가 됩니다. 따라서 양성 판정을 받은 후 실제로 질병에 걸릴 확률의 사후 확률은 1:1이 되는데, 이는 질병에 걸릴 확률의 사후 확률이 50%라는 것을 의미합니다. 연속 검사에서 두 번째 검사를 수행한 결과 양성으로 판명되면 실제 질병에 걸릴 확률은 10:1이 되며, 이는 약 90.91%의 사후 확률을 의미합니다. 음성 베이즈 인자는 91%/(100%-90%)=9.1로 계산할 수 있으므로 두 번째 검정에서 음성으로 판명되면 실제 질병에 걸릴 확률은 1:9.1이며, 이는 약 9.9%의 사후 확률을 의미합니다.

위의 예는 더 확실한 숫자로도 이해할 수 있습니다: 검사를 받는 환자가 1000명의 집단에서 왔다고 가정하면, 그 중 91명이 실제로 질병을 가지고 있습니다(유병률 9.1%). 이 1000명이 모두 건강진단을 받게 되면 해당 질환자 중 82명이 진양성 결과(감도 90.1%), 해당 질환자 중 9명이 위음성 결과(위음성률 9.9%), 해당 질환자가 없는 827명이 진음성 결과(특이도 91.0%), 그리고 이 질환이 없는 사람 중 82명은 위양성 결과(false 양성률 9.0%)를 얻게 됩니다. 검사를 받기 전에 환자가 질병에 걸릴 확률은 91:909입니다. 양성 결과를 받은 후 환자가 질병에 걸릴 확률은

${\displaystyle {\frac {91}{909}}\times {\frac {90}.1\%}{9.0\%}}={\frac {91\times 90.1\%}{909\times 9.0\%}}=1:1}$

1000명의 그룹에 82개의 참양성과 82개의 거짓양성이 있다는 사실과 일치합니다.

다른 수학적 틀과의 대응

명제논리학

${\displaystyle P(}$¬ BA) ${\displaystyle \mathrm{사용}}$= ${\displaystyle 1}$ -${\displaystyle }$P$(BA$) {\$displaystyle$ P(\n$)$$예 B\vert$A)$=1-P$(${\displaystyle B}$$\vert$A)} 두 번$,$ 베이즈 정리를 사용하여 $P{\displaystyle (}$$¬$ $B$$¬$ A)를 표현할 수도 $있습니다$. ${\displaystyle$ P(\n)$예: B\vert \n$$eg A)}$는 P${\displaystyle (AB)}${\$displaystyle$P($A\vert$ B$)}$의 관점에서$$ 그리고 부정이 없습니다.

$)$$예: B\vert \n$$eg A)=1-\left(1-P(A\vert B)\right){\frac {P(B)}{P(\n$$egA$

${\displaystyle P(}$¬ A) = ${\displaystyle 1}$- P($A)$ ≠ 0${\displaystyle$ P(\n)일 때$eg A)=1-P(A)\n$$eq$ 0$\}.$ 이로부터 추론을 읽을 수 있습니다.

$1$$예: B\vert \n$$eg$ A)$=$1}.

말로 표현하면: $확실히$ B$${\$displaystyle$ B$}$가 A$${\$displaystyle$A}를 의미한다면$,$ 우리는 $확실히$¬ A {\$displaystyle$ \n이라고 추론합니다.$egA}$은(는) $¬$ B ${\displaystyle$ \n을 의미합니다.$예$ B$}.$여기서 $P$(${\displaystyle \mathrm{B})}$$≠$ 0${\displaystyle$ P(B$)\$n$eq$ 0$\},$ 확실한 두 의미는 동등한 문장입니다. 확률 공식에서 조건부 $확률$ P${\displaystyle (AB)}$ ${\$$displaystyle$ $P(A\vert$ B$)}$는 ${\displaystyle 논리적}$ 의미 B ⟹ A ${\displaystyle$ B$\imples$ A}를 일반화하며, 이제 참 또는 거짓을 할당하는 것을 넘어 문에 확률 값을 할당합니다. $B$⟹ A {\$displaystyle$ B$\imples$ A}의 주장은 조건부의 확실성, 즉${\displaystyle }$P(A ${\displaystyle \mathrm{B}}$)$$= 1${\displaystyle$ P($A\$vert B)= 1}의${\displaystyle }주장$에 의해 포착됩니다. 암시의 방향과 관련하여, 베이즈의 정리는 고전 명제 논리에서 다음과 같이 표현될 수 있는 배치 법칙의 일반화를 나타냅니다.

$B ⟹$$eg A\implies \n$$eg$ B$)\}.$

이 관계에서 $A{\displaystyle }$ ${\displaystyle A}$의 위치는 반응합니다$$. ${\displaystyle B}$ ${\displaystyle$ B$}$이(가) 뒤집힙니다.

확률 미적분학의 관점에서 대응하는 공식은 베이즈 정리이며, 이전 확률/기준 비율을 포함하는 확장된 형태로 A ${\displaystyle$ $A$$}$만 포함하는 ${\displaystyle$ $a$는 다음과 같이 표현됩니다.^[23]

$a$$eg A)\,a(\n$$)$$eg$ A$)\}\}\}.$

주관적 논리

베이즈 정리는 주관적 논리에서 반전된 조건부 의견을 도출하는 특별한 경우를 나타내며, 다음과 같이 표현됩니다.

${\displaystyle(\omega_{A{\tilde {}}B}^{S},\omega_{A{\tilde {}}\lnot B}^{S})=(\omega_{B\vert A}^{S},\omega_{B\vert \lnot A}^{S}){\widetilde {\phi}}a_{A}}$

여기서$$ϕ ~ ${\displaystyle {\widetilde${\phi}}은 조건부 의견을 반전하는 연산자를 나타냅니다. 인수${\displaystyle {}_{}^{}}$ω B ${\displaystyle {AS}_{}^{}}$,$$ω B ¬ AS)${\displaystyle$(\$omega_{B\vert$A}^{$S},\omega_${B\vert \lnot A}^{S}}는$소스$ S {\$displaystyle$ ${\displaystyle S_{}}$}가 $제공$하는 이항 조건부 $의견$쌍을 의미하며$, 인수$ A {\displaystyle a_{$A}$는 $A{\displaystyle }$ ${\displaystyle A}$의 사전 확률(일명 기준 속도)을 나타냅니다$$$.$ 도함수 반전 조건부 $의견$의 쌍은${\displaystyle {\stackrel{}{}}_{}^{}}$ω${\displaystyle {}_{}^{}}$A ~ B${\displaystyle {}_{}^{}}$S,$$ω A ~ ¬ B) ${\displaystyle(\omega$_{$A{\tilde {}}^{S},\omega$_{$A$tilde {}}\lnot B}^{S}}로 표시됩니다. 조건부 오피니언$$ω AB S ${\displaystyle \omega$_{$A\vert$ B}^{S}}는 확률적${\displaystyle 조건부}$P$(AB$) ${\displaystyle$P($A$vert B)}를 일반화합니다. 소스 $S{\displaystyle }$ ${\displaystyle S}$는 확률을 할당하는 것 외에도 조건문$({\displaystyle AB)}$ ${\displaystyle (A\vert B)}$에 주관적 의견을 할당할$$ 수 있습니다$.$ 이항 주관적 의견$$ω AS ${\displaystyle \omega_{$A}^{S}}는 소스 S ${\displaystyle$S}에 의해 표현되는 인식적 불확실성의 정도를 갖는$문장$ A ${\displaystyle$ A}의 진리에 대한 믿음입니다. 모든 주관적인 의견은 해당하는 투영 $확률$ P$($ω AS) ${\displaystyle$ P$(\omega_$A}^{S})}를 가지고 있습니다. 베이즈 정리를 투영된 의견 확률에 적용하는 것은 동형화이며, 이는 베이즈 정리가 의견의 투영된 확률로 표현될 수 있음을 의미합니다.

${\displaystyle P(\omega _{A{\tilde { }}B}^{S})={\frac {P(\omega _{B\vert A}^{S})a(A)}{P(\omega _{B\vert A}^{S})a(A)+P(\omega _{B\vert \lnot A}^{S})a(\lnot A)}}.}$

따라서 주관적 베이즈 정리는 베이즈 정리의 일반화를 나타냅니다.^[24]

일반화

세 사건에 대한 베이즈 정리

세 가지^[25] 사건에 대한 베이즈 정리의 버전은 모든 확률이 조건화된$$ 세 번째 $사건{\displaystyle }$ C$${\$displaystyle$ C$}$의 추가에서 비롯됩니다.

${\displaystyle P(A\vert B\cap C)={\frac {P(B\vert A\cap C)\,P(A\vert C)}{P(B\vert C)}}$

파생

체인 규칙 사용

${\displaystyle P(A\cap B\cap C)=P(A\vert B\cap C)\,P(B\vert C)\,P(C)}$

그리고 다른 한편으로는

${\displaystyle P(A\cap B\cap C)=P(B\cap A\cap C)=P(B\vert A\cap C)\,P(A\vert C)\,P(C)}$

$원하는$ 결과는 P${\displaystyle (\mathrm{AB}}$ ∩ C) {\$displaystyle$ P($A\vert$B$\backslash$cap C)}에 대한 식을 모두 식별하고 풀이하면 얻어집니다.

유전학에서의 사용

유전학에서 베이즈 정리는 특정 유전자형을 가진 개체의 확률을 계산하는 데 사용될 수 있습니다. 많은 사람들이 유전병에 의해 영향을 받을 가능성이나 관심이 있는 열성 유전자의 보균자가 될 가능성을 근사하려고 합니다. 가족력이나 유전자 검사를 바탕으로 베이지안 분석을 수행하여 개인이 질병에 걸릴지, 자식에게 질병을 물려줄지 예측할 수 있습니다. 유전자 검사와 예측은 아이를 가질 계획이지만 특히 유전적 변이가 낮은 지역 사회에서 둘 다 질병의 매개체가 될 수 있다고 우려하는 부부들 사이에서 일반적인 관행입니다.^[26]

유전학에 대한 베이지안 분석의 첫 번째 단계는 상호 배타적인 가설을 제안하는 것입니다: 특정 대립유전자에 대해 개체는 보균자이거나 그렇지 않습니다. 다음으로 Prior Probability(가족력이나 멘델의 상속에 근거한 예측 등의 정보를 고려한 각 가설의 가능성), 조건부 확률(어떤 결과의), 합동 확률(처음 두 개의 곱), 그리고 사후 확률(각 가설에 대한 합동 확률을 두 합동 확률의 합으로 나누어 계산한 가중 곱). 이런 유형의 분석은 순전히 어떤 질환의 가족력에 근거하거나 유전자 검사와 함께 수행될 수 있습니다.^{[citation needed]}

혈통을 사용하여 확률 계산

가설	가설 1: 환자는 보균자입니다	가설 2: 환자는 보균자가 아닙니다
사전 확률	1/2	1/2
조건부 네 자손 모두가 영향을 받지 않을 확률	(1/2) · (1/2) · (1/2) · (1/2) = 1/16	한 1개 정도
합동확률	(1/2) · (1/16) = 1/32	(1/2) · 1 = 1/2
사후 확률	(1/32) / (1/32 + 1/2) = 1/17	(1/2) / (1/32 + 1/2) = 16/17

질병이 형제자매에게는 존재하지만 부모나 네 자녀에게는 존재하지 않는다는 지식에 기초한 질병에 대한 여성 개인의 위험에 대한 베이지안 분석표의 예. 피험자의 형제와 부모의 상태만을 기준으로 할 때, 그녀는 비보균자일 가능성이 동등합니다(이러한 가능성은 사전 가설로 표시됩니다). 그러나 피험자의 4명의 아들이 모두 영향을 받지 않을 확률은 1/16(1/16)입니다.1 ⁄2·1 ⁄2·1 ⁄2·1 ⁄2) 통신사인 경우 1, 비통신사인 경우 1 정도입니다(이것이 조건부 확률입니다). 합동 확률은 이 두 예측을 함께 곱하여 조정합니다. 마지막 선(사후 확률)은 각 가설의 합동 확률을 두 합동 확률의 합으로 나누어 계산됩니다.^[27]

유전자 검사 결과 사용

부모의 유전자 검사는 부모의 알려진 질병 대립유전자의 약 90%를 검출할 수 있으며, 이는 자녀의 보균자 또는 영향을 받는 상태로 이어질 수 있습니다. 낭포성 섬유증은 7번 염색체의 qarm에 ^[28]위치한 CFTR 유전자의 상염색체 열성 돌연변이에 의해 발생하는 유전성 질환입니다.^[29]

낭포성 섬유증(CF) 가족력이 있는 여성 환자를 대상으로 한 베이지안 분석 결과, 이 방법을 사용하여 CF로 태어날 아이의 위험을 결정하는 방법을 보여줍니다.

환자는 영향을 받지 않기 때문에 야생형 대립유전자에 대해 동형접합을 하거나 이형접합을 합니다. 사전 확률을 설정하기 위해 부모 모두 질병의 영향을 받지 않았지만 둘 다 보균자일 수 있다는 지식을 기반으로 Punnet Square를 사용합니다.

어머니. 아버지.	W 야생에 대한 동형접합- type 대립유전자(비 carrier)	M 이형접합성 (CF 캐리어)
W 야생에 대한 동형접합- type 대립유전자(비 carrier)	WW	엠더블유
M 이형접합체(CF 캐리어)	엠더블유	음. (낭포성 섬유증의 영향을 받음)

환자가 영향을 받지 않는다는 점을 고려할 때 가능성은 세 가지뿐입니다. 이 세 가지 안에서 환자가 돌연변이 대립유전자를 운반하는 두 가지 시나리오가 있습니다. 따라서 사전 확률은 2 ⁄3과 1 ⁄3입니다.

다음으로 유전자 검사를 받고 낭포성 섬유화 음성 판정을 받습니다. 이 테스트는 탐지율이 90%이므로 음성 테스트의 조건부 확률은 1/10 및 1입니다. 마지막으로 관절 및 후방 확률은 이전과 같이 계산됩니다.

가설	가설 1: 환자는 보균자입니다	가설 2: 환자는 보균자가 아닙니다
사전 확률	2/3	1/3
조건부 음성 검정 확률	1/10	1
합동확률	1/15	1/3
사후 확률	1/6	5/6

환자의 남성 파트너에 대해 동일한 분석을 수행한 후(음성 테스트 결과 포함), 자녀가 영향을 받을 확률은 보균자라는 부모 각자의 사후 확률의 곱과 두 보균자가 영향을 받는 자손을 생성할 확률의 곱(1 ⁄4)과 같습니다.

다른 위험인자 식별과 병행하여 수행하는 유전자 검사

베이지안 분석은 유전자 조건의 표현형 정보를 이용하여 수행할 수 있으며, 유전자 검사와 결합하면 분석이 훨씬 더 복잡해집니다. 예를 들어, 낭포성 섬유증은 초음파를 통해 태아가 에코 발생성 장을 찾음으로써 확인할 수 있는데, 이는 스캔에서 정상보다 밝게 나타나는 장을 의미합니다. 완전히 건강한 태아에게 에코 발생 장이 존재할 수 있기 때문에 이것은 바보 같은 테스트가 아닙니다. 부모 유전자 검사는 표현형 인자가 확률 계산에 지나치게 영향을 미칠 수 있는 경우에 매우 영향력이 있습니다. 에코성 장을 가진 태아의 경우 검사를 받고 CF 보균자로 알려진 산모가 있는 경우 태아가 실제로 질병에 걸릴 확률은 매우 높습니다(0.64). 그러나 아버지가 CF에 대해 음성 판정을 받으면 사후 확률이 유의하게 떨어집니다(0.16으로).^[27]

위험인자 계산은 유전자 상담과 생식계획에 있어 강력한 도구이지만 중요한 고려 요소로만 취급할 수는 없습니다. 위와 같이 불완전한 테스트는 통신사 상태의 잘못된 높은 확률을 산출할 수 있으며, 부모가 없을 때 테스트는 재정적으로 접근이 불가능하거나 실행이 불가능할 수 있습니다.

참고 항목

• 베이지안 인식론
• 귀납확률
• 양자 베이즈주의
• 존 이오아니디스의 2005년 메타과학 에세이, 가장 많이 발표된 연구 결과가 거짓인 이유
• 정규조건확률

메모들

참고문헌

서지학

• 이 문서는 현재 공용 도메인에 있는 출판물의 텍스트를 통합합니다.

더보기

• Grunau, Hans-Christoph (24 January 2014). "Preface Issue 3/4-2013". Jahresbericht der Deutschen Mathematiker-Vereinigung. 115 (3–4): 127–128. doi:10.1365/s13291-013-0077-z.
• Gelman, A, Carlin, JB, Stern, HS 및 Rubin, DB(2003), "Bayesian Data Analysis", Second Edition, CRC Press.
• 대신 CM과 Snell, JL(1997), "확률 입문(2판)", 미국 수학 학회(무료 pdf 이용 가능)[1].
• "Bayes formula", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• McGrayne, SB (2011). The Theory That Would Not Die: How Bayes' Rule Cracked the Enigma Code, Hunted Down Russian Submarines & Emerged Triumphant from Two Centuries of Controversy. Yale University Press. ISBN 978-0-300-18822-6.
• Laplace, Pierre Simon (1986). "Memoir on the Probability of the Causes of Events". Statistical Science. 1 (3): 364–378. doi:10.1214/ss/1177013621. JSTOR 2245476.
• Lee, Peter M(2012), 베이지안 통계: 서론, 4판. 와일리. ISBN 978-1-118-33257-3.
• Puga JL, Krzywinski M, Altman N (31 March 2015). "Bayes' theorem". Nature Methods. 12 (4): 277–278. doi:10.1038/nmeth.3335. PMID 26005726.
• Rosenthal, Jeffrey S(2005), "번개에 찔렸다: 호기심 많은 확률의 세계"라고 말했습니다. 하퍼 콜린스(Granta, 2008) ISBN 9781862079960).
• Stigler, Stephen M. (August 1986). "Laplace's 1774 Memoir on Inverse Probability". Statistical Science. 1 (3): 359–363. doi:10.1214/ss/1177013620.
• Stone, JV(2013), "Bayes's Rule: A Tutorial Introduction to Bayesian Analysis", Sebtel Press, 영국
• 베이지안 지능인 추론, 통계학과 인지과학에서 베이즈 정리의 사용에 대한 소개 및 튜토리얼.
• Morris, Dan (2016), "베이즈 정리의 예"에서 처음 6장을 읽어 보십시오. 초보자를 위한 비주얼 소개" 블루 윈드밀 ISBN 978-1549761744. 문제 시나리오를 이해하고 P(B), P(A), P(BA)를 찾는 방법에 대한 간단한 튜토리얼입니다.

외부 링크

• 유튜브에서 나무를 이용한 베이즈의 시각적 설명
• 베이즈의 빈발성 해석, 유튜브에서 시각적으로 설명
• 일부 수학 단어의 초기 알려진 용도 (B). "Bayesian", "Bayes' Theorem", "Bayes Estimate/Risk/Solution", "Empirical Bayes", "Bayes Factor"의 기원을 포함합니다.
• 옥스퍼드 대학교 심리학과 학생들을 위해 고안된 확률과 베이즈 정리에 관한 지도서
• 엘리저 S의 베이즈 정리에 대한 직관적인 설명 유드코프스키
• 베이지안 임상진단모형