고무탄성

고무 탄성성은 교차 연결된 고무의 성질을 가리킨다. 고무는 원래 길이에서 최대 10배까지 늘어날 수 있고, 풀리면 원래 길이에 매우 가깝게 돌아온다. 이는 고무의 명백한 성능 저하 없이 여러 번 반복될 수 있다. 고무는 엘라스토머라고 불리는 더 큰 종류의 재료의 구성원으로, 그들의 경제적, 기술적 중요성을 과대평가하기 어렵다. 엘라스토머스는 20세기 신기술 개발에 핵심적인 역할을 했고 세계 경제에 상당한 기여를 했다.^{[citation needed]} 고무 탄성은 몇 가지 복잡한 분자 과정에 의해 생성되며 그 설명에는 고급 수학, 화학, 통계 물리학, 특히 엔트로피 개념에 대한 지식이 필요하다. 엔트로피는 분자에 저장되는 열 에너지의 척도로 생각될 수 있다. 폴리부타디엔이나 폴리이소프렌(천연고무라고도 함)과 같은 일반적인 고무들은 중합이라는 공정에 의해 생산된다. 매우 긴 분자(폴리머)는 화학 반응을 통해 짧은 분자 중추 단위를 추가함으로써 순차적으로 축적된다. 고무 중합체는 다른 많은 고무 분자와 섞이면서 3차원으로 무작위적이고 지그재그로 된 길을 따라간다. 탄성체는 황과 같은 분자를 연결하는 몇 퍼센트의 교차점이 추가되어 생성된다. 열을 가하면 교차링크 분자는 어느 지점(크로스링크)에서 두 개의 고무분자를 화학적으로 결합(본드)하는 반응을 일으킨다. 고무 분자는 너무 길기 때문에, 각각의 분자는 연속적인 분자 네트워크를 형성하는 많은 다른 고무 분자와 많은 교차 연계에 참여한다. 고무줄이 늘어나면서 일부 네트워크 체인은 직진할 수밖에 없고 이로 인해 엔트로피가 감소한다. 엔트로피의 감소는 네트워크 체인의 탄성력을 발생시킨다.

역사

15세기 후반 신대륙에서 유럽으로 유입된 데 이어 천연고무(폴리소프렌)가 대부분 매혹적인 호기심으로 여겨졌다. 그것의 가장 유용한 용도는 종이 위의 연필 자국을 문질러 지우는 능력이었고, 그래서 그것의 이름이다. 그것의 가장 독특한 특성 중 하나는 고무 샘플을 늘렸을 때 발생하는 약간의 온도 상승이다. 빠르게 수축할 수 있는 경우 동일한 양의 냉각이 관찰된다. 이 현상은 영국 물리학자 존 고우의 관심을 끌었다. 1805년 그는 이러한 특징과 온도에 따라 필요한 스트레칭 힘이 어떻게 증가했는지에 대한 몇 가지 정성적 관찰을 발표했다.^[1]

19세기 중반까지 열역학 이론이 개발되고 있었고, 이 틀 안에서 영국의 수학자 겸 물리학자인 켈빈^[2] 경은 고무 샘플을 늘이는 데 필요한 기계적 에너지의 변화는 온도 상승에 비례해야 한다는 것을 보여주었다. 나중에, 이것은 엔트로피의 변화와 연관될 것이다. 열역학과의 연관성은 1859년 영국의 물리학자 제임스 줄(James Joule)이 고무 샘플이 늘어나면서 발생하는 온도 상승에 대한 최초의 신중한 측정을 발표하면서 확고하게 정착되었다.^[3] 이 작품은 켈빈 경의 이론적 예측을 확인시켜 주었다.

미국의 발명가 찰스 굿이어는 1838년에 이르러서야 천연고무의 성질이 몇 퍼센트 황을 첨가함으로써 엄청나게 개선될 수 있다는 것을 발견했다. 짧은 유황 체인은 인접한 폴리이소프렌 분자 사이에 화학적 교차 연계를 생성했다. 교차 연결되기 전에 액상 천연고무는 매우 긴 선형 체인으로 구성되며, 수천 개의 이소프렌 등뼈 단위가 들어 있고, 머리와 꼬리가 서로 연결되어 있다. 모든 사슬은 액체를 통과하는 임의의 길을 따라가고 수천 개의 다른 근처의 사슬들과 접촉한다. 약 150C까지 가열하면 교차 링커 분자(황 또는 과산화디쿠밀 등)가 분해될 수 있으며, 그에 따른 화학 반응으로 인접 체인 사이의 화학적 결합이 생성된다. 그 결과는 3차원 분자망이다. 원래의 모든 폴리이소프렌 체인은 이러한 화학 결합(네트워크 노드)에 의해 여러 지점에서 함께 연결되어 하나의 거대한 분자를 형성한다. 고무 밴드는 라텍스 글러브처럼 하나의 분자다! 같은 체인에 있는 두 개의 교차 링크 사이의 구간은 네트워크 체인이라고 불리며 최대 수백 개의 이소프렌 단위를 포함할 수 있다. 천연고무에서는 각각의 교차연결이 그것으로부터 4개의 체인이 나오는 네트워크 노드를 생산한다. 네트워크는 엘라스토머가 아닌 사인 쿼다.

고무의 엄청난 경제적, 기술적 중요성 때문에, 분자 네트워크가 기계적인 변종에 어떻게 반응하는지를 예측하는 것은 과학자들과 기술자들에게 지속적인 관심거리였다. 고무의 탄성 특성을 이해하기 위해서는 이론적으로 분자 수준에서 발생하는 물리적 메커니즘과 폴리머 체인의 무작위 보행 특성이 네트워크를 어떻게 정의하는지 둘 다 알 필요가 있다. 폴리머 체인의 짧은 부분 내에서 발생하는 물리적 메커니즘은 탄성력을 생성하며 네트워크 형태학은 이러한 힘이 결합하여 고무 샘플이 변형될 때(예: 인장 변형률에 의해) 관찰되는 거시적 응력을 생성하는 방법을 결정한다.

분자 수준 모형

실제로 고무 샘플이 늘어나면서 네트워크 체인 내에서 탄성력을 생성하는 몇 가지 물리적 메커니즘이 있다. 이 중 두 가지는 엔트로피 변화에서 발생하며, 한 가지는 체인 백본을 따라 분자 결합 각도의 왜곡과 관련이 있다. 이 세 가지 메커니즘은 적당한 두께의 고무 샘플을 수동으로 늘렸을 때 즉각적으로 드러난다. 처음에는 고무가 상당히 뻣뻣하게 느껴지는데, 즉, 변형률과 관련하여 높은 비율로 힘을 증가시켜야 한다. 중간 변종에서 필요한 힘의 증가는 같은 양의 스트레칭을 유발하기 위해 훨씬 더 낮다. 마지막으로, 표본이 파괴점에 가까워질수록 강성이 현저하게 증가한다. 관찰자가 알아차리고 있는 것은 다른 분자 메커니즘에 기인하는 탄성 계수의 변화다. 이러한 영역은 그림 1에서 볼 수 있는데, 천연고무에 대한 일반적인 응력 대 변형률 측정이다. 세 가지 메커니즘(Ia, Ib 및 II라는 라벨)은 주로 그림에 표시된 지역에 해당한다. 엔트로피의 개념은 상온에서의 고무 네트워크와 같은 대형 열 시스템의 연구와 관련된 통계적 역학이라고 불리는 영역 수학 물리학에서 우리에게 온다. 비록 구성 체인의 세부적인 행동이 무작위적이고 개별적으로 연구하기에는 너무 복잡하지만, 우리는 큰 표본의 통계적 역학 분석으로부터 그들의 '평균' 행동에 대한 매우 유용한 정보를 얻을 수 있다. 엔트로피 변화가 어떻게 우리의 일상 경험에서 힘을 만들어낼 수 있는지에 대한 다른 예는 없다. 폴리머 체인의 내향성 힘은 구성 원자가 주변 물질과 경험하는 열 충돌에서 발생하는 것으로 간주할 수 있다. 사슬이 곧게 될 수 밖에 없을 때 저항(탄력)력을 발생시키는 것은 바로 이 끊임없는 교전이다. 고무 샘플을 스트레칭하는 것이 탄력의 가장 흔한 예지만, 고무가 압축되었을 때도 발생한다. 압축은 풍선이 부풀어 오를 때와 같이 2차원 팽창이라고 생각할 수 있다. 탄성력을 생성하는 분자 메커니즘은 모든 종류의 스트레인에 대해 동일하다.

이러한 탄성력 모델을 네트워크의 복잡한 형태론과 결합하면, 거시적 응력을 예측하기 위한 단순한 분석 공식을 얻을 수 없다. 컴퓨터의 수치 시뮬레이션을 통해서만 분자 힘과 네트워크 형태학 사이의 복잡한 상호작용을 포착할 수 있어 고무 샘플이 경직될 때 응력과 궁극적인 고장을 예측할 수 있다.

고무탄성을^[4] 위한 분자결손 패러다임

Molecular Kink Paradise는 천연고무(폴리소프렌) 네트워크를 구성하는 분자 사슬이 주변 사슬에 의해 제한되어 '튜브' 안에 남는다는 직관적인 개념에서 발전한다. 어떤 적용된 변형률의 결과로서 체인에 생성되는 탄성력은 이 관 내의 체인 윤곽선을 따라 전파된다. 그림 2는 사슬의 인접 장치에 대한 연결을 나타내기 위해 각 끝단에 탄소 원자가 여분의 4-탄소 이소프렌 백본 장치의 표현을 나타낸다. 단일 C-C 채권 3개, 더블 본드 1개를 보유하고 있다. 폴리소프렌 체인이 그것의 가능한 순응을 무작위로 탐구하는 것은 주로 C-C 단일 결합에 대하여 회전하는 것이다. 두 개와 세 개 사이의 이솝렌 단위를 포함하는 체인의 섹션은 서로 통계적으로 상관관계가 없는 것으로 간주될 수 있을 정도로 충분한 유연성을 가지고 있다. 즉, 쿤 길이라고 하는 이 거리보다 더 큰 거리에 대해서는 체인을 따라 방향 상관관계가 없다. 이러한 비직선 지역들은 '끼익'의 개념을 환기시키고, 사실 사슬의 무작위 보행 성질의 발현이다. 콕은 각각 3개의 탄소-탄소 단일 결합을 가진 여러 이솝렌 단위로 구성되기 때문에, 콕에는 각각 뚜렷한 에너지와 종단간 거리를 가진 많은 가능한 순응이 있다. 몇 초에서 몇 분 사이의 시간 척도에서는 체인의 비교적 짧은 부분(즉, 꼬임)만 가능한 회전 순응 사이에서 자유롭게 이동할 수 있는 충분한 볼륨을 갖는다. 열 상호작용은 꼬인 부분이 가능한 모든 회전 순응 사이에서 전환되기 때문에 일정한 플럭스 상태로 유지되는 경향이 있다. 꼬인 부분이 열 평형 상태에 있기 때문에, 꼬인 부분이 회전 순응에 존재할 확률은 볼츠만 분포에 의해 주어지며, 엔트로피를 엔드 투 엔드 거리와 연관시킬 수 있다. 쿤 길이의 단대단 거리에 대한 확률 분포는 대략 가우스적이며 각 상태에 대한 볼츠만 확률 인자(회전 순응)에 의해 결정된다. 고무 네트워크가 늘어나면서, 일부 꼬임들은 엔드투엔드 거리가 더 큰 제한된 수의 더 확장된 순응으로 강요되고, 체인을 따라 탄성력을 생성하는 엔트로피의 감소 때문이다.

이러한 힘을 생성하는 분자 메커니즘은 세 가지가 있는데, 그 중 두 가지는 우리가 저사슬 확장 체제, Ia와^[5] 중간사슬 확장 체제 Ib라고 지칭할 엔트로피의 변화에서 발생한다.^[6] 세 번째 메커니즘은 등뼈를 따라 화학적 결합의 왜곡에 의해 초기 평형 등고선 길이를 초과하여 확장되기 때문에 고사슬 확장 시 발생한다. 이 경우 복원력은 봄과 같으며 우리는 그것을 체제 2라 칭할 것이다.^[7] 세 가지 힘 메커니즘은 그림 1과 같이 인장 응력 대 변형률 실험에서 관찰된 세 가지 영역에 대략 일치하는 것으로 확인된다.

네트워크의 초기 형태학은 화학적 교차 링크 직후에 두 가지 무작위 프로세스에 의해 관리된다.^[8][9] (1) 교차 링크가 어떤 이소프렌 단위에서 발생할 확률과, (2) 체인 순응의 무작위 보행 특성. 고정 체인 길이에 대한 단대단 거리 확률 분포(즉, 이솝렌 단위 고정 수)는 무작위 보행으로 설명된다. 네트워크 형태학을 특징짓는 것은 네트워크 체인 길이의 공동 확률 분포와 이들의 교차 링크 노드 사이의 엔드투엔드 거리다. 왜냐면, 실질적으로 탄성이 있는 힘과 네트워크의 복잡한 형태학을 생산하는 분자 물리학 메커니즘을 동시에 치료되어야 하며, 단순한 분석적 탄력성 모델;명백한 3차원 수치 model[10][11][12]긴장한 networ의 대표적인 볼륨 요소에 미치는 영향을 모사하기 위해서 필요하다 가능하지 않다.k

저사슬연장체제, Ia

Molecular Kink Paradise는 대표적인 네트워크 체인을 그것의 튜브 내의 체인 윤곽선을 따르는 일련의 벡터로서 구상하고 있다. 각 벡터는 꼬인 곳의 평형 끝에서 끝까지의 거리를 나타낸다. 모든 탄성력이 체인 윤곽선을 따라 작용한다고 가정하기 때문에 체인의 실제 3차원 경로는 적절하지 않다. 체인의 등고선 길이 외에도 유일한 중요한 매개변수는 고단도, 단대단 거리까지의 등고선 길이의 비율이다. 체인이 확장될 때 가해진 스트레인에 반응하여 유도 탄성력은 그 윤곽선을 따라 균일하게 확산되는 것으로 가정한다. 엔드 포인트(네트워크 노드)가 인장 변형률 축과 어느 정도 정렬된 네트워크 체인을 고려하십시오. 고무 샘플에 초기 변형률을 적용하면 체인 끝의 네트워크 노드가 분리되기 시작하고 윤곽선을 따라 모든 꼬인 벡터가 동시에 늘어나게 된다. 물리적으로 적용된 변형률로 인해 꼬인 부분이 열 평형 거리를 넘어 늘어나 엔트로피가 감소한다. 엔트로피의 이러한 변화와 관련된 자유 에너지의 증가는 스트레인에 반대되는 (선형) 탄성력을 발생시킨다. 저변형 체계에 대한 힘의 상수는 관련 온도(예: 300K)에서 2-3개의 이솝렌 단위로 구성된 짧은 체인의 꼬임 궤적을 샘플링하여 추정할 수 있다.^[5] 시뮬레이션 과정에 걸쳐 좌표의 많은 표본을 추출함으로써 꼬임에 대한 단대단 거리의 확률 분포를 얻을 수 있다. 이러한 분포(약 가우스파인 것으로 판명된)는 상태 수와 직접 관련되므로, 우리는 어떤 단대단 거리에서도 꼬임 엔트로피와 연관시킬 수 있다. 확률 분포, 엔트로피 및 자유 에너지의 변화를 숫자로 구분함으로써 꼬인 단대단 거리에 대한 변화를 찾을 수 있다. 이 정권에 대한 힘 모델은 선형이며 온도에서 사슬의 고단도로 나눈 값과 비례하는 것으로 밝혀졌다.

중도사슬연장체제, Ib

저연장 체제의 어느 시점에서는, 즉 체인을 따라 있는 모든 꼬임들이 동시에 연장되고 있기 때문에 체인을 더 연장하기 위해 연장된 순응으로 한 번의 꼬임 전환을 하는 것이 정력적으로 더 유리해진다. 적용된 스트레인은 꼬임 내의 단일 이솝렌 장치를 확장된 순응으로 강제할 수 있으며, 체인의 단대단 거리를 약간 증가시킬 수 있으며, 이를 위해 필요한 에너지는 모든 꼬임들을 동시에 계속 연장하는 데 필요한 에너지보다 적다. 수많은 실험은^[13] 고무망을 스트레칭하는 것이 엔트로피 감소와 동반한다는 것을 강력히 시사한다. 그림 2와 같이, 이솝렌 유닛은 3개의 단일 C-C 결합을 가지고 있으며, 에너지 미니마(minima)를 갖는 이들 결합에 대해 2, 3개의 선호 회전각(방향)이 있다. 허용된 회전^[6] 순응 18개 중 단 6개만이 단대단 거리를 연장했으며 체인의 이소프렌 장치가 확장 상태의 일부 하위 집합에 상주하도록 강제하는 것은 열 동작에 사용할 수 있는 회전 순응의 수를 줄여야 한다. 엔트로피를 감소시키는 것은 가용 상태 수의 감소다. 체인이 계속 똑바르게 되면서 체인에 있는 모든 이솝렌 장치는 결국 연장된 순응으로 강제되어 체인은 '조용한' 것으로 간주된다. 체인 확장에 대한 힘 상수는 이 엔트로피 변화와 관련된 자유 에너지의 결과적 변화로부터 추정할 수 있다.^[6] 이아 체제와 마찬가지로 이 체제의 힘 모델은 선형이며, 사슬의 고단도로 나눈 온도에 비례한다.

하이 체인 확장 시스템, II

네트워크 체인의 모든 이소프렌 장치가 단지 몇 번의 연장된 회전 순응으로 상주하도록 강요되었을 때 체인은 팽팽해진다. C-C 본드가 체인 윤곽선을 따라 만드는 지그재그 경로를 제외하면 감각적으로 직선이라고 볼 수 있다. 단, 결합각 증가, 결합 스트레칭 및 이음각 회전과 같은 결합 왜곡에 의해 추가 연장이 여전히 가능하다. 이러한 힘은 봄과 같으며 엔트로피 변화와 관련이 없다. 팽팽한 체인은 40% 정도만 연장할 수 있다. 이 지점에서 체인을 따르는 힘은 C-C 공밸런트 결합을 기계적으로 파열시키기에 충분하다. 이 인장력 한계는 양자 화학 시뮬레이션을 통해 계산되었으며^[7], 약 7nN으로, 낮은 변형률에서 이방성 연쇄 힘보다 약 1,000배 더 크다. 이소프렌 단위에서 인접한 백본 C-C 결합 사이의 각도는 약 115–120도 사이에 다양하며 이러한 각도를 유지하는 것과 관련된 힘은 상당히 크기 때문에 각 단위 내에서 체인 백본은 결합 파열 시에도 항상 지그재그 경로를 따른다. 이 메커니즘은 높은 변종에서 관찰되는 탄성 응력의 가파른 상승을 설명한다(그림 1).

네트워크 형태학

네트워크는 단 2개의 파라미터(단위 볼륨당 네트워크 노드의 수와 폴리머의 통계적 탈상관화 길이, 쿤 길이)에 의해서만 완전히 설명되지만, 체인이 연결되는 방식은 실제로 상당히 복잡하다. 체인의 길이가 크게 달라져 있으며, 대부분은 가장 가까운 이웃 네트워크 노드에 연결되지 않는다. 체인 길이와 그것의 종단간 거리는 모두 확률 분포로 설명된다. '형질학'이라는 용어는 이러한 복잡성을 가리킨다. 크로스링크제(cross-linking agent)가 철저히 섞이면, 어떤 이소프렌 단위라도 네트워크 노드가 될 확률은 동등하다. 과산화디쿠밀의 경우 천연고무에서 효율을 연결하는 교차 연결은 통일성이지만 유황의 경우는 그렇지 않다.^[14][15] 네트워크의 초기 형태학은 두 가지 무작위 프로세스에 의해 지시된다. 즉, 어떤 이솝렌 단위에서든 크로스 링크가 발생할 확률과 체인 순응의 마르코프 무작위 보행 특성이다.^[8][9] 체인 끝의 한쪽 끝이 다른 쪽 끝에서 얼마나 멀리 '뒤틀릴 수 있는지'에 대한 확률 분포 함수는 마르코프 시퀀스에 의해 생성된다.^[16] 이 조건부 확률밀도함수는 $쿤{\displaystyle }$ $길이{\displaystyle }$ b ${\displaystyle b}$과(와$$) 단위의 체인 길이 $n{\displaystyle }${\$displaystyle n}$을(를) 종단간 거리 r ${\displaystyle r}$에 관련시킨다$.$

${\displaystyle P(r n)=4\pi r^{2}\lift({2nb^{2}\pi }{3}\{3}\right)^{-{\frac {3}}\expleft(-{3r^{2}}:{2nb^{2}}\}\오른쪽)\,},},},},}$

(1)

모든 이솝렌 단위가 크로스 링크 노드의 일부가 될 확률은 이솝렌 단위 대비 크로스 링크 분자(예: 디큐밀-과산화수소)의 농도의 비율에 비례한다.

${\displaystyle p_{x}=2{\frac{{\text{cross-link}}}}{{\text{isopreen}}}}}}}$

이소프렌 단위 2개(각 체인의 1개)가 크로스링크에 참여하기 때문에 2개 요인이 발생한다. $N{\displaystyle }$ ${\displaystyle N}$ 이솝렌$$ 단위를 포함하는 체인을 찾을 확률은 다음과 같다.

${\displaystyle P(N)=p_{x}{\왼쪽(1-p_{x}\오른쪽)^{{N-1}\}$

(3)

여기서 $N{\displaystyle }$ ${\displaystyle \ge }$ ${\displaystyle 1}$ ${\displaystyle N\geq 1$ 이 등식은 단순히 이소프렌 단위가 체인을 따라 N-1 연속 단위의 교차 링크(1-p_x)가 아닐 확률로 이해할 수 있다. N과 함께 P(N)가 감소하기 때문에, 짧은 체인은 긴 체인에 비해 개연성이 높다. 통계적으로 독립적인 백본 세그먼트의 수가 이솝렌 단위 수와 같지 않다는 점에 유의하십시오. 천연 고무 네트워크의 경우, 쿤 길이에는 약 2.2 이소프렌 단위가 포함되어 있으므로,${\displaystyle \mathrm{N}}$~ 2.${\displaystyle \mathrm{2n}}${\$displaystyle$ N$\sim$ 2.$2n$ 네트워크 체인 길이$($${\displaystyle }$ ${\displaysty$N$\})$와 종단간 거리(종단간 ${\displaystyle }$ ${\displaysty$ r$})$와 관련된 방정식 (1)과 (3)(공동 확률 분포)의 산물이다.크로스 링크 노드:

${\displaystyle P(r,N)\;=\;P(N)P(r N)\;=\;p_{x}{\left(1-p_{x}\right)}^{N-1}\,4\pi r^{2}\left({\frac {2nb^{2}\pi }{3}}\right)^{-{\frac {3}{2}}}\exp \left(-{\frac {3r^{2}}{2nb^{2}}}\right)}$

(4)

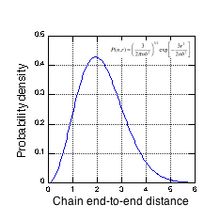
천연 고무 네트워크의 복잡한 형태학은 그림 3에서 볼 수 있는데, 이것은 '평균' 체인의 확률밀도 대 (평균 노드 간격 단위)를 나타낸다. 일반적인 실험 교차 링크⁻³ 밀도 4x10¹⁹ cm의 경우, 평균 체인은 약 116개의 이소프렌 단위(52 Kuhn 길이)를 포함하고 있으며 등고선 길이는 약 50 nm이다. 그림 3은 체인의 상당 부분이 여러 노드 스페이스에 걸쳐 있음을 보여준다. 즉, 체인의 끝은 다른 네트워크 체인과 겹친다. 천연고무는 과산화디쿠밀과 교차연결이 되어 있으며, 테트라 기능 교차연결이 있다. 즉, 각 교차연동 노드는 그것에서 나오는 4개의 네트워크 체인을 가지고 있다. 변형률 축에 대한 초기 역도와 끝점의 방향에 따라, 활성 교차 링크 노드와 관련된 각 체인은 적용된 변형률에 저항할 때 서로 다른 탄성력 상수를 가질 수 있다. 각 교차 링크 노드의 힘 평형(순력 0)을 유지하기 위해, 노드는 체인 확장에 대한 가장 높은 힘 상수를 가진 체인과 함께 동시에 이동하도록 강제될 수 있다. 고무 네트워크의 기계적 특성에 대한 연구를 매우 어렵게 만드는 것은 네트워크 형태학의 무작위적 특성에서 발생하는 이 복잡한 노드 운동이다. 네트워크가 경색됨에 따라, 이렇게 더 확장된 체인으로 구성된 경로가 전체 샘플에 걸쳐 나타나며, 이러한 경로들이 높은 스트레스의 대부분을 전달한다.

수치 네트워크 시뮬레이션 모델

고무 샘플의 탄성 응답을 계산하려면 3개의 체인 힘 모델(시간: Ia, Ib, II)과 네트워크 형태학이 마이크로 기계식 네트워크 모델에서 결합되어야 한다.^[10][11][12] 등식 (4)의 관절 확률 분포와 힘 확장 모델을 사용하여, 네트워크의 충실한 대표 체적 요소를 구성하고, 스트레인에 노출될 때 발생하는 기계적 응력을 시뮬레이션하기 위한 수치 알고리즘을 고안하는 것이 가능하다. 반복적 이완 알고리즘은 스트레인이 가해질 때 각 네트워크 노드에서 근사적인 힘의 평형을 유지하기 위해 사용된다. 2 또는 3개의 이소프렌 단위(약 1 Kuhn 길이)를 가진 꼬임에 대해 얻은 힘 상수를 수치 시뮬레이션에서 사용할 때 예측 응력은 실험과 일치하는 것으로 확인된다. 그러한 계산^[15] 결과는 그림 1(빨간색 선)에 황 교차 연결 천연 고무에 대해 표시되며 실험 데이터^[17](단색 파란색 선)와 비교된다. 또한 이러한 시뮬레이션은 네트워크 체인이 팽팽해지고 궁극적으로 결합 파열로 인한 물질적 고장으로 인해 스트레스가 급격히 상승할 것으로 예측한다. 유황 교차연계 천연고무의 경우 교차연계 내 S-S 본드는 체인 백본에 있는 C-C 본드보다 훨씬 약하며 네트워크 장애 지점이다. 시뮬레이션된 응력에서 고원은 약 7의 변형률에서 시작하여 네트워크의 한계값이다. 약 7 MPa 이상의 스트레스는 지원할 수 없으며 네트워크가 실패한다. 이 스트레스 제한에 근접하여 시뮬레이션에서는 10% 미만의 체인이 팽팽하다고 예측한다^[12]. 즉, 높은 체인 확장 체제에서 체인은 0.1% 미만이 파열되었다. 매우 낮은 파열 분율이 놀라워 보일지 모르지만, 그것은 고무 밴드가 부서질 때까지 스트레칭한 우리의 경험과 일치하지 않는다. 깨진 후 고무의 탄성 반응은 원래와 눈에 띄게 다르지 않다.

실험

인장응력과 온도의 변화

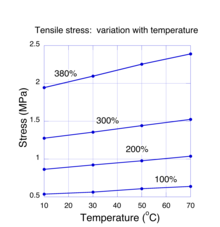
열 평형에 있는 분자 시스템의 경우, 에너지의 추가. 예: 기계적 작업에 의해 엔트로피 변화를 일으킬 수 있다. 이것은 열역학 이론과 통계 역학 이론에서 알 수 있다. 구체적으로, 두 이론 모두 에너지의 변화는 엔트로피 변화 시간 절대 온도에 비례해야 한다고 주장한다. 이 규칙은 에너지가 분자의 열 상태로 제한되는 경우에만 유효하다. 고무 샘플이 충분히 늘어나면 에너지가 화학적 결합의 왜곡과 같은 비열 상태에 존재할 수 있고 규칙이 적용되지 않는다. 저-중간 변종에서 이론은 필요한 스트레칭 힘은 네트워크 체인의 엔트로피 변화 때문이라고 예측한다. 만약 이것이 맞다면, 우리는 샘플을 스트레인 값으로 늘리기 위해 필요한 힘은 샘플의 온도에 비례해야 한다고 예상한다. 늘어난 고무 표본의 인장응력이 온도에 따라 어떻게 변화하는지 보여주는 측정치는 그림 4와 같다. 이러한 실험에서는 10~70도의 온도 변화에 따라 늘어난 고무 표본의 변형률이 고정된 상태로 유지되었다.^[18] 고정 변형률의 각 값에 대해 인장 응력이 (실험 오차 내에서) 선형적으로 변화했다고 본다. 이러한 실험은 엔트로피 변화가 고무 탄력의 근본적인 메커니즘이라는 가장 설득력 있는 증거를 제공한다. 온도에 따른 스트레스의 양의 선형행동은 때때로 고무가 열팽창 계수가 음수라는 잘못된 개념으로 이어진다. 즉, 표본의 길이가 가열될 때 수축된다. 실험^[19] 결과, 거의 모든 다른 재료와 마찬가지로 열팽창 천연고무의 계수가 양수임을 결정적으로 밝혀냈다.

스냅백 속도

고무줄과 같은 고무줄을 늘일 때, 우리는 고무줄이 균일하게, 세로 방향으로 변형된다는 것을 알아차린다. 길이를 따라 있는 모든 원소는 전체 표본과 동일한 확장 계수를 경험한다. 만약 우리가 한쪽 끝을 놓으면, 샘플은 원래의 길이로 빠르게 되돌아가는데, 우리의 눈이 그 과정을 해결하기에 너무 빠르다. 우리의 직관적인 기대는 그것이 늘었을 때와 같은 방식으로, 즉 일률적으로 원래의 길이로 되돌아온다는 것이다. 그러나 이런 일은 일어나지 않는다. Mrowca 등의 실험적인 관찰은 놀라운 행동을 보여준다.^[20] 극도로 빠른 수축 역학을 포착하기 위해 그들은 고속 전자 측정 장치가 발명되기 훨씬 전인 1874년 엑너와 스테판이^[21] 고안한 교묘한 실험 방법을 활용했다. 그들의 방법은 빠르게 회전하는 유리 실린더로 구성되어 있었는데, 그것은 램프 블랙으로 코팅된 후 늘어난 고무 샘플 옆에 놓였다. 고무 샘플의 중간점과 자유단에 부착된 스틸리는 유리 실린더와 접촉하여 고정되었다. 그런 다음 고무의 자유단이 다시 끊어질 때 스타일리는 회전 실린더의 램프 블랙 코팅에서 나선 경로를 추적했다. 실린더의 회전 속도를 조절함으로써 하나의 완전한 회전 이하로 스타일리의 위치를 기록할 수 있었다. 그 궤적은 습한 블로터 종이에 실린 실린더를 굴려 그래프로 옮겨졌다. 스타일러스가 남긴 마크는 종이에 흰색 선(램프 블랙은 없음)으로 나타났다. 그림 5의 그래프로 표시된 그들의 데이터는 표본이 원래 길이로 빠르게 수축할 때 끝과 중간점 스타일리의 위치를 보여준다. 표본은 처음에 구속되지 않은 길이를 초과하여 9.5"로 늘렸다가 방출되었다. 스타일리는 6ms 조금 넘는 시간에 원래 위치로 돌아왔다. 변위 대 시간의 선형 거동은 짧은 가속 후 표본의 끝과 중간점이 약 50m/s 또는 112mph의 등속도로 스냅된 것을 나타낸다. 그러나 중간점 스타일러스는 종료 후 약 3ms가 지나서야 움직이기 시작했다. 분명히, 수축 과정은 자유 끝에서 시작하여 파동으로 이동한다. 하이 익스텐션에서, 늘어난 네트워크 체인에 저장된 에너지의 일부는 엔트로피의 변화로 인한 것이지만, 대부분의 에너지는 엔트로피 변화를 수반하지 않는 본드 왜곡(레지메 II, 위)에 저장된다. 저장된 모든 에너지가 운동 에너지로 변환된다고 가정할 경우, 익숙한 보존 방정식 E= ½ mv에서² 직접 수축 속도를 계산할 수 있다. Molecular Kink 패러다임에 기초한 ^[11]수치 시뮬레이션은 이 실험과 일치하는 속도를 예측한다.

탄력성 이론에 대한 역사적 접근법

유진 거스(Eugene Guth)와 휴버트 M. 제임스는 1941년에 고무 탄성의 등방성 기원을 제안했다.^[22]

열역학

온도는 엘라스토머의 탄력에 특이한 방식으로 영향을 미친다. 탄성체가 스트레치 상태에 있다고 가정할 때, 가열은 탄성체를 수축시킨다. 반대로 냉각은 팽창의 원인이 될 수 있다.^[23] 이것은 보통의 고무줄로 관찰할 수 있다. 고무줄을 늘리면 열을 방출하고(입술에 대고 누른다) 스트레칭 후 풀어주면 열을 흡수해 주변이 시원해진다. 이 현상은 깁스 자유 에너지로 설명할 수 있다. ΔG=ΔH-tΔS의 재배열, 여기서 G는 자유 에너지, H는 엔탈피, S는 엔트로피, 우리는 ΔS=ΔH-ΔG를 얻는다. 스트레칭은 피로가 없기 때문에 외부 작업이 필요하기 때문에 TΔS는 음수여야 한다. T는 항상 양(절대 0에 도달할 수 없음)이므로 ΔS는 음(-)이어야 하며, 이는 장력을 받을 때보다 자연 상태의 고무가 더 많이 얽혀 있음을 암시한다. 따라서 장력이 제거되면 반응이 자발적이어서 ΔG가 음이 된다. 따라서 냉각 효과는 양수 ΔH를 나타내야 하므로 ΔS는 양수일 것이다.^[24][25]

그 결과 탄성체는 이상적인 단원자 기체처럼 작용하게 되는데, (좋은 근사치까지) 탄성 중합체는 그 위에 작업이 수행되었을 때 늘어난 화학 결합이나 스트레칭 분자에서 수행된 탄성 작업에 어떠한 잠재적 에너지도 저장하지 않기 때문이다. 대신 고무에 대한 모든 작업은 "해제"(저장되지 않음)되며, 즉시 폴리머에 열 에너지로 나타난다. 같은 방법으로 탄성체가 주위에 하는 모든 작업은 일을 하기 위해 열 에너지가 사라지는 결과를 초래한다(탄성 띠는 팽창하는 가스처럼 차가워진다). 이 마지막 현상은 (이상적인 기체와 마찬가지로) 엘라스토머의 능력이 오직 엔트로피 변화 고려사항에만 의존하고 폴리머 결합 내에 저장된 (즉, 잠재적) 에너지에 의존하지 않는다는 결정적인 단서다. 그 대신 일을 하기 위한 에너지는 전적으로 열에너지에서 나오며, (이상 기체가 팽창하는 경우처럼) 고분자의 양의 엔트로피 변화만이 내부 열 에너지를 효율적으로(이론적으로 100%) 작업으로 변환할 수 있게 한다.

폴리머 체인 이론

고무탄성 이론을 환기시키면서 교차연계망의 폴리머 체인을 이방성 스프링으로 간주한다. 체인을 늘리면, 사용할 수 있는 순응이 적기 때문에 엔트로피가 큰 폭으로 감소한다.^[26] 따라서 복원력이 있어 외부력이 제거되면 고분자 체인이 높은 엔트로피 무작위 코일 구성과 같이 평형이나 확장되지 않은 상태로 되돌아간다. 고무밴드가 원상태로 돌아가는 이유다. 고무탄력성을 위한 두 가지 일반적인 모델은 자유롭게 접합된 체인 모델과 웜처럼 생긴 체인 모델이다.

자유 접합 체인 모델

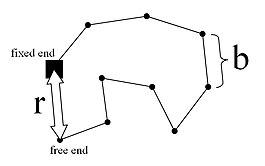
이상적인 체인이라고도 불리는 자유 결합 체인은 무작위 보행 모델을 따른다. 현미경적으로 폴리머 체인의 3-D 무작위 보행은 전체 단대단 거리가 x, y, z 방향으로 표현된다고 가정한다.

${\textstyle {\vec{R}=R_{x}{\hat {x}+R_{y}{\hat{y}}+R_{z}{\hat {z}}$

In the model, ${\displaystyle b\,}$ is the length of a rigid segment, ${\displaystyle N\,}$ is the number of segments of length ${\displaystyle b\,}$, ${\displaystyle R\,}$ is the distance between the fixed and free ends, and ${\displaystyle L_{\rm {c}}\,}$ is the "contour length" or ${$$\displaystyle Nb$유리 전환 온도 위에서는 폴리머 체인이 진동하고 $r{\displaystyle }$ ${\$ r$\,}$ 시간이 지남에 따라 변화한다$$. 체인의 확률 분포는 다음과 같은 가우스 분포로 주어진 개별 성분의 확률 분포의 산물이다.

${\displaystyle P({\vec {R}})=P(R_{x})P(R_{y})P(R_{z})=\left({\frac {2nb^{2}\pi }{3}}\right)^{-{\frac {3}{2}}}\exp \left({\frac {-3R^{2}}{2Nb^{2}}}\right)\,}$

따라서 앙상블 평균 단대단 거리는 모든 공간에 걸친 확률 분포의 표준 적분일 뿐이다. 이동은 뒤로 또는 앞으로 이동할 수 있으므로 순 평균${\displaystyle }$average ${\displaystyle R}$ ${\displaystyle ⟩}$ ${\displaystyle \langle R\angle }$은(는) 0이 될 수 있다는$$ 점에 유의하십시오. 그러나 거리의 유용한 척도로 루트 평균 제곱을 사용할 수 있다.

${\displaystyle {\begin}\langle R\rangele &=0\\\\langle R^{2}\=nb^{2}\langle R^{1}{1}{1}{{{{N}b\end}}}}}}}}}}$ ${\displaystyle \langle R^{2}\angle =\int \limits _{0}^{\nft }R^{2}4\pi R^{2}P({\vec{R}})dR=Nb^{2}}:$

고무탄력성의 플로리 이론은 고무탄력성이 주로 이방성 기원을 가지고 있다는 점을 지적해 왔다. 헬름홀츠 자유 에너지와 엔트로피에 대한 논의에 대해 다음과 같은 기본 방정식을 사용함으로써, 원래 펴지지 않은 순응으로부터 고무 체인의 변형에서 발생하는 힘을 도출할 수 있다. $\Omega {\displaystyle \mathrm{}}$ ${\displaystyle \Oomega}$은(는) 폴리머 체인의 순응 수입니다. Since the deformation does not involve enthalpy change, the change in free energy can just be calculated as the change in entropy${\displaystyle -T\Delta S}$. It can be observed that the force equation resembles the behavior of a spring and follows Hooke's law:${\displaystyle F=kx}$, where F is the force, k is the spring 상수와 x는 거리다. 일반적으로 네오후크식 모델은 교차 연결된 폴리머에 사용되어 스트레스 변형 관계를 예측할 수 있다.

${\displaystyle \Oba =C\exp \left({\frac {-3{\vec{R}^{2}}:{2Nb^{2}}\오른쪽)}}$

${\displaystyle S=k_{\rm {{B}\ln \Oba \,\frac {-3k_{\rm{B}}{\vec{R}^{2}}:{2Nb^{2}}:$

${\displaystyle \Delta F({\vec {R}})\대략 -T\Delta S_{d}({\vec {R}^{2})=C+{\frac {3k_{\rm{B}}}T}{Nb^{2}}:{\vec{R}^{2}}:$

${\displaystyle f={\frac {dF({\vec{R}})}{d{\vec {R}}={d}{\vec {R}}}}{\frac {3k_{B}}T{{\vec{R}^{2}}:{2Nb^{2}}={\frac {3k_{B}T}{Nb^{2}}:{\vec{R}}}$

탄성계수 ${\displaystyle {}_{}}$ ${\displaystyle {B\mathrm{}}_{}}$ ${\displaystyle T_{}/N}$ b ${\displaystyle 3k_{\rm {B}T/Nb}$은(는) 온도에 따라 다르다는$$ 점에 유의하십시오. 고무 온도를 높이면 탄성계수도 올라간다. 일정한 스트레스를 받는 고무의 온도가 올라가면 수축하는 이유다.

우리는 플로리 이론을 더 확대해서 벌크 고무 재료가 논의되는 거시적인 시각으로 볼 수 있다. 고무 재질의 원래 치수가 ${\displaystyle L_{}}$ $x{\displaystyle {}_{}}$ ${\$ ${\displaystyle L_{}}$ ${\displaystyle y_{}}$ ${\$ $L$ z ${\$$displaystyle L_{z}$라고 가정하면 길이(${\displaystyle {}_{}}$ ${\displaystyle x_{}}$ L ${\displaystyle x_{}}$ ${\$ $\lambda _{i})$에 개별 연장비를 적용하여 변형 형태를 표현할 수 있다$.$$tyle \lambda _{x}L_{x}},$$\lambda {\displaystyle {}_{}}$ ${\displaystyle y_{}}$ L ${\displaystyle y_{}}$ ${\$$L_{y}}},$$\lambda {\displaystyle {}_{}}$ ${\displaystyle z_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\displaystyle z_{}}$ ${\$ 그래서 현미경으로 보면 기형적인 폴리머 체인은 확장 비율로도 표현할 수 있다: : x ${\displaystyle R_{}}$ ${\displaystyle {}_{}{}_{}}$ ${\$$R_{$$x}},$$\lambda {\displaystyle {}_{}}$ ${\displaystyle y_{}}$ ${\displaystyle R_{}}$ ${\$ $_{$$y}}},$${\displaystyle {\lambda }_{}}$ ${\displaystyle {}_{}{}_{}}${\$displaystyle \lambda$ \lambda_${{{$lambda}R_}$R_$ 변형으로 인한 자유 에너지 변화는 다음과 같이 표현할 수 있다.

${\displaystyle {\begin{aigned}\Delta F_{\text}{def}({\vec {R}})&=-{\frac {3k_{B}T{\vec {R}}^{2}}{2Nb^{2}}}=-{\frac {3k_{B}T((R_{x}^{2}-R_{x0}^{2})+(R_{y}^{2}-R_{y0}^{2})+(R_{z}^{2}-R_{z0}^{2}))}{2Nb^{2}}}\\&=-{\frac {3k_{B}T((\lambda _{x}^{2}-1)R_{x0}^{2})+(\lambda _{y}^{2}-1)R_{y0}^{2}+(\lambda _{z}^{2}-1)R_{z0}^{2}}{2Nb^{2}}}\end{arged}}}}}}}}$

고무가 교차 연결되고 등방성이 있다고 가정하면 무작위 보행 모델은 $R{\displaystyle {}_{}}$ x ${\$ $스타일 R_{x},$ R ${\displaystyle y_{}}$ ${\$ 스타일 $R_{y},$ R ${\displaystyle z_{}}$ ${\$ 스타일 $R_{z}}$을(를) 정상 분포에 따라 분포한다$$. Therefore, they are equal in space, and all of them are 1/3 of the overall end-to-end distance of the chain: ${\displaystyle \langle R_{x0}^{2}\rangle =\langle R_{y0}^{2}\rangle =\langle R_{z0}^{2}\rangle =\langle R^{2}\rangle /3}$. Plugging in the change of free e위의 Nergy 방정식은 다음을 쉽게 얻을 수 있다.

${\displaystyle {\begin{aligned}\Delta F_{\text{def}}({\vec {R}})&=-{\frac {k_{B}Tn_{s}\langle R^{2}\rangle (\lambda _{x}^{2}+\lambda _{y}^{2}+\lambda _{z}^{2}-3)}{2Nb^{2}}}\\&=-{\frac {k_{B}Tn_{s}\langle R^{2}\rangle (\lambda _{x}^{2}+\lambda _{y}^{2}+\lambda _{z}^{2}-3)}{2R_{0}^{2}}\\\end{aigned}}}$

볼륨당 자유 에너지 변화는 다음과 같다.

${\displaystyle \Delta f_{\text{def}}={\frac {\Delta F_{\text{def}}({\vec {R}})}{V}}=-{\frac {k_{B}Tv_{s}\beta (\lambda _{x}^{2}+\lambda _{y}^{2}+\lambda _{z}^{2}-3)}{2}}}$

where ${\displaystyle n_{s}}$ is the number of strands in network, the subscript ${\displaystyle {\text{def}}}$ means "deformation", ${\displaystyle v_{s}=n_{s}/V}$, which is the number density per volume of polymer chains, ${\displaystyle \beta =\langle R^$${2}\rangele /R_{0}^{2}}:$ 체인의 종단간 거리와 무작위 보행 통계를 따르는 이론적 거리 사이의 비율이다$$. 우리가 비압축성을 가정할 경우 확장 비율의 곱은 1이며, 이는 볼륨의 변화가 없음을 의미한다: ${\displaystyle {\lambda }_{}}$ x ${\displaystyle {}_{}{}_{}}$ ${\displaystyle y_{}}$ ${\displaystyle {\lambda }_{}}$ z${\displaystyle {}_{}}$= ${\displaystyle 1}$ ${\displaystyle \lambda _{x}\lambda _{y}\lambda _{z}=1$

사례 연구: 일축 변형:

In a uniaxial deformed rubber, because ${\displaystyle \lambda _{x}\lambda _{y}\lambda _{z}=1}$ we assume ${\displaystyle \lambda _{x}=\lambda _{y}=\lambda _{z}^{-1/2}}$ . So the previous free energy per volume equation is:

${\displaystyle \Delta f_{\text{def}}={\frac {\Delta F_{\text{def}}({\vec {R}})}{V}}=-{\frac {k_{B}Tv_{s}\beta (\lambda _{x}^{2}+\lambda _{y}^{2}+\lambda _{z}^{2}-3)}{2}}={\frac {k_{B}Tv_{s}\beta }{2}}(\lambda _{z}^{2}+{\frac {2}{\lambda _{z}}}-3)}$

공학적 응력(정의에 의한)은 연장비 측면에서 에너지의 첫 번째 파생상품으로, 스트레인의 개념과 동일하다.

${\displaystyle \sigma _{eng}={\frac {d(\Delta f_{\text{def})}{\lambda _{z}}=k_{B}}Tv_{s}\beta(\lambda _{z}-{\frac {1}{\lambda _{z}^{2}}})$

그리고 영의 Modulus $E{\displaystyle }$ ${\displaystyle E}$은 변형률에 대한 응력의 파생물로 정의되며, 이는 실험실 실험에서 고무의 강성을 측정한다.

${\displaystyle E={\frac {d(\sigma _{eng})}}{d\lambda _{z}=k_{B}Tv_{s}\beta(1+{\frac {2}{\lambda _{z}^{3}}) _{\lambda _{z}=1}=1k_{B}}}TV_{s}\beta ={\frac {3\rho \beta RT}{M_{s}}}}}}}}}}$

여기서 $v{\displaystyle {}_{}}$ ${\displaystyle s_{}}$= ${\displaystyle \rho }$ ${\displaystyle N_{}}$ ${\displaystyle {}_{}}$/ ${\displaystyle M_{}}$ ${\displaystyle s{}_{}}$ ${\$$\rho {\displaystyle }$ ${\displaystyle \rho}}}$은 체인의 질량 밀도$$, M ${\displaystyle s_{}}$ ${\$은 교차$$ 링크 사이의 네트워크 스트랜드의 평균 분자량이다. 여기서, 이러한 유형의^[27] 분석은 고무 탄성의 열역학 이론을 실험적으로 측정할 수 있는 매개변수와 연결한다. 게다가, 그것은 재료의 교차 링크 조건을 볼 수 있게 해준다.

웜 유사 체인 모델

웜 같은 체인 모델(WLC)은 분자를 구부리는 데 필요한 에너지를 고려한다. 지속성 길이인$$$L{\displaystyle {}_{}}$ ${\displaystyle {p\mathrm{}}_{}}$ ${\$ $L_{\rm {p$$}\,}$을(를) 제외하고 변수는 동일하다$.$ $그러면$ 힘은 $다음{\displaystyle }$ 방정식을 따른다.

${\displaystyle F\ 약 {\frac {k_{\rm {B}}T}{{L_{\rm{p}}}}\좌({\frac {1}{1-{\frac {1}{{\rm{c}}\우)^{2}}-{\frac {1}{1}{4}+{{{L_\rm{c}}}\우),},},},},}$

따라서 체인 끝 사이의 거리(r=0)가 없을 때, 그렇게 하는 데 필요한 힘은 0이며, 폴리머 체인(${\displaystyle }$= ${\displaystyle {L\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ $displaystyle r=L_{\rm{c}\,})$을 완전히 연장하기 위해서는 무한의 힘이 필요하며, 이는 직관적이다. 그래픽적으로 힘은 원점에서 시작되며 처음에는 $r{\displaystyle }$ ${\displaystyle$ r$}$과 함께 선형적으로 증가한다$.$ 그 후 힘은 고공이지만 결국 다시 증가하여 체인 길이가 ${\displaystyle {L\mathrm{}}_{}}$ c ${\$에 가까워질 때 무한대에 접근한다$.$

참고 항목

• 탄력성(물리학)
• 과대성 소재
• 폴리머
• 열역학

참조