과대성 소재

다음에 대한 시리즈 일부
연속체 역학
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ 픽의 확산 법칙
법 컨버지 미사 모멘텀 에너지 불평등 클라우시우스-듀헴 (엔트로피)
고체 역학 변형 탄력성 일직선의 가소성 후크의 법칙 스트레스 유한변형 무한 변형률 호환성. 벤딩 접촉 역학 마찰의 물질적 고장 이론 파단 역학
유체역학 유체 통계학 · 역학 아르키메데스의 원리 · 베르누이의 원리 나비에-스토크스 방정식 푸아세유 방정식 · 파스칼의 법칙 점도 (뉴턴어 · 비뉴턴어) 부력 · 믹싱 · 압력 액체 접착 모세관 작용 크로마토그래피 응집(화학) 표면장력 가스 대기 보일의 법칙 찰스의 법칙 복합가스법 픽의 법칙 게이 루삭의 법칙 그레이엄의 법칙 플라즈마
리히로지 점탄성 레호메트리 레히미터 스마트 유체 전기오류 자기 지질학 페로플루이드
과학자들 베르누이 보일 카우치 찰스 오일러 픽 게이 루삭 그레이엄 훅 뉴턴 나비에르 노울 파스칼 스톡스 트뤼셀
v t

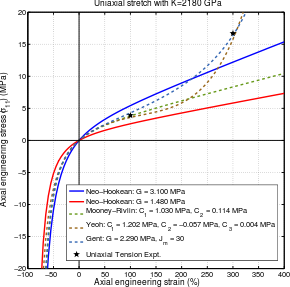
과급성 물질 또는 녹색 탄성 물질은^[1] 응력-스트레인 관계가 변형 에너지 밀도 함수에서 발생하는 이상적으로 탄성 있는 물질에 대한 구성 모델의 한 유형이다. 과대성 물질은 코시 탄성 물질의 특별한 경우다.

많은 재료의 경우 선형 탄성 모델은 관측된 재료의 행동을 정확하게 설명하지 않는다. 이러한 종류의 재료의 가장 일반적인 예는 고무인데, 고무의 응력 변형 관계는 비선형 탄성, 등방성, 비압축성 및 일반적으로 변형률과 독립적으로 정의될 수 있다. 과대역성(hyperperactity)은 그러한 재료의 응력 변형 행동을 모델링하는 수단을 제공한다.^[2] 미충전, 경화탄성 탄성체의 행동은 종종 과대망상적 이상과 밀접하게 일치한다. 충만 탄성계와 생물학적^[3][4] 조직도 과대증적 이상화를 통해 모델링되는 경우가 많다.

로널드 리블린과 멜빈 무니는 최초의 과대망상 모델인 네오후크안과 무니-리블린 고형물을 개발했다. 많은 다른 과대망상적 모델들이 그 이후로 개발되었다. 다른 널리 사용되는 과대망상 재료 모델로는 Ogden 모델과 Arruda-Boyce 모델이 있다.

과급성 재료 모델

세인트베난트-키르호프 모델

가장 단순한 과대망상 재료 모델은 기하학적 선형 탄성 재료 모델을 기하학적 비선형 체제로 확장한 Saint Venant-Kirchhoff 모델이다. 이 모델은 일반 형태와 등방성 형태를 각각 가진다.

${\displaystyle {\begin{aligned}{\boldsymbol {S}}&={\boldsymbol {C}}:{\boldsymbol {E}}\\{\boldsymbol {S}}&=\lambda ~{\text{tr}}({\boldsymbol {E}}){\boldsymbol {\mathit {I}}}+2\mu {\boldsymbol {E}}{\text{.}}}\end{정렬}}$

여기서${\displaystyle }$: ${\$은(는) 긴장 $수축$이고, S$${\$displaystyle {\boldsymbol{S}$은(는) 두 번째 Piola-Kirchhoff 스트레스$$,${\displaystyle }C{\displaystyle \mathit{}}$ : ${\displaystyle {I\mathrm{}}^{}}$ : ${\displaystyle 3^{\mathrm{}}{\times }^{}}$ 3 →${\displaystyle {}^{}{\mathrm{I}}^{}}$ ${\displaystyle {\mathrm{}}^{}}$ ${\displaystym$ {$I}!$$R}}^{3\time 3}\오른쪽 화살표 {\rm {I\!$$R}^{3\times$ 3$.}$는 네 번째 순서 강성 텐서이고 E ${\$은(는) 다음과 같은 라그랑지안 그린 변형률이다.

${\displaystyle \mathbf {E} ={\frac {1}{2}}\left[(\nabla _{\mathbf {X} }\mathbf {u} )^{\textsf {T}}+\nabla _{\mathbf {X} }\mathbf {u} +(\nabla _{\mathbf {X} }\mathbf {u} )^{\textsf {T}}\cdot \nabla _{\mathbf {X} }\mathbf {u} \right]\,\!}$

${\displaystyle \lambda }$ ${\displaystyle \lambda },$ $\mu s{\displaystyle }$ ${\displaystyle \mu }$이(가) 라메 상수이며, $I{\displaystyle \mathit{}}$ ${\$이(가)가$$ 두 번째 순서 단위 텐서이다.

Saint Venant-Kirchhoff 모델의 변형 에너지 밀도 함수는

${\displaystyle W({\boldsymbol{E}})={\frac {\lambda }{{\boldsymbol{E}}}}^{2}+\mu{\text{tr}}{\mathord{\\\\\boldsymbol {E}}\오른쪽)}}}$

그리고 두 번째 피올라-키르호프 스트레스는 관계에서 파생될 수 있다.

${\displaystyle {\boldsymbol{S}={\cfrac {\partial W}{\partial {\\boldsymbol{E}}}}.}$

과대성 재료 모델의 분류

과대성 재료 모델은 다음과 같이 분류할 수 있다.

1. 관찰된 행동에 대한 현상학적 묘사
   • 풍
   • 무니-리블린
   • 오그덴
   • 다항식
   • 세인트베낭키르호프
   • 예오
   • 말로우
2. 재료의 기초 구조에 관한 논쟁에서 도출된 기계론적 모델들
   • 아루다-보이스 모델^[5]
   • 네오후크 모델^[1]
   • 부체-실버슈타인 모델^[6]
3. 현상학적 모델과 기계론적 모델의 혼합물
   • 젠트
   • 반데르발스

일반적으로 과대망상 모델은 Drucker 안정성 기준을 충족해야 한다. ${\displaystyle {}_{}}$ 과급성 모델은 스트레인 에너지 함수를 주 스트레인 스트레인의 개별 함수의 ${\displaystyle {합}_{}}$으로 분리할 수 있다는 Valanis-Landel 가설을 ${\displaystyle {만족}_{}}$시킨다$(\lambda _{1},\lambda _{2},\lambda _{3$

${\displaystyle W=f(\lambda _{1})+f(\lambda _{2})+f(\lambda _{3}\,}$

스트레스-스트레인 관계

압축성 과급성 재료

첫 번째 피올라-키르호프 스트레스

$W{\displaystyle }$(${\displaystyle F\mathit{}}$) ${\displaystyle W({\boldsymbol{F}}})$가 변형 에너지 밀도 함수라면 과대성 물질에 대해 1번째 Piola-Kirchhoff 응력 텐서를 다음과 같이 계산할 수 있다.

${\displaystyle {\boldsymbol{P}={\frac {\partial W}{\partial {\boldsymbol{F}}}}}\partial {\qquad P_{iK}={\frac {\partial F_{iK}}}}}.}$

여기서 $F{\displaystyle \mathit{}}$ ${\$은(는) 변형 구배입니다. 라그랑지안 그린 변형률(${\displaystyle \mathit{}}$ ${\$의 관점에서 보면.

${\displaystyle {\boldsymbol {P}}={\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}\qquad {\text{or}}\qquad P_{iK}=F_{iL}~{\frac {\partial W}{\partial E_{LK}}}~.}$

오른쪽 Cauchy-Green 변형 텐서(${\displaystyle \mathit{}}$ ${\$의 측면

${\displaystyle {\boldsymbol {P}}=2~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}\qquad {\text{or}}\qquad P_{iK}=2~F_{iL}~{\frac {\partial W}{\partial C_{LK}}}~.}$

제2의 피올라-키르호프 스트레스

$S{\displaystyle \mathit{}}$ ${\$이(가) 두 번째 Piola-Kirchhoff 스트레스 텐서인 경우

${\displaystyle {\boldsymbol{S}={\boldsymbol{F}^{-1}\cdot {\frac {\partial W}{\partial {\partial {\\poldsymbol{F}}}\qquad{\\text}}\qquad S_{{{{{{{{{{}}}}}}}}}}IJ}=F_{Ik}^{-1}{\frac {\partial W}{\partial F_{kJ}}~}$

라그랑지안 그린 스트레인 면에서는

${\displaystyle {\boldsymbol {S}={\frac {\partial W}{\partial {\boldsymbol{E}}}\partial {\boldsymbol}}\cult{or}\cext}\qquad S_{{{{{{}}}}}}}}IJ}={\frac {\partial W}{\partial E_{IJ}}~.}$

오른쪽 Cauchy-Green 변형 텐서 측면에서

${\displaystyle {\boldsymbol {S}=2~{\frac {\partial W}{\partial {C}}}\partial {\boldsymbol}}}}}\partial S_{{IJ}=2~{\frac {\partial W}{partial C_{{{{{}}}}}}}}}}IJ}}~.}$

위의 관계는 재료 구성에서 도일-에릭센 공식으로도 알려져 있다.

코치 스트레스

이와 유사하게, 코치 스트레스는 다음에 의해 주어진다.

${\displaystyle {\boldsymbol {\sigma }}={\cfrac {1}{J}}~{\cfrac {\partial W}{\partial {\boldsymbol {F}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}~;~~J:=\det {\boldsymbol {F}}\qquad {\text{or}}\qquad \sigma _{ij}={\cfrac {1}{J}}~{\cfrac {\partial W}{\partial F_{iK}}}~F_{jK}~.}$

라그랑지안 그린 스트레인 면에서는

${\displaystyle {\boldsymbol {\sigma }}={\cfrac {1}{J}}~{\boldsymbol {F}}\cdot {\cfrac {\partial W}{\partial {\boldsymbol {E}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}\qquad {\text{or}}\qquad \sigma _{ij}={\cfrac {1}{J}}~F_{iK}~{\cfrac {\partial W}{\partial E_{KL}}}~F_{jL}~.}$

오른쪽 Cauchy-Green 변형 텐서 측면에서

${\displaystyle {\boldsymbol {\sigma }}={\cfrac {2}{J}}~{\boldsymbol {F}}\cdot {\cfrac {\partial W}{\partial {\boldsymbol {C}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}\qquad {\text{or}}\qquad \sigma _{ij}={\cfrac {2}{J}}~F_{iK}~{\cfrac {\partial W}{\partial C_{KL}}}~F_{jL}~.}$

위의 표현은 비등방성 매체에도 유효하다(이 경우, 잠재적 함수는 초기 섬유 방향과 같은 기준 방향 양에 암묵적으로 의존하는 것으로 이해된다). 동위원소의 특별한 경우, Cauchy 응력은 다음과 같이 왼쪽 Cauchy-Green 변형 텐서 단위로 표현할 수 있다.^[7]

${\displaystyle {\boldsymbol {\sigma }}={\cfrac {2}{J}}~{\boldsymbol {B}}\cdot {\cfrac {\partial W}{\partial {\boldsymbol {B}}}}\qquad {\text{or}}\qquad \sigma _{ij}={\cfrac {2}{J}}~B_{ik}~{\cfrac {\partial W}{\partial B_{kj}}}~.}$

비압축성 과극성 소재

압축할 수 없는 $재료$의 경우 J ${\displaystyle :=det\mathrm{F}}$ = 1 ${\displaystyle J:=\det${\$boldsymbol{F}=1$ 따라서 비압축성 제약조건은 ${\displaystyle \mathrm{J}}$- ${\displaystyle 1}$= 0 ${\displaystyle J-1=0}$ 입니다$.$ 과극성 물질의 압축성을 보장하기 위해 변형 에너지 함수는 다음과 같은 형태로 작성할 수 있다.

${\displaystyle W=W({\boldsymbol{F}})-p~(J-1)}$

여기서 정수압 $p{\displaystyle }$ ${\displaystyle p}$은(는) 라그랑의 승수로서 불압력$$ 구속조건을 시행한다. 제1회 피올라-키르호프 스트레스는 이제 더욱 강해진다.

${\displaystyle {\boldsymbol {P}}=-p~J{\boldsymbol {F}}^{-{\textsf {T}}}+{\frac {\partial W}{\partial {\boldsymbol {F}}}}=-p~{\boldsymbol {F}}^{-{\textsf {T}}}+{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}=-p~{\boldsymbol {F}}^{-{\textsf {T}}}+2~{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {C}}}}~.}$

이 응력 텐서는 이후 다음과 같은 다른 전통적인 스트레스 텐서로 변환될 수 있다. 예를 들어, Cauchy 스트레스 텐서는 다음과 같다.

${\displaystyle {\boldsymbol {\sigma }}={\boldsymbol {P}}\cdot {\boldsymbol {F}}^{\textsf {T}}=-p~{\boldsymbol {\mathit {1}}}+{\frac {\partial W}{\partial {\boldsymbol {F}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}=-p~{\boldsymbol {\mathit {1}}}+{\boldsymbol {F}}\cdot {\frac {\partial W}{\partial {\boldsymbol {E}}}}\cdot {\boldsymbol {F}}^{\textsf {T}}=-p~{\boldsymbol {\mathit {1}+2~{\boldsymbol {F}\partial W}{\partial {\\\boldsymbol{C}}}\cdot{\boldsymbol{F}^{\t}}}}.}$

Cauchy 응력 표현식

압축성 등방성 과급성 재료

등방성 과극성 재료의 경우, 코치 응력은 왼쪽 코치-녹색 변형 텐서(또는 오른쪽 코치-녹색 변형 텐서)의 불변성 측면으로 표현할 수 있다. If the strain energy density function is ${\displaystyle W({\boldsymbol {F}})={\hat {W}}(I_{1},I_{2},I_{3})={\bar {W}}({\bar {I}}_{1},{\bar {I}}_{2},J)={\tilde {W}}(\lambda _{1},\lambda _{2},$$\lambda _{3$ 그러면

${\displaystyle {\begin{aigned}{\boldsymbol {\sigma }}&={\cfrac {2}{{I_{3}}}}\prefrac {\partial {W}{1}+}I_{1}~{\cfrac{\partial{\hat{W}}}{\partial I_{2}}}\right){\boldsymbol{B}}-{\cfrac{\partial{\hat{W}}}{\partial I_{2}}}~{\boldsymbol{B}}\cdot{\boldsymbol{B}}\right]+2{\sqrt{I_{3}}}~{\cfrac{\partial{\hat{W}}}{\partial I_{3}}}~{\boldsymbol{\mathit{1}}}\\[5pt]&, ={\cfrac{2}{J}}\left는 경우에는{\cfrac{1}{J^{2/3}}}\left({\cfrac{\partial{\bar{W.}}}{\partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\cfrac {\partial {\bar {W}}}{\partial {\bar {I}}_{2}}}\right){\boldsymbol {B}}-{\cfrac {1}{J^{4/3}}}~{\cfrac {\partial {\bar {W}}}{\partial {\bar {I}}_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+\left[{\cfrac {\partial {\bar {W}}}{\partial J}}-{\cfrac {2}{3J}}\left({\bar{나는}}_{1}일{\cfrac{\partial{\bar{W}}}{{\bar{나는}}_{1}}}+2~{\bar{나는}}_{2}일{\cfrac{\partial{\bar{W}}}{\partial{\bar{나는}}_{2}}}\partial \right)\right 해결 ~{\boldsymbol{\mathit{1}}}\\[5pt]&, ={\cfrac{2}{J}}\left는 경우에는 \left({\cfrac{\partial{\bar{W}}}{\partial{\bar{나는}}_{1}}}+{\bar{나는}}_{1}~{\cfrac{\partial{\bar{W}}}{\partial{\bar. {나는}}_{2}}}\right){\bar {\boldsymbol {B}}}-{\cfrac {\partial {\bar {W}}}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]+\left[{\cfrac {\partial {\bar {W}}}{\partial J}}-{\cfrac {2}{3J}}\left({\bar{나는}}_{1}일{\cfrac{\partial{\bar{W}}}{{\bar{나는}}_{1}}}+2~{\bar{나는}}_{2}일{\cfrac{\partial{\bar{W}}}{\partial{\bar{나는}}_{2}}}\partial \right)\right 해결 ~{\boldsymbol{\mathit{1}}}\\[5pt]&, ={\cfrac{\lambda_{1}}{\lambda_{1}\lambda _{2}\lambda _{3}}}~{\cfrac{\partial{\tilde{W}}}{\partial \lambda_{1}}}){n}_{1}\otimes ~\mathbf.수학bf {n} _{1}+{\cfrac {\lambda _{2}}{\lambda _{1}\lambda _{2}\lambda _{3}}}~{\cfrac {\partial {\tilde {W}}}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+{\cfrac {\lambda _{3}}{\lambda _{1}\lambda _{2}\lambda _{3}}}~{\cfrac {\partial {\tilde {W}}}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\end{aligned}}}$

(이 기호의 정의는 왼쪽 Cauchy-Green 변형 텐서 페이지를 참조하십시오.)

증명 1:

과대성 물질에 대한 두 번째 Piola-Kirchhoff 응력 텐서는 다음과 같다. ${\displaystyle {\boldsymbol{S}=2~{\cfrac {\partial W}{\partial {\boldsymbol{C}}}}}$ 여기서 $C{\displaystyle \mathit{}}$= ${\displaystyle {\mathit{}}^{}}$ ${\displaystyle {}^{}}$⋅ ${\displaystyle F\mathit{}}$ ${\boldsymbol {C}={\boldsymbol {F}^{T}\cdot{\boldsymbol$ {$F}}}$은(는) 오른쪽 Cauchy–Green 변형 텐서이고 $F{\displaystyle \mathit{}}$ ${\$은 변형 그라데이션이다. 카우치 스트레스는 에 의해 주어진다. ${\displaystyle {\boldsymbol {\sigma}}={\cfrac {1}{{J}}~{\boldsymbol {F}\boldsymbol {S}\boldsymbol {F}^{\boldsymbol}}}^{{{}}}}}}}}}}}}}}}{T}={\cfrac{2}{J}~{\boldsymbol{F}\cdot{\cdoc{\partial W}{\partial {\boldsymbol{C}}}\cdot{\boldsymbol{F}}^{}}}}}{\\boldsymb}}}}}}}}}}}}}}}}}}^{T}$ 여기서 $J{\displaystyle }$= ${\displaystyle det}$ ${\displaystyle F\mathit{}}$ ${\$ $I{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$, I ${\displaystyle {3\mathrm{}}_{}}$ ${\$은(는$)$ C {\$displaystyle {\\boldmbol{C}$의 세 가지 주요 불변수이다$.$ ${\displaystyle {\cfrac {\partial W}{\partial {\boldsymbol {C}}}}={\cfrac {\partial W}{\partial I_{1}}}~{\cfrac {\partial I_{1}}{\partial {\boldsymbol {C}}}}+{\cfrac {\partial W}{\partial I_{2}}}~{\cfrac {\partial I_{2}}{\partial {\boldsymbol {C}}}}+{\cfrac {\partial W}{\partial I_{3}}}~{\cfrac {\partial I_{3}}{\partial {\boldsymbol {C}}}}~.}$ 대칭 텐서 $C{\displaystyle \mathit{}}$ ${\$의 불변성분들의 파생상품은 다음과$$ 같다. ${\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {C}}}}={\boldsymbol {\mathit {1}}}~;~~{\frac {\partial I_{2}}{\partial {\boldsymbol {C}}}}=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {C}}~;~~{\frac {\partial I_{3}}{\partial {\boldsymbol {C}}}}=\det({\boldsymbol {C}})~{\boldsymbol {C}}^{-1}}$ 그러므로 우리는 글을 쓸 수 있다. ${\displaystyle {\cfrac {\partial W}{\partial {\boldsymbol {C}}}}={\cfrac {\partial W}{\partial I_{1}}}~{\boldsymbol {\mathit {1}}}+{\cfrac {\partial W}{\partial I_{2}}}~(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}})+{\cfrac {\partial W}{\partial I_{3}}}~I_{3}~{\boldsymbol {F}^{-1}\cdot {\boldsymbol{F}^{-T}}$ Cauchy 스트레스에 대한 표현에 연결하면 ${\displaystyle {\boldsymbol {\sigma }}={\cfrac {2}{J}}~\left[{\cfrac {\partial W}{\partial I_{1}}}~{\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}+{\cfrac {\partial W}{\partial I_{2}}}~(I_{1}~{\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}-{\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}\cdot {\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T})+{\cfrac {\partial W}{\partial I_{3}}~I_{3}~{\boldsymbol {\mathit {1}\오른쪽]}$ Using the left Cauchy–Green deformation tensor ${\displaystyle {\boldsymbol {B}}={\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}}$ and noting that ${\displaystyle I_{3}=J^{2}}$, we can write ${\displaystyle {\boldsymbol {\sigma }}={\cfrac {2}{\sqrt{I_{3}}}}}\왼쪽({\cfrac {\partial W}{\partial I_{1}}}}}}}}+I_{1}~{\cfrac {\partial W}{\partial I_{2}}}\right)~{\boldsymbol {B}}-{\cfrac {\partial W}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+2~{\sqrt {I_{3}}}~{\cfrac {\partial W}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}~.}$ 압축할 수 $없는{\displaystyle {}_{}}$ ${\displaystyle {재료\mathrm{}}_{}}$I ${\displaystyle 3}$ =$$1 {\$displaystyle I_{$3$$$}=1$} 및${\displaystyle }따라서{\displaystyle }$ ${\displaystyle W}$ = W${\displaystyle ({I\mathrm{}}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}}$I${\displaystyle {}_{}}$2$$) {\$displaystyle$ W$=W(I_{1},I_{$2$\}\}\}\}.$그러면 ${\displaystyle {\cfrac {\partial W}{\partial {\boldsymbol {C}}}}={\cfrac {\partial W}{\partial I_{1}}}~{\cfrac {\partial I_{1}}{\partial {\boldsymbol {C}}}}+{\cfrac {\partial W}{\partial I_{2}}}~{\cfrac {\partial I_{2}}{\partial {\boldsymbol {C}}}}={\cfrac {\partial W}{\partial I_{1}}}~{\boldsymbol {\mathit {1}}}+{\cfrac {\partial W}{\partial I_{2}}}}}(I_{1}~{\boldsymbol {1}-{\boldsymbol {1}-{\boldsymbol{F}^{T}\cdot{\boldsymbol {F})}}}}$ 그러므로 코치 스트레스는 다음과 같이 주어진다. ${\displaystyle {\boldsymbol {\sigma }}=2\왼쪽[{\cfrac {\partial W}{\partial I_{1}}}+I_{1}~{\cfrac {\partial W}{\partial I_{2}}}\right)~{\boldsymbol {B}}-{\cfrac {\partial W}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]-p~{\boldsymbol {\mathit {1}}}~.}$ 여기서 $p{\displaystyle }$ ${\displaystyle p}$은(는) 불압력 제약 조건을 시행하는 라그랑주 승수 역할을 하는 결정되지 않은 압력이다$$. ${\displaystyle {I\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$인 경우$I_{2$ $W{\displaystyle }$= ${\displaystyle W}$( ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$) ${\displaystyle W=W(I_{1}})$가 있으므로 ${\displaystyle {\cfrac {\partial W}{\partial {\boldsymbol {C}}}}={\cfrac {\partial W}{\partial I_{1}}}~{\cfrac {\partial I_{1}}{\partial {\boldsymbol {C}}}}={\cfrac {\partial W}{\partial I_{1}}}~{\boldsymbol {\mathit {1}}}}$ 그 경우 코치 스트레스는 다음과 같이 표현할 수 있다. ${\displaystyle {\boldsymbol {\sigma }=2{\cfrac {\partial I_{1}}~{\boldsymbol{B}-p~{\boldsymbol{\mathit{1}.}$

증명 2:

등축 변형 구배는 $F{\displaystyle \stackrel{}{\mathit{}}}$ -${\displaystyle 1^{}}$/ ${\displaystyle {}^{}\mathit{}}$ F ${\$로 정의되며$,$ 따라서 1의 결정 인자를 갖는 등축 변형 구배는 볼륨이 없는 것이다. Using this one can subsequently define the isochoric left Cauchy–Green deformation tensor ${\displaystyle {\bar {\boldsymbol {B}}}:={\bar {\boldsymbol {F}}}\cdot {\bar {\boldsymbol {F}}}^{T}=J^{-2/3}{\boldsymbol {B}}}$. The invariants of ${\displaystyle {\bar {\boldsymbol {B}}}}$ are ${\displaystyle {\begin{aligned}{\bar {I}}_{1}&={\text{tr}}({\bar {\boldsymbol {B}}})=J^{-2/3}{\text{tr}}({\boldsymbol {B}})=J^{-2/3}$$I_{1}\\{\bar {I}}_{2}&={\frac {1}{2}}\left({\text{tr}}({\bar {\boldsymbol {B}}})^{2}-{\text{tr}}({\bar {\boldsymbol {B}}}^{2})\right)={\frac {1}{2}}\left(\left(J^{-2/3}{\text{tr}}({\boldsymbol {B}})\right)^{2}-{\text{tr}}(J^{-4/3}{\boldsymbol {B}}^{2})\right)=$$J^{-4/3}$$I_{2}\\\bar {I}_{3}&=\det({\bar {\boldsymbol{B}}}}}=J^{-6/3}\det({\boldsymbol {B}})=J^{-2}$$I_{3}=J^{-2}J^{2}=1\end{aligned}}}$ The set of invariants which are used to define the distortional behavior are the first two invariants of the isochoric left Cauchy–Green deformation tensor tensor, (which are identical to the ones for the right Cauchy Green stretch tensor), and add ${\displaystyle J}$ into the fray to describe the volume진부한 행동 카우치 스트레스를 불변제 $I{\displaystyle {\stackrel{}{}}_{}{1}_{\mathrm{}}}$, ${\displaystyle I{\stackrel{}{\text{'}\text{'}}2}_{\mathrm{}}}$,${\displaystyle {}_{}}$J ${\displaystyle {\bar{I}_{1},{\bar {I}_{2},J}$가 상기한다. ${\displaystyle {\bar{I}_{1}=J^{-2/3}~~I_{1}=I_{3}^{-1/3}~~I_{1}~;~{\bar{I}_{2}=J^{-4/3}~~I_{2}=I_{3}^{-2/3}~~I_{2}~;~J=I_{3}^{1/2}.}$ 차별화의 연쇄 법칙은 우리에게 ${\displaystyle {\begin{aligned}{\cfrac {\partial W}{\partial I_{1}}}&={\cfrac {\partial W}{\partial {\bar {I}}_{1}}}~{\cfrac {\partial {\bar {I}}_{1}}{\partial I_{1}}}+{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}~{\cfrac {\partial {\bar {I}}_{2}}{\partial I_{1}}}+{\cfrac {\partial W}{\partial J}}~{\cfrac {\partial J}{\partial I_{1}}}\\&=I_{3}^{-1/3}~{\cfrac{\partial W}{\partial{\bar{나는}}_{1}}}=J^{-2/3}~{\cfrac{\partial W}{\partial{\bar{나는}}_{1}}}\\{\cfrac{\partial W}{\partial I_{2}}}&={\cfrac{\partial W}{\partial{\bar{나는}}_{1}}}~{\cfrac{\partial{\bar{나는}}_{1}}{\partial I_{2}}}+{\cfrac{\partial W}{\partial{\bar{나는}}_{2}}}~{\cfrac{\partial{\bar{나는}}_{2}}{\partial I_.{2}}}}+{\cfrac {\partial W}{\partial J}~{\cfrac {\partial J}{\partial I_{2}}}\&=I_{3}^{-2/3}~{\cfrac{\partial W}{\partial{\bar{나는}}_{2}}}=J^{-4/3}~{\cfrac{\partial W}{\partial{\bar{나는}}_{2}}}\\{\cfrac{\partial W}{\partial I_{3}}}&={\cfrac{\partial W}{\partial{\bar{나는}}_{1}}}~{\cfrac{\partial{\bar{나는}}_{1}}{\partial I_{3}}}+{\cfrac{\partial W}{\partial{\bar{나는}}_{2}}}~{\cfrac{\partial{\bar{나는}}_{2}}{\partial I_.{3}}}}+{\cfrac {\partial W}{\partial J}~{\cfrac {\partial J}{\partial I_{3}}\&=-{\cfrac {1}{3}}}}~I_{3}^{-4/3}~~I_{1}~{\cfrac {\partial W}{\partial {\bar{I}_{1}}-{\cfrac {2}{3}}}~I_{3}^{-5/3}~~I_{2}~{\cfrac {\partial W}{\partial {\bar{I}_{2}}+{\cfrac {1}{1}2}}~I_{3}^{-1/2}~{\cfrac{\partial W}{J\partial}}\\&, =-{\cfrac{1}{3}}~J^{-8/3}~J^{2/3}~{\bar{나는}}_{1}~{\cfrac{\partial W}{\partial{\bar{나는}}_{1}}}-{\cfrac{2}{3}}~J^{-10/3}~J^{4/3}~{\bar{나는}}_{2}~{\cfrac{\partial W}{\partial{\bar{나는}}_{2}}}+{\cfrac{1}{2}}~J^{)}~{\cfrac{\partial W}{J\partial}}\\&, =-{\cfrac{1}{3}}~J^{-2}~\left({\bar{나는}}._{1}~{\cfrac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}\right)+{\cfrac {1}{2}}~J^{-1}~{\cfrac {\partial W}{\partial J}}\end{aligned}}}$ Cauchy 스트레스는 다음에 의해 주어진다는 것을 상기하라. ${\displaystyle {\boldsymbol {\sigma }}={\cfrac {2}{\sqrt{I_{3}}}}}\왼쪽({\cfrac {\partial W}{\partial I_{1}}}}}}}}+I_{1}~{\cfrac {\partial W}{\partial I_{2}}}\right)~{\boldsymbol {B}}-{\cfrac {\partial W}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+2~{\sqrt {I_{3}}}~{\cfrac {\partial W}{\partial I_{3}}}~{\boldsymbol {\mathit {1}}}~.}$ 불변제 $I{\displaystyle {\stackrel{\text{'}}{}1}_{\mathrm{}}}$,${\displaystyle {}_{}{\stackrel{\text{'}\text{'}}{}}_{}2}$,${\displaystyle {}_{}}$J ${\displaystyle {\bar{I}_{1},{\bar {I}_{2},J}$이(가) 있다. ${\displaystyle {\boldsymbol {\sigma }}={\cfrac {2}{J}}~\left[\left({\cfrac {\partial W}{\partial I_{1}}}+J^{2/3}~{\bar {I}}_{1}~{\cfrac {\partial W}{\partial I_{2}}}\right)~{\boldsymbol {B}}-{\cfrac {\partial W}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+2~J~{\cfrac {\partial W}{\partial I_{3}}~{\boldsymbol {\mathit{1}}.}$ ${\displaystyle W_{\mathrm{}}}$ ${\displaystyle W}$의 파생상품에 대한 표현을$$ I${\displaystyle {}_{}}$1, ${\displaystyle I{\stackrel{}{\text{'}}2}_{\mathrm{}}}$,${\displaystyle {}_{}}$J ${\displaystyle {\bar{I}_{1},{\bar {I}_{2}, J$와 같이 입력하십시오. ${\displaystyle{\begin{정렬}{\boldsymbol{\sigma}}&={\cfrac{2}{J}}~\left[\left(J^{-2/3}일{\cfrac{\partial W}{\partial{\bar{나는}}_{1}}}+J^{-2/3}일{\bar{나는}}_{1}일{\cfrac{\partial W}{\partial{\bar{나는}}_{2}}}\right)~{\boldsymbol{B}}-J^{-4/3}일{\cfrac{\partial W}{{\bar{나는}\partial}_{2}}}일{\boldsymbol{B}}\cdot{\boldsymbol{B}}\right]+\\&.;\qquad 2~J~\left[-{\cfrac {1}{3}}~J^{-2}~\left({\bar {I}}_{1}~{\cfrac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}\right)+{\cfrac {1}{2}}~J^{-1}~{\cfrac {\partial W}{\partial J}}\right]~{\boldsymbol {\mathit {1}}}\end{aligned}}}$ 또는 ${\displaystyle{\begin{정렬}{\boldsymbol{\sigma}}&={\cfrac{2}{J}}~\left는 경우에는{\cfrac{1}{J^{2/3}}}~\left({\cfrac{\partial W}{\partial{\bar{나는}}_{1}}}와{\bar{나는}}_{1}일{\cfrac{\partial W}{\partial{\bar{나는}}_{2}}}\right)~{\boldsymbol{B}}-{\cfrac{1}{J^{4/3}}}~{\cfrac{\partial W}{\partial{\bar{나는}}_{2}}}~{\boldsymbol{B}}\cdot{\boldsymbol{.B}})오른쪽]\\\&\qquad +\왼쪽[{\cfrac {\partial W}{\partial J}-{\cfrac {2}{3]J}}\left({\bar {I}}_{1}~{\cfrac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}\right)\right]{\boldsymbol {\mathit {1}}}\end{aligned}}}$ $B{\displaystyle \mathit{}}$ ${\$의 Deviatoric 부분에 대해서는, 우리는 쓸 수 있다$.$ ${\displaystyle {\begin{aligned}{\boldsymbol {\sigma }}&={\cfrac {2}{J}}~\left[\left({\cfrac {\partial W}{\partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}\right)~{\bar {\boldsymbol {B}}}-{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]\\&\qquad +\왼쪽[{\cfrac {\partial W}{\partial J}-{\cfrac {2}{3]J}}\left({\bar {I}}_{1}~{\cfrac {\partial W}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}\right)\right]{\boldsymbol {\mathit {1}}}\end{aligned}}}$ 비압축성${\displaystyle }재료{\displaystyle }$ ${\displaystyle \mathrm{J}}$ =$$1 {\$displaystyle$ J$=1},$ $따라서$ ${\displaystyle W}$= W${\displaystyle ({\stackrel{\text{'}\text{'}}{}1}_{\mathrm{}}}$,${\displaystyle {}_{}{\stackrel{\text{'}\text{'}}{}2}_{\mathrm{}}}$) ${\displaystyle W=W({\bar {I}_{1},{\bar {I}_{2$그러면 코치 스트레스는 에 의해 주어진다. ${\displaystyle {\boldsymbol {\sigma}}=2\왼쪽[{\cfrac {\partial W}{\partial W}{\partial {\bar{I}_{1}}}+I_{1}~{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}\right)~{\bar {\boldsymbol {B}}}-{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]-p~{\boldsymbol {\mathit {1}}}~.}$ 여기서 $p{\displaystyle }$ ${\displaystyle p}$은(는) 결정되지 않은 압력형 라그랑주 승수 용어다$$. 덧붙여 ${\displaystyle I_{\mathrm{}}{\stackrel{}{}}_{}}$`1$`{\$${\displaystyle }$W${\displaystyle }$= ${\displaystyle W}$ ($}}{\displaysty$ W$=W({\bar{I}_{1$}})가$$ 있으면$,$ Cauchy 스트레스는 그대로 표현될 수 있다. ${\displaystyle {\boldsymbol {\sigma}=2{\cfrac {\partial W}{\bar{I}_{1}:{\bar {\boldsymbol {B}-p~{\boldsymbol {1}-p~{\mathit{1}.}}$

증명 3:

카우치 스트레스를 스트레스의 ${\displaystyle {\lambda 1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle {}_{}{\lambda \mathrm{}}_{}}$ 3 ${\$의 스트레스로 표현하려면 다음을 상기하십시오$$. ${\displaystyle {\cfrac {\partial \lambda _{i}}{\partial {\boldsymbol {C}}}}={\cfrac {1}{2\lambda _{i}}}~{\boldsymbol {R}}^{T}\cdot (\mathbf {n} _{i}\otimes \mathbf {n} _{i})\cdot {\boldsymbol {R}}~;~~i=1,2,3~.}$ 그 사슬의 법칙은 다음과 같다. ${\displaystyle{\begin{정렬}{\cfrac{\partial W}{\partial{\boldsymbol{C}}}}&={\cfrac{\partial W}{\partial \lambda_{1}}}~{\cfrac{\partial \lambda_{1}}{\partial{\boldsymbol{C}}}}+{\cfrac{\partial W}{\partial \lambda_{2}}}~{\cfrac{\partial \lambda_{2}}{\partial{\boldsymbol{C}}}}+{\cfrac{\partial W}{\partial \lambda_{3}}}일{\cfrac.{\pArtial(_{3}}{\partial{\boldsymbol{C}}}}\\&, ={\boldsymbol{R}}^{T}\cdot\left[{\cfrac{1}{2\lambda_{1}}}~{\cfrac{\partial W}{\partial \lambda_{1}}}}}\mathbf{n}_{2}+{\cfrac{1}{2\lambda_{3}}}일{\cf{n}_{2}\otimes ~\mathbf{n}_{1}\otimes \mathbf{n}_{1}+{\cfrac{1}{2\lambda_{2}}}~{\cfrac{\partial W}{\partial \lambda_{2}~\mathbf.rac {\partial W}{\partial \lambda _{3}}~{3}\mathbf {n} _{3}\hright]\cdot {\boldsymbol {R}\ended}}}}}}}$ 카우치 스트레스는 에 의해 주어진다. ${\displaystyle {\boldsymbol {\sigma}}={\cfrac {2}{J}~{\boldsymbol {F}\cdot {\partial W}{\partial {\boldsymbol{C}}}}}\cdot {\\bmbol {F}^{{{F}^}}}}}}}}^T}={\cfrac {2}{J}}~({\boldsymbol {V}}\cdot {\boldsymbol {R}})\cdot {\cfrac {\partial W}{\partial {\boldsymbol {C}}}}\cdot ({\boldsymbol {R}}^{T}\cdot {\boldsymbol {V}})}$ $W{\displaystyle }$ ${\displaystyle W}$의 파생 모델에 대한 식을 연결하면$$ ${\displaystyle {\boldsymbol {\sigma }}={\cfrac {2}{J}}~{\boldsymbol {V}}\cdot \left[{\cfrac {1}{2\lambda _{1}}}~{\cfrac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+{\cfrac {1}{2\lambda _{2}}}~{\cfrac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+{\cfrac {1}{2\lambda _{3}}}~{\cfrac {\부분 W}{\partial \lambda _{3}}~~mathbf {n} _{3}\otimes \mathbf {n} _{3}\right]\cdot {\boldsymbol {V}}}}}$ $V$ ${\$의 스펙트럼 분해 사용 ${\displaystyle {\boldsymbol {V}}\cdot (\mathbf {n} _{i}\otimes \mathbf {n} _{i})\cdot {\boldsymbol {V}}=\lambda _{i}^{2}~\mathbf {n} _{i}\otimes \mathbf {n} _{i}~;~~i=1,2,3.}$ 또한 이 점에 유의하십시오. ${\displaystyle J=\det({\boldsymbol {F}})=\det({\boldsymbol {V}})=\det({\boldsymbol {V})=\lambda _{1}\lambda _{3}}}.$ 따라서 코우치 스트레스의 표현은 다음과 같이 쓸 수 있다. ${\displaystyle {\boldsymbol {\sigma }}={\cfrac {1}{\lambda _{1}\lambda _{2}\lambda _{3}}}~\left[\lambda _{1}~{\cfrac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda _{2}~{\cfrac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\lambda _{3}~{\cfrac {\partial W}{\partial \lambda _{3}}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\right]}$ For an incompressible material ${\displaystyle \lambda _{1}\lambda _{2}\lambda _{3}=1}$ and hence ${\displaystyle W=W(\lambda _{1},\lambda _{2})}$. Following Ogden[1] p. 485, we may write ${\displaystyle {\boldsymbol {\sigma }}=\lambda _{1}~{\cfrac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda _{2}~{\cfrac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\lambda _{3}~{\cfrac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}-p~{\boldsymbol {\mathit{1}}~}$ 고유값을 반복할 경우 일반적으로 Gateaux만 다를 수 있지만 Frechet은 다를 수 없기 때문에 이 단계에서 약간의 주의가 필요하다.[8][9] 엄격한 텐서 파생상품은 또 다른 고유가치 문제를 해결해야 찾을 수 있다. 만약 우리가 요소들 간의 차이점들의 관점에서 스트레스를 표현한다면, ${\displaystyle \sigma _{11}-\sigma _{33}=\lambda _{1}~{\cfrac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\cfrac {\partial W}{\partial \lambda _{3}}}~;~~\sigma _{22}-\sigma _{33}=\lambda _{2}~{\cfrac {\partial W}{\partial \lambda _{2}}}-\lambda _{3}~{\cfrac {\partial W}{\partial \lambda _{3}}}}$ 만일 우리가 ${\displaystyle {1\mathrm{}}_{}}$1 = ${\displaystyle {2\mathrm{}}_{}}$ 2$${\$displaystyle \lambda _{1}=\lambda _{2}}:$ 문제를$$ 해결할 수 있는 해결책은 $\sigma {\displaystyle {}_{}}$ ${\displaystyle {11}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle {22}_{}}$ ${\$이며 스트레스 차이를 다음과 같이 쓸 수 있다. ${\displaystyle \sigma _{11}-\sigma _{33}=\sigma _{22}-\sigma _{33}=\lambda _{1}~{\cfrac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\cfrac {\partial W}{\partial \lambda _{3}}}}$

비압축성 등방성 과대증상 물질

비압축성 등방성 과대배연성 물질의 경우 $변형{\displaystyle }$ 에너지 밀도 함수는 W${\displaystyle }$(${\displaystyle F\mathit{}}$)${\displaystyle }$= ${\displaystyle W\stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\displaystyle ({}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{I\mathrm{}}_{}}$ 2${\displaystyle {}_{}}$) ${\displaystyle$ W$({\boldsymbol$ {$F}})={\hat{W}(I_{1$},$I_{2$})이다$.$ 코치 스트레스는 그 다음 에 의해 주어진다.

${\displaystyle {\begin{aigned}{\boldsymbol {\sigma }}-p~{\boldsymbol {1}+2\\좌측[{\cfrac {\partial {\W}{\partial I_{1}}}}}+}+}+}+++++++++++++++++++++++++++++++++++++{\{\{\{\{\{\{\{\{\{I_{1}~{\cfrac {\partial {\hat {W}}}{\partial I_{2}}}\right){\boldsymbol {B}}-{\cfrac {\partial {\hat {W}}}{\partial I_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]\\&=-p~{\boldsymbol {\mathit {1}+2\왼쪽[{\cfrac {\partial W}{\partial W}{\partial {\bar{I}_{1}}}+I_{1}~{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}\right)~{\bar {\boldsymbol {B}}}-{\cfrac {\partial W}{\partial {\bar {I}}_{2}}}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}\right]\\&=-p~{\boldsymbol {\mathit {1}}}+\lambda _{1}~{\cfrac {\partial W}{\partial \lambda _{1}}}~\mathbf {n} _{1}\otimes \mathbf {n} _{1}+\lambda _{2}~{\cfrac {\partial W}{\partial \lambda _{2}}}~\mathbf {n} _{2}\otimes \mathbf {n} _{2}+\lambda _{3}~{\cfrac {\partial W}{\partial \lambda _{3}}}~\mathbf {n} _{3}\otimes \mathbf {n} _{3}\end{aligned}}}$

여기서 $p{\displaystyle }$ ${\displaystyle p}$은(는) 결정되지 않은 압력이다. 스트레스 차이 측면에서

${\displaystyle \sigma _{11}-\sigma _{33}=\lambda _{1}~{\cfrac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\cfrac {\partial W}{\partial \lambda _{3}}}~;~~\sigma _{22}-\sigma _{33}=\lambda _{2}~{\cfrac {\partial W}{\partial \lambda _{2}}}-\lambda _{3}~{\cfrac {\partial W}{\partial \lambda _{3}}}}$

$추가{\displaystyle {}_{}}$ ${\displaystyle {I\mathrm{}}_{}}$1 = ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$$I_{1}:{$2$\}\}:$ 그러면

${\displaystyle {\boldsymbol {\sigma }=2{\cfrac {\partial I_{1}}~{\boldsymbol{B}-p~{\boldsymbol{\mathit{1}.}$

$\lambda {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}인 경우$,$

${\displaystyle \sigma _{11}-\sigma _{33}=\sigma _{22}-\sigma _{33}=\lambda _{1}~{\cfrac {\partial W}{\partial \lambda _{1}}}-\lambda _{3}~{\cfrac {\partial W}{\partial \lambda _{3}}}}$

선형탄성과의 일관성

선형 탄성과의 일관성은 종종 과대성 재료 모델의 일부 매개변수를 결정하기 위해 사용된다. 이러한 일관성 조건은 작은 변종에서 Hoke의 법칙과 선형화된 과급성과의 비교를 통해 찾을 수 있다.

등방성 과속탄성 모델의 일관성 조건

등방성 과극성 재료가 등방성 선형 탄성과 일치하려면 응력-변형 관계는 최소 변형률 한계에서 다음과 같은 형태를 가져야 한다.

${\displaystyle {\basymbol {\basymbol {\barempsilon }{\\mathmbol {1}{1}+2\mu {\basymbol {\barepsilon}}}}}{\displaystymbol {\}}}}}$

여기서 $\mu {\displaystyle ,}$ $[\displaystyle \lambda ,\mu }$은(는) 라메 상수다. 위의 관계에 해당하는 변형 에너지 밀도 함수는^[1]

${\displaystyle W={\tfrac {1}{1}:{2}}\lambda ~[\mathrm {tr}({\boldsymbol {\barepsilon }}})^{2}+\mu ~\mathrm {tr} {\mathord {\\\\\\\\\\boldmbcol {}{}{}{}{}{}}}{{}오른쪽)}}}$

압축할 수 $없는{\displaystyle \mathrm{}}$ ${\displaystyle 재료\mathit{}}$ t r (${\displaystyle =}$ ) =$$ {\$displaystyle \mathrm${tr$}({\boldsymbol {\barepsilon }}})=0}$의 경우$$,

${\displaystyle W=\mu ~\mathrm {tr} {\mathord {\\왼쪽({\boldsymbol {\varepsilon }}}^{2}\오른쪽)}}}$

변형률 에너지 밀도 함수 $W{\displaystyle }$( ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle {}_{}{}_{}}$ ${\displaystyle {3\mathrm{}}_{}}$) ${\displaystyle W(\lambda _{1},\lambda _{2},\lambda _{3}})$를 작은 변형률에 대해 위의 형태로 줄이기 위해 다음과 같은 조건을 충족해야^[1] 한다.

${\displaystyle {\begin{aigned}&w(1,1,1)=0~~~~{\cfrac {\partial W}{\partial \lambda_{i}}(1,11)=0\&#\cfrac {\partial ^{2}W}{{\partial \lambda _{i}\partial \lambda _{j}}(1,1,1)=\lambda +2\mu \delta _{ij}\ended}}}}}}}$

재료가 압축할 수 없는 경우, 위의 조건은 다음과 같은 형태로 표현될 수 있다.

${\displaystyle {\begin{aligned}&W(1,1,1)=0\\&{\cfrac {\partial W}{\partial \lambda _{i}}}(1,1,1)={\cfrac {\partial W}{\partial \lambda _{j}}}(1,1,1)~;~~{\cfrac {\partial ^{2}W}{\partial \lambda _{i}^{2}}(1,1,1)={\cfrac {\partial ^{2}W}{\partial \lambda _{j}^{2}}(1,1,1)\\\cfrac {\partial ^{2}W}{{\partial \lambda _{i}\partial \lambda _{j}}(1,1,1)=\mathrm {독립형} ~i,j\neq i\\&}\cfrac {\partial ^{2}W}{\partial \lambda _{i}^{2}}(1,1,1)-{\cfrac {\partial ^{2}W}{{\partial \lambda _{i}\partial \lambda _{j}}+{\cfrac {\partial W}{\partial \lambda _{i}}}{partial \lambda _=2\mu~(i\neq j)\liged}}}}}}}}}}}}}}).$

이러한 조건은 주어진 과대망상 모델의 매개변수와 전단 및 벌크 모듈리 사이의 관계를 찾는 데 사용될 수 있다.

고무 재질 기반$$ ${\displaystyle {불압력\mathrm{}}_{}}$I 1 {\displaystyle $I_{1$}에 대한 일관성 조건

$많은$ 엘라스토머는 $1$에만 의존하는 변형 에너지 밀도 함수에 의해 적절하게 모델링된다$.$ 그러한 재료에는 $W{\displaystyle }$= ${\displaystyle W}$ (${\displaystyle }$I ${\displaystyle {1\mathrm{}}_{}}$ $){\displaystyle W=W(I_{1})$가 있다$.$ $I{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$= ${\displaystyle 3}$,${\displaystyle {\lambda }_{}}$ i${\displaystyle {}_{}}$= ${\displaystyle {\lambda }_{}}$ j${\displaystyle {}_{}}$= ${\displaystyle 1}$ ${\displaystyle I_{1}=3,\lambda _{i}=\lambda _{j}=1}$에 대한 압축불가 재료의 일관성 조건은 다음과 같이 나타낼$$ 수 있다.

$왼쪽.W(I_{1})\right _{I_{1}=3}=0\quad {\text{and}}\quad \왼쪽.{\cfrac {\partial W}{\partial I_{1}}}\right _{I_{1}=3}={\frac {\mu{2}}\,}$

위의 두 번째 일관성 조건은 다음 사항을 참고하여 도출할 수 있다.

${\displaystyle {\cfrac {\partial W}{\partial \lambda _{i}}}={\cfrac {\partial W}{\partial I_{1}}}{\cfrac {\partial I_{1}}{\partial \lambda _{i}}}=2\lambda _{i}{\cfrac {\partial W}{\partial I_{1}}}\quad {\text{and}}\quad {\cfrac {\partial ^{2}W}{{\partial \lambda _{i}\partial \lambda _{j}}=2\delta _{ij}{\partial I_{1}}+4+lambda _{i}{j}{\cfr}{partial ^{n2}W}{\partial I_{1}^{2}}\,}$

그런 다음 이러한 관계는 등방성 비압축성 과극성 물질의 일관성 조건으로 대체될 수 있다.

참조

참고 항목

• 코시 탄성 소재
• 연속체 역학
• 변형(기전)
• 유한변형 이론
• 오그덴-록스버그 모델
• 고무탄성
• 응력 측정
• 응력(기)