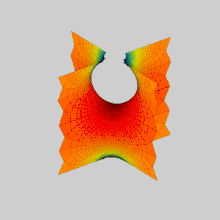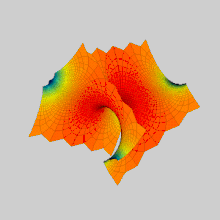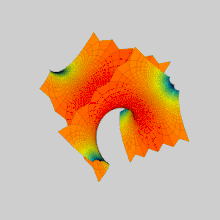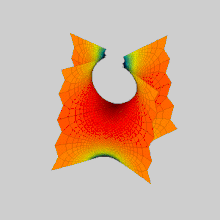
스크허크면

수학에서 스허크 표면(하인리히 스허크의 이름을 딴 이름)은 최소한의 표면의 예다.Scherk은 1834년에 두 개의 완전한 삽입된 최소 표면을 묘사했다; 그의 첫 표면은 두 배로 주기적인 표면이고, 두 번째 표면은 단일 주기적인 표면이다.^[1]그것들은 최소 표면의 세 번째 비경쟁적 예였다(첫 번째 두 가지는 카티노이드와 헬리코이드였다).^[2]그 두 표면은 서로 접합되어 있다.

스크커 표면은 최소 표면 문제를 제한하는 특정 연구와 쌍곡선 공간의 조화 차이점 연구에서 발생한다.

셰르크의 첫 표면

Scherk의 첫 번째 표면은 서로 직교하는 평행 평면의 두 무한 계열에 대해 점근증이 없으며, 이 둘은 아치의 브리징 패턴에서 z = 0에 가깝게 만난다.그것은 무한히 많은 직선의 수직선을 포함하고 있다.

단순 스크허크 표면의 시공

유클리드 평면의 사각형에서 다음과 같은 최소 표면 문제를 고려한다: 자연수 n의 경우, 일부 함수의 그래프로 최소 표면 σ을_n 찾는다.

${\displaystyle u_{n}:\좌(-{\frac {\pi }{2}},+{\pi }{2}}\오른쪽)\time \좌(-{{\frac {},+{\pi }}}}, \mathb {R}}}}}}}}}}}}$

그런

${\displaystyle \lim _{y\to \pm \pi /2}u_{n}\왼쪽(x,y\오른쪽)=+n{n\text{{{}}}}{{}}}}$

${\displaystyle \lim _{x\to \pm \pi /2}u_{n}\왼쪽(x,y\오른쪽)=-n\text{{{}}}{}-{{}}{{{}}}}}}.}$

즉, 최소_n 표면 방정식을 만족한다.

${\displaystyle \mathrm {div} \left\frac {\bla u_{n}(x,y)}{\sqrt {1+ \bla u_{n}(x,y) ^{2}}\오른쪽)\equiv 0}$

그리고

${\displaystyle \Sigma _{n}=\{(x,y,u_{n})(x,y)\mathb {R}^{3}\왼쪽 -{\frac {\pi }{2}}<x,y>+{\frac{}{}}}}}2}}.\right\}}$

n이 무한대로 작용하는 경향이 있는 제한 표면은 무엇인가?답은 1834년 H. Scherk에 의해 제시되었다: 제한 표면 σ은 다음 그래프 이다.

${\displaystyle u:\{\frac {\pi }{2}},+{\pi }{2}}\오른쪽)\time \left(-{\frac {},+{\pi }}}\mathb {R},},}},}$

${\displaystyle u(x,y)=\log \leftd\frac {\cos(x)}{\cos(y)}}\오른쪽).}$

즉, 광장의 스허크 표면은

$\표시 스타일 \Sigma =\좌측\{\좌측.\left(x,y,\log \left)({\frac {\cos(x)}{\cos(y)}}\right)\in \mathb {R}^{3}\right -{\frac {\pi }{2}}:<x,y<+{\frac{2}}\rig\rig\rig\right}.}$

더 일반적인 Scherk 표면

유클리드 평면의 다른 사분면 측정에서 유사한 최소 표면 문제를 고려할 수 있다.쌍곡선 평면의 사변측정감시에서도 동일한 문제를 고려할 수 있다.2006년에 해롤드 로젠버그와 파스칼 콜린은 쌍곡선 셰르크 표면을 사용하여 복합면에서 쌍곡선 평면(쌍곡선 지표가 있는 단위 디스크)에 이르기까지 조화로운 차이점을 구성하여 쇤-을 반증하였다.어림짐작.

스허크의 두 번째 표면

Scherk의 두 번째 표면은 교차점이 교차하는 터널의 배열로 이루어진 두 개의 직교 평면처럼 전체적으로 보인다.그것의 수평면과 교차하는 부분은 교번 하이퍼볼라로 구성되어 있다.

여기에는 다음과 같은 암묵적 방정식이 있다.

$\displaystyle \sin(z)-\sinh(x)\sinh(y)=0}$

Weierstras-Enneper 매개 변수화 $f{\displaystyle }$( ${\displaystyle z}$)${\displaystyle }$= ${\displaystyle \frac{4\mathrm{}}{}}$ 1${\displaystyle \frac{}{}}$- ${\displaystyle \frac{{z\mathrm{}}^{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\$ $g{\displaystyle }$( ${\displaystyle z}$)${\displaystyle }$= ${\displaystyle i}$ ${\displaystyle z}$ ${\displaystyle$ g$(z)=iz}$을(를)로 파라메트리할 수 있다.^[3]

${\displaystyle x(r,\theta )=2\Re(\ln(1+re^{i\theta })-\ln(1-re^{i\tea })=\ln \왼쪽 \frac {1+r^{2}+2r\cos \theta }{1+r^{2}-2r\cos \theta }}$

${\displaystyle y(r,\theta )=\re (4i\tan^{-1}(re^{i\theta }))=\ln \왼쪽 \frac {1+r^{2}-2r\sin \theta }{1+r^{2}+2r\sin }}$

${\displaystyle z(r,\theta )=\Re (2i(-\ln(1-r^{2}e^{2i\theta })+\ln(1+r^{2}e^{2i\theta }))=2\tan ^{-1}\left({\frac {2r^{2}\sin 2\theta }{r^{4}-1}}\right)}$

$\theta {\displaystyle }$[ ${\displaystyle 0,}$ ${\displaystyle 2}$ ${\displaystyle \pi }$) ${\displaystyle \theta \in [0,2\pi$ $)}$ 및 $r$ ${\displaystyle \in }$($0,1).$ 이것은 표면의 한 기간을 제공하며, 이후 대칭에 의해 z 방향으로 확장될 수 있다$.$

표면은 H. Karcher에 의해 주기적인 최소 표면의 안장탑 계열로 일반화되었다.

다소 혼란스러울 정도로, 이 표면은 때때로 문헌에서 셰르크의 다섯 번째 표면이라고 불린다.^[4][5]혼동을 최소화하기 위해, 그것을 Scherk의 단독 주기적 표면 또는 Scherk-tower라고 부르는 것이 유용하다.

외부 링크

• Sabitov, I.Kh. (2001) [1994], "Scherk surface", Encyclopedia of Mathematics, EMS Press
• MSRI 지오메트리에서의 Scherk의 첫 번째 표면 [2]
• MSRI 지오메트리에서의 Scherk의 두 번째 표면 [3]
• Scherk의 최소 표면은 Mathworld [4]

참조