섹스트 방정식

대수학에서 sextic(또는 hexic) 다항식은 도 6의 다항식이다.6번째 방정식은 6번째 다항식이다. 즉, 왼손이 6번째 다항식이고 오른손은 0인 방정식이다.보다 정확하게는 다음과 같은 형태를 띠고 있다.

${\displaystyle ax^{6}+bx^{5}+cx^{4}+dx^{3}+ex^{2}+dx+g=0,\,}$

여기서 ≠ 0과 계수 a, b, b, c, d, e, f, g는 정수, 합리적인 수, 실수, 복잡한 수 또는 보다 일반적으로 모든 분야의 구성원이 될 수 있다.

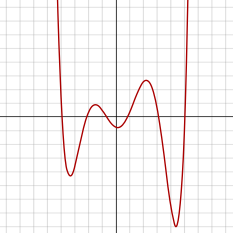
sextic 함수는 sextic 다항식(sextic polyomial)에 의해 정의되는 함수다.짝수도가 있기 때문에 국소 최대값과 국소 최소값이 각각 추가될 수 있다는 점을 제외하고는 그래프를 그릴 때 섹스트 함수가 사분위 함수와 유사하게 나타난다.육분함수의 파생어는 5분함수다.

6차 함수는 짝수 정도의 다항식 함수로 정의되기 때문에, 인수가 양수 또는 음수 무한대로 갈 때 같은 무한 한계를 갖는다.선행 계수 a가 양의 값이면 함수는 양쪽에서 양의 무한대로 증가하며 따라서 함수는 전지구적 최소값을 갖는다.마찬가지로 a가 음수일 경우 sextic 함수는 음의 무한대로 감소하고 글로벌 최대치를 가진다.

해결 가능한 sextics

도끼⁶ + dx³ + g = 0과 같은 일부 6도 방정식은 활성산소로 인자화하여 해결할 수 있지만 다른 6도 방정식은 해결할 수 없다.Evariste Galois는 갈루아 이론의 분야를 발생시킨 급진주의자에 의해 주어진 방정식이 해결될 수 있는지를 결정하기 위한 기술을 개발했다.^[1]

갈루아 이론은 그것의 갈루아 그룹이 두 뿌리의 세 하위 집합으로 이루어진 세 개의 하위 집합으로 이루어진 세트의 분할을 안정화하는 순서 48 그룹이나 또는 뿌리 집합의 분할을 두 하위 집합으로 안정화하는 순서 72 그룹에 포함되는 경우에만 급진적인 측면에서 풀릴 수 있다는 것이다.뿌리를 뽑다

두 경우 모두 시험하는 공식들이 있고, 만약 방정식이 해결 가능하다면, 급진적인 관점에서 뿌리를 계산하라.^[2]

일반 육차 방정식은 캄페 드 페리에트 함수의 관점에서 풀 수 있다.^[1]보다 제한된 등급의 육분법을 펠릭스 클라인의 5분위 방정식 해결 접근법을 이용하여 하나의 변수에서 일반화된 초지하학 함수의 관점에서 해결할 수 있다.^[1]

예

증기기관 조기 작업이라는 맥락에서 발생한 와트의 곡선은 두 변수에서 sixtic이다.

입방정식을 푸는 방법 중 하나는 변수의 입방정식에서 2차 방정식으로 풀 수 있는 6, 3, 0도 항만을 갖는 6차 방정식을 얻기 위한 변수의 변환을 포함한다.

어원

설명자 "섹스트릭"은 라틴어 줄기에서 6번째 또는 6번째("섹스-t-")로, 그리스 접미사는 "인정"을 의미한다.훨씬 덜 흔한 "난독성"은 줄기(헥스-6)와 접미사(-익-) 모두에 그리스어를 사용한다.두 경우 모두 접두사는 함수의 정도를 가리킨다.종종 이러한 유형의 기능은 단순히 "6도 함수"라고 언급될 것이다.

참고 항목

• 케일리의 육식어
• 입방 함수
• 패혈 방정식

참조