수학에서 함수의 대칭 감소 재배열은 대칭적이고 감소하는 함수로서, 수준 집합이 원래 함수의 그것과 같은 크기인 함수다.[1]
집합 정의
할 수 있는 세트가 주어지면, R에서n A  의 대칭 재배열을 정의하는데
의 대칭 재배열을 정의하는데 A라고 하는 공은, 볼륨(Lebeg 측정)이 세트 의 볼륨과 동일하다
A라고 하는 공은, 볼륨(Lebeg 측정)이 세트 의 볼륨과 동일하다

동등한 정의는

여기서 는 단위 공의 볼륨이고, 여기서 A은
단위 공의 볼륨이고, 여기서 A은 (는) 의 볼륨이다
(는) 의 볼륨이다
함수에 대한 정의
수준이 - 1) f )(Y∈ 0 y { 0
)(Y∈ 0 y { 0 로 설정된 음수가
로 설정된 음수가 아닌 측정 가능한 실제 값 f 의 재배치는 유한하다.
아닌 측정 가능한 실제 값 f 의 재배치는 유한하다.

서 는 집합 A의 지표 함수를 나타낸다.즉 ( ) f의 값은
A의 지표 함수를 나타낸다.즉 ( ) f의 값은 : () > }{\\{의 대칭 재배열 이
: () > }{\\{의 대칭 재배열 이 x :{\과 같은 높이 t을
x :{\과 같은 높이 t을 부여한다
부여한다 이러한 정의에 대한 다음과 같은 동기가 있다.왜냐하면 정체성이
이러한 정의에 대한 다음과 같은 동기가 있다.왜냐하면 정체성이

음이 아닌 함수  에 대해 holds non-negative 함수 g A}=\_{A^}}}}}}}}}}을(를) 고정하도록
에 대해 holds non-negative 함수 g A}=\_{A^}}}}}}}}}}을(를) 고정하도록 강제하는 고유한 정의가 된다.
강제하는 고유한 정의가 된다.
특성.
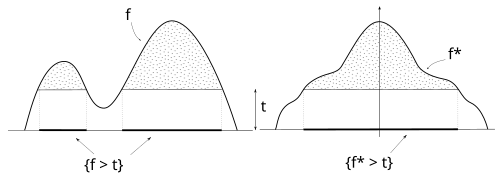
함수와 그 대칭 감소 재배열은 수준 집합의 측도를 보존한다. f는 수준 집합이  의 수준 집합과 동일한 측정값을 갖는 대칭 및 감소 함수다
의 수준 집합과 동일한 측정값을 갖는 대칭 및 감소 함수다 .
.

이 (가) p L의 함수인 경우
(가) p L의 함수인 경우

하디-리틀우드 불평등은 지속된다.

게다가, Polya-Szegh 불평등은 지속된다.은 만약 p f W 이면 라고 되어
만약 p f W 이면 라고 되어 있다.
있다.

대칭 감소 재배열은 L 거리를 보존하고 감소시키는 순서다.
보존하고 감소시키는 순서다.

그리고

적용들
Polya-Szegh 불평등은 한계 사례에서 = 1 }을 를 사용하여 등측 불평등을 산출한다.또한, 조화 함수와의 관계를 이용하여 레일리-파버-크론 불평등을 증명할 수 있다.
를 사용하여 등측 불평등을 산출한다.또한, 조화 함수와의 관계를 이용하여 레일리-파버-크론 불평등을 증명할 수 있다.
비대칭 감소 재배열
또한 f*를 모든 R이n 아닌 음수가 아닌 실수에 대한 함수로 정의할 수 있다.[2]Let (E,μ) be a σ-finite measure space, and let ![{\displaystyle f\colon E\to [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb2554d2aec3476a3fe0ef7e1bf62cfbb1de712f) be a measurable function that takes only finite (i.e., real) values μ-a.e. (where "μ-a.e." means except possibly on a set of μ-measure zero).규칙으로
be a measurable function that takes only finite (i.e., real) values μ-a.e. (where "μ-a.e." means except possibly on a set of μ-measure zero).규칙으로![{\displaystyle \mu _{f}\colon [0,\infty ]\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24491f88892795f6774093c11187b8f2f8e1b2ca) 분배 함수 :[ →[ 0 를 정의한다.
분배 함수 :[ →[ 0 를 정의한다.

이제 규칙으로![{\displaystyle f^{*}\colon [0,\infty )\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a901052c19dbe28a259fc1aa478ffba2b77f920) f의 감소하는 재배열( 때로는 증가하지 않는 재배열)을 :[ 0 )→[ 함수 f,∞ ] [\ f로 정의할 수 있다.
f의 감소하는 재배열( 때로는 증가하지 않는 재배열)을 :[ 0 )→[ 함수 f,∞ ] [\ f로 정의할 수 있다.
![{\displaystyle f^{*}(t)=\inf\{s\in [0,\infty ]\colon \mu _{f}(s)\leq t\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e941b985f70b5060e47eb27a590234d4d4d895f1)
이 감소 재배열 버전은 음수가 아닌 실제 숫자에 대해서만 정의되므로 대칭적이지 않다는 점에 유의하십시오.그러나 위에 열거한 많은 동일한 속성, 즉 다음과 같은 대칭 버전을 계승한다.
- f와 f*는 동일시할 수 있다. 즉, 동일한 분포 함수를 가지고 있다.
- 하디-리틀우드 불평등은 유지된다 즉,i E 0 () ( t) {\ fg\mu \);d\d\\\d

- μ-a
 .e는 g ≤ ≤ { { {\ f g을 의미한다
.e는 g ≤ ≤ { { {\ f g을 의미한다
- f 모든 실수 a에
 .
.
 for all
for all  .
.
- f μ-a
 .e는 ↑ f을(를) 의미한다
.e는 ↑ f을(를) 의미한다
- ) =( ) p}}}{*=( 모든 양의 실수 p에 대해
 .
.
- ( E)= f p[ 0 ,) \ 모든 양의 실수 p에 대해
 .
.

(nonsymmetric) 감소하는 재배열 함수는 흔히 재배열-내변함수 공간 이론에서 발생한다.특히 중요한 것은 다음과 같다.
- 룩셈부르크 표현 정리. 측정 공간, ) 에 대해 rearrange {\ \rho을(를) 재배열-변속 Banach 함수 규범이 되도록
 한다
한다 Then there exists a (possibly not unique) rearrangement-invariant function norm
Then there exists a (possibly not unique) rearrangement-invariant function norm  on
on  such that
such that  for all nonnegative measurable functions 유한 값 μ-a.e인
for all nonnegative measurable functions 유한 값 μ-a.e인![{\displaystyle f\colon E\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82664bb7b7d670532b6a54d45ca1f16e99af5b34) ].
].
상기 정리에서 모든 용어(즉, 바나흐 함수 규범, 재배열-상변형 바나흐 함수 공간, 공명 측정 공간)의 정의는 베넷과 샤플리의 책(cf. 이하 참조) 제1절과 제2절에서 찾을 수 있다.
참고 항목
참조




 (는)
(는) 





 x :
x : 부여한다
부여한다









 만약
만약 




![{\displaystyle f\colon E\to [-\infty ,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb2554d2aec3476a3fe0ef7e1bf62cfbb1de712f)
![{\displaystyle \mu _{f}\colon [0,\infty ]\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24491f88892795f6774093c11187b8f2f8e1b2ca)

![{\displaystyle f^{*}\colon [0,\infty )\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a901052c19dbe28a259fc1aa478ffba2b77f920)
![{\displaystyle f^{*}(t)=\inf\{s\in [0,\infty ]\colon \mu _{f}(s)\leq t\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e941b985f70b5060e47eb27a590234d4d4d895f1)
















![{\displaystyle f\colon E\to [0,\infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82664bb7b7d670532b6a54d45ca1f16e99af5b34)


