삼각 적분

Si(x) (파란색)와 Ci(x) (녹색)은 동일한 플롯에 표시되었다.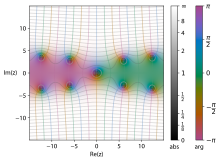

도메인 색상의 변형으로 표시된 복합 평면의 일체형 사인.

복잡한 평면에 코사인 내장. 음의 실제 축을 따라 가지를 자르십시오.

수학에서 삼각 통합은 삼각 함수를 포함하는 통합의 한 계열이다.

사인 적분

0

≤

x

≤

8

π

에 대한 Si(x) 그림.

다양한 사인 적분 정의는

\operatorname {Si}=\int _{0}^{x}{\frac {\sin t}{t}\,dt

\si}=-\int _{x}^{\\inflt}{\frac {\sin t}{t}\,dt~~

통합과 통합에 유의하십시오. $sin$ $x$ x x x $x$ 는 sinc 함수, zerot 구형 Besel 함수. $sinc$ 는 짝수 함수(전체 복잡한 평면에 걸친 홀형체)이기 때문에 $Si$ 는 전체, 홀수, 그리고 그 정의의 적분은 엔드포인트를 연결하는 어떤 경로를 따라 취할 수 있다.

정의상 $Si(x)$ 는 $x$ = $0$ 에서 값이 0인 $x / x$ 의 해독제, $si(x)$ 는 $x$ = $\infty$ 에서 값이 0인 해독제다. 그들의 차이는 디리클레 적분에 의해 주어진다.

\operatorname {Si} (x)-\operatorname {si} (x)=\int _{0}^{\infty }{\frac {\sin t}{t}}\,dt={\frac {\pi }{2}}\quad {\text{ or }}\quad \operatorname {Si} (x)={\frac {\pi }{2}}+\operatorname {si} (x)~.

신호 처리에서 사인 적분(Sine integrated)의 진동은 sinc 필터를 사용할 때 오버슈트 및 링잉 아티팩트를 유발하며, 잘린 sinc 필터를 로우패스 필터로 사용할 경우 주파수 영역 링잉을 유발한다.

깁스 현상과 관련이 있다. 사인 적분을 중량계단 함수와 함께 sinc 함수의 콘볼루션으로 간주한다면 이는 깁스 현상의 원인인 푸리에 시리즈를 잘라내는 것에 해당한다.

코사인 적분

0 <

x

≤ 8π에 대한

Ci(x)

그림.

다른 코사인 적분 정의는

\operatorname {Cin}=\int _{0}^{x}{\frac {1-\cos t}{t}\,dt~~

\operatorname {Ci} (x)=-\int _{x}^{\infty }{\frac {\cos t}{t}}\,dt=\gamma +\ln x-\int _{0}^{x}{\frac {1-\cos t}{t}}\,dt\qquad ~{\text{ for }}~\left \operatorname {Arg} (x)\right <\pi ~,

여기서 γ

0.

57721566

은 오일러-마스케로니 상수다. 일부 텍스트는

ci

대신

ci

를 사용한다.

$Ci(x)$ 는 $cos$ x / x ( $x\to \infty$ → $x\to \infty$ ${\displaystyle x\to \inflt$ }) $x\to \infty$ 로 소멸되는 cos $x$ / $x$ 의 해독제다. 두 정의는 다음에 의해 관련된다.

\operatorname {Ci}(x)=\gamma +\ln x-\operatorname {Cin}(x)~.

$Cin$ 은 짝수, 전체 기능이다. 그러한 이유로, 일부 텍스트는 $Cin$ 을 1차 함수로 취급하고, $Cin$ 의 관점에서 $Ci$ 를 도출한다.

쌍곡 사인 적분

쌍곡선 사인 적분은 다음과 같이 정의된다.

\operatorname {Shi}=\int _{0}^{x}{\frac {\sinh(t)}{t}\,dt.

그것은 다음에 의해 일반 사인 적분과 관련이 있다.

\operatorname {Si}(ix)=i\operatorname {Shi}(x).

쌍곡 코사인 적분

쌍곡 코사인 적분은

\operatorname {Chi}=\gamma +\ln x+\int _{0}^{0}{x}{\frac {\cosh t-1}{t}\dt\qquad ~{\text}}}}}}}}}}}}

여기서

\gamma

\gamma

은

\gamma

(는) 오일러-마스케로니 상수다.

그것은 연속적인 확장을 가지고 있다.

\operatorname {Chi} (x)=\gamma +\ln(x)+{\frac {x^{2}}{4}}+{\frac {x^{4}}{96}}+{\frac {x^{6}}{4320}}+{\frac {x^{8}}{322560}}+{\frac {x^{10}}{36288000}}+O(x^{12}).

보조 기능

삼각적 통합은 소위 "보조함수"의 관점에서 이해할 수 있다.

{\displaystyle{\begin{배열}())&, \equiv&\displaystyle \int _{0}^{\infty}{\frac{\sin(t)}{t+x}}\,dt&, =&,\displaystyle \int _{0}^{\infty}{\frac{e^{-xt}}{t^{2}+1}}\,dt&, =&,\quad\operatorname{ 사}())[{\frac{\pi}{2}}-\operatorname{Si}())\right]\cos())~,\qquad{\text{과}}\\g())&, \equiv&\displays.tyle\int _{0}^{\infty}{\frac{\cos(t)}{t+x}}\,dt&=&\displaystyle \int _{0}^{\infty }{\frac {te^{-xt}}{t^{2}+1}}\,dt&=&-\operatorname {Ci} (x)\cos(x)+\left[{\frac {\pi }{2}}-\operatorname {Si} (x)\right]\sin(x)~.\end{array}}}

이러한 기능을 사용하여 삼각 통합은 (cf)로 다시 표현될 수 있다. 아브라모위츠 & 스테건, 232 페이지)

{\begin{array}{rcl}{\frac {\pi }{2}}-\operatorname {Si} (x)=-\operatorname {si} (x)&=&f(x)\cos(x)+g(x)\sin(x)~,\qquad {\text{ and }}\\\operatorname {Ci} (x)&=&f(x)\sin(x)-g(x)\cos(x)~.\\end{array}}

닐슨의 나선형

$si$ , $ci$ 의 파라메트릭 플롯에 의해 형성된 나선은 닐슨의 나선형으로 알려져 있다.

x(t)=a\reason \ciname {ci}(t)

y(t)=a\display \bename {si}(t)

나선은 프레스넬 통합과 오일러 나선과 밀접한 관련이 있다. 닐슨의 나선은 시각 처리, 도로 및 선로 건설, 기타 분야에 응용이 가능하다.^[1]

팽창

다양한 확장은 인수의 범위에 따라 삼각형 적분 평가에 사용될 수 있다.

점근열(대형 인수의 경우)

\operatorname {Si}(x)\sim {\frac {\pi }{2}}-{\frac {\cos x}}}{x}}\좌측(1-{\frac {2!}}{x^{2}}+{\frac{4!}}{x^{4}}-{\frac {6!}}{x^{6}}}\cdots \오른쪽)-{\frac {\sin x}{x}\{x}\frac {1}{x}-{\frac {3!}}{x^{3}}+{\frac {5!}}{x^{5}}-{\frac {7!}}{x^{7}}}\cdots \오른쪽)

\operatorname {Ci}(x)\심 {\frac {\sin x}{x}}\좌측(1-{\frac {2!}}{x^{2}}+{\frac{4!}}{x^{4}}-{\frac {6!}}{x^{6}}}\cdots \right)-{\frac {\cos x}}{x}\frac {1}{x}-{\frac {3!}}{x^{3}}+{\frac {5!}}{x^{5}}-{\frac {7!}}{x^{7}}}\cdots \right).

series $(x)$ ≫ $1$ 에서 추정과 심지어 정밀한 평가에 사용될 수 있지만, 이 시리즈는 점근성이 없고 다양하다.

컨버전트 시리즈

\operatorname {Si}=\sum _{n=0}^{\frac {(-1)^{n}x^{2n+1}:{n+1}{{{n+1){{{{n+1(2n+1)}!}}}=x-{\frac {x^{3}}{3!\cdot 3}+{\frac{x^{5}{5!\cdot 5}-{\frac {x^{7}}{7!\cdot 7}\pm \cdots }

\operatorname {Ci}(x)=\gamma +\ln x+\sum _{n=1}^{n1}{n1}^{\frac {(-1)^{n}x^{2n}{2n(2n)!}}}=\ln +\ln x-{\frac {{x^{2}}!{2!\cdot2}}+{\frac{x^{4}}{4}}{4!\cdot 4}\mp \cdots

이 시리즈는 어떤 복잡한 $x$ 에서도 수렴되지만, $x$ ≫ $1$ 의 경우 초기에 천천히 수렴하여 높은 정밀도를 위해 많은 항을 필요로 한다.

직렬 팽창의 유도

Maclaurin 시리즈 확장:

\sin \,x=x-{\frac {x^{3}}{3}}{3!2}}+{\frac{x^{5}{5}}{5!}}-{\frac{x^{7}{7}}{7!}}}{\frac{x^{9}}{9!}}-{\frac {{x^{11}}{11!}}}+\cdots

{\frac {\sin \,x}{x}}{x}}=1-{\frac{x^{2}}:{3!}}}{\frac{x^{4}}{5!}}-{\frac{x^{6}}{7!}}}{\frac{x^{8}}{9!}}-{\frac {{x^{10}}{11!}}}+\cdots

\int{\frac {\sin \,x}{x}}dx=x-{\frac {x^{3}}{3}}{3!\cdot 3}+{\frac{x^{5}{5}{5!\cdot 5}-{\frac {x^{7}}{7}}}{\frac {x^{9}}{9!\cdot 9}-{\frac {x^{11}}{11!\cdot 11}+\cdots

가상 인수의 지수적 적분과의 관계

함수

\operatorname {E} _{1}(z)=\int_{1}^{1}{\frac {\exp(-zt)}{t}\,dt\qquad ~{\text{}{}}}}}}{}~\Re(z)\geq 0

지수 적분이라고 불린다.

Si

와

Ci

와 밀접한 관련이 있으며,

\operatorname {E} _{1}(ix)=i\left(-{\frac {\pi }{2}}+\operatorname {Si} (x)\right)-\operatorname {Ci} (x)=i\operatorname {si} (x)-\operatorname {ci} (x)\qquad ~{\text{ for }}~x>0~.

각 함수는 인수의 음수 값에서의 절단을 제외하고 분석적이기 때문에 관계의 타당성 영역을 (이 범위를 벗어나면 $integer$ 의 정수인 추가 항이 표현에 나타난다)로 확장해야 한다.

일반화된 정수 함수의 상상적 인수의 예는 다음과 같다.

\int _{1}^{\infty }\cos(ax){\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}+\sum _{n\geq 1}{\frac {(-a^{2})^{n}}{(2n)!(2n)^{2}}}~,

의 진짜 부분

\int _{1}^{\infty }e^{iax}{\frac {\ln x}{x}}\,dx=-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a\right)+{\frac {\ln ^{2}a}{2}}-{\frac {\pi }{2}}i\left(\gamma +\ln a\right)+\sum _{n\geq 1}{\frac {(ia)^{n}}{n!n^{2}}}~.

유사하게

\int _{1}^{\infty }e^{iax}{\frac {\ln x}{x^{2}}}\,dx=1+ia\left[-{\frac {\pi ^{2}}{24}}+\gamma \left({\frac {\gamma }{2}}+\ln a-1\right)+{\frac {\ln ^{2}a}{2}}-\ln a+1\right]+{\frac {\pi a}{2}}{\Bigl (}\gamma +\ln a-1{\Bigr )}+\sum _{n\geq 1}{\frac {(ia)^{n+1}}{(n+1)!n^{2}}}~.

효율평가

수렴성 테일러 시리즈의 파데 근사치는 작은 논쟁에 대한 기능을 평가하는 효율적인 방법을 제공한다. Roewe 외 연구진(2015)^[2]이 제공한 다음 $공식$ 은 0 $x$ x $4$ 4의 $경우 -16$ 10보다 더 정확하다.

{\displaystyle{\begin{배열}{rcl}\operatorname{Si}())&, \approx&x\cdot \left(10^{-2}\cdot x^{2}+1.15457225751016682\cdot 10^{-3}\cdot x^{4}-1.41018536821330254\cdot 10^{-5}\cdot x^{6}\\~~~+9.43280809438713025\cdot 10^{-8}\cdot x^{8}-3.53201978997168357\cdot 10^{에서}\cdot x^{10}+7.08240282{\frac{\begin{배열}{나는}1-4.54393409816329991\cdot.274875911\cdot 10^{-13}\cdot x^{12}\\~~~-6.05338212010422477\cdot 10^{-16}\cdot x^{14}\end{array}}{\begin{array}{l}1+1.01162145739225565\cdot 10^{-2}\cdot x^{2}+4.99175116169755106\cdot 10^{-5}\cdot x^{4}+1.55654986308745614\cdot 10^{-7}\cdot x^{6}\\~~~+3.28067571055789734\cdot 10^{-10}\cdot x^{8}+4.5049097575386581\cdot 10^{-13}\cdot x^{10}+3.21107051193712168\cdot 10^{-16}\cdot x^{12}\end{array}}\오른쪽)\\&, ~&,\\\operatorname{ 사}())&, \approx&\gamma +\ln())+\\&, &, x^{2}\cdot \left(10^{-3}\cdot x^{2}-1.27528342240267686\cdot 10^{-4가}\cdot x^{4}+1.05297363846239184\cdot 10^{-6}\cdot x^{6}\\~~~-4.68889508144848019\cdot 10^{-9}\cdot x^{8}+1.06480802891189243\cdot 10^{-11}\cdot x^{\frac{\begin{배열}{나는}-0.25+7.51851524438898291\cdot.{10}-9.93728488857585407\cdot 10^{-15}\cdot x^{12}\\\end{array}}{\begin{array}{l}1+1.1592605689110735\cdot 10^{-2}\cdot x^{2}+6.72126800814254432\cdot 10^{-5}\cdot x^{4}+2.55533277086129636\cdot 10^{-7}\cdot x^{6}\\~~~+6.97071295760958946\cdot 10^{-10}\cdot x^{8}+1.38536352772778619\cdot 10^{-12}\cdot x^{10}+1.89106054713059759\cdot 10^{-15}\cdot x^{12}\\~~~+1.39759616731376855\cdot 10^{-18}\cdot x^{14}\\end{array}\오른쪽)\end{array}}}}

통합은 다음에 의해 정의된 보조 $f(x)$ f $f(x)$ ( x $f(x)$ ) ${\displaystyle f($ $g(x)$ $)}$ 및 $g(x)$ ( x $g(x)$ ) $g(x)$ 을 통해 간접적으로 평가할 수 있다 $g(x)$

$\operatorname {Si}(x)={\frac {\pi }{2}}-f(x)\cos(x)-g(x)\sin(x)$		$\operatorname {Ci}(x)=f(x)\sin(x)-g(x)\cos(x)$
또는 동등하게
$f(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si}(x)\right]\cos(x)+\operatorname {Ci}(x)\sin(x)$		$g(x)\equiv \left[{\frac {\pi }{2}}-\operatorname {Si}(x)\right]\sin(x)-\operatorname {Ci}(x)\cos(x)$

$x\geq 4$ $x\geq 4$ $x\geq 4$ ${\displaystyle$ x $\geq 4}$ 의 $x\geq 4$ 경우 오류 수가 10보다⁻¹⁶ 작은 $f(x)$ 에서 $g(x)$ 대략 $f(x)$ ( x $f(x)$ ) $f(x)$ 및 $f(x)$ $g(x)$ ( $g(x)$ ) $g(x)$ 아래에 제공된 Padé 합리적 함수:^[2]

{\displaystyle{\begin{배열}())&, \approx&{\dfrac{1}{)}}\cdot \left({\frac{\begin{배열}{나는}1+7.44437068161936700618\cdot 10^{2}\cdot x^{-2}+1.96396372895146869801\cdot 10^{5}\cdot x^{-4가}+2.37750310125431834034\cdot 10^{7}\cdot x^{-6}\\~~~+1.43073403821274636888\cdot 10^{9}\cdot x^{-8}+4.33736238870432522765\cdot 10^{10}\cdot x^{에서}.+6.40533830574022022911\cdot 10^{11}\cdot x^{-12}\\~~~+4.20968180571076940208\cdot 10^{12}\cdot x^{-14}+1.00795182980368574617\cdot 10^{13}\cdot x^{-16}+4.94816688199951963482\cdot 10^{12}\cdot x^{-18}\\~~~-4.94701168645415959931\cdot 10^{11}\cdot x^{-20}\end{array}}{\begin{array}{l}1+7.46437068161927678031\cdot 10^{2}\cdot x^{-2}+1.97865247031583951450\cdot 10^{5}\cdot x^{-4}+2.41535670165126845144\cdot 10^{7}\cdot x^{-6}\\~~~+1.47478952192985464958\cdot 10^{9}\cdot x^{-8}+4.58595115847765779830\cdot 10^{10}\cdot x^{-10}+7.08501308149515401563\cdot 10^{11}\cdot x^{-12}\\~~~+5.06084464593475076774\cdot 10^{12}\cdot x^{-14}+1.43468549171581016479\cdot 10^{13}\cdot x^{-16}+1.11535493509914254097\cdot 10^{13}\cdot x^{-18}\end{array}}\오른쪽)\\&, &, \\g())&, \approx&{\dfrac{1}{x^{2}}}\cdot \left({\frac{\begin{배열}{나는}1+8.1359520115168615\cdot 10^{2}\cdot x^{-2}+2.35239181626478200\cdot 10^{5}\cdot x^{-4가}+3.12557570795778731\cdot 10^{7}\cdot x^{-6}\\~~~+2.06297595146763354\cdot 10^{9}\cdot x^{-8}+6.83052205423625007\cdot 10^{10}\cdot x^{에서}+1.09049528450362786\cdot 10^{12}.\cdot x^{-12}\\~~~+7.57664583257834349\cdot 10^{12}\cdot x^{-14}+1.81004487464664575\cdot 10^{13}\cdot x^{-16}+6.43291613143049485\cdot 10^{12}\cdot x^{-18}\\~~~-1.36517137670871689\cdot 10^{12}\cdot x^{-20}\end{array}}{\begin{array}{l}1+8.19595201151451564\cdot 10^{2}\cdot x^{-2}+2.40036752835578777\cdot 10^{5}\cdot x^{-4}+3.26026661647090822\cdot 10^{7}\cdot x^{-6}\\~~~+2.23355543278099360\cdot 10^{9}\cdot x^{-8}+7.87465017341829930\cdot 10^{10}\cdot x^{-10}+1.39866710696414565\cdot 10^{12}\cdot x^{-12}\\~~~+1.17164723371736605\cdot 10^{13}\cdot x^{-14}+4.01839087307656620\cdot 10^{13}\cdot x^{-16}+3.99653257887490811\cdot 10^{13}\cdot x^{-18}\end{array}}}\right)\\\end{array}}}

참고 항목

참조

^ Gray (1993). Modern Differential Geometry of Curves and Surfaces. Boca Raton. p. 119.
^ ^a ^b Rowe, B.; et al. (2015). "GALSIM: The modular galaxy image simulation toolkit". Astronomy and Computing. 10: 121. arXiv:1407.7676. Bibcode:2015A&C....10..121R. doi:10.1016/j.ascom.2015.02.002. S2CID 62709903.

Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 5". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 231. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.

추가 읽기

Mathar, R.J. (2009). "Numerical evaluation of the oscillatory integral over exp(i $π$ x)·x^1/x between 1 and ∞". Appendix B. arXiv:0912.3844 [math.CA].
Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. (2007). "Section 6.8.2 – Cosine and Sine Integrals". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8.
Sloughter, Dan. "Sine Integral Taylor series proof" (PDF). Difference Equations to Differential Equations.
Temme, N.M. (2010), "Exponential, Logarithmic, Sine, and Cosine Integrals", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248

외부 링크

http://mathworld.wolfram.com/SineIntegral.html
"Integral sine", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
"Integral cosine", Encyclopedia of Mathematics, EMS Press, 2001 [1994]

[1] Gray (1993). Modern Differential Geometry of Curves and Surfaces. Boca Raton. p. 119.

[RoweEtAl2015-2] Rowe, B.; et al. (2015). "GALSIM: The modular galaxy image simulation toolkit". Astronomy and Computing. 10: 121. arXiv:1407.7676. Bibcode:2015A&C....10..121R. doi:10.1016/j.ascom.2015.02.002. S2CID 62709903.

[1]

[2]

Search