잘린 십이면체

잘린 십이면체

유형	균일성 다면체
요소들	F = 54, E = 180 V = 120 (표준 = -6)
측면 나란히	30{4}+12{10}+12{10/3}
위토프 기호	2 5 5/3
대칭군	I_h, [5,3], *532
색인 참조	U₅₉, C₇₅, W₉₈
이중 다면체	중앙 디디아키스 3면체
꼭지점 도형	4.10/9.10/3
Bowers 약자	quitd

잘린 12면체의 3D 모형

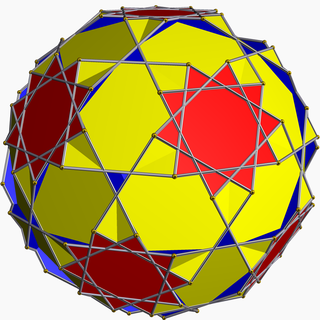
기하학에서, 잘린 도데카데면체(또는 스텔라트런 절단 도데카데면체)는 U로₅₉ 색인화된 비볼록 균일한 다면체이다. 그것은 Schléfli 기호_0,1,2 t{5⁄3,5. 54개의 면(30개의 정사각형, 12개의 데카곤, 12개의 데카그램), 180개의 모서리, 120개의 ^[1]정점이 있습니다.다면체의 중앙 영역은 20개의 작은 삼각형 구멍을 통해 외부와 연결됩니다.

잘린 12면체라는 이름은 다소 오해의 소지가 있다: 12면체를 잘라내면 정사각형보다는 직사각형 면이 생성될 것이고, 12면체의 5면체는 10면체보다는 잘린 5각형 면으로 변할 것이다.그러나 콕서터, 롱게트-하이긴스 & 밀러(1954)[2]에 의해 정의된 12면체의 준이성화이다.이러한 이유로, 그것은 준달 모양으로 깎인 ^[3]십이지장면체로도 알려져 있다.콕서터 등은 1881년 오스트리아 수학자 요한 ^[4]피치가 발표한 논문으로 이 발견의 공로를 돌렸다.

데카르트 좌표

잘린 12면체의 정점에 대한 데카르트 좌표는 다음과 같은 점으로부터 원형 이동 및 부호 변화를 통해 얻은 모든 수의 3배이다(여기서 $\tau ={\frac {1+{\sqrt {5}}}{2}}$ $\tau ={\frac {1+{\sqrt {5}}}{2}}$ $\tau ={\frac {1+{\sqrt {5}}}{2}}$ + $\tau ={\frac {1+{\sqrt {5}}}{2}}$ 2 \ $displaystyle = style frac$ { 1 + { \ $displayrt$ { $5}}}$ {2 $\tau ={\frac {1+{\sqrt {5}}}{2}}$ } $\tau ={\frac {1+{\sqrt {5}}}{2}}$ ））。

\displaystyle (1,1,3);\displays({\frac {1}{\displays }), {\frac ^{2}}, 2\displays };\displays(\frac {2}), \displays(\displays ^{2}},\displays ^{2};\displays});\frac {1}, {\displays},\frac {1},\dic},\frac {\d},\frac},\d},\displays},}

이들 5개의 점에는 각각 8개의 가능한 표지 패턴과 3개의 가능한 원형 이동이 있어 총 120개의 다른 점이 있습니다.

케일리 그래프로

잘린 12면체는 두 개의 그룹 구성원에 의해 생성된 5개의 요소에 대해 대칭 그룹에 대한 케일리 그래프를 형성합니다. 하나는 5개의 태플의 처음 두 개의 요소를 교환하는 것이고 다른 하나는 마지막 4개의 요소에 대해 원형 이동 연산을 수행하는 것입니다.즉, 다면체의 120개의 정점은 5개의 요소의 5! 순열과 1대 1로 대응하여 배치될 수 있으며, 각 정점의 3개의 이웃이 처음 두 개의 요소를 교환하거나 마지막 4개의 ^[5]요소를 순환적으로 이동함으로써 형성되는 3개의 순열이 되도록 할 수 있다.

「」를 참조해 주세요.

균일한 다면체 목록

레퍼런스

^ Maeder, Roman. "59: truncated dodecadodecahedron". MathConsult.{{cite web}}: CS1 maint :url-status (링크)
^ Coxeter, H.S.M.;Longuet-Higgins, M.S., 밀러, J.C.P.(1954년),"다면체 통일", 왕립 학회 런던의 철학적 거래.시리즈 A수학 및 물리적 과학, 246:401–450, Bibcode:1954RSPTA.246..401C, doi:10.1098/rsta.1954.0003, JSTOR 91532, MR0062446.. 114, 판 IV페이지의 주 411에 quasitruncation 특히 기술과 그림의 골격 모델의 사진을 참조하십시오.
^ Wenninger는 "사분할된 12면체"라고 쓰고 있지만, 이것은 실수로 보인다.
^ 콕서터, Longuet-Higgins & Miller(1954)에 따르면 잘린 십이지장면체는 페이지 86에서 XI로 나타난다Pitsch, Johann (1881), "Über halbreguläre Sternpolyeder", Zeitschrift für das Realschulwesen, 6: 9–24, 72–89, 216.
^ 를 클릭합니다Eppstein, David (2008), "The topology of bendless three-dimensional orthogonal graph drawing", in Tollis, Ioannis G.; Patrignani, Marizio (eds.), Proc. 16th Int. Symp. Graph Drawing, Lecture Notes in Computer Science, vol. 5417, Heraklion, Crete: Springer-Verlag, pp. 78–89, arXiv:0709.4087, doi:10.1007/978-3-642-00219-9_9.

Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208

외부 링크

[1] Maeder, Roman. "59: truncated dodecadodecahedron". MathConsult.{{cite web}}: CS1 maint :url-status (링크)

[2] Coxeter, H.S.M.;Longuet-Higgins, M.S., 밀러, J.C.P.(1954년),"다면체 통일", 왕립 학회 런던의 철학적 거래.시리즈 A수학 및 물리적 과학, 246:401–450, Bibcode:1954RSPTA.246..401C, doi:10.1098/rsta.1954.0003, JSTOR 91532, MR0062446.. 114, 판 IV페이지의 주 411에 quasitruncation 특히 기술과 그림의 골격 모델의 사진을 참조하십시오.

[3] Wenninger는 "사분할된 12면체"라고 쓰고 있지만, 이것은 실수로 보인다.

[4] 콕서터, Longuet-Higgins & Miller(1954)에 따르면 잘린 십이지장면체는 페이지 86에서 XI로 나타난다Pitsch, Johann (1881), "Über halbreguläre Sternpolyeder", Zeitschrift für das Realschulwesen, 6: 9–24, 72–89, 216.

[5] 를 클릭합니다Eppstein, David (2008), "The topology of bendless three-dimensional orthogonal graph drawing", in Tollis, Ioannis G.; Patrignani, Marizio (eds.), Proc. 16th Int. Symp. Graph Drawing, Lecture Notes in Computer Science, vol. 5417, Heraklion, Crete: Springer-Verlag, pp. 78–89, arXiv:0709.4087, doi:10.1007/978-3-642-00219-9_9.

[1]

[3]

[4]

[5]

v t 다면체 항법사
케플러-포인소트 다면체(비볼록형) 일반 다면체)	작은 젤리 모양의 12면체 대십이면체 대스텔레이트 십이면체 대이십면체
균일한 자르기 케플러 포인소트의 다면체	12면체 잘린 12면체 마름모꼴 12면체 잘린 십이십이면체 스너브 도데카데면체 대이십이면체 잘린 대이십면체 비볼록 대마름모십이면체 대절단 정이십이면체
비볼록 균일 반다면체	사십육면체 입방정면체 팔면체 작은 십이십이면체 작은 정이십이면체 대십이지장십이면체 대이십이면체 대십이지육면체 작은 십이지육면체
비볼록 이중 균일 다면체	내측 마름모꼴 삼면체 작은 스텔라펜타키스 12면체 내측 삼각근 육면체 소형 마름모꼴데카크론 내측 오각형 육면체 내측 디디아키스 삼면체 대마름모꼴 삼면체 대스텔라펜타키스 12면체 대탈상 육면체 그레이트 디디아키스 삼면체 대오각 육면체
비볼록 이중 와 균일한 다면체 무한대 스텔레이션	테트라헤미헥사크론 헥사헥타크론 옥타헥타크론 소형 도데카헤미도데카크론 작은 이코시헤미도데카크론 대도데카헤미도데카크론 대이코시헤미도데카크론 대도데카헤미코사크론 소형 도데카헤미코사크론

Search

잘린 십이면체

네임스페이스

더

목차

데카르트 좌표

케일리 그래프로

관련 다면체

중앙 디디아키스 3면체

「」를 참조해 주세요.

레퍼런스

외부 링크

중앙 디디아키스 3면체

유형	별 다면체
얼굴
요소들	F = 120, E = 180 V = 54 (최소값 = -6)
대칭군	I_h, [5,3], *532
색인 참조	DU₅₉
이중 다면체	잘린 십이면체

Search

잘린 십이면체

데카르트 좌표

케일리 그래프로

관련 다면체

중앙 디디아키스 3면체

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.