옥타헤미오크타헤드론

옥타헤미오크타헤드론
유형	균일성 다면체
요소들	F = 12, E = 24 V = 12(수평 = 0)
옆얼굴	8{3}+4{6}
와이토프 기호	3/2 3 3
대칭군	Oh, [4,3], *432
색인 참조	U03, C37, W68
이중 다면체	옥타헤미옥타크론
정점수	3.6.3/2.6
보우어 약자	오호

기하학에서 8각형 또는 알로테트라헤드론은 U로₃ 색인된 비콘벡스 균일한 다면체로서 12면(삼각형 8개와 육각형 4개), 24개의 가장자리, 12개의 꼭지점을 가지고 있다.^[1]그것의 꼭지점 모양은 교차된 사각형이다.

그것은 9개의 혈중합체 중 하나로, 4개의 육각형 면이 모델 중심을 통과한다.

방향성

방향성이 있는 유일한 혈중합체이며, 오일러 특성이 0(위상학적 토러스)인 유일한 균일한 다면체다.

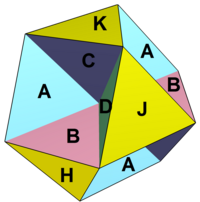옥타헤미오크타헤드론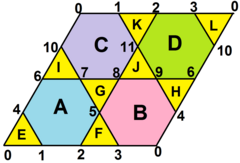

얼굴의 위상 그물은 8개의 삼각형과 4개의 육각형으로 나뉜 회전체로 배열할 수 있다.모든 정점 각도 결함은 0이다.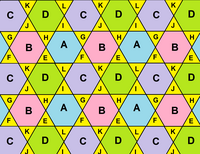

그물은 3헥사형 타일링 평면의 한 영역을 나타낸다.

관련 다면체

정점 배열과 가장자리 배열을 큐보타헤드론(삼각형 면을 공통으로 함), 큐보헤미오크타헤드론(육각형 면을 공통으로 함)과 공유한다.

와이토프 건설에 의해 큐옥타헤드론에 대한 rhombitetratratetrahedron 구조와 같이 4면 대칭(T_d)을 가지며, 역방향으로 대체 삼각형을 가지고 있다.삼각형이 교대하지 않으면 팔면대칭(O_h)을 가진다.

큐폭타헤드론		큐보헤미오크타헤드론	옥타헤미오크타헤드론
팔면 대칭	사면 대칭		팔면 대칭	사면 대칭
2 3 4	3 3 2	4/3 4 3 (이중 커버)		3/2 3 3

---

옥타헤미옥타크론

옥타헤미옥타크론
유형	별다면체
면	—
요소들	F = 12, E = 24 V = 12(수평 = 0)
대칭군	Oh, [4,3], *432
색인 참조	DU03
이중 다면체	옥타헤미오크타헤드론

옥타헤미오크타크론은 옥타헤미오크타헤드론의 이중으로, 9개의 이중혈모체 중 하나이다.그것은 육각류에서 시각적으로 불분명하게 보인다.

혈중수체는 중심을 통과하는 면이 있기 때문에, 이중 수치는 무한에 해당하는 정점을 가지고 있으며, 적절히 무한의 실제 투영 평면에 있다.^[2]Magnus Wenninger의 Dual Models에서는 대칭을 유지하기 위해 각각 양방향으로 무한대의 동일한 꼭지점까지 확장되는 교차 프리즘으로 표현된다.실제로 모델 프리즘은 제조자에게 편리한 특정 지점에서 잘려진다.Wenninger는 이 수치들이 무한대로의 stellation이라 불리는 새로운 종류의 stellation figures의 멤버라고 제안했다.그러나 그는 또한 엄밀히 말하면 다면체의 구조가 일반적인 정의에 부합하지 않기 때문에 다면체는 아니라고 제안했다.

옥타헤미오ctacron은 무한대에 네 개의 정점을 가지고 있다.

참고 항목

• 5옥타헤미오크타헤드라 화합물
• 헤미-큐브 - 무한대의 네 정점은 이 추상적인 다면체의 네 정점에 방향적으로 대응한다.

참조

• Wenninger, Magnus (2003) [1983], Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 (101페이지, 혈중합체(9)의 듀얼스)

외부 링크

• Eric W. Weisstein, Octahemioctahedron (Uniform polyhedron) at MathWorld.
• Weisstein, Eric W. "Octahemioctacron". MathWorld.
• 균일한 다면체 및 듀얼