투란 그래프

투란 그래프
투란 그래프
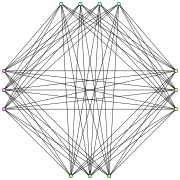	투란 그래프 T(13,4)
이름은 다음과 같습니다.	팔 투란
꼭짓점
가장자리	~(- ) n }\right
반지름
지름
걸스
색수
표기법
	그래프 및 매개변수 표

$T(n,r)$ $T(n,r)$ ${\displaystyle T(n,$ r $)}$ 로 표시되는 $T(n,r)$ Turán 그래프는 완전한 다중 분할 그래프이며, $n$ ${\displaystyle$ n $}개$ 의 정점 $n$ 집합을 r ${\display$ r $}$ 의 $r$ 부분 집합으로 분할하고 크기가 가능한 한 동일한 다음 두 정점을 서로 다른 부분 집합에 속하는 경우에만 간선으로 연결합니다. Where $q$ and $s$ are the quotient and remainder of dividing $n$ by $r$ (so $n=qr+s$ ), the graph is of the form $K_{q+1,q+1,\ldots ,q,q}$ , 변의 수는

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

-

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

)

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

2

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

-

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

+

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

(

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

2

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

)

{\

r}\

right){\frac {n^{2}-s^{2}}+{s \선택

2

\left(1-{\frac {1}{r}}\right){\frac {n^{2}-s^{2}}{2}}+{s \choose 2}

The graph has $s$ subsets of size $q+1$ , and $r-s$ subsets of size $q$ ; each vertex has degree $n-q-1$ or $n-q$ . $r$ $n$ 이 r ${\displaystyle$ r $}($ 즉, $s=0$ = 0 ${\$ displaystyle s = 0}인 경우 정규 그래프입니다.

투란 정리

투란 그래프는 극지 그래프 이론에서 중요한 결과인 투란의 정리를 증명하는 데 사용한 팔 투란의 이름을 따서 명명되었습니다.

비둘기집 원리에 의해, 투란 그래프의 모든 r+1개의 정점 집합은 동일한 분할 부분 집합에 있는 두 개의 정점을 포함하므로, 투란 그래프는 크기 r+1의 클릭을 포함하지 않습니다. Turán의 정리에 따르면, Turán 그래프는 n개의 정점을 갖는 모든 (r + 1)-클릭이 없는 그래프 중에서 가능한 최대 수의 간선을 갖습니다. 키바시와 수다코프(2003)는 투란 그래프가 αn 꼭짓점의 모든 부분 ${\frac {r\,{-}\,1}{3r}}(2\alpha -1)n^{2}$ 이 적어도 r ${\frac {r\,{-}\,1}{3r}}(2\alpha -1)n^{2}$ - ${\frac {r\,{-}\,1}{3r}}(2\alpha -1)n^{2}$ ${\frac {r\,{-}\,1}{3r}}(2\alpha -1)n^{2}$ ( ${\frac {r\,{-}\,1}{3r}}(2\alpha -1)n^{2}$ α ${\frac {r\,{-}\,1}{3r}}(2\alpha -1)n^{2}$ ${\frac {r\,{-}\,1}{3r}}(2\alpha -1)n^{2}$ ${\frac {r\,{-}\,1}{3r}}(2\alpha -1)n^{2}$ 2 {\ $displaystyle {\frac$ {r $\,{-}\,1$ }{ $3r}(2\alpha$ -1) $n^{2}$ 가장자리에 ${\frac {r\,{-}\,1}{3r}}(2\alpha -1)n^{2}$ 걸쳐 있는 유일한 (r + 1)-클릭 없는 순서의 그래프임을 보여줍니다. 만약 α가 1에 충분히 가깝다면. 에르트 ő스-스톤 정리는 고정된 투란 그래프가 없는 그래프의 간선 수를 부분 그래프로 묶어 투란의 정리를 확장합니다. 이 정리를 통해 서브그래프의 색수에 따라 제외된 서브그래프에 대해 극한 그래프 이론의 유사한 경계가 입증될 수 있습니다.

특수한 경우

Turán 그래프에서 모수 r을 몇 가지 선택하면 독립적으로 연구된 주목할 만한 그래프를 얻을 수 있습니다.

Turán 그래프 T(2n,n)는 완전한 그래프_2n K에서 완전한 일치를 제거함으로써 형성될 수 있습니다. Roberts(1969)가 보여주었듯이, 이 그래프는 정확히 n의 상자성을 가지며, 때때로 Roberts 그래프로 알려져 있습니다. 이 그래프는 n차원 교차 폴리토프의 1-skeleton이기도 합니다. 예를 들어, 그래프 T(6,3) = K는 정팔면체의 그래프인 팔면체 그래프입니다. 만약 n쌍의 커플이 파티에 가고, 각 커플이 파트너를 제외한 모든 사람과 악수를 한다면, 이 그래프는 악수의 집합을 설명합니다. 이러한 이유로 칵테일 파티 그래프라고도 불립니다.

Turán 그래프 T(n,2)는 완전한 이분 그래프이며 n이 짝수일 때 무어 그래프입니다. r이 n의 약수일 때, Turán 그래프는 대칭적이고 강한 규칙성을 갖지만, 일부 저자는 Turán 그래프를 강한 규칙성을 갖는 사소한 경우로 간주하여 강한 규칙성 그래프의 정의에서 제외합니다.

Turán 그래프의 클래스는 지수적으로 많은 최대 클리크를 가질 수 있으며, 이는 이 클래스가 적은 클리크를 갖지 않는다는 것을 의미합니다. 예를 들어, Turán 그래프 $T$ ⌈ $T(n,\lceil n/3\rceil )$ n / $3$ ⌉) ${\displaystyle$ T( $n,\$ lceil n / 3\rceil )}에는 32개의 최대 클리크가 있으며, 여기서 3a + 2b = n 및 b ≤ 2이며, 각 최대 클리크는 각 파티션 하위 집합에서 하나의 정점을 선택하여 형성됩니다. 이는 그래프의 간선 수(Moon and Moser 1965)에 관계없이 모든 n개의 정점 그래프 중에서 가능한 최대 클리킹 수가 가장 많습니다. 이러한 그래프를 Moon-Moser 그래프라고 부르기도 합니다.

기타속성

모든 Turán 그래프는 코그래프입니다. 즉, 서로소인 결합과 여집합 연산에 의해 개별 정점에서 형성될 수 있습니다. 구체적으로, 이러한 순서는 Turán 그래프의 각 독립 집합을 고립된 정점의 서로소 결합으로 형성하는 것으로 시작할 수 있습니다. 그러면 전체적인 그래프는 이러한 독립적인 집합들의 여집합들의 서로소 결합의 여집합입니다.

Chao와 Novacky(1982)는 Turán 그래프가 색적으로 유일하다는 것을 보여줍니다. 다른 그래프는 동일한 색다항식을 가지고 있지 않습니다. Nikiforov(2005)는 Turán 그래프를 사용하여 그래프의 k번째 고유값과 그 보수의 합에 대한 하한을 제공합니다.

Falls, Powell 및 Snoeyink는 데이터를 그래프로 표현하고 큰 Turán 하위 그래프를 검색하여 유전체 데이터에서 이종 유전자 그룹의 클러스터를 찾는 효율적인 알고리즘을 개발합니다.

투란 그래프는 기하학적 그래프 이론과 관련된 몇 가지 흥미로운 특성도 가지고 있습니다. Pór and Wood (2005)는 Turán 그래프의 3차원 그리드 임베딩 볼륨에 ω(rn)의 하한을 제공합니다. Witsenhausen(1974)은 R에서^d 단위 지름을 갖는 n개의 점들 중 거리 제곱의 최대 합이 정규 심플의 꼭짓점에 Turán 그래프를 내장하여 형성된 구성에 대해 달성된다고 추측합니다.

n-정점 그래프 G는 G가 r색을 갖는 균등한 색을 인정하는 경우에만 Turán 그래프 T(n,r)의 부분 그래프입니다. Turán 그래프를 독립적인 집합으로 분할하는 것은 G를 색상 클래스로 분할하는 것에 해당합니다. 특히 Turán 그래프는 r-color equitable color을 가진 독특한 극대 n-vertex 그래프입니다.

참고문헌

Chao, C. Y.; Novacky, G. A. (1982). "On maximally saturated graphs". Discrete Mathematics. 41 (2): 139–143. doi:10.1016/0012-365X(82)90200-X.
Falls, Craig; Powell, Bradford; Snoeyink, Jack. "Computing high-stringency COGs using Turán type graphs" (PDF). {{cite journal}}: 저널 인용 요구사항 journal= (도와주세요)
Keevash, Peter; Sudakov, Benny (2003). "Local density in graphs with forbidden subgraphs" (PDF). Combinatorics, Probability and Computing. 12 (2): 139–153. doi:10.1017/S0963548302005539. S2CID 17854032.
Moon, J. W.; Moser, L. (1965). "On cliques in graphs". Israel Journal of Mathematics. 3: 23–28. doi:10.1007/BF02760024. S2CID 9855414.
Nikiforov, Vladimir (2007). "Eigenvalue problems of Nordhaus-Gaddum type". Discrete Mathematics. 307 (6): 774–780. arXiv:math.CO/0506260. doi:10.1016/j.disc.2006.07.035.
Pór, Attila; Wood, David R. (2005). "No-three-in-line-in-3D". Proc. Int. Symp. Graph Drawing (GD 2004). Lecture Notes in Computer Science no. 3383, Springer-Verlag. pp. 395–402. doi:10.1007/b105810. hdl:11693/27422.
Roberts, F. S. (1969). Tutte, W.T. (ed.). "On the boxicity and cubicity of a graph". Recent Progress in Combinatorics: 301–310.
Turán, P. (1941). "Egy gráfelméleti szélsőértékfeladatról (On an extremal problem in graph theory)". Matematikai és Fizikai Lapok. 48: 436–452.
Witsenhausen, H. S. (1974). "On the maximum of the sum of squared distances under a diameter constraint". American Mathematical Monthly. 81 (10): 1100–1101. doi:10.2307/2319046. JSTOR 2319046.

외부 링크

Search