This is a good article. Click here for more information.

3가지 유틸리티 문제

Three utilities problem
"물, 가스, 전기"는 여기서 리다이렉트됩니다.유틸리티에 대해서는, 「Public Utility」를 참조해 주세요.하수도, 가스, 전기 소설에 대해서는 매트 러프를 참고하세요.
평면 내의 선을 나타내는 세 가지 유틸리티 문제의 다이어그램.각 주택은 연결선이 교차하지 않고 각 유틸리티에 연결할 수 있습니까?
Tomsen 그래프 3, 이라고도 하는 유틸리티 그래프의 두 가지 보기

세 가지 유틸리티 문제 또는 때로는 물, 가스 및 전기로 알려진 고전적인 수학 퍼즐은 비행기에서 세 개의 집과 세 개의 유틸리티 회사 사이에 교차하지 않는 연결을 그리도록 요구합니다.20세기 초에 이것을 제안했을 때, 헨리 두데니는 이미 오래된 문제라고 썼다.이것은 불가능한 퍼즐이다: 9개의 선을 모두 교차하지 않고 연결하는 것은 불가능하다.Torus 또는 Möbius 스트립과 같은 평면 외 표면에 있는 문제 또는 다른 주택이나 유틸리티를 통해 연결할 수 있는 버전의 문제를 해결할 수 있습니다.

이 퍼즐은 집을 나타내는 정점과 그 연결을 나타내는 효용과 가장자리가 있는 완전한 초당 3, K_이 평면에 그래프를 포함하는지 물어봄으로써 위상 그래프 이론의 문제로 공식화할 수 있다.퍼즐의 불가능성은 3, 디스플레이 K_이 평면 그래프가 아니라는 사실에 합니다.이 불가능에 대한 여러 증거가 알려져 있으며, 두 개의 금지된 하위 그래프에 의해 평면 그래프를 특징짓는 쿠라토프스키 정리 증명의 일부를 형성한다. 그 중 는 3 K_이다.완전한 초당 그래프 도면에서 교차 횟수를 최소화하는 문제는 Turan의 벽돌 공장 프롤로 알려져 있다.em, K3,의 (\ K_ 최소 교차 횟수는 1회입니다.

3, 은 6개의 꼭지점과 9개의 모서리를 가진 그래프이며, [1]이 문제에 대해 흔히 유틸리티 그래프라고 합니다.그것은 또한 19세기 화학자 줄리어스 톰슨의 이름을 따서 톰슨 그래프로 불려왔다.잘 적용된 그래프, 가장 작은 삼각형 없는 입방 그래프 및 가장 작은 비평면 최소 강성 그래프입니다.

역사

세 가지 유틸리티 문제의 이력에 대한 검토는 Kullman(1979)에 의해 이루어졌다.그는 그 문제에 대한 대부분의 출판된 언급이 "매우 오래된"[2] 것으로 특징지어진다고 말한다.Kullman이 발견한 최초의 출판물에서 Henry Dudeney(1917)는 그것을 "물, 가스, 전기"라고 명명했다.그러나 Dudeney는 이 문제가 "언덕만큼 오래되었다"고 말한다.전등이나 가스보다 훨씬 오래됐어요.[3]Dudeney는 또한 1913년 [4]Strand Magazine에 같은 퍼즐을 발표했다.우선권에 대한 경쟁적인 주장은 그의 아들이 1900년에 [5]이 문제를 발표한 것으로 사후에 인용한 전기에서 인용한 샘 로이드에게 돌아간다.

이 문제의 또 다른 초기 버전은 세 채의 집을 세 개의 [6]우물에 연결하는 것이다.그것은 세 개의 집과 세 개의 분수가 모두 직사각형 벽에 닿아 있는 다른 (그리고 풀 수 있는) 퍼즐과 비슷하게 서술되어 있다; 퍼즐은 다시 교차하지 않는 연결을 만드는 것을 포함하지만, 현대의 숫자 링크 [7]퍼즐에서와 같이 지정된 세 쌍의 집과 우물 또는 분수 사이에서만 이루어진다.Loyd의 퍼즐 "The Rightsome Neighbors"는 비슷하게 세 개의 집을 세 개의 교차하지 않는 경로로 연결하는 것을 포함한다; 한 개의 집과 세 개의 문은 [8]다른 두 개의 집을 포함하는 직사각형 마당의 벽에 있다.

세 가지 유틸리티 문제뿐만 아니라 그래프[9][10] 강성에 대한 초기 연구와 화학 그래프 이론 모두에서 19세기 후반과 20세기 초에 출판되었습니다.여기서 줄리어스 톰슨은 1886년에 [11]벤젠의 불분명한 구조에 대해 그래프를 제안했습니다.톰슨의 업적을 기리기 위해 K, 3디스플레이 스타일 [12]을 톰슨 그래프라고 부르기도 합니다.

진술

3가지 유틸리티의 문제는 다음과 같습니다.

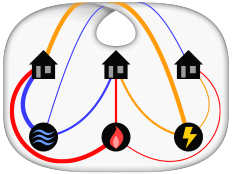
세 채의 집이 각각 수도, 가스 및 전기 회사에 연결되어야 하며, 각 집에서 각 회사까지 별도의 선을 사용해야 한다고 가정합니다.회선이 서로 교차하지 않고 9개의 접속을 모두 할 수 있는 방법이 있습니까?

문제는 실용적인 공학 상황에서는 존재하지 않는 제약을 가하는 추상적인 수학 퍼즐이다.그것의 수학적 공식화는 표면에 그래프를 삽입하는 것을 연구하는 위상 그래프 이론의 일부입니다.퍼즐의 중요한 부분이지만 종종 퍼즐의 비공식 단어에서 명확하게 언급되지 않는 부분은 집, 회사, 그리고 선들이 모두 평면의 토폴로지와 함께 2차원 표면에 배치되어야 하고, 선들이 다른 건물을 통과하지 못하게 해야 한다는 것입니다; 이것은 때때로 도면 O를 보여주면서 강제됩니다.f 집들과 회사들, 그리고 같은 [13][14]도면에 선으로 연결을 그리도록 요청합니다.

좀 더 형식적인 그래프 이론 용어로, 이 문제는 완전한 초당 K, 이 평면 그래프인지 여부를 묻습니다.이 그래프에는 각 주택에 대해 하나의 정점, 각 효용에 대해 하나의 정점 등 3개의 하위 집합 두 개에 6개의 정점이 있습니다.유틸리티가 있는 집의 각 쌍에 대해 하나의 가장자리, 또는 추상적으로 한 부분 집합의 정점과 다른 부분 집합의 정점의 각 쌍에 대해 하나의 가장자리인 9개의 모서리가 있습니다.평면 그래프는 평면에 교차하지 않고 그릴 수 있는 그래프이며, 그러한 도면을 찾을 수 있다면 세 가지 유틸리티 [13][14]퍼즐을 해결할 수 있을 것이다.

퍼즐 솔루션

분해 불능

단어 없는 증명:한 집은 일시적으로 삭제됩니다.나머지 주택과 공공시설을 연결하는 선은 평면을 세 지역으로 나눈다.삭제된 집이 어느 지역에 배치되어 있어도 마찬가지로 음영 처리된 유틸리티는 영역 밖에 있습니다.조던 곡선 정리에 따르면 이들을 연결하는 선은 기존 선 중 하나와 교차해야 한다.

통상적으로 (평탄한 2차원 평면상에서) 표시되기 때문에 유틸리티 퍼즐의 해답은 「아니오」입니다.즉, 9개의 모든 접속을 서로 교차하지 않고서는 할 수 없습니다.즉, , 3은 평면이 아닙니다.Kazimierz Kuratowski는 1930년에 은 [15]이며, 그 결과 이 문제는 해결 방법이 없다고 말했다.그러나 Kullman(1979)은 "흥미롭게도 쿠라토프스키가 [ ,3(\3,3})]가 비평면이라는 상세한 증거를 발표하지 않았다"[2]고 말한다.

3,의 을 찾을 수 없다는 증거 중 하나는 조던 곡선정리와 [16]관련된 사례 분석을 사용한다.이 솔루션에서는 그래프의 4주기와 관련하여 정점의 위치에 대한 다양한 가능성을 조사하고 모두 평면 [17]매립과 일관성이 없음을 보여준다.

오일러 V -+ \ V - F = 2 \ F= 2 \ F 2 \displaystyle 2 \- 의 브릿지 없는 초당 평면 그래프(\V - 를 가질 수 있다.평면 매립)의 경우 면의 수가 가장자리 수의 최대 절반(각 면 주변의 정점은 집과 유틸리티 사이를 번갈아 이동해야 하므로 각 면은 최소 4개의 모서리를 가지며 각 모서리는 정확히 2개의 면에 속함)이라는 관찰을 수반한다.효용 에서는 E (\) 및 V - 8(\8)이므로 효용 그래프에서는 E2 - 4(\E 2V-4가 [18]맞지 않으므로 평면이 될 수 없습니다.

규칙 변경

토러스 용액
뫼비우스 스트립의 솔루션

3, ({ K_은 트로이덜 그래프로,[19] 1속 표면인 토러스 위에 교차하지 않고 삽입할 수 있습니다.이러한 임베딩은 집과 회사가 평평한 [20]평면 대신 커피 머그나 다른 표면에 그려지는 퍼즐의 버전을 해결합니다.토러스에는 4개의 집과 [21][5]4개의 유틸리티로 퍼즐의 버전을 풀기에 충분한 자유도가 있다.마찬가지로 투명재료의 시트 위에 3개의 유틸리티 퍼즐을 제시하면 시트를 비틀어 접착한 후 풀 수 있어 뫼비우스 [22]스트립을 형성할 수 있다.

헨리 두데니가 제안한 퍼즐의 규칙을 푸는 또 다른 방법은 전력선이 연결된 [3]집이나 전력망을 통과하도록 하는 것이다.

유틸리티 그래프의 속성

유틸리티 퍼즐 이외에도 강성 이론, 케이지와 잘 덮인 그래프의 분류, 그래프 교차 수 연구, 그래프 부차자 이론을 포함한 여러 수학적 맥락에서 동일한 3, 이 나타난다.

강성

유틸리티 3, K_은 라만 그래프입니다. 즉, 평면 내의 거의 모든 정점의 위치에 대해 평면 전체의 강성 운동을 제외한 모든 가장자리 길이를 유지하면서 정점을 연속적으로 이동할 수 있는 방법은 없으며 스패닝 서브그래프는 동일한 강성을 가지지 않습니다.비평면 라만 [23]그래프의 가장 작은 예입니다.최소 강성 그래프임에도 불구하고 [9][24]정점에 특별한 배치를 가진 비강성 임베딩이 있습니다.일반 위치 임베딩의 경우, 동일한 에지 길이를 가진 모든 가능한 배치를 설명하는 다항식 방정식은 16도를 가지며, 이는 일반적으로 동일한 길이를 가진 최대 16개의 위치가 있을 수 있음을 의미합니다.이 방정식에 대한 최대 8개의 솔루션이 실현 가능한 [24]배치를 설명하는 가장자리 길이의 시스템을 찾을 수 있습니다.

기타 그래프 이론 속성

3, 은 삼각형이 없는 그래프이며, 각 정점에 정확히 3개의 인접 그래프(입방 그래프)가 있습니다.모든 그래프 중에서 가장 작은 그래프입니다.따라서 (3,4)-케이지입니다.이것은 정점당 3개의 네이버를 가지며 최단 사이클의 길이가 [25]4인 가장 작은 그래프입니다.

다른 모든 완전한 초당 그래프와 마찬가지로, 이 그래프는 잘 적용된 그래프이며, 즉 모든 최대 독립 집합의 크기가 동일하다는 것을 의미합니다.이 그래프에서 유일하게 두 개의 최대 독립 집합은 양당의 양면이며 크기가 같다.3,3 ({은 3개의 정규 3연결로 잘 커버된 [26]7개의 그래프 중 하나입니다.

일반화

3,의 (\3,3}})을 교차 1개로 표시

평면 그래프의 두 가지 중요한 특징인 Kuratowski의 정리, 평면 그래프는 정확히 도 완전한 도 포함하지 않는 그래프라는 바그너의 정리K3, ({ 스타일}}) 5 ({ K_{5는로서K 3, 3 스타일K_{3[27]의 비평면성을 사용하고 일반화한다.

팔 투란의 "벽돌 공장 문제"는 보다 일반적으로 완전한 초당 K (\b})의 그림에서 초당 양쪽에 있는 와b(\ b의 개수에 대한 공식을 요구한다.유틸리티 K, 3 K_은 1개의 교차로만 그릴 수 있지만 0의 교차로는 그릴 수 없으므로 교차 [5][28]번호는 1입니다.


레퍼런스

  1. ^ Gries, David; Schneider, Fred B. (1993), "Chapter 19: A theory of graphs", A Logical Approach to Discrete Math, New York: Springer, p. 423–460, doi:10.1007/978-1-4757-3837-7, ISBN 978-1-4419-2835-1, S2CID 206657798. 페이지 437 참조: ", 3은 유틸리티 그래프로 알려져 있습니다."
  2. ^ a b Kullman, David (1979), "The utilities problem", Mathematics Magazine, 52 (5): 299–302, doi:10.1080/0025570X.1979.11976807, JSTOR 2689782
  3. ^ a b Dudeney, Henry (1917), "Problem 251 – Water, Gas, and Electricity", Amusements in mathematics, vol. 100, Thomas Nelson, p. 73, Bibcode:1917Natur.100..302., doi:10.1038/100302a0, S2CID 10245524. 페이지 200-201에 제시된 해법은 다른 집들 중 하나를 통과하는 것을 포함한다.
  4. ^ Dudeney, Henry (1913), "Perplexities, with some easy puzzles for beginners", The Strand Magazine, vol. 46, p. 110
  5. ^ a b c Beineke, Lowell; Wilson, Robin (2010), "The early history of the brick factory problem", The Mathematical Intelligencer, 32 (2): 41–48, doi:10.1007/s00283-009-9120-4, MR 2657999, S2CID 122588849
  6. ^ "Puzzle", Successful Farming, vol. 13, p. 50, 1914; 를 참조해 주세요.
  7. ^ "32. The fountain puzzle", The Magician's Own Book, Or, The Whole Art of Conjuring, New York: Dick & Fitzgerald, 1857, p. 276
  8. ^ Loyd, Sam (1959), "82: The Quarrelsome Neighbors", in Gardner, Martin (ed.), Mathematical Puzzles of Sam Loyd, Dover Books, p. 79, ISBN 9780486204987
  9. ^ a b Dixon, A. C. (1899), "On certain deformable frameworks", Messenger of Mathematics, 29: 1–21, JFM 30.0622.02
  10. ^ 특히 페이지 403을 참조하십시오Henneberg, L. (1908), "Die graphische Statik der starren Körper", Encyklopädie der Mathematischen Wissenschaften, vol. 4, pp. 345–434.
  11. ^ Thomsen, Julius (July 1886), "Die Constitution des Benzols" (PDF), Berichte der Deutschen Chemischen Gesellschaft, 19 (2): 2944–2950, doi:10.1002/cber.188601902285
  12. ^ Bollobás, Béla (1998), Modern Graph Theory, Graduate Texts in Mathematics, vol. 184, Springer-Verlag, New York, p. 23, doi:10.1007/978-1-4612-0619-4, ISBN 0-387-98488-7, MR 1633290
  13. ^ a b Harary, Frank (1960), "Some historical and intuitive aspects of graph theory", SIAM Review, 2 (2): 123–131, Bibcode:1960SIAMR...2..123H, doi:10.1137/1002023, MR 0111698
  14. ^ a b Bóna, Miklós(2011년), AWalkCombinatorics을 통해:.도입된 열거형과 그래프 이론, 세계 과학,를 대신하여 서명함. 275–277, 아이 에스비엔 9789814335232.Bóna 우편 275에, 그리고"K3 내는 것의 문제에 3{\displaystyle 해당합니다 K_{3,3}}에서 비행기를 표면이 없는 건널목"페이지의 주 277에 쓴다 퍼즐(3주택의 세 우물과 연결될 수 있는)을 소개한다.
  15. ^ Kuratowski, Kazimierz (1930), "Sur le problème des courbes gauches en topologie" (PDF), Fundamenta Mathematicae (in French), 15: 271–283, doi:10.4064/fm-15-1-271-283
  16. ^ Ayres, W. L. (1938), "Some elementary aspects of topology", The American Mathematical Monthly, 45 (2): 88–92, doi:10.1080/00029890.1938.11990773, JSTOR 2304276, MR 1524194
  17. ^ Trudeau, Richard J. (1993), Introduction to Graph Theory, Dover Books on Mathematics, New York: Dover Publications, pp. 68–70, ISBN 978-0-486-67870-2
  18. ^ Kappraff, Jay (2001), Connections: The Geometric Bridge Between Art and Science, K & E Series on Knots and Everything, vol. 25, World Scientific, p. 128, ISBN 9789810245863
  19. ^ 페이지 409 참조Harary, F. (1964), "Recent results in topological graph theory", Acta Mathematica, 15 (3–4): 405–411, doi:10.1007/BF01897149, hdl:2027.42/41775, MR 0166775, S2CID 123170864.
  20. ^ Parker, Matt (2015), Things to Make and Do in the Fourth Dimension: A Mathematician's Journey Through Narcissistic Numbers, Optimal Dating Algorithms, at Least Two Kinds of Infinity, and More, New York: Farrar, Straus and Giroux, pp. 180–181, 191–192, ISBN 978-0-374-53563-6, MR 3753642
  21. ^ O’Beirne, T. H. (December 21, 1961), "Christmas puzzles and paradoxes, 51: For boys, men and heroes", New Scientist, vol. 12, no. 266, pp. 751–753
  22. ^ 라르센, Mogens 에스롬(1994년),"내 mazy 미로를 오해 나를 비참하게 할 수도 있", 가이, 리처드 K.;.는 외젠 Strens 기념관 회의 휴양 수학의 역사는 캘거리 대학, 캘거리 앨버타 주 8월 1986년, 합기도 스펙트럼, 워싱턴, DC에서 우드 로우, 로버트 E.(eds.), 논문집:수학 협회는 미국의,를 대신하여 서명함. 289–293, 아이 에스비엔 0-88385-516-X, MR1303141.페이지의 주 292개 그림 7참조하십시오.
  23. ^ 페이지 600 참조: "모든 것이 평면 그래프는 아니기 때문에 일반적으로 최소 강성 그래프에 의사 삼각관계로서 임베딩이 있는 것은 아니다Streinu, Ileana (2005), "Pseudo-triangulations, rigidity and motion planning", Discrete & Computational Geometry, 34 (4): 587–635, doi:10.1007/s00454-005-1184-0, MR 2173930, S2CID 25281202.가장 작은 예는 3, }})입니다.
  24. ^ a b Walter, D.; Husty, M. L. (2007), "On a nine-bar linkage, its possible configurations and conditions for paradoxical mobility" (PDF), in Merlet, Jean-Pierre; Dahan, Marc (eds.), 12th World Congress on Mechanism and Machine Science (IFToMM 2007), International Federation for the Promotion of Mechanism and Machine Science
  25. ^ Tutte, W. T. (1947), "A family of cubical graphs", Proceedings of the Cambridge Philosophical Society, 43 (4): 459–474, Bibcode:1947PCPS...43..459T, doi:10.1017/s0305004100023720, MR 0021678
  26. ^ Campbell, S. R.; Ellingham, M. N.; Royle, Gordon F. (1993), "A characterisation of well-covered cubic graphs", Journal of Combinatorial Mathematics and Combinatorial Computing, 13: 193–212, MR 1220613
  27. ^ Little, Charles H. C. (1976), "A theorem on planar graphs", in Casse, Louis R. A.; Wallis, Walter D. (eds.), Combinatorial Mathematics IV: Proceedings of the Fourth Australian Conference Held at the University of Adelaide August 27–29, 1975, Lecture Notes in Mathematics, vol. 560, Springer, pp. 136–141, doi:10.1007/BFb0097375, MR 0427121
  28. ^ Pach, János; Sharir, Micha (2009), "5.1 Crossings—the Brick Factory Problem", Combinatorial Geometry and Its Algorithmic Applications: The Alcalá Lectures, Mathematical Surveys and Monographs, vol. 152, American Mathematical Society, pp. 126–127

외부 링크