습식

습윤은 고체 표면과의 접촉을 유지하는 액체의 능력으로서, 두 가지가 합쳐질 때 분자간 상호작용에서 비롯된다.이것은 기체 위상이나 첫 번째 위상과 일치하지 않는 또 다른 액체 위상이 있을 때 발생한다.습식 정도(습식성)는 접착력과 응집력 사이의 힘의 균형에 의해 결정된다.

습윤은 두 재료의 결합이나 접착에 중요하다.^[1]습윤과 습윤을 제어하는 표면력 또한 모세관 효과를 포함한 다른 관련 효과의 원인이 된다.

습윤에는 비반응적 습윤과 반응적 습윤의 두 종류가 있다.^[2][3]

습윤은 가스, 액체, 고체의 세 단계를 다룬다.지난 20년간 많은 나노물질(그래핀,^[4] 탄소나노튜브, 질화 붕소나노메쉬^[5] 등)의 출현으로 현재 나노기술과 나노과학연구에서 주목받는 중심지로 자리 잡고 있다.

설명

액체와 고체 사이의 접착력은 액체 방울을 표면 전체에 퍼지게 한다.액체 내부의 응집력은 낙하물이 공 모양으로 부풀어 올라 표면과의 접촉을 피하게 한다.

그림 2	접촉각	정도 젖는	상호작용 강도
			고체-액체	액체-액체
S	θ = 0	완벽한 습식	강하다	약한
C	0 < θ < 90°	높은 습윤성	강하다	강하다
			약한	약한
B	90° ≤ θ < 180°	습도가 낮음	약한	강하다
A	θ = 180°	논웨팅	약한	강하다

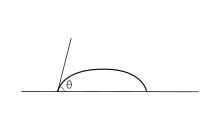
접촉 각도(θ)는 그림 1에서 보는 바와 같이 액체-증기 인터페이스가 고체-액체 인터페이스를 만족하는 각도다.접촉 각도는 접착력과 응집력 사이의 균형에 의해 결정된다.평평하고 단단한 표면에 넓게 퍼지는 낙하 경향이 증가함에 따라 접촉 각도가 감소한다.따라서 접촉 각도는 습윤성의 역 측정치를 제공한다.^[6]

접촉각(접점각)이 90°(접점각도가 낮음) 미만이면 일반적으로 표면의 습윤이 매우 유리하며, 액체가 표면의 넓은 면적에 퍼질 것이라는 것을 나타낸다.접촉각(높은 접촉각)은 일반적으로 표면의 습윤이 불리하므로 액체가 표면과의 접촉을 최소화하고 콤팩트한 액체 방울을 형성한다는 것을 의미한다.

물의 경우 습식 표면은 친수성 및 비습식 표면 친수성이라고도 할 수 있다.초저공포성 표면은 150° 이상의 접촉 각도를 가지며 액체 방울과 표면 사이에 거의 접촉이 없음을 보여준다.이것은 때때로 "로투스 효과"라고 불린다.표에는 다양한 접촉 각도와 그에 상응하는 고체/액체 및 액체/액체 상호작용이 설명되어 있다.^[7]물이 아닌 액체의 경우 낮은 접촉 각도 조건에 대해 라오필릭이라는 용어가 사용되며, 높은 접촉 각도가 발생할 때 라오필릭이라는 용어가 사용된다.마찬가지로, 전족공포증과 전족공포증이라는 용어는 극지방과 극지방 액체에 모두 적용된다.

고에너지 vs 저에너지 표면

액체는 두 가지 주요 유형의 고체 표면과 상호작용할 수 있다.전통적으로 고체 표면은 고에너지 고형분과 저에너지 고형분으로 구분되어 왔다.고체의 상대적 에너지는 고체 자체의 부피가 큰 성질과 관계가 있다.금속, 안경, 세라믹과 같은 고체는 이들을 한데 묶어주는 화학적 결합(예: 공밸런트, 이온성 또는 금속성)이 매우 강하기 때문에 '경질 고형물'로 알려져 있다.따라서 이러한 고형물을 깨는 데는 많은 양의 에너지가 필요하므로(대안적으로는 대량으로 잘라 두 개의 별도 표면을 만드는 데 많은 양의 에너지가 필요하다) 이를 "고형 에너지"라고 부른다.대부분의 분자 액체는 고에너지 표면으로 완전히 적신다.

다른 유형의 고체는 분자가 본질적으로 물리적인 힘(예: 반 데르 발스 힘과 수소 결합)에 의해 결합되는 약한 분자 결정(예: 플루오르화탄소, 탄화수소 등)이다.이러한 고형물은 약한 힘에 의해 함께 고정되기 때문에 이를 깨는 데 매우 적은 양의 에너지가 필요하므로 이를 "저 에너지"라고 부른다.선택한 액체의 종류에 따라 저에너지 표면은 완전 또는 부분적 습윤을 허용할 수 있다.^[8][9]

동적 표면은 적절한 자극의 적용에 따라 표면 에너지의 변화를 겪는 것으로 보고되었다.예를 들어 광자 구동 분자 모터를 표시하는 표면은 서로 다른 표면 에너지의 비스트 가능 순응 사이에서 전환할 때 물 접촉 각도의 변화를 겪는 것으로 나타났다.^[10]

저에너지 표면의 습윤

저에너지 표면은 주로 분산력(van der Waals)의 힘을 통해 액체와 상호작용한다.William Zisman은 다음과 같은 몇 가지 주요 결과를 도출했다.^[11]

지스만은 cos θ이 액체의 표면장력(γ_LV)이 감소함에 따라 선형적으로 증가한다고 관찰했다.따라서 그는 각종 유기액에 대한 cos and과 표면장력(surface tension, surface_LV tension, surface tension) 사이의 선형함수를 확립할 수 있었다.

표면은_LV and과 low이 낮을 때 더 촉촉하다.지스만은 cos cos = 1일 때 이 선들의 절편을 그 표면의 임계 표면 장력(γ力_c)이라고 불렀다.이 임계 표면 장력은 고체의 특징이기 때문에 중요한 변수다.

고체의 임계 표면 장력을 알면 표면의 습윤성을 예측할 수 있다.^[6]표면의 습윤성은 고체의 가장 바깥쪽 화학 그룹에 의해 결정된다.구조가 비슷한 표면들 간의 습윤성의 차이는 원자의 패킹의 차이 때문이다.예를 들어, 만약 표면이 갈린 체인을 가지고 있다면, 그것은 직선 체인을 가진 표면보다 더 나쁜 패킹을 가질 것이다.임계 표면 장력이 낮다는 것은 습식 가능한 재료 표면을 의미한다.

이상적인 솔리드 표면

이상적인 표면은 평평하고 견고하며 완벽히 매끄럽고 화학적으로 균일하며 접촉각 이력(zero contact angle hysteresis)이 없다.제로 이력(zero hysteresis)은 전진하는 접촉각과 후퇴하는 접촉각이 동일하다는 것을 의미한다.즉 열역학적으로 안정된 접촉각은 하나만 존재한다.액체 방울을 그러한 표면에 놓을 때, 특성 접촉 각도는 그림 1과 같이 형성된다.게다가 이상적인 표면에서는, 만약 그것이 방해된다면, 그 방울은 원래의 모습으로 되돌아갈 것이다.^[7][11]다음의 파생은 이상적인 고체 표면에만 적용된다; 그것들은 인터페이스가 움직이지 않고 위상 경계선이 평형상태로 존재하는 상태에만 유효하다.

에너지 최소화, 3상

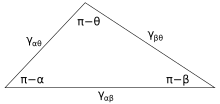
그림 3은 3상이 만나는 접촉선을 나타낸다.평형에서 3상 사이의 경계선을 따라 작용하는 단위 길이당 순력은 0이어야 한다.각 인터페이스를 따라 방향에서 순방향 힘의 구성요소는 다음과 같이 주어진다.

${\displaystyle{\begin{정렬}\gamma _{\alpha \theta}+\gamma _{\beta\theta}\cos \left(\theta \right)+\gamma _{\alpha \beta}\cos \left(\alpha \right)&,=0\\\gamma _{\alpha \theta}\cos _{\beta\theta}+\gamma _{\alpha \beta}\cos \left(\beta \right)& \left(\theta \right)+\gamma,=0\\\gamma _{\alpha \theta}\cos \left(\alpha \right)+\gamma다.{\theta\cHB \cos \left(\reft \right)+\reft _{\required}{\required}}}$

여기서 α, β, θ은 표시된 각도, γ은_ij 표시된 두 단계 사이의 표면 에너지다.이러한 관계는 그림 4에 나타낸 것과 같이 노이만의 삼각형이라고 알려진 삼각형과 유사하게 표현될 수도 있다.노이만의 삼각형은 $\alpha {\displaystyle }$ +${\displaystyle \beta }$ +${\displaystyle \alpha }$ =${\displaystyle \mathrm{\beta }}$ = π = 2 ${\displaystyle \pi }$ ${\displaystyle \alpha +\beta +\theta =2\pi$의 기하학적 제한과 일치하며, 여기에 사인 법칙과 코사인 법칙을 적용하여 인터페이스 각도가 표면 에너지의 비율에 어떻게 의존하는지를 기술하는 관계를 생산한다.^[12]

이 세 가지 표면 에너지는 삼각형의 측면을 형성하기 때문에, 그들은 삼각형 불평등, surface_ij < γ_jk + γ에_ik 의해 제약을 받기 때문에, 표면의 긴장 중 어떤 것도 다른 두 개의 합을 초과할 수 없다는 것을 의미한다.이러한 불평등을 따르지 않는 표면 에너지를 가진 3개의 유체가 접촉한다면, 그림 3과 일치하는 평형 구성은 존재하지 않을 것이다.

평면 기하학의 단순화, 영의 관계

그림 5와 같이 β 위상을 평평한 강체 표면으로 대체하면 β = β, 두 번째 순힘 방정식이 영 방정식으로 단순화된다.^[13]

${\displaystyle \gamma _{SG}=\gamma _{SL}+\gamma _{LG}\coses \left(\theta \right)}$^[14]

그것은 고체, 액체, 기체의 세 단계 사이의 표면 장력과 관련이 있다.이후, 이것은 관련된 세 가지 표면 에너지에 대한 지식으로부터 고체 표면의 액체 방울의 접촉 각도를 예측한다.이 방정식은 또한 "가스" 단계가 첫 번째 "액체" 단계의 방울과 함께 다른 액체인 경우에도 적용된다.

가변적 계산에서 도출된 Young의 관계인 평면 기하학과의 단순화

$L{\displaystyle }$ ${\displaystyle L}$이(가) 사용 가능한 매개 변수인$$ $경우$ x ${\displaystyle \in }$ I${\displaystyle }$=${\displaystyle }$[ ${\displaystyle 0,}$ ${\displaystyle \mathrm{L}}$ ${\displaystyle ]}$ ${\displaystyle x\in$ I$=[0,L]}$의 경우 $인터페이스$를 곡선 y${\displaystyle (x}$ ${\displaystyle )}${\$displaysty$ y$(x)}$으로 간주하십시오.최소화할 자유 에너지는

${\displaystyle {\cal{F}}=\int _{0}^{L}\왼쪽(\gamma _{LG}{\sqrt{1+y'^{2}}+(\gamma _{SL}-\SG}\오른쪽)dx}$

$제한조건{\displaystyle y}$(${\displaystyle 0}$ )${\displaystyle }$= y${\displaystyle }$( L )${\displaystyle }$= 0$${\$displaystyle y$ $(0)=y($L)=$0}$을(를) 사용하여 $\int {\displaystyle {}_{}}$ ${\displaystyle {}_{}{}^{}}$ ${\displaystyle {\prime }^{}}$ ${\displaystyle d}$ ${\displaystyle x}$= ${\displaystyle 0}$ ${\displaysty \int _{$$I}$$y'dx=0}$ 및 고정 볼륨$$ ${\displaystyle \mathrm{volume}}{\displaystyle {}_{}}$I ${\displaystyle {}_{}}$= ${\displaystyle A}$ ${\displaystysty \int \int _A$

따라서 제약 조건을 고려하여 수정된 라그랑지아인은

${\displaystyle {\cal{L}=\gamma _{{LG}{\sqrt{1+y'^{2}}+(\gamma _{SL}-\lambda _{1}-\lambda _{2}y})$

여기서 $\lambda {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$는 라그랑주 승수다.정의상 모멘텀 ${\displaystyle {p{}^{}}_{}}$= ${\displaystyle {{\partial }^{}}_{}}$ y ${\$'}{\$cal{L},$ $해밀턴$ H${\displaystyle }$= p ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$- ${\displaystyle L\mathcal{}}$ ${\$ {\$h}=py'-{\cal}}}}$는 다음과 같이 계산된다$$.

${\displaystyle {\cal{H}=-\gamma _{LG}{1}{1}{1\sqrt{1+y'^{2}}-(\gamma_{SL}-\gamma_{SG}+\lambda _{2}y}}$

이제 $경계$가 x ${\displaystyle$ x}$방향$으로 자유롭고$$ $L{\displaystyle }$ ${\displaystyle$ L$}$이(가) 자유 매개 변수임을$$ 상기한다.따라서 다음을 충족해야 한다.

${\displaystyle {\frac {\cal {F}{\partial L}=-{\cal {H}=0}$

${\displaystyle \mathrm{경계}}$ $y{\displaystyle }$( ${\displaystyle L}$)${\displaystyle }$= 0 ${\displaystyle$ y$($${\displaystyle \mathrm{L}}$$)=0}$ 및$$${\displaystyle }$( ${\displaystyle {1\mathrm{}}^{}}$+ ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ 2${\displaystyle {}^{}{}^{}}$)${\displaystyle {}^{}}$- 1${\displaystyle {}^{}}$/ ${\displaystyle {2\mathrm{}}^{}}$= ${\displaystyle \cos }$ ${\displaystyle }$ ⁡ $\$ {\$displaystyle (1+y$'^{$2}^{-1/2}=\cos \teta$ 따라서 영 방정식을 복구한다.

비이상적인 매끄러운 표면 및 젊은 접촉 각도

Young 방정식은 이상적인 표면으로 종종 언급되는 완벽하게 평평하고 단단한 표면을 가정한다.많은 경우에 표면은 이러한 이상적인 상황과 거리가 멀며, 여기에서 두 가지, 즉 거친 표면의 경우와 아직 실제적인 매끄러운 표면의 경우(완전히 강직함)가 고려된다.완벽하게 매끄러운 표면에서도 낙하물은 소위 전진하는 ${\displaystyle {접촉각}_{}}$인 , $A{\displaystyle {}_{}}$ ${\$부터 소위 후퇴하는 $접촉각$인 { ${\displaystyle {R\mathrm{}}_{}}$ ${\$에 이르는 광범위한 접촉각 스펙트럼을 가정할 것이다$.$평형 접점 각도(${\displaystyle {}_{}}$ ${\displaystyle {c\mathrm{}}_{}}${\$displaystyle \theta _$${\mathrm{c$$\}\}\})$는 Tadmor가^[15] 나타낸 것과$$ 같이 ${\displaystyle {a\mathrm{}}_{}}$ ${\displaystyle {A\mathrm{}}_{}}$${\$$$\$theta \{\mathrm${R$}}$에서 계산할 수 있다.

${\displaystyle \theta _{\mathrm {c} }=\arccos \left({\frac {r_{\mathrm {A} }\cos \left(\theta _{\mathrm {A} }\right)+r_{\mathrm {R} }\cos \left(\theta _{\mathrm {R} }\right)}{r_{\mathrm {A} }+r_{\mathrm {R} }}}\right)}$

어디에

${\displaystyle r_{\mathrm {A} }=\left({\frac {\sin ^{3}\left(\theta _{\mathrm {A} }\right)}{2-3\cos \left(\theta _{\mathrm {A} }\right)+\cos ^{3}\left(\theta _{\mathrm {A} }\right)}}\right)^{\frac {1}{3}}~;~~r_{\mathrm {R} }=\left({\frac {\sin ^{3}\left(\theta _{\mathrm {R} }\right)}{2-3\cos \left(\theta _{\mathrm {R} }\right)+\cos ^{3}\left(\theta_{\mathrm {R} }\오른쪽)^{\frac{1}{3}}}$

영-듀프레 방정식과 확산 계수

영-듀프레 방정식(토마스 영 1805; 안타나세 뒤프레와 폴 뒤프레 1869)은 neither과_SG γ은_SL 다른 두 표면 에너지의 합보다 클 수 없다고 지시한다.^[16][17]이 제한의 결과는 γ_SGSL > γ_SL + γ일_LG 때 완전 습윤을_SG 예측하고, when > γ_LG + γ일 때 영 습윤을 예측하는 것이다.영-듀프레 방정식에 대한 해결책이 없다는 것은 그러한 상황에 대해 접점 각도가 0~180°인 평형 구성이 없다는 것을 보여주는 지표다.^[18]

습식 측정의 유용한 매개변수는 확산 매개변수 S,

${\displaystyle S=\gamma _{SG}-\왼쪽(\gamma _{SL}+\gamma _{LG}\오른쪽)}$

S > 0일 때 액체는 표면을 완전히 적신다(완전 습식).S < 0일 때 부분적 습윤이 발생한다.

확산 매개변수 정의와 젊은 관계를 결합하면 영-듀프레 방정식이 도출된다.

${\displaystyle S=\gamma _{LG}\left(\cos \left(\theta \right)-1\right)}$

S < 0일 때 θ에 대한 물리적 해결책만 가지고 있다.

습식 계산 예측

많은 표면/어드밴티지 구성의 경우, 표면 에너지 데이터와 실험 관측치를 사용할 수 없다.습식 상호작용은 다양한 용도에서 매우 중요하므로, 물이나 다른 흡착물과 관련하여 특정 결정학적 방향과 함께 다양한 재료 표면의 습식 동작을 예측하고 비교하는 것이 종종 바람직하다.이것은 분자 역학 및 밀도 기능 이론을 포함한 도구로 원자론적 관점에서 이루어질 수 있다.^[19][20]DFT와 같은 아비니시오 접근법에 의한 습윤의 이론적 예측에서 얼음은 일반적으로 물로 대체된다.이는 DFT 계산이 일반적으로 원자의 열 이동 제로 조건을 가정하여 수행되기 때문이며, 이는 본질적으로 시뮬레이션이 절대 0에서 수행된다는 것을 의미한다.그럼에도 불구하고 이러한 단순화는 현실적 조건 하에서 물의 흡착과 관련된 결과를 산출하며 습윤의 이론적 시뮬레이션을 위한 얼음의 사용은 일반적이다.^[21]

비이상적인 거친 고형 표면

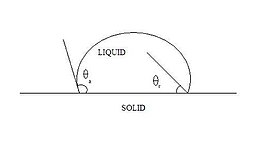
이상적인 표면과는 달리 실제 표면은 완벽한 부드러움, 강직성 또는 화학적 동질성을 가지고 있지 않다.이상성으로부터의 그러한 편차는 접촉각 이력이라고 불리는 현상을 초래하는데, 이는 전진(진행_a)과 후퇴(진행_r) 접촉각의^[22] 차이로 정의된다.

${\displaystyle {\text{H}}=\,\theta _{a}-\,\theta _{r}}}$

접촉 각도가 전진 및 후퇴 케이스 사이에 있는 경우 접촉 라인이 핀으로 고정된 것으로 간주되며 이력거동, 즉 접촉 각도 이력(contact angle hysteresis)을 관찰할 수 있다.이러한 값을 초과할 경우, 그림 3의 것과 같은 접촉 선의 변위는 방울의 팽창 또는 수축에 의해 이루어진다.^[23]그림 6은 전진 및 후퇴하는 접촉 각도를 나타낸다.전진하는 접촉각은 최대 안정각인 반면 후퇴하는 접촉각은 최소 안정각이다.접촉각 이력(contact angle hysteresis)은 비이상 고형에서 열역학적으로 안정적인 접촉 각도가 많이 발견되기 때문에 발생한다.이렇게 변화하는 열역학적으로 안정적인 접촉 각도를 측정 가능한 상태로 알려져 있다.^[11]

그러한 위상 경계의 움직임은, 전진하고 후퇴하는 접촉 각도를 포함하는 것으로, 동적 습윤이라고 알려져 있다.동적 습윤각과 정적 습윤각의 차이는 모세관 번호 $C{\displaystyle }$ ${\displaystyle a}$ ${\displaystyle Ca}$에 비례하며$,$ 접촉선이 진행되어 표면의 더 많은 부분을 액체로 덮으면 접촉각이 증가하며 일반적으로 접촉선의 속도와 관련이 있다.^[23][24]접촉선의 속도가 제한 없이 증가하면 접촉각이 증가하며, 180°에 가까워질수록 기체 위상은 액체와 고체 사이의 얇은 층에 막히게 된다.이것은 접촉선이 완전히 젖을 수 없을 정도로 빠른 속도로 이동하면서 발생하는 운동적 불균형 효과다.

이상적인 조건으로부터의 잘 알려진 이탈은 관심의 표면이 거친 질감을 가질 때 이다.표면의 거친 질감은 동종 또는 이종의 두 가지 범주 중 하나로 분류될 수 있다.균질하게 적시는 체제는 액체가 거친 표면의 홈을 채우는 것이다.그러나 이질적인 습식 체제는 표면이 두 가지 유형의 패치로 이루어진 복합체인 곳이다.그러한 복합 표면의 중요한 예는 공기와 고체의 조각으로 구성된 것이다.그러한 표면은 젖은 액체의 접촉 각도에 다양한 영향을 미친다.캐시-백스터와 웬젤은 질감 있는 표면의 습윤을 설명하려는 두 가지 주요 모델이다.그러나 이러한 방정식은 표면 거칠기 척도와 비교하여 낙하 크기가 충분히 큰 경우에만 적용된다.^[25]물방울 크기가 밑줄과 비교될 때 라인 장력의 영향을 고려해야 한다.^[26]

원젤의 모델

Wenzel 모델(Robert N).Wenzel, 1936년)은 그림 7에서 보는 것과 같은 균질 습식 체제를 설명하며, 거친 표면의 접촉 각도에 대해 다음과 같은 방정식으로 정의된다.^[25]

${\displaystyle \cos \,\좌(\theta ^{*}\우)=r\cos \,\좌(\theta \우)}$

여기서 ${\$는 안정된 평형 상태(즉, 시스템의 최소 자유 에너지 상태)에 해당하는 명백한 접촉각이다$$.거칠기 비율 r은 표면 거칠기가 동질 표면에 어떤 영향을 미치는지 나타내는 척도다.거칠기 비율은 표면적에 대한 고체 표면의 실제 면적의 비율로 정의된다.

θ은 이상적인 표면에 대해 정의된 Young 접촉각이다.비록 Wenzel의 방정식은 거친 표면의 접촉 각도가 본질적인 접촉 각도와 다르다는 것을 보여주지만, 접촉 각도 이력은 설명하지 않는다.^[27]

캐시-백스터 모델

이질적인 표면을 다룰 때 Wenzel 모델은 충분하지 않다.다양한 소재가 관련되었을 때 겉보기 접촉 각도가 어떻게 변화하는지 측정하기 위해서는 좀 더 복잡한 모델이 필요하다.그림 8에서 보는 것과 같은 이질적인 표면은 캐시-백스터 방정식(카시의 법칙)을 사용하여 설명된다.^[25]

${\displaystyle \cos \,\left(\theta ^{*}\right)=r_{f}\,f\,\cos \,\theta _{\text}Y}\오른쪽)+f-1}$

여기서 r은_f 습윤 표면적의 거칠기 비율이며 f는 액체에 의해 습윤된 고체 표면적의 비율이다.f = 1과 r_f = r이 되면 캐시-백스터 방정식이 Wenzel 방정식이 된다는 것을 깨닫는 것이 중요하다.한편, 표면 거칠기의 분율이 서로 다르면, 전체 표면적의 각 $부분$은 f ${\$로 표시된다$.$

모든 $f{\displaystyle {}_{}}$ ${\$의 합은 1 또는 전체 표면과 같다$$.캐시-백스터는 다음과 같은 방정식으로도 재작성할 수 있다.^[28]

${\displaystyle \gamma \cos \,\왼쪽(\theta ^{*}\오른쪽)=\sum _{n}f_{{n1}^{n}\i}\lf(\gamma _\text{i,sv}-\gamma_{\text{i,sl}\ri}\rigma}\오른쪽)}}}$

여기서 ${\displaystyle \gamma }$는 액체와 증기 사이의 캐시-백스터 표면 장력이고, ${\displaystyle i_{}}$ i${\displaystyle {}_{}}$, ${\displaystyle s_{}}$ v$${\$displaystyle \gamma$ $_$${i,sv}$는 모든 성분의 고체 증기 표면 장력이고, ${\displaystyle i_{}}$i , ${\displaystyle s_{}}$ ${\$은 모든$$ 성분의 고체 액체 표면 장력이다.언급할 가치가 있는 경우는 액체 방울을 기판 위에 놓고 그 밑에 작은 공기 주머니를 만들 때 입니다.2개 구성 요소 시스템의 경우 다음과 같이 표시된다.^[28]

${\displaystyle \cos \cos \,\lft(\theta ^{*}\오른쪽)=f_{1}\ft(\reft)\ft(\text{1,167}-\reft)({1-f_{1}\right)\put }}$

여기서 주목해야 할 주요 차이점은 두 번째 표면 장력 구성 요소에 대한 고체와 증기 사이에 표면 장력이 없다는 것이다.이는 노출된 공기의 표면이 방울 아래에 있고, 시스템에서 유일한 다른 기질이라는 가정 때문이다.이후 방정식은 (1 – f)로 표현된다.따라서 캐시 방정식은 캐시-백스터 방정식에서 쉽게 도출할 수 있다.Wenzel 대 Cassie-Baxter 시스템의 표면 특성에 관한 실험 결과는 Cassie-Baxter 모델에 따라 분류된 지역인 180~90°의 Young 각도를 고정하는 효과를 보여주었다.이 액상/공기 복합 시스템은 대부분 소수성을 띤다.그 지점 이후 낙하물이 표면을 찌르는 곳에서 원젤 정권으로의 급격한 전환이 발견되었지만 낙하 가장자리 이상은 아니었다.사실, 영, 웬젤, 캐시 백스터 방정식은 젖는 다양한 문제의 횡단성 조건을 나타낸다.^[29][30]

전구 영화

고해상도 이미징의 출현과 함께, 연구자들은 명백한 접촉 각도를 계산할 때 캐시-백스터 방정식의 가정에 의문을 제기하는 실험 데이터를 얻기 시작했다.이 그룹들은^[who?] 겉보기 접촉 각도가 크게 3중선에 의존한다고 믿는다.이질적인 표면과 맞닿아 있는 트리플 라인은 나머지 낙하물처럼 이질적인 표면에 쉴 수 없다.이론적으로는 표면의 불완전함을 따라야 한다.트리플 라인의 이러한 굴곡은 불리하며 실제 상황에서는 볼 수 없다.캐시-백스터 방정식을 보존함과 동시에 삼중 라인의 최소 에너지 상태의 존재를 설명하는 이론은 전구 필름의 아이디어에 달려 있다.이 서브마이크로미터 두께의 필름은 방울의 움직임보다 먼저 진행되며, 트리플 라인 주변에서 발견된다.나아가 이 전구영화는 트리플 라인이 구부러지고 원래 불리하다고 여겨졌던 다른 순응을 취할 수 있게 한다.이 전구체는 대량으로 모공이 형성된 표면에서 환경 스캐닝 전자 현미경(ESEM)을 사용하여 관찰되었다.전구 필름 개념의 도입으로, 트리플 라인은 활기차게 실현 가능한 순응을 따를 수 있으며, 따라서 캐시-백스터 모델을 정확하게 설명할 수 있다.^[31]

꽃잎 효과 vs."파워 효과"

표면의 고유 친수성은 다른 길이의 거칠기로 질감 처리됨으로써 강화될 수 있다.붉은 장미는 각각의 꽃잎에 있는 미세구조와 나노구조물의 위계를 이용하여 초저하증(superhrophobic)에 충분한 거칠기를 제공한다.좀 더 구체적으로 말하면, 각각의 장미 꽃잎은 표면에 마이크로파필레이의 컬렉션을 가지고 있고, 각 파피야는 차례로 많은 나노폴드를 가지고 있다.꽃잎 효과(petal effect)라는 용어는 장미 꽃잎 표면의 물방울 모양이 구형이지만 꽃잎이 뒤집혀도 굴러 떨어질 수 없다는 사실을 기술하고 있다.물방울은 꽃잎의 초강하성(접점각 약 152.4°)으로 인해 구형 형태를 유지하지만 꽃잎 표면은 물과 높은 접착력을 가지고 있기 때문에 굴러 떨어지지는 않는다.^[32]

" 꽃잎 효과"를 "로투스 효과"와 비교할 때, 눈에 띄는 몇 가지 차이점을 주목하는 것이 중요하다.그림 9와 같이 연잎과 장미 꽃잎의 표면 구조를 사용하여 두 가지 효과를 설명할 수 있다.

연잎은 표면이 무작위로 거칠고 접촉각 이력(hysteresis)이 적어 물방울이 송곳간 미세구조 공간을 적시지 못한다는 뜻이다.이것은 공기가 질감 안에 머물게 하여 공기와 고체로 구성된 이질적인 표면을 유발한다.그 결과 물과 고체 표면 사이의 접착력이 극히 낮아 물이 쉽게 굴러 떨어질 수 있다(즉, '셀프 세정' 현상).

장미 꽃잎의 미세 구조와 나노 구조는 연잎 구조보다 규모가 커서 액막이 질감을 담글 수 있다.그러나 그림 9에서 보는 바와 같이 액체는 더 큰 규모의 홈으로 들어갈 수 있지만 더 작은 홈으로 들어갈 수는 없다.이것은 캐시의 침윤식 습윤제라고 알려져 있다.액체가 큰 홈을 적실 수 있기 때문에 물과 고체 사이의 접착력이 매우 높다.꽃잎을 비스듬히 기울이거나 뒤집어도 물방울이 떨어지지 않는 이유가 여기에 있다.무게와 표면 장력 사이의 균형을 초과하기 때문에 방울의 부피가 10µl 이상이면 이 효과는 실패할 것이다.^[33]

캐시-백스터-웬젤 전환

캐시-백스터 모델에서, 그 방울은 질감 있는 표면 위에 있고 아래에 공기가 갇혀 있다.캐시 상태에서 웬젤 상태로 습식 전환이 진행되는 동안 에어 포켓은 더 이상 열역학적으로 안정적이지 않고 낙하 중간부터 액체가 핵화되기 시작하여 그림 10과 같이 "무스룸 상태"가 생성된다.^[34]관통 조건은 다음과 같이 주어진다.

${\displaystyle \cos \,\left(\theta _{\text{C}\right)={\fract {\phi -1}{r-\phi }}}$

어디에

• θ은_C 임계 접촉 각도
• φ은 강하가 표면과 접촉하는 고체/액체 인터페이스의 분율이다.
• r은 고체 거칠기(평탄한 표면의 경우, r = 1)

관통 전선은 낙하 가장자리에 도달할 때까지 표면 에너지를 최소화하기 위해 전파되어 원젤 상태에 도달한다.고체는 표면이 거칠기 때문에 흡수성 물질로 간주될 수 있기 때문에 이러한 확산과 임비션 현상을 헤미위킹이라고 한다.퍼짐/임비전이 발생하는 접점 각도는 0과 //2이다.^[35]

Wenzel 모델은 θ과_C 2/2 사이에 유효하다.접촉 각도가 θ_C 미만일 경우 투과전선이 낙하물 너머까지 퍼져나가 표면 위로 액막이 형성된다.그림 11은 원젤 상태에서 표면 필름 상태로의 전환을 그리고 있다.이 필름은 표면의 거칠기를 부드럽게 하고 Wenzel 모델은 더 이상 적용되지 않는다.이 상태에서 평형 조건과 영의 관계는 다음과 같이 산출된다.

${\displaystyle \cos \,\left(\theta ^{*}\오른쪽)=\phi \cos \cos \,\reft(\theta _{C}\right)+\reft(1-\phi \오른쪽)}$^[34]

표면의 거칠기를 미세하게 조정함으로써 초저공포증과 초저공포성 지역 간의 전환을 달성할 수 있다.일반적으로 표면이 거칠수록 소수성이 강하다.

확산 역학

한 방울을 매끄럽고 수평적인 표면에 놓으면 일반적으로 평형 상태가 아니다.따라서 평형 접촉 반경에 도달할 때까지(부분 습식) 확산된다.모세관, 중력, 점성 기여도를 고려하면서 시간의 함수로써 낙하 반경을 표현할^[36] 수 있다.

${\displaystyle r(t)=r_{e}\left[1-\exp \left(-\left({\frac {2\gamma _{LG}}{r_{e}^{12}}}+{\frac {\rho g}{9r_{e}^{10}}}\right){\frac {24\lambda V^{4}\left(t+t_{0}\right)}{\pi ^{2}\eta }}\right)\right]^{\frac {1}{6}}}$

완전한 습윤 상황을 위해, 확산 과정 중 언제든지 낙하 반경은 다음에 의해 주어진다.

${\displaystyle r(t)=\left[\left(\gamma _{LG}{\frac {96\lambda V^{4}}{\pi ^{2}\eta }}\left(t+t_{0}\right)\right)^{\frac {1}{2}}+\left({\frac {\lambda (t+t_{0})}{\eta }}\right)^{\frac {2}{3}}{\frac {24\rho gV^{\frac {3}{8}}}{7\cdot 96^{\frac {1}{3}}\pi ^{\frac {4}{3}}\gamma _{LG}^{\frac {1}{3}}}}\right]^{\frac {1}{6}}}$

어디에

• γ_LG 유체의 표면 장력
• V는 드롭 볼륨
• η 유체의 점성
• ρ은 유체의 밀도
• g는 중력 상수다.
• λ은 형상계수, 37.1 m이다⁻¹.
• t는₀ 실험 지연 시간이다.
• r은_e 평형 낙하 반지름이다.

습식 특성 수정

계면활성제

많은 기술적 과정들은 고체 표면 위로 액체가 퍼지는 통제를 필요로 한다.한 방울을 표면에 놓으면 완전히 젖거나 부분적으로 젖거나 또는 표면이 젖지 않을 수 있다.계면활성제로 표면 장력을 줄임으로써 비보팅 소재를 부분적으로 또는 완전히 적셔지게 할 수 있다.고체 표면에서 떨어지는 낙하물의 초과 자유 에너지(초과)는 다음과 같다.^[37]

${\displaystyle \sigma =\gamma S+PV+\pi \,R^{2}\왼쪽(\gamma _{\text}SL}-\gamma _{\text{SV}\오른쪽)}$

• γ은 액체-간격 장력이다.
• γ은_SL 고체-간격장력이다.
• γ은_SV 고체-간격장력이다.
• S는 액체-증기 인터페이스 영역이다.
• P는 액체 내부의 과도한 압력이다.
• R은 드롭릿 베이스의 반지름이다.

이 방정식을 바탕으로 γ이 감소하거나 γ이_SL 감소하거나 γ이_SV 증가하면 초과 자유에너지가 최소화된다.계면활성제는 액체-증기, 고체-액체, 고체-증기 인터페이스에 흡수되며, 이 인터페이스는 자유 에너지를 줄이기 위해 소수성 물질의 습윤 동작을 수정한다.계면활성제가 소수성 표면에 흡수되면, 극성 머리 그룹은 꼬리를 바깥쪽으로 향하게 하여 용액을 향한다.더 많은 소수성 표면에서 계면활성제는 고체에 빌레이어를 형성하여 고체가 더 친수성을 띠게 할 수 있다.동적 낙하 반경은 낙하물이 퍼지기 시작하면서 특징지어질 수 있다.따라서 다음과 같은 방정식에 따라 접촉 각도가 변한다.^[37]

${\displaystyle \cos \,\left(\theta (t)\right)=\cos \,\left(\theta _{0}\right)+\left(\cos \,\left(\theta _{\infty }\right)-\cos \,\left(\theta _{0}\right)\right)\left(1-\mathrm {e} ^{-{\frac {t}{\tau }}}\right)}$

• θ은₀ 초기 접촉 각도
• θ은_∞ 최종 접촉 각도
• τ 계면활성제 전달시간 척도

계면활성제가 흡수되면 고체-증기 표면 장력이 증가하고 낙하 가장자리는 친수성이 된다.그 결과 낙폭이 확산된다.

표면 변경

페로센은 리독스-능동 유기측정^[39] 화합물로 다양한 모노머에 통합될 수 있으며 표면에 테더링할 수 있는 폴리머를 만드는 데 사용된다.^[38]비니엘프로세르로센(페로세네일테네)은 위티그 반응에^[40] 의해 준비되고 중합되어 폴리스티렌의 아날로그인 폴리비닐프로센(PVFC)을 형성할 수 있다.형성될 수 있는 또 다른 폴리머는 PFCMA(2-(메타크릴로일록시) 에틸페로센카르복실산염), PFCMA이다. PVFc와 PFcMA는 모두 실리카 웨이퍼에 묶여 있으며, 폴리머 체인이 충전되지 않은 경우와 페로센 모이에가 산화되어 양전하 그룹이 생성될 때 측정된다.^[38]PFcMA 코팅 웨이퍼의 물과의 접촉 각도는 산화 후 70° 더 작았고, PVFc의 경우 감소는 30°였으며 습식성의 전환은 가역성이 있는 것으로 나타났다.PFcMA의 경우, 더 많은 페로센 그룹(그리고 더 큰 어금니 질량)을 가진 더 긴 체인의 효과가 조사되었고, 더 긴 체인은 훨씬 더 큰 접촉 각도 감소를 생성하는 것으로 밝혀졌다.^[38][41]

산소결핍

희토류 산화물에는 고유 친수성(hydrophobity)이 나타나므로 열안정적인 열교환기와 고온수질성(hydrophobity)을 수반하는 기타 용도에 사용할 수 있다.^[42]세리아나 다른 희토류 산화물 표면에서 산소결실의 존재는 표면 습윤성을 관리하는 데 중요한 역할을 한다.옥사이드 표면에서 물의 흡착은 HO₂ 분자가 종료된 표면에서 온전하게 유지되는 분자 흡착 또는 OH와 H를 고체 표면에서 별도로^[43] 흡착하는 분자 흡착으로 발생할 수 있다.산소결핍의 존재는 일반적으로 분리 흡착을 촉진하면서 친수성을 향상시키는 것으로 발견된다.^[44]

참고 항목

참조

추가 읽기

• de Gennes, Pierre-Gilles; Brochard-Wyart, Françoise; Quéré, David (2004). Capillarity and Wetting Phenomena. Springer New York. doi:10.1007/978-0-387-21656-0. ISBN 978-1-4419-1833-8. S2CID 137894832.
• Victor M. Starov; Manuel G. Velarde; Clayton J. Radke (2 April 2007). Wetting and Spreading Dynamics. CRC Press. ISBN 978-1-4200-1617-8.

외부 링크

• 습윤성이란 무엇인가?
• Wikimedia Commons의 Wetting 관련 미디어