APL 구문 및 기호
APL syntax and symbols프로그래밍 언어 APL은 어휘가 아닌 기호로 특징지어진다: 그것의 원형은 단어가 아닌 기호로 나타난다.이 기호들은 [1]원래 알고리즘을 설명하기 위한 수학적 표기법으로서 고안되었다.APL 프로그래머는 함수 및 연산자(예를 들어 ×/의 제품)를 논의할 때 비공식 이름을 할당하는 경우가 많지만, 언어에 의해 제공되는 핵심 함수 및 연산자는 텍스트 이외의 기호로 표시됩니다.
단항 함수 및 쌍항 함수
대부분의 기호는 함수 또는 연산자를 나타냅니다.단항 함수는 오른쪽의 모든 것을 평가한 결과를 인수로 받아들입니다.(통상적인 방법으로 괄호로 처리됩니다.)이항 함수는 왼쪽에 첫 번째 데이터 항목인 또 다른 인수를 가집니다.많은 기호는 단항함수와 쌍항함수 모두를 나타내며 용도에 따라 해석됩니다.예를 들어, § 3.2는 인수 위에 있지 않은 최대 정수인 3을 나타내고, 3⁄2는 2개의 인수 중 작은 정수인 2를 나타냅니다.
함수 및 연산자
APL은 데이터(참조 관계 연산자 및 일반적으로 연산자)와 동일한 용어를 사용하는 다른 프로그래밍 언어와는 달리 함수의 진행자로서 헤비사이드의 의미에서의 연산자라는 용어를 사용한다.다른 프로그래밍 언어에서도 이 용어를 함수와 상호 호환되게 사용하는 경우가 있지만, 두 용어 모두 APL에서 [2][3][4][5][6]더 정확하게 사용됩니다.APL 기호의 초기 정의는 기호가 어떻게 [7]분류되는지에 대해 매우 구체적이었다.예를 들어 연산자 축소는 슬래시로 나타내며, 함수 피연산자를 개재시킴으로써 한 축에 따른 배열을 축소한다.reduce의 예:
×/2 3 4 24 | << APL > > > << 축소 연산자 / 왼쪽에서 사용 | 2×3×4 24 |
위의 경우 축소 또는 슬래시 연산자가 곱셈 함수를 조정합니다.식 ×/2 3 4는 배열을 곱하여 스칼라(1 요소만) 결과를 평가합니다.위의 경우는 단순화되어 있습니다.몇 개 이상의 숫자를 곱(더하기, 빼기 또는 나누기)하는 것을 상상해 보십시오.(벡터에서 ×/는 모든 원소의 곱을 반환합니다.)
1 0 1\45 67 45 0 67 | << APL의 반대 결과 >> << 왼쪽에서 사용되는 쌍방향 함수 확장 \ 오른쪽에서 사용되는 dynadic 함수 복제 > | 1 0 1/45 0 67 45 67 |
위의 쌍방향 함수 예[왼쪽 및 오른쪽 예제](같은 / 기호, 오른쪽 예제 사용)는 \ expand 및 / replicate 함수의 왼쪽 인수로 부울 값(0 및 1s)을 사용하여 완전히 반대되는 결과를 생성하는 방법을 보여줍니다.왼쪽에서는 부울 0이 발생하여 3 요소 벡터 {45 0 67}이 되는 2- 요소 벡터 {45 67}이(가) 확장됩니다. APL이 벡터에 0을 삽입한 방법에 주목하십시오.반대로 오른쪽에서는 정반대입니다.3 요소 벡터는 2 요소만 됩니다.부울 0s는 diadic / slash 함수를 사용하여 항목을 삭제합니다.APL 기호는 숫자 이외의 데이터 유형을 사용하여 항목의 목록(벡터)에서도 작동합니다. 예를 들어 위의 숫자 벡터 {4567} 대신 문자열 {"Apples" "Orange"}의 2-element 벡터를 대체할 수 있습니다.
구문 규칙
APL에는 함수 또는 연산자의 우선순위 계층이 없습니다.APL은 다른 프로그래밍 언어의 일반적인 연산자 우선 순위를 따르지 않습니다.예를 들어 다음과 같습니다.×피연산자를 바인드하지 않는 것은 다음과 같습니다.+연산자 우선 순위 대신 APL은 범위의 개념을 정의합니다.
함수의 범위에 따라 인수가 결정됩니다.함수는 오른쪽 범위가 길다. 즉, 모든 것을 오른쪽의 올바른 인수로 받아들인다.쌍방향 함수는 왼쪽 범위가 짧습니다. 왼쪽 인수로 왼쪽의 첫 번째 데이터 조각을 사용합니다.예를 들어, (아래 맨 왼쪽 열은 APL 사용자 세션의 실제 프로그램 코드, 들여쓰기 = 실제 사용자 입력, 들여쓰기되지 않음 = APL 인터프리터에 의해 반환된 결과입니다.)
1 ÷ 2 ⌊ 3 × 4 - 5 ¯0.3333333333 1 ÷ 2 ⌊ 3 × ¯1 ¯0.3333333333 1 ÷ 2 ⌊ ¯3 ¯0.3333333333 1 ÷ ¯3 ¯0.3333333333 | << 첫 번째 노트에는 괄호가 없습니다. 2단계) 3 곱하기 -1 = -3. |
연산자는 함수 또는 데이터 피연산자를 가질 수 있으며, 쌍방향 또는 단방향 함수로 평가할 수 있다.연산자는 왼쪽 범위가 길다.연산자는 왼쪽 연산자로 가장 긴 함수를 왼쪽으로 가져갑니다.예를 들어 다음과 같습니다.
∘.=/⍳¨3 3 1 0 0 0 1 0 0 0 1 | APL 원자 또는 단편 하위 분석(전체 설명): diaeresis θ 또는 mini double-dot은 각각 반복 또는 반복을 의미하며, 각각 개별적으로 iota를 수행하여 iota를 반복한다(인간의 역어로 APL 인터프리터는 각 사용 iota에 대해 3을 읽는다). 간결하게: 각 3에 대해 iota를 읽는다. |
각 측정 시스템의 왼쪽 피연산자¨index function함수입니다.파생 함수 ⍳¨모나디컬하게 사용되며 오른쪽 연산자와 벡터3 3. 각 스코프의 왼쪽은 reduced 연산자에 의해 종료되며 슬래시로 나타납니다.왼쪽 피연산자는 왼쪽의 함수식, 즉 등가함수의 바깥쪽 곱입니다.∘.=/의 결과는 단항 함수입니다.함수의 통상적인 긴 오른쪽 범위에서는 §3의 결과를 올바른 인수로 받아들인다.따라서
(가) (가) (가) 1 2 3 1 2 3 3 (가) 3 (가) 3 .=param3 1 0 0 0 0 0 0 1 ⍳3 3 1 2 3 0 . = / param3 3 1 0 0 0 0 0 1 |
비슷하게 생성된 1과 0의 행렬은 다음과 같이 생성됩니다. |
임 ← ∘.=⍨∘⍳ 임 3 1 0 0 0 1 0 0 0 1 | 일부 APL 인터프리터는 합성 연산자 and 및 통근 연산자 ⍨를 지원합니다.예를 들어 foo bar는 정의된 함수 bar의 결과에 정의된 함수 foo를 적용하는 가상의 함수일 수 있도록 앞의 함수 foo는 함께 기능을 수행하며 foo와 boo와 bar는 기존의 함수를 나타낼 수 있습니다.diadic 함수가 통근에 의해 모델레이트 되어 모나디컬하게 사용되는 경우 오른쪽 인수도 왼쪽 인수로 간주됩니다.따라서, 파생 또는 합성 함수(왼쪽의 im)는 오른쪽 인수, 매개 변수 또는 피연산자 = 3을 사용하여 9자리 식별 행렬을 반환하기 위해 APL 사용자 세션에서 사용됩니다. |
편지들←"ABCDE" 편지들 ABCDE ⍴편지들 5 검색←"CABS" 검색 캡 ⍴검색 4 편지들 ⍳ 검색 3 1 2 6 | APL을 사용하여 문자 벡터의 요소를 인덱스 또는 검색(또는 검색하지 않음)하는 예: 첫째, 변수 Letters에는 5개 요소의 벡터(이 경우 알파벳 문자)가 할당됩니다. 문자의 모양 or 또는 문자 벡터 길이는 5입니다. 변수 찾기: 문자에서 검색할 항목이 할당되어 있으며 길이는 4자입니다. 1 2 3 4 5 << 벡터 위치 또는 색인 번호(문자) 왼쪽에서 diadic 함수 iota는 왼쪽 인수(Letters)에서 검색 문자열(iota의 오른쪽 인수 FindIt)을 검색합니다. Iota는 Letters의 위치 3에서 문자 "C"를 찾고 위치 1에서 "A"를, 위치 2에서 "B"를 찾습니다.Iota는 문자 "S"를 찾을 수 없습니다. 문자 길이보다 1 더 큰 숫자 6을 반환합니다.Iota는 문자를 찾았습니다. 'CAB' (3.12)Iota는 "S"(6)를 올바르게 찾지 못했습니다. |
모나드 함수
| 이름 | 표기법 | 의미. | 유니코드 코드 포인트 |
|---|---|---|---|
| 굴리다 | ?B | 첫 번째 B 정수에서 무작위로 선택된 정수 | U+003F ? |
| 천장. | ⌈B | B 이상의 최소 정수 | U+2308 ⌈ |
| 바닥. | ⌊B | B보다 작거나 같은 최대 정수 | U+230A ⌊ |
| 모양, 노 | ⍴B | B의 각 차원에 있는 성분 수 | U+2374 ⍴ |
| 안 돼, 틸드 | ∼B | 논리: ~1은 0, ~0은 1 | U+223C ∼ |
| 절대값 | ∣B | 매그니튜드 B | U+2223 ∣ |
| 인덱스 생성기(Iota) | ⍳B | 첫 번째 B 정수의 벡터 | U+2373 ⍳ |
| 지수 | ⋆B | e의 B승 | U+22C6 ⋆ |
| 부정 | −B | B의 변경 부호 | U+2212 − |
| 켤레 | +B | B의 복소 켤레(실수는 변경되지 않고 반환됨) | U+002B + |
| 시그넘 | ×B | B의 경우 1<0, B=0, B>0의 경우 1 | U+00D7 × |
| 호혜적 | ÷B | 1 나누기 B | U+00F7 ÷ |
| 라벨, 카테나테, 라미네이트 | ,B | B를 벡터로 재형성합니다. | U+002C , |
| 행렬 역행렬, Monadic Quad Divide | ⌹B | 행렬 B의 역수 | U+2339 ⌹ |
| 파이배 | ○B | π를 곱하다 | U+25CB ○ |
| 로그 | ⍟B | B의 자연 로그 | U+235F ⍟ |
| 반전 | ⌽B | 마지막 축을 따라 B의 역요소 | U+233D ⌽ |
| 반전 | ⊖B | 첫 번째 축을 따라 B의 역요소 | U+2296 ⊖ |
| 등급업 | ⍋B | B를 오름차순으로 배열하는 B의 지수 | U+234B ⍋ |
| 하향 조정 | ⍒B | B를 내림차순으로 배열하는 B의 지수 | U+2352 ⍒ |
| 실행 | ⍎B | APL 식 실행 | U+234E ⍎ |
| 모나드 형식 | ⍕B | B의 문자 표현 | U+2355 ⍕ |
| 모나치 전치 | ⍉B | B의 축을 반대로 하다 | U+2349 ⍉ |
| 요인 | !B | 정수 1에서 B까지의 곱 | U+0021 ! |
다이아딕 함수
| 이름 | 표기법 | 의미. | 유니코드 코드 포인트 |
|---|---|---|---|
| 더하다 | A+B | A와 B의 합계 | U+002B + |
| 빼다 | A−B | A 마이너스 B | U+2212 − |
| 곱셈 | A×B | A에 B를 곱한 것 | U+00D7 × |
| 나누다 | A÷B | A를 B로 나누다 | U+00F7 ÷ |
| 지수화 | A⋆B | A는 B의 거듭제곱이 된다. | U+22C6 ⋆ |
| 원형 | A○B | A가 선택한 B의 삼각 함수 A=1: sin(B) A=5: sinh(B) A=2: cos(B) A=6: cosh(B) A=3: tan(B) A=7: tanh(B) 음수는 각 함수의 역수를 생성합니다. | U+25CB ○ |
| 우리 모두 동의한거다. | A?B | 첫 번째 B 정수에서 랜덤으로 선택된 고유 정수 | U+003F ? |
| 멤버십(입실론) | A∈B | B에 존재하는 A의 요소의 경우 1, 존재하지 않는 경우 0. | U+2208 ∈ |
| 찾아라, 엡실론 언더바 | A⍷B | B에 있는 복수 항목 배열 A의 시작점을 나타내는 1. 그렇지 않은 경우 0. | U+2377 ⍷ |
| 최대, 상한 | A⌈B | A 또는 B의 큰 값 | U+2308 ⌈ |
| 최소, 바닥 | A⌊B | A 또는 B의 작은 값 | U+230A ⌊ |
| 리셰이프, 다이아딕 로 | A⍴B | 데이터 B가 있는 형상 A의 배열 | U+2374 ⍴ |
| 가지고 가다 | A↑B | ×A에 따라 B의 첫 번째(또는 마지막) A 요소를 선택합니다. | U+2191 ↑ |
| 떨어지다 | A↓B | ×A에 따라 B의 첫 번째(또는 마지막) A 요소를 제거합니다. | U+2193 ↓ |
| 디코드 | A⊥B | A에서 계수가 B인 다항식의 값 | U+22A5 ⊥ |
| 부호화 | A⊤B | B의 값의 Base-A 표현 | U+22A4 ⊤ |
| 잔류물 | A∣B | B 모듈로 A | U+2223 ∣ |
| 카테네이션 | A,B | A의 요소에 부가되는 B의 요소 | U+002C , |
| 확장, Dyadic 백슬래시 | A\B | A의 0에 해당하는 0(또는 공백)을 B에 삽입합니다. | U+005C \ |
| 압축, Dynadic 슬래시 | A/B | A의 요소에 해당하는 B의 요소를 선택합니다. | U+002F / |
| 색인, Dyadic Iota | A⍳B | A에서 B의 위치(색인)1+⍴A발견되지 않으면 | U+2373 ⍳ |
| 행렬 분할, 2차 사분할 | A⌹B | 선형 방정식 시스템에 대한 해, 다중 회귀 Ax = B | U+2339 ⌹ |
| 회전 | A⌽B | B의 요소는 회전 A 위치입니다. | U+233D ⌽ |
| 회전 | A⊖B | B의 요소는 첫 번째 축을 따라 A 위치를 회전합니다. | U+2296 ⊖ |
| 로그 | A⍟B | 밑수 A에 대한 B의 로그 | U+235F ⍟ |
| 다이애딕 형식 | A⍕B | A에 따라 B를 문자 행렬로 포맷합니다. | U+2355 ⍕ |
| 일반 전치 | A⍉B | B의 축은 A에 의해 정렬됩니다. | U+2349 ⍉ |
| 조합 | A!B | 한 번에 A를 취한 B의 조합 수 | U+0021 ! |
| 디아레시스, 디에레시스, 더블닷 | A¨B | 각각에 걸쳐 수행하거나 개별적으로 수행하거나, B = 이 경우, A = 수행 또는 사용하기 위한 작업(예: iota) | U+00A8 ¨ |
| 보다 적은 | A<B | 비교: 참일 경우 1, 거짓일 경우 | U+003C < > |
| 이하 | A≤B | 비교: 참일 경우 1, 거짓일 경우 | U+2264 ≤ |
| 동등. | A=B | 비교: 참일 경우 1, 거짓일 경우 | U+003D = |
| 이상 | A≥B | 비교: 참일 경우 1, 거짓일 경우 | U+2265 ≥ |
| 보다 크다 | A>B | 비교: 참일 경우 1, 거짓일 경우 | U+003E > |
| 동일하지 않다 | A≠B | 비교: 참일 경우 1, 거짓일 경우 | U+2260 ≠ |
| 또는 | A∨B | 부울 논리: A와 B가 모두 0이면 0(False), 그렇지 않으면 1입니다.Alt: A 또는 B = 1인 경우 1(참) | U+2228 ∨ |
| 그리고. | A∧B | 부울 로직: A와 B가 모두 1, 그렇지 않으면 0(False)이면 1(True) | U+2227 ∧ |
| 도 아니다 | A⍱B | Boolean Logic: A와 B가 모두 0이면 1, 그렇지 않으면 0입니다.Alt: ~syslog = 없음 또는 | U+2371 ⍱ |
| 낸드 | A⍲B | 부울 로직: A와 B가 모두 1이면 0, 그렇지 않으면 1입니다.Alt: ~syslog = 없음 | U+2372 ⍲ |
| 왼쪽 | A⊣B | A | U+22A3 ⊣ |
| 맞다 | A⊢B | B | U+22A2 ⊢ |
연산자 및 축 표시기
| 이름 | 기호. | 예 | 의미(예) | 유니코드 코드 포인트 시퀀스 |
|---|---|---|---|---|
| 축소(마지막 축), 슬래시 | / | +/B | B의 합계 | U+002F / |
| 축소(첫 번째 축) | ⌿ | +⌿B | 요약 B | U+233F ⌿ |
| 스캔(마지막 축), 백슬래시 | \ | +\B | B에 걸친 실행 합계 | U+005C \ |
| 스캔(첫 번째 축) | ⍀ | +⍀B | 총계 B | U+2340 ⍀ |
| 내부 제품 | . | A+.×B | A와 B의 행렬 곱 | U+002E . |
| 외부 제품 | ∘. | A∘.×B | A와 B의 외부 제품 | U+2218, U+002E. |
참고: 축소 및 스캔 연산자는 왼쪽에 쌍방향 함수를 예상하여 오른쪽에 있는 벡터에 적용되는 단방향 복합 함수를 형성합니다.
곱셈 연산자 "."는 왼쪽과 오른쪽의 벡터에 적용되는 2차 합성 함수를 왼쪽과 오른쪽 모두에 기대합니다.점 왼쪽의 함수가 """(null을 나타냄)이면 복합 함수는 외부 산물이고 그렇지 않으면 내부 산물입니다.기존 행렬 곱셈을 위한 내부 곱셈은 + 및 × 함수를 사용하여 이들을 다른 2진함수로 대체하면 유용한 대체 연산을 얻을 수 있습니다.
일부 함수는 (사각형) 괄호 안에 축 표시기가 있을 수 있습니다. 즉, 함수와 배열 사이에 표시되므로 배열 뒤에 쓴 배열 첨자와 혼동해서는 안 됩니다.예를 들어, θ(역방향) 함수와 2차원 배열이 주어진 경우 기본적으로 함수는 마지막 축을 따라 작동하지만 축 표시기를 사용하여 변경할 수 있습니다.
A←4 3⍴⍳12 A 1 2 3 4 5 6 7 8 9 10 11 12 ⌽A 3 2 1 6 5 4 9 8 7 12 11 10 ⌽[1]A 10 11 12 7 8 9 4 5 6 1 2 3 ⊖⌽A 12 11 10 9 8 7 6 5 4 3 2 1 ⍉A 1 4 7 10 2 5 8 11 3 6 9 12 |
이제 A는 기호 θ가 시각적으로 나타내듯이 수직 축을 따라 반사되거나 뒤집힙니다. 이제 A는 [1] 축 표시기 또는 첫 번째 치수 수식자를 사용하여 반사됩니다.그 결과 변수 A가 수직이 아닌 수평 축에 반사되었습니다. 이제 A는 수직 θ와 수평 θ 모두 반사됩니다. A는 기호 θ가 시각적으로 나타내듯이 행-콜이 교환되도록 3행×4col 매트릭스로 치환된다.여기서의 결과를 A에 저장되어 있는 최상위 행렬과 비교합니다.이러한 유형의 데이터 변환은 시계열 분석 및 공간 좌표(예: 두 개)에 유용합니다. |
특정한 경우로, 2진수 카테네이트 ", 함수 뒤에 축 표시기(또는 기호/함수의 축 수정자)가 이어지는 경우, 축 표시기가 지수[8] 원점보다 작거나 큰지 여부에 따라 두 개의 어레이를 적층(하부 그림에서는 지수 원점 = 1)하는 데 사용할 수 있습니다.
B←1 2 3 4 C←5 6 7 8 B,C 1 2 3 4 5 6 7 8 B,[0.5]C 1 2 3 4 5 6 7 8 B,[1.5]C 1 5 2 6 3 7 4 8 | 왼쪽에서 변수 'B'는 먼저 연속된 4개의 정수(예를 들어 θ4)의 벡터가 할당된다. |
네스트된 어레이
배열은 요소가 벡터 또는 표 형태로 선형으로 그룹화된 구조이며, 더 높은 차원(3D 또는 입방체, 4D 또는 시간에 따른 입방체 등)을 가집니다.문자와 숫자를 모두 포함하는 배열을 혼합 [9]배열이라고 합니다.요소를 포함하는 배열 구조를 중첩 [10]배열이라고 합니다.
| APL 인터프리터를 사용한 사용자 세션 | 설명. |
|---|---|
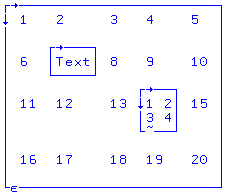
X←4 5⍴⍳20 X 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 X[2;2] 7 § IO 1 X[1;1] 1 |
2행 - 2열의 요소 X[2;2]는 현재 정수 = 7입니다. 초기 인덱스 원본 "IO 값 = 1. 따라서 행렬 X 또는 X[1;1]의 첫 번째 원소는 1입니다. |
X[2;2]←⊂"텍스트" X[3;4]←⊂(2 2⍴⍳4) X 1 2 3 4 5 6 본문 8 9 10 11 12 13 1 2 15 3 4 16 17 18 19 20 | X [ row 2 ; col 2 ]의 요소를 둘러싸는 function 함수를 사용하여 (7에서) 중첩 벡터 "Text"로 변경합니다. X [ row 3 ; col 4 ]의 요소(이전에는 정수 14)는 4개의 연속된 정수로 이루어진 최소 밀폐형 또는 δ 내포형 2x2 행렬이 됩니다. X에는 숫자, 텍스트 및 중첩된 요소가 포함되어 있으므로 혼합 배열과 중첩된 배열이 모두 됩니다. |
흐름 제어
사용자는 변수와 마찬가지로 텍스트 이외의 기호가 아닌 이름으로 식별되는 커스텀 함수를 정의할 수 있다.함수 헤더는 사용자 지정 함수가 niladic(인수 없음), monadic(오른쪽 인수 하나) 또는 dynadic(왼쪽 및 오른쪽 인수)인지 여부, 결과의 로컬 이름(← 할당 화살표 왼쪽에 있음), 로컬 변수(각각각 세미콜론 ';'로 구분됨)를 정의합니다.
| Niladic 함수 PI 또는 δ(pi) | 모노딕 함수 서클 영역 | Dynadic 함수 SEGENTAREA, 로컬 변수 포함 |
|---|---|---|
∇ 결과←PI 결과←○1 ∇ | ∇ 지역←서클 영역 RADIUS 지역←PI×RADIUS⋆2 ∇ | ∇ 지역←도 세그먼트 영역 RADIUS ; 프랙션 ; CA 프랙션←도÷360 CA←서클 영역 RADIUS 지역←프랙션×CA ∇ |
식별자가 동일하지만 고유성이 다른 함수가 구별되는지 여부는 구현에서 정의됩니다.허용된 경우, 위의 모노딕 서클 영역과 다이애딕 세그먼트 영역을 모두 대체하기 위해 함수 CURVEAREA를 두 번 정의할 수 있으며, 모노딕 또는 다이애딕 함수는 참조된 컨텍스트에 의해 선택됩니다.
커스텀 다이애딕 함수는 보통 내장 함수와 같은 규약을 가진 파라미터에 적용할 수 있습니다.즉, 배열은 같은 수의 요소를 가지거나 그 중 하나에 확장되는 단일 요소를 가져야 합니다.여기에는 예외가 있다. 예를 들어 10진수 이전의 영국 통화를 달러로 변환하는 함수는 파운드, 실링 및 [11]펜스를 나타내는 정확히 세 가지 요소를 가진 매개변수를 취할 것으로 예상된다.
프로그램 또는 커스텀 함수 내에서 제어는 회선 번호 또는 명시적 라벨로 식별되는 문장으로 조건부로 전송될 수 있습니다.타깃이 0이면 프로그램이 종료되거나 함수의 호출자에게 반환됩니다.가장 일반적인 형식에서는 템플릿(조건)/타깃과 같이 APL 압축 함수를 사용합니다.템플릿(조건)/타깃은 조건을 0(false) 또는 1(true)로 평가한 후 이를 사용하여 타깃을 마스크합니다(조건이 false일 경우 무시되며 true일 경우 그대로 유지되므로 제어가 전송됩니다).
따라서 SegmentAREA 함수는 중단(바로 아래)하도록 수정되어 파라미터(DEORIES 및 RADIUS)가 다른 부호일 경우 0을 반환할 수 있습니다.
∇ 지역←도 세그먼트 영역 RADIUS ; 프랙션 ; CA ; 서명하다 세미콜론으로 표시되는 로컬 변수) 프랙션←도÷360 CA←서클 영역 RADIUS § 이 APL 코드문은 위에서 정의한 사용자 함수 서클 에리어를 호출합니다. 서명하다←(×도)≠×RADIUS § < APL 로직 TEST/판단: DEGRES와 RADIUS가 같은 SIGN 1-yes different(),), 0-no(동일 부호)를 가지고 있는지(사용되고 있음) 지역←0 § AREA set의 디폴트값 =0 →서명하다/0 branch 분기(여기서, 종료)는 SIGN=1인 반면 SIGN=0은 0으로 분기하지 않을 때 발생합니다. 0으로 분기하면 기능이 종료됩니다. 지역←프랙션×CA ∇ 위의 SEVENTAREA 함수는 파라미터가 스칼라 또는 단일 요소 배열인 경우 예상대로 동작하지만, 조건이 SIGN 배열의 단일 요소에 기반하기 때문에 다중 요소 배열인 경우 그렇지 않습니다. 한편, 사용자 함수는 벡터화된 인수를 올바르게 처리하도록 수정될 수 있습니다.APL은 벡터 처리 기능을 가진 컴퓨터가 어레이 동작을 병렬화하고 가능한 한 순서를 변경할 수 있도록 정의하기 때문에 동작이 예측 불가능한 경우가 있습니다.따라서 특히 벡터 또는 매트릭스 인수와 함께 사용할 경우 사용자 함수를 테스트 및 디버깅합니다.이는 커스텀 함수를 어레이에 명시적으로 적용할 뿐만 아니라 결과 테이블 생성 등 쌍방향 함수를 합리적으로 사용할 수 있는 모든 장소에서의 사용에 영향을 미칩니다.
90 180 270 ¯90 ∘.세그먼트 영역 1 ¯2 4 0 0 0 0 0 0 0 0 0 0 0 0 보다 간결하고 때로는 더 나은 방법 - 함수를 공식화하는 것은 제어의 명시적 이전을 피하는 대신 모든 또는 예상 조건에서 올바르게 평가하는 표현을 사용하는 것이다.한 쪽 또는 두 쪽 입력 인수가 올바르지 않을 때 함수를 실패시키는 것이 올바른 경우가 있습니다.사용자에게 정확히는 사용된 한 쪽 또는 두 쪽 인수가 모두 잘못되었음을 알리기 위해서입니다.다음은 위의 SEGENTAREA 함수보다 더 간결합니다.다음으로 벡터화된 인수를 올바르게 처리합니다.
∇ 지역←도 세그먼트 영역 RADIUS ; 프랙션 ; CA ; 서명하다 프랙션←도÷360 CA←서클 영역 RADIUS 서명하다←(×도)≠×RADIUS 지역←프랙션×CA×~서명하다 § 이 APL 문장은 원라이너로서 더 복잡하지만 벡터화된 주장을 해결한다: 트레이드오프 복잡성 대 트레이드오프 ∇ 90 180 270 ¯90 ∘.세그먼트 영역 1 ¯2 4 0.785398163 0 12.5663706 1.57079633 0 25.1327412 2.35619449 0 37.6991118 0 ¯3.14159265 0 브런치라고도 불리는 명시적인 관리 이전을 회피하는 것은 검토 또는 세심하게 관리하지 않으면 지나치게 복잡한 1개의 라이너, 즉 "잘못 이해되고 복잡한 관용어" 및 "쓰기 전용" 스타일의 사용을 촉진할 수 있으며, 이는 Edsger Dijkstra와 [12]같은 영향력 있는 해설자들에게 APL을 귀하게 만드는 데 거의 도움이 되지 않습니다.그러나 반대로 APL 숙어는 재미있고 교육적이며 유용한 코멘트 »와 함께 사용될 수 있습니다. 예를 들어 숙어의 출처와 의도된 의미 및 기능을 포함합니다.여기 APL 관용구 리스트, IBM APL2 관용구 리스트[13], 핀란드어 APL 관용구 라이브러리가 있습니다.
여러가지 종류의
| 이름 | 기호. | 예 | 의미(예) | 유니코드 코드 포인트 |
|---|---|---|---|---|
| 하이[14] 마이너스 | ¯ | ¯3 | 음수를 나타냅니다. | U+00AF ¯ |
| 램프, 코멘트 | ⍝ | ⍝This is a comment | ①의 오른쪽에 있는 것은 모두 코멘트를 나타냅니다. | U+235D ⍝ |
| 오른쪽 화살표, 지점, 이동 | → | →This_Label | →This_Label은 APL 실행을 This_Label로 전송합니다. | U+2192 → |
| 할당, 왼쪽 화살표, 다음으로 설정 | ← | B←A | B←A는 A와 일치하도록 B의 값과 모양을 설정합니다. | U+2190 ← |
대부분의 APL 실장에서는 다수의 시스템 변수와 함수가 지원되고 있습니다.보통 앞에는 "("") 및/또는 "("hook=close 괄호") 문자가 붙습니다.쿼드 문자는 Unicode 결측 문자 기호와 동일하지 않습니다.원본 IBM APL은 어레이를 1개의 새로운 변종 기반으로 하지만 0을 기반으로 하기 때문에 특히 중요하고 광범위하게 구현된 변수입니다.
| APL 인터프리터를 사용한 사용자 세션 | 묘사 |
|---|---|
X←⍳12 X 1 2 3 4 5 6 7 8 9 10 11 12 § IO 1 X[1] 1 | X는 =를 12개의 연속 정수의 벡터로 설정합니다. 초기 인덱스 원본 "IO 값 = 1.따라서 벡터 X 또는 X[1] = iota 값 {1 2 3 4 5 ...}의 벡터당 1의 첫 번째 위치가 됩니다. |
§ IO←0 X[1] 2 X[0] 1 | Index Origin ioIO가 0으로 변경되었습니다.따라서 벡터 X의 '첫 번째 지수 위치'는 1에서 0으로 바뀝니다.그 결과 X[1]는 {1 2 3 4 5 ...에서2를 참조하거나 가리킵니다.} 및 X[0]는 1을 참조합니다. |
§ WA 41226371072 | Quad WA 또는 다른 동적 시스템 변수인 waWA는 APL 워크스페이스 및 프로그램에서 사용할 수 있는 미사용 총 여유 작업영역의 41,226메가바이트 또는 약 41기가바이트를 나타냅니다.이 수치가 낮아지거나 0에 가까워지면 가상 메모리를 늘리기 위해 컴퓨터에 RAM(랜덤 액세스 메모리), 하드 디스크(HDD) 용량 또는 이 둘의 조합이 더 필요할 수 있습니다. |
)바 X | APL에서 [15]시스템 기능을 VARS, VARS는 현재 워크스페이스에 존재하는 사용자 변수 이름을 표시합니다. |
사용자가 현재 작업 공간을 저장하거나 APL 환경을 종료하기 위해 사용할 수 있는 시스템 기능도 있습니다(예: ). OFF(오른쪽 괄호 또는 [16]후크를 사용하여 후크 명령 또는 함수라고도 함).이러한 쿼드 및 후크 기능의 표준화가 있습니다.
폰트
Unicode 기본 다국어 영역은 기타 기술 [17]블록에 APL 기호를 포함하므로, 일반적으로 대부분의 최신 운영 체제에 설치된 더 큰 Unicode 글꼴에서 정확하게 렌더링됩니다.이러한 글꼴은 APL 글리프에 익숙한 타이포그래퍼에 의해 디자인되는 경우는 거의 없습니다.따라서 정확하지만 APL 프로그래머에게는 글리프가 낯설거나 서로 구별하기 어려울 수 있습니다.
일부 Unicode 글꼴(APLX Uplate, APL385 Unicode 및 SimPL)은 APL을 잘 표시하도록 설계되었습니다.
Unicode 이전 APL 인터프리터는 APL 문자를 ASCII 문자 집합에서 자주 사용되지 않는 위치(일반적으로 상위 128 코드 포인트)에 매핑하는 글꼴이 제공되었습니다.이러한 매핑(및 국가별 변형)은 각 APL 벤더의 인터프리터에게 고유할 수 있으며, 이로 인해 웹상의 APL 프로그램을 텍스트 파일 및 매뉴얼로 표시하는 데 많은 문제가 발생하였습니다.
APL2 키보드 기능과 기호 매핑
APL On/Off 키(맨 오른쪽 상단 키)를 확인합니다.또한 키보드는 약 55개의 고유 키(위의 테이블당 68개의 비교 기호를 포함하지만 모노딕 및 다이애딕 테이블에 여러 개의 기호가 표시됨)를 가지고 있습니다. APL 기호 키(55 APL 함수(연산자)는 IBM의 5110 APL 참조 설명서에 나열되어 있으므로 이론적으로 alt, shift 및 ctrl 키를 사용하여 최대값을 허용했을 것입니다.약 59(키) *4(2키 누르기) *3(2키 누르기) 또는 472개의 다른 최대 키 조합으로, 512개의 EBCDIC 문자 최대값(256자 x 2 코드)에 근접합니다.다시, 이론적으로, 여기에 표시된 키보드는 약 472개의 다른 APL 기호/기능을 키보드 입력으로 능동적으로 사용할 수 있게 합니다.실제로 초기 버전은 약 55개의 APL 특수 기호(문자, 숫자, 구두점 등 제외)에 해당하는 것만 사용했습니다.따라서 초기 APL은 숫자, 문자, 구두점 등을 제외한 키보드 번호 키 제한에 기반하여 당시 기호 언어의 사용 가능성의 약 11%(55/472)만을 사용하고 있었다.EBCDIC는 256개의 개별 문자만 허용하고 ASCII는 128개의 문자만 허용했기 때문에 키보드 기호 사용률은 100%에 가깝고 매우 효율적이었다.
퍼즐을 풀다
APL은 수학 퍼즐을 푸는 데 매우 유용한 것으로 입증되었으며, 그 중 몇 가지는 아래에 설명되어 있습니다.
파스칼 삼각형
파스칼의 삼각형을 예로 들어보자.이 삼각형 배열은 행의 끝에 있는 숫자가 1이고 다른 숫자는 각각 그 바로 위에 있는 행에서 가장 가까운 두 숫자의 합이다(꼭지점, 1이 맨 위에 있음).다음은 Pascal의 삼각형을 시각적으로 묘사하는 APL 원라이너 기능입니다.
파스칼←{0~¨⍨a⌽⊃⌽∊¨0,¨¨a∘!¨a←⌽⍳⍵} ① Pascal이라는 한 줄 사용자 기능 만들기 파스칼 7 § 함수 Pascal을 7줄 동안 실행하여 아래 결과를 보여줍니다. 1 1 2 1 3 3 1 4 6 4 1 5 10 10 5 1 6 15 20 15 6 1 7 21 35 35 21 7 소수, 인자에 의한 반증명
소수(소수번호는 1보다 큰 자연수이며, 1 이외의 양의 제수가 없는 자연수)를 N까지 결정합니다.Ken Iverson은 이 문제에 대한 다음 원라이너 APL 솔루션을 개발한 것으로 알려져 있습니다.
§ CR 'Prime Numbers' § APL 사용자 기능 Prime Numbers 표시 소수점←프라임넘버스 N § 함수는 오른쪽 arg N을 1개 취합니다(예를 들어 1의 소수 표시).내부 N) 소수점←(2=+⌿0=(⍳N)∘.⍳N)/⍳N § 켄 아이버슨 원라이너 프라임넘버스 100 ② 1 ~ 100의 모든 소수 표시 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 ⍴프라임넘버스 100 25 ①100까지의 소수는 25개입니다. 수학적 해법의 역수 또는 역수를 조사하는 것이 자주 필요합니다(숫자의 정수 요인).분해 인자를 나열하여 1부터 15까지의 정수 부분 집합에 대해 비소수임을 증명합니다.1이 아닌 요인(#은 1로 나누어짐)은 무엇입니까?
§ CR 'Prove Non Prime' Z←Provate Non Prime(비프라임 증명) R ②정수 R의 모든 인자를 표시 - 1과 숫자 자체를 제외하고, § 즉, Non-Prime을 증명한다.문자열 'prime'는 소수 정수로 반환됩니다. Z←(0=(⍳R) R)/⍳R ∙ 정수 R의 모든 요인을 파악하여 Z에 저장 Z←(~(Z∊1,R))/Z ② Z에서 1과 숫자를 인수로 삭제한다. →(0=⍴Z)/Provate Non Prime Is Prime ∙ 0 형상이면 다른 인자가 없으므로 프라임 Z←R,(⊂"요인 (1 제외)"),(⊂Z),§ TCNL ② 숫자 R과 그 인자(1, itself 제외), 새 줄 문자 표시 →0 ② 비프라임일 경우 기능 완료 Provate Non Prime Is Prime: Z←R,(⊂'프라임'),§ TCNL § 숫자가 소수일 경우 함수는 여기에 분기합니다. Provate Non Prime(비프라임 증명) ¨⍳15 ① 1~15(iota 15)의 정수())마다 비소수를 증명한다. 1 프라임 2 프라임 3 프라임 4 요인들(제외하고 1) 2 5 프라임 6 요인들(제외하고 1) 2 3 7 프라임 8 요인들(제외하고 1) 2 4 9 요인들(제외하고 1) 3 10 요인들(제외하고 1) 2 5 11 프라임 12 요인들(제외하고 1) 2 3 4 6 13 프라임 14 요인들(제외하고 1) 2 7 15 요인들(제외하고 1) 3 5 피보나치 수열
Fibonacci 번호 시퀀스를 생성합니다.여기서 시퀀스 내의 각 후속 번호는 앞의 2개의 합계입니다.
§ CR '피보나치 ② 표시기능 피보나치 피보나치넘←피보나치 N번째;입출력 ④ Funct 헤더, funct name=Puniconacci, 1 우측 arg Nth의 monadic funct, local var IOwas 및 반환된 num. ② 피보나치 시퀀스 번호를 생성합니다.여기서 Nth는 시퀀스 내의 피보나치 번호의 위치 번호입니다.<< 함수 설명 입출력←§ IO ⋄ § IO←0 ⋄ 피보나치넘←↑0 1↓↑+.×/N번째/⊂2 2⍴1 1 1 0 ⋄ § IO←입출력 ② 이 기능이 올바르게 작동하려면 ②IO를 0으로 설정해야 합니다. 피보나치¨⍳14 § 이 APL 스테이트먼트는 다음과 같습니다.정수 1의 각(') 정수 번호(iota 또는 ')에 걸쳐 피보나치 시퀀스를 생성합니다.14. 0 1 1 2 3 5 8 13 21 34 55 89 144 233 § 생성된 시퀀스, 즉 APL의 인터프리터에 의해 생성된 피보나치 시퀀스. 추가 정보
- Polivka, Raymond P.; Pakin, Sandra (1975). APL: The Language and Its Usage. Prentice-Hall. ISBN 978-0-13-038885-8.
- Reiter, Clifford A.; Jones, William R. (1990). APL with a Mathematical Accent (1 ed.). Taylor & Francis. ISBN 978-0534128647.
- Thompson, Norman D.; Polivka, Raymond P. (2013). APL2 in Depth (Springer Series in Statistics) (Paperback) (Reprint of the original 1st ed.). Springer. ISBN 978-0387942131.
- Gilman, Leonard; Rose, Allen J. (1976). A. P. L.: An Interactive Approach (Paperback) (3rd ed.). ISBN 978-0471093046.
「 」를 참조해 주세요.
- 기타 기술 – APL 키를 포함한 Unicode 블록
- APL (코드 페이지) keyboard 키보드 레이아웃– 보다 현대적인 APL 키보드 레이아웃 정보
레퍼런스
- ^ Iverson, Kenneth E. (1962-01-01). "A Programming Language". Proceedings of the May 1–3, 1962, Spring Joint Computer Conference. AIEE-IRE '62 (Spring). New York, NY, USA: ACM: 345–351. doi:10.1145/1460833.1460872.
- ^ Baronet, Dan. "Sharp APL Operators". archive.vector.org.uk. Vector - Journal of the British APL Association. Retrieved 13 January 2015.
- ^ MicroAPL. "Primitive Operators". www.microapl.co.uk. MicroAPL. Retrieved 13 January 2015.
- ^ MicroAPL. "Operators". www.microapl.co.uk. MicroAPL. Retrieved 13 January 2015.
- ^ Progopedia. "APL". progopedia.com. Progopedia. Retrieved 13 January 2015.
- ^ Dyalog. "D-functions and operators loosely grouped into categories". dfns.dyalog.com. Dyalog. Retrieved 13 January 2015.
- ^ IBM. "IBM 5100 APL Reference Manual" (PDF). bitsavers.trailing-edge.com. IBM. Archived from the original (PDF) on 14 January 2015. Retrieved 14 January 2015.
- ^ Brown, Jim (1978). "In defense of index origin 0". ACM SIGAPL APL Quote Quad. 9 (2): 7. doi:10.1145/586050.586053.
- ^ MicroAPL. "APLX Language Manual" (PDF). www.microapl.co.uk. MicroAPL - Version 5 .0 June 2009. p. 22. Retrieved 31 January 2015.
- ^ Benkard, J. Philip (1992). "Nested Arrays and Operators: Some Issues in Depth". ACM SIGAPL APL Quote Quad. 23 (1): 7–21. doi:10.1145/144045.144065. ISBN 978-0897914772.
- ^ Berry, Paul "APL\360 Primer Student Text", IBM Research, Thomas J. Watson Research Center, 1969.
- ^ "Treatise" (PDF). www.cs.utexas.edu. Retrieved 2019-09-10.
- ^ Cason, Stan. "APL2 Idioms Library". www-01.ibm.com. IBM. Retrieved 1 February 2015.
- ^ APL의 "하이 마이너스"는 이어지는 단일 번호에 적용되며, 모노딕 마이너스 함수는 전체 배열의 기호를 오른쪽으로 변경합니다.
- ^ "The Workspace - System Functions". Microapl.co.uk. p. (toward bottom of the web page). Retrieved 2018-11-05.
- ^ "APL language reference" (PDF). Retrieved 2018-11-05.
- ^ 유니코드 차트
외부 링크
- APL 문자 참조: 페이지 1, 페이지 2, 페이지 3, 페이지 4
- British APL Association 글꼴 페이지
- IBM 코드 페이지 293 메인프레임의 APL 코드 페이지라고도 합니다.
- APL Wiki의 APL 문자에 대한 일반 정보
- APL 및 그 키보드 기호 연산자를 확장합니다.
- Lee, Xah. "How to Create an APL or Math Symbols Keyboard Layout". Retrieved 13 January 2015.
일반적인 온라인 튜토리얼
- Graeme Donald Robertson의 APL 1과 APL 2에 대한 실용적인 소개
- PC, 서버 및 태블릿용 APL - NARS 풀기능, 제한 없음, 다운로드 가능한 APL/2(네스트된 어레이 포함) (Sudley Place 소프트웨어)
- GNU APL 무료 다운로드 가능 인터프리터 by 위르겐 사우어만
- 박지민이 올린 유튜브 APL 튜토리얼, 8개의 인트로/초급 지도 동영상.
- SIGAPL 컴파일 튜토리얼리스트
- APL 학습: Micro APL의 APL 튜토리얼
구문 규칙
- Conway's Game Of Life in APL, YouTube에서 진행
- Iverson, Kenneth E. (1983). "APL syntax and semantics". ACM SIGAPL APL Quote Quad. 13 (3): 223–231. doi:10.1145/800062.801221. ISBN 978-0897910958.
- Gffer, M. (1989). "A Future APL: Examples and Problems". ACM SIGAPL APL Quote Quad. 19 (4): 158–163. doi:10.1145/75144.75166. ISBN 978-0897913270.