AVL 트리

AVL 트리
AVL 트리
유형	트리
발명된	1962
발명자	게오르기 아델슨 벨스키와 에브게니 란디스
빅 O 표기의 시간 복잡도
알고리즘.
알고리즘.
공간
서치
삽입
삭제

AVL 트리에 여러 요소를 삽입하는 모습을 보여주는 애니메이션입니다.왼쪽, 오른쪽, 왼쪽-오른쪽 및 오른쪽-왼쪽 회전이 포함됩니다.

그림 1: 밸런스 팩터가 있는 AVL 트리(녹색)

컴퓨터 과학에서 AVL 트리(발명자 Adelson-Velsky와 Landis의 이름을 따서 이름 지어짐)는 자기 밸런싱 바이너리 검색 트리(BST)입니다.이러한 데이터 구조가 ^[2]발명된 것은 이번이 처음이었다.AVL 트리에서는 임의의 노드의 2개의 서브트리의 높이가 최대 1개씩 다릅니다.두 서브트리가 여러 개 다를 경우 이 속성을 복원하기 위해 재밸런싱이 실행됩니다.검색, 삽입 및 삭제에는 평균 및 최악의 경우 모두 O $(log$ n $)$ 시간이 $걸립니다$ . $n$ 서 n{\ $displaystyle$ n $}$ 은 $n$ 작업 전 트리 내 노드 수입니다.삽입 및 삭제 시 트리를 1회 이상 회전시켜 균형을 재조정해야 할 수 있습니다.

AVL 트리의 이름은 1962년 논문 "정보 조직을 위한 알고리즘"^[3]에 발표한 소련 발명가 게오르기 아델슨-벨스키와 에브게니 랜디스의 이름을 따 지어졌다.

AVL 트리는 같은 조작 세트를 지원하며 O ${\text{O}}(\log n)$ $)$ style(\ $displaystyle\text)$ 를 ${\text{O}}(\log n)$ 하기 때문에 종종 빨간색-검은색 트리와 비교됩니다. $O}}(\log$ n $)}$ 기본 ${\text{O}}(\log n)$ 작업에 대한 시간입니다.룩업 부하가 높은 애플리케이션의 경우 AVL 트리는 보다 엄밀하게 ^[4]균형 잡힌 상태이기 때문에 빨간색-검은색 트리보다 빠릅니다.AVL 트리는 빨강-검은색 트리와 마찬가지로 높이 균형이 잡혀 있습니다.일반적으로 둘 다 μ $\mu \leq {\tfrac {1}{2}}$ $\mu \leq {\tfrac {1}{2}}$ 2 \ $displaystyle$ \ $mu$ \ $leq$ { $tfrac {1}$ ${$ 2 $}$ ^[5]에 대해 무게 $\mu$ 도 $\mu$ μ \ $displaystyle$ \ $mu$ $\mu \leq {\tfrac {1}{2}}$ } 균형도 $\mu$ 아닙니다. 즉, 형제 노드의 후손 수는 크게 다를 수 있습니다.

정의.

밸런스 팩터

이진 트리에서 노드 X의 균형 계수는 높이 차이로 정의됩니다.

\displaystyle\text{BF}}(X): = 텍스트{높이}}({\text{RightSubtree}}(X)-{\text{높이}}({\text{Left Subtree}}(X))}

^[6]^{: 459}

두 아이 중 한 명이에요바이너리 트리는 불변인 경우 AVL 트리로 정의됩니다.

\displaystyle\text{BF}}(X)\in {-1,0,1\}

^[7]

는 트리 내의 모든 노드 X에 대해 유지됩니다.

${\text{BF}}(X)<0$ 가 ${\text{BF}}(X)<0$ 있는 노드 X ( ${\text{BF}}(X)<0$ ) < ${\text{BF}}(X)<0$ \ $displaystyle$ \ $text$ { $B$ ） $F}}(X)<0}$ 은 ${\text{BF}}(X)<0$ BF( ${\text{BF}}(X)>0$ (\ $displaystyle\text{B$ })으로 "왼쪽 무게"라고 불립니다.F $}}(X)>0}$ 은 ${\text{BF}}(X)>0$ "오른쪽 무게"라고 불리며 ${\text{BF}}(X)=0$ BF $)=$ $(\displaystyle\text$ {B)인 것이 1개 $있습니다$ . $F}}(X)=0}$ 을 ${\text{BF}}(X)=0$ (를) 단순히 "균형"이라고 부르기도 합니다.

특성.

밸런스 팩터는 이전 밸런스 팩터와 높이 변화를 알면 최신 상태를 유지할 수 있습니다.절대 높이를 알 필요는 없습니다.AVL 밸런스 정보를 유지하기 위해서는 노드당 2비트로 ^[8]충분합니다.

n개의 $n$ $노드$ 를 $가진$ AVL 트리의 $높이$ h $($ $최대$ 레벨 수로 카운트)는 다음과 ^[6]^{: 460}같습니다.

\displaystyle \log _{2}(n+1)\leq h <\log _{\varphi }(n+2)+b}

여기서 $\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618$ : $\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618$ 1 + $\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618$ 2 $\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618$ $\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618$ . $display$ style \ $varphi$ : = $displaytfrac$ { $1$ + { \ $rt$ { $5$ } { } { } { $b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.$ $11$ b : $b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.$ $b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.$ 2 $b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.$ $b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.$ $b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.$ 2 $b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.$ - $b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.$ $b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.$ - $b:={\frac {\log _{2}5}{2\log _{2}\varphi }}-2\approx \;-0.3277.$ - $= frac log _$ ${ 2$ } { 2 } { \ $displaystylog$ { 2 } { 2 } { \ $displaystyparb$ } { \ log { 2 } 에는 적어도 $F_{h}-1$ - $F_{h}-1$ {\ $displaystyle F_{h}-1}개$ 의 $F_{h}-1$ 노드가 포함되어 있습니다 $\{F_{n}\}_{n\in \mathbb {N} }$ 서 { $\{F_{n}\}_{n\in \mathbb {N} }$ $\{F_{n}\}_{n\in \mathbb {N} }$ $\{F_{n}\}_{n\in \mathbb {N} }$ {\ $\{F_{n}\}_{n\in \mathbb {N} }$ ${\$ { $N}}}}}$ 은 $\{F_{n}\}_{n\in \mathbb {N} }$ $F_{1}=F_{2}=1.$ 값 $F_{1}=F_{2}=1.$ $= 1의 피보나치 시퀀스입니다.$ $}$

운용

AVL 트리의 읽기 전용 조작에는 언밸런스 바이너리 검색 트리에서 실행되는 것과 같은 액션을 실행하는 것이 포함되지만, 변경에서는 서브 트리의 높이 밸런스를 관찰하고 복원해야 합니다.

검색 중

AVL 트리에서 특정 키를 검색하는 것은 균형 또는 불균형 바이너리 검색 ^[9]^{: ch. 8}트리와 동일한 방법으로 수행할 수 있습니다.검색이 효과적으로 작동하려면 ^[10]^{: 23}키 집합의 전체 순서(또는 적어도 전체 사전 순서)를 설정하는 비교 함수를 사용해야 합니다.성공적인 검색에 필요한 비교 횟수는 $높이$ h에 의해 제한되며 실패한 검색의 $경우$ h에 매우 가깝기 때문에 둘 다 O $($ ^[11]^{: 216}log $n$ )에 있습니다.

트래버설

읽기 전용 조작으로서 AVL 트리의 트래버설은 다른 바이너리 트리와 동일하게 기능합니다.트리의 $모든$ n개 노드를 탐색하면 각 링크가 정확히 두 번 방문됩니다.하향 방문은 해당 노드에 의해 루트된 서브트리에 들어가기 위한 것이고, 다른 방문은 해당 노드의 서브트리를 탐색한 후에 떠나기 위한 것입니다.

AVL 트리에서 노드가 발견되면 다음 노드 또는 이전 노드에 상각된 상수 ^[12]^{: 58}시간 내에 액세스할 수 있습니다.이러한 "근접" 노드를 탐색하는 일부 인스턴스에서는 $최대$ $h개의$ log $(n)$ 링크를 통과해야 합니다(특히 루트의 왼쪽 서브트리의 오른쪽 끝 리프 또는 루트의 오른쪽 서브트리의 왼쪽 리프에서 루트로 이동하는 경우).그림 1의 AVL 트리에서 노드 P에서 오른쪽 옆 노드로 이동하는 경우 Q3 절차를 수행합니다).어느 트리에나 $n-1$ 링크가 있기 때문에 $상각비용$ 은 2 $\times(n-1)/ n$ , 즉 약 2입니다.

삽입

노드를 AVL 트리에 삽입할 때는 처음에 바이너리 검색 트리에 삽입하는 것과 같은 프로세스를 수행합니다.트리가 비어 있으면 노드가 트리의 루트로 삽입됩니다.트리가 비어 있지 않으면 루트로 이동하여 새 노드를 삽입할 위치를 반복적으로 찾습니다.이 통과는 비교 함수에 의해 유도됩니다.이 경우 노드는 항상 트리의 외부 노드의 NULL 참조(왼쪽 또는 오른쪽)를 대체한다.즉, 노드는 외부 노드의 왼쪽 자식 또는 오른쪽 자식 중 하나가 된다.

이 삽입 후 트리가 불균형 상태가 되면 새로 삽입된 노드의 상위 노드만 불균형 상태가 됩니다.이는 이러한 노드만 하위 트리가 ^[13]변경되기 때문입니다.따라서 각 노드의 상위 노드가 AVL 트리의 불변성과 일관성을 유지하는지 확인해야 합니다. 이를 "역추적"이라고 합니다.이는 각 ^[6]^{: 458–481}노드의 밸런스 계수를 고려함으로써 실현됩니다.^[12]^{: 108}

1개의 삽입으로 AVL 서브트리의 높이를 1개 이상 늘릴 수 없기 때문에 삽입 후 노드의 일시적인 밸런스 계수는 [–2,+2]의 범위에 있습니다.체크된 각 노드에 대해 임시 밸런스 계수가 –1 ~ +1 범위에 있으면 밸런스 계수만 업데이트되고 회전은 필요하지 않습니다.다만, 일시 밸런스 계수가 ±2인 경우, 이 노드에 루트가 있는 서브 트리는 AVL 언밸런스이며,^[10]^{: 52} 회전이 필요합니다.아래 코드와 같이 삽입하면 적절한 회전이 즉시 트리의 균형을 완벽하게 재조정합니다.

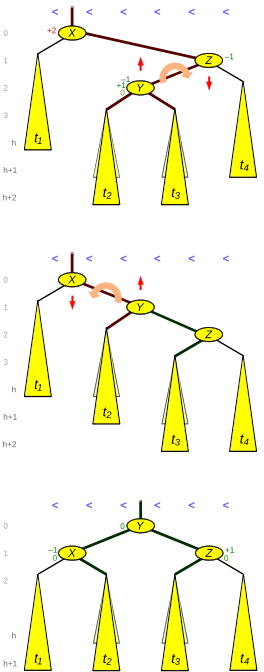
그림 1에서는 노드 X의 자녀로서 새로운 노드 Z를 삽입함으로써 그 서브트리 Z의 높이가 0에서 1로 증가한다.

삽입용 역추적 루프의 불변성

Z에 의해 루트된 서브트리의 높이가 1 증가했습니다.그것은 이미 AVL 형태입니다.

삽입 작업의 예제 코드

위해서 (X = 부모(Z); X != 무효; X = 부모(Z)) { // 루프(루트까지 가능)     // BF(X)를 업데이트해야 합니다.     한다면 (Z == 오른쪽 아이(X)) { // 오른쪽 서브트리가 증가합니다.         한다면 (BF(X) > 0) { // X는 오른쪽 무게입니다.             // == > 임시 BF(X) == +2             // == > 재밸런싱이 필요합니다.             G = 부모(X); // 회전 주위에 X의 부모 저장             한다면 (BF(Z) < > 0)                  // 오른쪽 왼쪽 케이스(그림 3 참조)                 N = rotate_오른쪽 왼쪽(X, Z); // 이중 회전:오른쪽(Z), 왼쪽(X)             또 다른                            // 오른쪽 케이스(그림2 참조)                 N = 회전_왼쪽(X, Z);      // 좌측 단일 회전(X)             // 회전 후 부모 링크 적용         } 또 다른 {             한다면 (BF(X) < > 0) {                 BF(X) = 0; // Z의 높이 상승은 X에서 흡수됩니다.                 브레이크.; // 루프를 종료합니다.             }             BF(X) = +1;             Z = X; // 높이(Z)가 1 증가             계속하다.;         }     } 또 다른 { // Z == left_child(X): 왼쪽 하위 트리가 증가합니다.         한다면 (BF(X) < > 0) { // X는 왼쪽이 무겁습니다.             // == > 임시 BF(X) == - 2             // == > 재밸런싱이 필요합니다.             G = 부모(X); // 회전 주위에 X의 부모 저장             한다면 (BF(Z) > 0)                  // 왼쪽 대문자                 N = rotate_왼쪽(X, Z); // 이중 회전:왼쪽(Z), 오른쪽(X)             또 다른                            // 왼쪽 대문자                 N = 회전_오른쪽(X, Z);     // 단일 회전 오른쪽(X)             // 회전 후 부모 링크 적용         } 또 다른 {             한다면 (BF(X) > 0) {                 BF(X) = 0; // Z의 높이 상승은 X에서 흡수됩니다.                 브레이크.; // 루프를 종료합니다.             }             BF(X) = -1;             Z = X; // 높이(Z)가 1 증가             계속하다.;         }     }     // 회전 후 부모 링크 적용:     // N은 회전된 서브트리의 새 루트입니다.     // 높이가 변경되지 않음:높이(N) == 이전 높이(X)     부모(N) = G;     한다면 (G != 무효) {         한다면 (X == 왼쪽_자녀(G))             왼쪽_자녀(G) = N;         또 다른             오른쪽 아이(G) = N;     } 또 다른         트리->뿌리 = N; // N은 전체 트리의 새 루트입니다.     브레이크.;     // 폴트 스루는 없고, 브레이크만 있거나, 계속합니다. } // 루프가 중단되지 않는 한 전체 트리의 높이는 1 증가합니다.

모든 노드의 밸런스 계수를 업데이트하려면 먼저 삽입된 리프 경로를 따라 보정이 필요한 모든 노드가 자식에서 부모로 있는지 확인합니다.위의 절차를 리프부터 시작하여 이 경로를 따라 노드에 적용하면 트리 내의 모든 노드에 다시 -1, 0 또는 1의 밸런스 계수가 부여됩니다.

균형 계수가 0이 되면 역추적이 중지되어 해당 서브트리의 높이가 변경되지 않습니다.

밸런스 계수가 ±1이 되면 서브트리의 높이가 1씩 증가하므로 역추적이 계속되어야 합니다.

밸런스 계수가 일시적으로 ±2가 되면 서브트리가 이전과 같은 높이(및 그 루트 밸런스 계수 0)를 갖는 적절한 회전에 의해 수리해야 한다.

필요한 시간은 룩업에 $O$ ( $log$ n $)$ 와 루트 복귀 시 최대 O $(log$ n $)$ 재트레이싱 수준( $평균$ O(1 $))$ 이므로 O $(log$ n $)$ ^[10]^{: 53} 시간 내에 $작업$ 을 완료할 수 있습니다.

삭제

노드를 삭제하는 예비 단계는 이진 검색 트리 #삭제 섹션에 설명되어 있습니다.여기서 서브젝트 노드 또는 치환 노드의 효과적인 삭제는 대응하는 서브트리의 높이를 1에서 0으로, 또는 서브노드가 있으면 2에서 1로 낮춘다.

이 서브트리에서 시작하여 AVL 트리의 불변성과의 일관성을 각 상위 트리에서 확인할 필요가 있습니다.이것을 "역추적"이라고 합니다.

1회의 삭제로 AVL 서브트리의 높이를 1개 이상 줄일 수 없기 때문에 노드의 일시적인 밸런스 팩터는 -2 ~+2 의 범위입니다.밸런스 팩터가 -1 ~+1 의 범위에 머무르고 있는 경우는, AVL 규칙에 따라서 조정할 수 있습니다.±2가 되면 서브트리가 불균형하므로 회전해야 합니다.(회전이 항상 트리의 균형을 잡는 삽입과 달리 삭제 후에는 BF(Z) 0 0(그림 2 및 3 참조)이 있을 수 있습니다.따라서 적절한 단일 또는 이중 회전 후 재조정된 서브트리의 높이가 한 가지 감소하므로 트리는 다음 상위 레벨에서 다시 균형을 맞춰야 합니다.)다양한 회전 사례에 대해서는 재조정 섹션에 설명되어 있습니다.

삭제용 역추적 루프의 불변성

N에 의해 루트된 서브트리의 높이가 1 감소했습니다.그것은 이미 AVL 형태입니다.

삭제 작업 예제 코드

위해서 (X = 부모(N); X != 무효; X = G) { // 루프(루트까지 가능)     G = 부모(X); // 회전 주위에 X의 부모 저장     // BF(X)가 아직 업데이트되지 않았습니다!     한다면 (N == 왼쪽_자녀(X)) { // 왼쪽 서브트리가 감소합니다.         한다면 (BF(X) > 0) { // X는 오른쪽 무게입니다.             // == > 임시 BF(X) == +2             // == > 재밸런싱이 필요합니다.             Z = 오른쪽 아이(X); // N의 형제(2만큼 높음)             b = BF(Z);             한다면 (b < > 0)                      // 오른쪽 왼쪽 케이스(그림 3 참조)                 N = rotate_오른쪽 왼쪽(X, Z); // 이중 회전:오른쪽(Z), 왼쪽(X)             또 다른                            // 오른쪽 케이스(그림2 참조)                 N = 회전_왼쪽(X, Z);      // 좌측 단일 회전(X)             // 회전 후 부모 링크 적용         } 또 다른 {             한다면 (BF(X) == 0) {                 BF(X) = +1; // N의 높이 감소는 X에서 흡수됩니다.                 브레이크.; // 루프를 종료합니다.             }             N = X;             BF(N) = 0; // 높이(N)가 1 감소합니다.             계속하다.;         }     } 또 다른 { // (N == right_child(X):오른쪽 서브트리가 감소합니다.         한다면 (BF(X) < > 0) { // X는 왼쪽이 무겁습니다.             // == > 임시 BF(X) == - 2             // == > 재밸런싱이 필요합니다.             Z = 왼쪽_자녀(X); // N의 형제(2만큼 높음)             b = BF(Z);             한다면 (b > 0)                      // 왼쪽 대문자                 N = rotate_왼쪽(X, Z); // 이중 회전:왼쪽(Z), 오른쪽(X)             또 다른                            // 왼쪽 대문자                 N = 회전_오른쪽(X, Z);     // 단일 회전 오른쪽(X)             // 회전 후 부모 링크 적용         } 또 다른 {             한다면 (BF(X) == 0) {                 BF(X) = -1; // N의 높이 감소는 X에서 흡수됩니다.                 브레이크.; // 루프를 종료합니다.             }             N = X;             BF(N) = 0; // 높이(N)가 1 감소합니다.             계속하다.;         }     }     // 회전 후 부모 링크 적용:     // N은 회전된 서브트리의 새 루트입니다.     부모(N) = G;     한다면 (G != 무효) {         한다면 (X == 왼쪽_자녀(G))             왼쪽_자녀(G) = N;         또 다른             오른쪽 아이(G) = N;     } 또 다른         트리->뿌리 = N; // N은 전체 트리의 새 루트입니다.       한다면 (b == 0)         브레이크.; // 높이가 변경되지 않음:루프를 남기다       // 높이(N)가 1 감소(== 이전 높이(X)-1) } // (b!= 0)인 경우 전체 트리의 높이가 1 감소합니다.

균형 계수가 ±1(0이어야 함)이 되면 역추적이 중지될 수 있습니다. 즉, 하위 트리의 높이가 변경되지 않습니다.

밸런스 계수가 0이 되면(±1이어야 함) 서브트리의 높이가 1 감소하므로 역추적이 계속되어야 합니다.

밸런스 계수가 일시적으로 ±2가 되면 적절한 회전을 통해 수리해야 합니다.하위 트리의 높이가 1 감소하는지(그림 2의 상위 하위 트리) 또는 역추적이 계속되어야 하는지 또는 변화하지 않는지(Z의 균형 계수 0인 경우) 형제 Z의 균형 계수에 따라 전체 트리가 AVL 모양이다.

필요한 시간은 룩업에 $O$ ( $log$ n $)$ 와 루트 복귀 시 최대 O $(log$ n $)$ 재트레이싱 수준( $평균$ O(1 $))$ 이므로 O $(log$ n $)$ 시간 내에 $작업$ 을 완료할 수 있습니다.

작업 및 대량 작업 설정

단일 요소 삽입, 삭제 및 조회 조작 외에 AVL 트리에는 결합, 교차 및 설정 차이와 같은 몇 가지 설정 조작이 정의되어 있습니다.그 후, 이러한 설정 기능에 근거해 삽입 또는 삭제시의 고속 벌크 조작을 실장할 수 있습니다.이러한 세트 조작은, 2개의 헬퍼 조작(스플릿 조작과 참가 조작)에 의존합니다.새로운 운용에 의해, AVL 트리의 실장은 보다 효율적이고,^[14] 고도의 병렬화가 가능하게 됩니다.

2개의 AVL $트리 1$ t와 $t 2$ $및$ 키 k에 대한 Join 함수는 $k뿐$ 만 아니라 t, $t$ 의₂ $모든 1$ 요소를 포함하는 트리를 반환합니다.k는 $t$ 의₁ 모든 키보다 크고 t의 $모든 2$ 키보다 작아야 $합니다$ .2개의 트리가 최대 1개의 높이에 따라 다를 경우 조인(Join)은 왼쪽 $서브트리 1$ t, $루트$ k 및 오른쪽 $서브트리 2$ t를 사용하여 새 노드를 만듭니다.그렇지 않으면 둘 이상의 $경우$ 에₁ 대해 t가 $t$ 보다₂ 높다고 가정합니다(다른 경우에는 대칭).조인(join)은 t와 $균형$ 을₂ 이루는 $노드$ c가 될 $때$ 까지₁ t의 오른쪽 척추를 따릅니다.이 시점에서 c를 대체할 왼쪽 자식 c, $루트$ k 및 오른쪽 $자식 2$ t를 $가진$ 새로운 노드가 생성됩니다.새로운 노드는 AVL 불변수를 충족하며, 그 높이는 c보다 $큽니다$ .높이가 증가하면 이전 노드의 높이가 증가하여 이러한 노드의 AVL 불변성이 무효가 될 수 있습니다.부모에서 비활성화된 경우 이중 회전으로 고정하거나 트리에서 더 높은 위치에 비활성화된 경우 왼쪽 단일 회전으로 고정할 수 있으며, 두 경우 모두 상위 노드의 높이를 복원합니다.따라서 조인에는 최대 2회 회전이 필요합니다.이 함수의 비용은 두 입력 트리 사이의 높이 차이입니다.

Join 알고리즘의 의사 코드 실장

함수 JoinRightAVL(T_L, k, T_R)(l,k',c) = 노출(T_L)인 경우(높이(c) <= 높이(T_R)+1) T' = 노드(c,k,T_R)인 경우(높이(T') <= 높이(l)+1)가 반환된 경우, 그렇지 않으면 노드(k')AVL(c,k,T_R) T' = 노드(l,k',T')가 (높이(T') <= 높이(l)+1)가 T'를 반환하고, 그렇지 않으면 회전 왼쪽(T')이 반환됩니다.

JoinLeftAVL(T_L, k, T_R) /* 함수는 JoinRight와 대칭입니다.AVL */

함수_R 가입(T_L, k, T) if (높이(T_L) >높이(T_R)+1)가 Join RightAVL_R(T_L, k, T)를 반환한다(높이_R(T) >높이(T_L)+1)가 JoinLeftAVL(T_L, k, T_R_R)을_L 반환한다.

여기서 높이(v)는 하위 트리(노드) $v$ . (l,k,r) = 노출(v) $추출$ v의 왼쪽 $자식$ l, v의 $루트$ $키$ k 및 오른쪽 $자식$ r.노드(l,k,r)는 왼쪽 $아이$ l, 키 $k$ 및 오른쪽 $아이$ r의 노드를 작성하는 것을 의미합니다.

AVL 트리를 2개의 작은 트리( $키$ k보다 작은 트리 및 $키$ k보다 큰 트리)로 분할하려면 먼저 AVL에 k를 $삽입$ 하여 루트에서 경로를 그립니다.이 삽입 후 경로 왼쪽에 k보다 $작은$ 값이 모두 표시되고 오른쪽에 $k$ 보다 큰 값이 모두 표시됩니다.Join을 적용하면 패스의 키를 아래에서 위로 중간 노드로 하여 왼쪽의 모든 서브트리가 아래쪽에서 위로 병합되어 왼쪽 트리가 형성되고 오른쪽 부분이 비대칭이 됩니다.분할 비용은 O $(log$ n $)$ 로 트리 $높이$ 의 순서입니다.

스플릿 알고리즘의 의사 코드 실장
(T = 0)이 반환되는 경우 함수 분할(T,k)(L,m,R) = 노출(T)이 반환되는 경우 (k = m)이 반환되는 경우(L',b,R') = 분할(L,k) 반환(L',R'join)

$세트$ $A$ 와 B를 나타내는2개의 AVL $트리 1$ $t$ 와₂ t의 결합은 A $b$ B를 $나타내는$ $AVL$ t입니다.

Union 알고리즘의 의사 코드 실장

함수 Union(t₁, t₂): t = 0인₂ 경우₁ t 반환₂: t(t_<, b, t_>)를 반환합니다₁. = 분할(t₂, t₁.root)을 반환합니다. Join(Union(왼쪽(t₁), t_<), t₁.root, Union(오른쪽(t₁), t)를_> 반환합니다.

여기서 Split은 2개의 트리를 반환하는 것으로 간주됩니다.하나는 입력 키보다 작은 키를 유지하고 다른 하나는 큰 키를 유지합니다.(알고리즘은 비파괴적이지만 임플레이스파괴 버전도 존재합니다).

교차 또는 차이에 대한 알고리즘은 비슷하지만 Join과 동일하지만 중간 키가 없는 Join2 도우미 루틴이 필요합니다.결합, 교차 또는 차이에 대한 새로운 기능에 따라 AVL 트리에 1개 또는 여러 개의 키를 삽입하거나 삭제할 수 있습니다.스플릿은 Join을 호출하지만 AVL 트리의 밸런싱 기준을 직접 다루지 않기 때문에, 이러한 실장은 통상 「join 베이스」의 실장이라고 불립니다.

$각$ 결합, 교차로 및 차이의 ${\text{O}}\left(m\log \left({n \over m}+1\right)\right)$ 는 O ${\text{O}}\left(m\log \left({n \over m}+1\right)\right)$ log ${\text{O}}\left(m\log \left({n \over m}+1\right)\right)$ ( ${\text{O}}\left(m\log \left({n \over m}+1\right)\right)$ ${\text{O}}\left(m\log \left({n \over m}+1\right)\right)$ + 1 $)\$ style { $display$ { text ${\text{O}}\left(m\log \left({n \over m}+1\right)\right)$ } $O$ $}}\$ $left(m\log$ $m$ \ $left({n \over$ m $}+1\right)$ 는 ${\text{O}}\left(m\log \left({n \over m}+1\right)\right)$ 크기가 m(\ $displaystyle$ m}) $n\;(\geq m)$ 및 n $)$ 인 AVL 트리의 경우(\ $displaystyle$ m)\ $display$ n $\;(\geq$ m $n\;(\geq m)$ right).더 중요한 것은 결합, 교차점 또는 차이에 대한 재귀 호출은 서로 독립적이므로 로그 ${\text{O}}(\log m\log n)$ 에서 ${\text{O}}(\log m\log n)$ 로 실행할 수 있습니다. $디스플레이$ $O}}(\log$ m $\log$ n ${\text{O}}(\log m\log n)$ ^[14]m $m=1$ $m=1$ { $displaystyle$ m= $1$ 의 $m=1$ , Join 베이스의 실장에서는, 단일 슬롯의 삽입 및 삭제와 같은 계산 DAG 가 사용됩니다.

재조정

수정 작업 중에 두 하위 트리 사이의 높이 차이가 변경되는 경우, 이 차이가 2 미만인 한 부모에서 균형 정보를 적용함으로써 반영될 수 있습니다.삽입 및 삭제 작업 중에 (일시) 높이 차이가 2가 발생할 수 있습니다. 즉, 상위 하위 트리를 "재균형"해야 합니다.지정된 복구 도구는 키를 "수직"으로만 이동하기 때문에 이른바 트리 회전입니다. 따라서 키의 순차적인("수평") 시퀀스가 완전히 보존됩니다(바이너리 검색 ^[6]^{: 458–481}트리에 필수적임).^[12]^{: 33}

X를 -2 또는 +2의 (일시) 균형 계수를 갖는 노드로 합니다.왼쪽 또는 오른쪽 서브트리가 변경되었습니다.Z를 큰 아이로 합니다(그림 2 및 3 참조).유도 가설에 의해 두 아이 모두 AVL 모양입니다.

삽입한 경우 Z의 자녀 중 한 명에게 키가 커진 상태로 삽입이 발생했습니다.삭제 시 이 삭제는 Z의 형제₁ t에 이미 t의 키가 낮아지는₁ 방식으로 발생하였습니다.(Z의 균형 계수도 0일 수 있는 유일한 경우입니다.)

위반에는 다음 4가지 종류가 있습니다.

그렇죠, 맞습니다.	§ Z는 오른쪽	부모 X 및 BF(Z)의 자녀 of 0
왼쪽	§ Z는 왼쪽	부모 X 및 BF(Z)의 자녀 of 0
오른쪽 왼쪽	§ Z는 오른쪽	부모 X 및 BF(Z)의 자녀 <0
왼쪽 오른쪽	§ Z는 왼쪽	부모 X 및 BF(Z)의 자녀> 0

또한 재조정은 다음과 같이 수행됩니다.

그렇죠, 맞습니다.	§ X는 a로 재조정됩니다.	간단하죠.	회전`rotate_Left`	(그림2 참조)
왼쪽	§ X는 a로 재조정됩니다.	간단하죠.	회전`rotate_Right`	(그림 2의 미러 이미지)
오른쪽 왼쪽	§ X는 a로 재조정됩니다.	이중으로 하다	회전`rotate_RightLeft`	(그림3 참조)
왼쪽 오른쪽	§ X는 a로 재조정됩니다.	이중으로 하다	회전`rotate_LeftRight`	(그림 3의 미러 이미지)

따라서 상황은 C B로 표시되며, 여기서 C(= 자방향)와 B(= 균형)는 Right := -Left로 설정된 {Left, Right }에서 나온다.케이스 C == B의 밸런스 위반은 단순 회전(-C)으로 수리하고 케이스 C != B는 이중 회전 CB로 수리한다.

회전 비용은 단순 또는 이중으로 일정합니다.

심플 로테이션

그림 2는 오른쪽 상태를 나타내고 있습니다.노드 X의 윗부분에는 밸런스 계수가 +2인 2개의 자 트리가 있습니다.또한 Z의 내측 아이₂₃ t(즉, Z가 오른쪽 아이 respon일 경우 왼쪽 아이)이다.오른쪽 아이(Z가 왼쪽 아이일 때)가 형제₄ t보다 높지 않습니다.이는 서브트리₄ t의 높이 증가 또는 서브트리₁ t의 높이 감소에 의해 발생할 수 있습니다.후자의 경우 t가 t와 같은₄ 높이를 갖는 창백한₂₃ 상황도 발생할 수 있습니다.

왼쪽 회전의 결과는 그림 아래쪽에 나와 있습니다.3개의 링크(그림2의 두꺼운 가장자리)와 2개의 밸런스 팩터를 갱신합니다.

그림과 같이 잎층은 삽입 전 레벨 h+1, 일시적으로 레벨 h+2, 그리고 다시 회전 후 레벨 h+1이었다.결실의 경우 t와₄ t의 높이가 같았을 때₂₃ 잎층은 다시 h+2 수준이었다.그렇지 않으면 잎층이 레벨 h+1에 도달하여 회전된 트리의 높이가 감소합니다.

그림 2: 단순 회전
회전_좌(X,Z)

단순 좌회전 코드 조각

입력:	X = 왼쪽으로 회전할 하위 트리의 루트
	Z = X의 오른쪽 자식, Z는 오른쪽 무게입니다.
	높이 == $높이(LeftSubtree($ X $)+2$ 인 경우
결과:	재조정된 하위 트리의 새 루트

노드 *회전_왼쪽(노드 *X, 노드 *Z) {     // Z가 형제보다 2 더 높습니다.     t23 = 왼쪽_자녀(Z); // Z의 내부 자식     오른쪽 아이(X) = t23;     한다면 (t23 != 무효)         부모(t23) = X;     왼쪽_자녀(Z) = X;     부모(X) = Z;     // 첫 번째 케이스, BF(Z) == 0,     // 삭제 시에만 발생하며 삽입되지 않습니다.     한다면 (BF(Z) == 0) { // t23은 t4와 같은 높이입니다.         BF(X) = +1;   // t23이 높아졌습니다.         BF(Z) = –1;   // T4가 X보다 낮아졌습니다.     } 또 다른     { // 삽입 또는 삭제 시 두 번째 케이스 발생:         BF(X) = 0;         BF(Z) = 0;     }     돌아가다 Z; // 회전된 하위 트리의 새 루트를 반환합니다. }

이중 회전

그림 3은 우측 좌측 상황을 나타내고 있습니다.노드 X의 위쪽 세 번째 부분에는 밸런스 계수가 +2인 2개의 자식 트리가 있습니다.그러나 그림 2와 달리 Z의 내부 자식 Y는 형제₄ t보다 높습니다.이는 Y 자체의 삽입이나 하위 트리₂ t 또는₃ t의 높이 증가(그 결과 높이가 다름) 또는 하위 트리₁ t의 높이 감소에 의해 발생할 수 있습니다.후자의 경우 t와₃ t의 높이가 같을 수도₂ 있습니다.

첫 번째 오른쪽 회전 결과는 그림의 중간 1/3에 나타나 있습니다(밸런스 계수에 관해서는 Y와₄ t의 높이 차이가 1에 불과하기 때문에 이 회전은 다른 AVL 단일 회전과 동일하지 않습니다).마지막 왼쪽 회전 결과는 그림의 아래쪽 1/3에 나와 있습니다.5개의 링크(그림3의 두꺼운 가장자리)와 3개의 밸런스 팩터를 갱신합니다.

그림과 같이 잎층은 삽입 전 레벨 h+1로 일시적으로 레벨 h+2로, 다시 레벨 h+1로 더블 회전한 후 레벨 h+1로 되어 있었다.결실의 경우 잎층은 h+2레벨로, 이중회전 후에는 h+1레벨로 회전하는 나무의 높이가 감소한다.

그림 3: 2회전 회전_우측좌측(X,Z)
= 회전_Z 주위를 오른쪽으로 돌린 후 그 다음
회전_X 주위를 왼쪽으로 돌다

오른쪽-왼쪽 이중 회전 코드 조각

입력:	X = 회전할 서브트리의 루트
	Z = 오른쪽 자식, 왼쪽 무게
	높이 == $높이(LeftSubtree($ X $)+2$ 인 경우
결과:	재조정된 하위 트리의 새 루트

노드 *rotate_오른쪽 왼쪽(노드 *X, 노드 *Z) {     // Z가 형제보다 2 더 높습니다.     Y = 왼쪽_자녀(Z); // Z의 내부 자식     // Y가 형제보다 1 높음     t3 = 오른쪽 아이(Y);     왼쪽_자녀(Z) = t3;     한다면 (t3 != 무효)         부모(t3) = Z;     오른쪽 아이(Y) = Z;     부모(Z) = Y;     t2 = 왼쪽_자녀(Y);     오른쪽 아이(X) = t2;     한다면 (t2 != 무효)         부모(t2) = X;     왼쪽_자녀(Y) = X;     부모(X) = Y;     // 첫 번째 케이스, BF(Y) == 0,     // 삭제 시에만 발생하며 삽입되지 않습니다.     한다면 (BF(Y) == 0) {         BF(X) = 0;         BF(Z) = 0;     } 또 다른     // 삽입 또는 삭제 시 다른 경우가 발생합니다.         한다면 (BF(Y) > 0) { // t3가 더 높음             BF(X) = –1;  // t1이 높아졌습니다.             BF(Z) = 0;         } 또 다른 {             // t2가 더 높음             BF(X) = 0;             BF(Z) = +1;  // t4가 높아졌습니다.         }     BF(Y) = 0;     돌아가다 Y; // 회전된 하위 트리의 새 루트를 반환합니다. }

다른 구조물과의 비교

AVL 트리와 빨간색-검은색(RB) 트리는 모두 자가 밸런싱 바이너리 검색 트리이며 수학적으로 관련이 있습니다.실제로, 모든 AVL 트리는 ^[15]빨강-검정색으로 색칠할 수 있지만, AVL 밸런스가 맞지 않는 RB 트리가 있습니다.AVL 응답을 유지하기 위해서.RB 트리의 불변성, 회전은 중요한 역할을 합니다.최악의 경우 회전하지 않아도 AVL 또는 RB 삽입 또는 삭제 시 O $(log$ n $)$ 검사 및/또는 AVL 밸런스 팩터 응답 $업데이트$ 가 필요합니다.RB 컬러.RB 삽입 및 삭제 및 AVL 삽입에는 0~3회 테일 재귀 회전이 필요하며 $상각된$ O(1) $시간$ ^[16]^{: pp.165, 158}내에 실행되므로 평균 일정합니다.최악의 경우 O $(log$ n $)$ 회전이 $필요$ 한 AVL 결손도 $평균$ O(1)입니다 $.$ RB 트리는 각 노드에 1비트의 정보(색상)를 저장해야 하지만 AVL 트리는 대부분 밸런스 팩터로 2비트를 사용합니다.단, 자녀에게 저장되는 경우에는 "형제보다 낮은" 의미를 가진 1비트로 충분합니다.두 데이터 구조 간의 큰 차이는 높이 제한입니다.

$크기$ 가 n $1$ 1인 트리의 경우

AVL 트리의 높이는 최대
${\displaystyle{array}{ll}h&\leq \;c\log _{2}(n+d)+b\\&<\c\log_{2}(n+2)+b\end{array}}$

c:={\tfrac {1}{\log _{2}\varphi }}\approx 1.440,

서

\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618

:

\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618

\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618

+

\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618

\varphi :={\tfrac {1+{\sqrt {5}}}{2}}\approx 1.618

.

displaystyle

\

varphi

:

c:={\tfrac {1}{\log _{2}\varphi }}\approx 1.440,

displaytfrac

{ 1 + { \

log

rt {

5

c:={\tfrac {1}{\log _{2}\varphi }}\approx 1.440,

{ } { } { } { } {

c:={\tfrac {1}{\log _{2}\varphi }}\approx 1.440,

1.

c:={\tfrac {1}{\log _{2}\varphi }}\approx 1.440,

{

c:={\tfrac {1}{\log _{2}\varphi }}\approx 1.440,

displaystyle

c:={\tfrac {1}{\log _{2}\varphi }}\approx 1.440,

: =

displaytfrac { 1

} { \ 2 } \

varphi

}

。

\;-0.328,}

및

b:={\tfrac {c}{2}}\log _{2}5-2\approx \;-0.328,

d:=1+{\tfrac {1}{\varphi ^{4}{\sqrt {5}}}}\approx 1.065

d :

=

+

d:=1+{\tfrac {1}{\varphi ^{4}{\sqrt {5}}}}\approx 1.065

d:=1+{\tfrac {1}{\varphi ^{4}{\sqrt {5}}}}\approx 1.065

5

d:=1+{\tfrac {1}{\varphi ^{4}{\sqrt {5}}}}\approx 1.065

1.

d:=1+{\tfrac {1}{\varphi ^{4}{\sqrt {5}}}}\approx 1.065

{

displaystyle

d:=

1+{\tfrac {1}{\varphi ^{4}{\

varphi rt

{5}}}}}\약 1.065

RB 트리의 높이는 기껏해야 이다
${\begin{array}{ll}h&\leqq \;2\log _{2}(n+1)\end{array}}$ 2 ${\begin{array}{ll}h&\leqq \;2\log _{2}(n+1)\end{array}}$ 2 ${\begin{array}{ll}h&\leqq \;2\log _{2}(n+1)\end{array}}$ （ ${\begin{array}{ll}h&\leqq \;2\log _{2}(n+1)\end{array}}$ + ${\begin{array}{ll}h&\leqq \;2\log _{2}(n+1)\end{array}}$ ）{ $displaystyle$ { $array }h&\leq$ \ ; 2 \ $log$ _ { $2}$ ( $n$ + $1$ ) \ $end$ { array ${\begin{array}{ll}h&\leqq \;2\log _{2}(n+1)\end{array}}$ } ${\begin{array}{ll}h&\leqq \;2\log _{2}(n+1)\end{array}}$ ^[18]} 。

AVL 트리는 최대 높이의 점근 관계 AVL/RB ≤ 0.720을 갖는 RB 트리보다 더 견고하게 균형 잡혀 있다.삽입과 결실의 경우, Ben Paff는 79회 측정에서 중앙값이 0.947이고 기하 평균이 0.910인 ^[4]0.677과 1.077 사이의 AVL/RB 관계를 보여준다.

「」를 참조해 주세요.

레퍼런스

^ ^a ^b ^c ^d ^e ^f Eric Alexander. "AVL Trees". Archived from the original on July 31, 2019.{{cite web}}: CS1 유지보수: 부적합한 URL(링크)
^ Sedgewick, Robert (1983). "Balanced Trees". Algorithms. Addison-Wesley. p. 199. ISBN 0-201-06672-6.
^ Adelson-Velsky, Georgy; Landis, Evgenii (1962). "An algorithm for the organization of information". Proceedings of the USSR Academy of Sciences (in Russian). 146: 263–266. Myron J. Ricci의 소련 수학 번역 - Doklady, 3:1259–1263, 1962.
^ ^a ^b Pfaff, Ben (June 2004). "Performance Analysis of BSTs in System Software" (PDF). Stanford University.
^ AVL 트리는 무게 균형이 맞지 않습니까?(즉, AVL 트리는 μ밸런스가 되지 않습니다)
그 때문에, 다음과 같이 됩니다.바이너리 트리는 $\mu$ $0\leq \mu \leq {\tfrac {1}{2}}$ {\ $display$ style $\mu$ $0\leq \mu \leq {\tfrac {1}{2}}$ } - balanced $\mu$ 라고 $\mu$ , 0 $0\leq \mu \leq {\tfrac {1}{2}}$ 1 $0\leq \mu \leq {\tfrac {1}{2}}$ 2 \ $display style 0 \ leq$ \ leq { $tfrac {1}$ {2 $0\leq \mu \leq {\tfrac {1}{2}}$ 은(는) $0\leq \mu \leq {\tfrac {1}{2}}$ $노드$ N {\ $displaystyle$ N $N$ 에 대해 부등식,
${1}{2}}-\mu \leq {\tfrac { N_{l} {N +1}}\leq {\tfrac {1}+\mu$
$\mu$ 속성에서는 μ $(\displaystyle\mu)$ 가 $\mu$ 최소입니다. $displaystyle$ N $)$ 은 $|N|$ 트리 아래의 노드 $,$ $($ $루트$ 포함)은 $N$ N(\ $displaystyle N_{l$ })은 $N_{l}$ N $(\displaystyle$ N $N$ 의 왼쪽 자식 노드입니다.
^ ^a ^b ^c ^d Knuth, Donald E. (2000). Sorting and searching (2. ed., 6. printing, newly updated and rev. ed.). Boston [u.a.]: Addison-Wesley. ISBN 0-201-89685-0.
^ Rajinikanth. "AVL Tree : Data Structures". btechsmartclass.com. Retrieved 2018-03-09.
^ 단, 잔액 정보는 부모보다 1이 높은지 2가 높은지를 나타내는 1비트로 자녀 노드에 유지할 수 있으므로 자녀 모두 2가 높은 것은 할 수 없다.AVL 트리는 Haupler, Sen 및 Tarjan이 만든 "순위 균형" 나무입니다.
^ Dixit, J. B. (2010). Mastering data structures through 'C' language. New Delhi, India: University Science Press, an imprint of Laxmi Publications Pvt. Ltd. ISBN 9789380386720. OCLC 939446542.
^ ^a ^b ^c Brass, Peter (2008). Advanced data structures. Cambridge: Cambridge University Press. ISBN 9780511438202. OCLC 312435417.
^ Hubbard, John Rast (2000). Schaum's outline of theory and problems of data structures with Java. New York: McGraw-Hill. ISBN 0071378707. OCLC 48139308.
^ ^a ^b ^c Pfaff, Ben (2004). An Introduction to Binary Search Trees and Balanced Trees. Free Software Foundation, Inc.
^ Weiss, Mark Allen. (2006). Data structures and algorithm analysis in C++ (3rd ed.). Boston: Pearson Addison-Wesley. p. 145. ISBN 0-321-37531-9. OCLC 61278554.{{cite book}}: CS1 유지보수: 날짜 및 연도(링크)
^ ^a ^b 를 클릭합니다Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2016), "Just join for parallel ordered sets", Symposium on Parallel Algorithms and Architectures, ACM, pp. 253–264, arXiv:1602.02120, doi:10.1145/2935764.2935768, ISBN 978-1-4503-4210-0, S2CID 2897793.
^ Paul E. Black (2015-04-13). "AVL tree". Dictionary of Algorithms and Data Structures. National Institute of Standards and Technology. Retrieved 2016-07-02.
^ Kurt Melhorn, Peter Sanders: "알고리즘과 데이터 구조.기본 툴박스"Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77977-3, doi:10.1007/978-3-540-77978-0.
^ Dinesh P.Mehta, Sartaj Sahni (Ed.) 데이터 구조 및 애플리케이션 핸드북 10.4.2
^ 적색-검은색 트리#점근 경계 증명

추가 정보

도널드 크누트.The Art of Computer Programming, 제3권: Sorting and Searching, 제3판.애디슨 웨슬리, 1997년ISBN 0-201-89685-0.섹션 6.2.3의 458~475 페이지: 균형 나무.
를 클릭합니다Haeupler, Bernhard; Sen, Siddhartha; Tarjan, Robert E. (2015), "Rank-balanced trees" (PDF), ACM Transactions on Algorithms, 11 (4): Art. 30, 26, doi:10.1145/2689412, MR 3361215, S2CID 1407290.

외부 링크

이 문서에는 NIST 문서의 퍼블릭 도메인 자료가 포함되어 있습니다.

[wiscurl-1] ^ ^a ^b ^c ^d ^e ^f Eric Alexander. "AVL Trees". Archived from the original on July 31, 2019.{{cite web}}: CS1 유지보수: 부적합한 URL(링크)

[2] Sedgewick, Robert (1983). "Balanced Trees". Algorithms. Addison-Wesley. p. 199. ISBN 0-201-06672-6.

[3] Adelson-Velsky, Georgy; Landis, Evgenii (1962). "An algorithm for the organization of information". Proceedings of the USSR Academy of Sciences (in Russian). 146: 263–266. Myron J. Ricci의 소련 수학 번역 - Doklady, 3:1259–1263, 1962.

[Pfaff1-4] Pfaff, Ben (June 2004). "Performance Analysis of BSTs in System Software" (PDF). Stanford University.

[5] AVL 트리는 무게 균형이 맞지 않습니까?(즉, AVL 트리는 μ밸런스가 되지 않습니다)
그 때문에, 다음과 같이 됩니다.바이너리 트리는 $\mu$ $0\leq \mu \leq {\tfrac {1}{2}}$ {\ $display$ style $\mu$ $0\leq \mu \leq {\tfrac {1}{2}}$ } - balanced $\mu$ 라고 $\mu$ , 0 $0\leq \mu \leq {\tfrac {1}{2}}$ 1 $0\leq \mu \leq {\tfrac {1}{2}}$ 2 \ $display style 0 \ leq$ \ leq { $tfrac {1}$ {2 $0\leq \mu \leq {\tfrac {1}{2}}$ 은(는) $0\leq \mu \leq {\tfrac {1}{2}}$ $노드$ N {\ $displaystyle$ N $N$ 에 대해 부등식,
${1}{2}}-\mu \leq {\tfrac { N_{l} {N +1}}\leq {\tfrac {1}+\mu$
$\mu$ 속성에서는 μ $(\displaystyle\mu)$ 가 $\mu$ 최소입니다. $displaystyle$ N $)$ 은 $|N|$ 트리 아래의 노드 $,$ $($ $루트$ 포함)은 $N$ N(\ $displaystyle N_{l$ })은 $N_{l}$ N $(\displaystyle$ N $N$ 의 왼쪽 자식 노드입니다.

[Knuth-6] Knuth, Donald E. (2000). Sorting and searching (2. ed., 6. printing, newly updated and rev. ed.). Boston [u.a.]: Addison-Wesley. ISBN 0-201-89685-0.

[7] Rajinikanth. "AVL Tree : Data Structures". btechsmartclass.com. Retrieved 2018-03-09.

[8] 단, 잔액 정보는 부모보다 1이 높은지 2가 높은지를 나타내는 1비트로 자녀 노드에 유지할 수 있으므로 자녀 모두 2가 높은 것은 할 수 없다.AVL 트리는 Haupler, Sen 및 Tarjan이 만든 "순위 균형" 나무입니다.

[dixit-mastering-data-structures-9] Dixit, J. B. (2010). Mastering data structures through 'C' language. New Delhi, India: University Science Press, an imprint of Laxmi Publications Pvt. Ltd. ISBN 9789380386720. OCLC 939446542.

[brass-advanced-data-structures-10] Brass, Peter (2008). Advanced data structures. Cambridge: Cambridge University Press. ISBN 9780511438202. OCLC 312435417.

[hubbard-outline-theory-problems-11] Hubbard, John Rast (2000). Schaum's outline of theory and problems of data structures with Java. New York: McGraw-Hill. ISBN 0071378707. OCLC 48139308.

[Pfaff-12] Pfaff, Ben (2004). An Introduction to Binary Search Trees and Balanced Trees. Free Software Foundation, Inc.

[13] Weiss, Mark Allen. (2006). Data structures and algorithm analysis in C++ (3rd ed.). Boston: Pearson Addison-Wesley. p. 145. ISBN 0-321-37531-9. OCLC 61278554.{{cite book}}: CS1 유지보수: 날짜 및 연도(링크)

[join-based-14] 를 클릭합니다Blelloch, Guy E.; Ferizovic, Daniel; Sun, Yihan (2016), "Just join for parallel ordered sets", Symposium on Parallel Algorithms and Architectures, ACM, pp. 253–264, arXiv:1602.02120, doi:10.1145/2935764.2935768, ISBN 978-1-4503-4210-0, S2CID 2897793.

[15] Paul E. Black (2015-04-13). "AVL tree". Dictionary of Algorithms and Data Structures. National Institute of Standards and Technology. Retrieved 2016-07-02.

[16] Kurt Melhorn, Peter Sanders: "알고리즘과 데이터 구조.기본 툴박스"Springer, Berlin/Heidelberg 2008, ISBN 978-3-540-77977-3, doi:10.1007/978-3-540-77978-0.

[Dinesh-17] Dinesh P.Mehta, Sartaj Sahni (Ed.) 데이터 구조 및 애플리케이션 핸드북 10.4.2

[18] 적색-검은색 트리#점근 경계 증명

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[18]

v t 트리 데이터 구조
트리 검색 (다이나믹 세트/어소시에이션 어레이)	2–3 2–3–4 AA (a, b) AVL B B+ B* B^x. (최적) 바이너리 검색 춤추다 HTree 간격 주문통계 (좌향) 레드-블랙 희생양 스플라이 T 나무 UB 무게 밸런스
수북이	바이너리 이항 브로달 피보나치 좌파 페어링 스큐 판 엠데 보아스 약한
시도하다	Ctrie C-trie(압축 ADT) 해시 기수 서픽스 삼진수 검색 X-Fast 고속
공간 데이터 파티션 트리	공 BK BSP 데카르트어 힐베르트 R k-d(표준 k-d) M 미터법 MVP 옥트리 PH 우선 순위 R 쿼드 R R+ R* 부분 부사장 X
기타 트리	덮다 지수 펜윅 손가락. 프랙탈 트리 인덱스 퓨전 해시 캘린더 i디스턴스 K-ary 좌측자녀 우측자매 링크/컷 로그 구조화 결합 머클 p q. 범위 SPQR 정상

v t 잘 알려진 데이터 구조
종류들	수집 컨테이너.
추상적인	연관 배열 멀티맵 데이터 구조 검색 목록. 스택 큐 더블 엔드 큐 priority 큐 이중 엔드 priority 큐 세트 멀티셋 디조인트 세트
어레이	비트 배열 순환 버퍼 다이내믹 어레이 해시 테이블 해시 어레이 트리 희박 행렬
링크되어 있다	어소시에이션리스트 링크 리스트 스킵 리스트 언롤링된 링크 리스트 XOR 링크 리스트
나무들	B-트리 이진 검색 트리 AA나무 AVL 트리 붉은색-검은색 셀프밸런싱 트리 스플레이 트리 히프 이진 힙 이항 힙 피보나치 힙 R 트리 R* 트리 R+ 트리 힐베르트 R-트리 트리 해시 트리
그래프	이항 결정도 방향 비순환 그래프 지시 비순환 단어 그래프
데이터 구조 목록

Search

AVL 트리

네임스페이스

더

목차

정의.

밸런스 팩터

특성.

운용

검색 중

트래버설

삽입

삭제

작업 및 대량 작업 설정

재조정

심플 로테이션

이중 회전

다른 구조물과의 비교

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

AVL 트리

정의.

밸런스 팩터

특성.

운용

검색 중

트래버설

삽입

삭제

작업 및 대량 작업 설정

재조정

심플 로테이션

이중 회전

다른 구조물과의 비교

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.