분리 집합 데이터 구조

Disconnect-set/Union-find 포레스트
Disconnect-set/Union-find 포레스트
유형	멀티웨이 트리
발명된	1964
발명자	버나드 A 갤러와 마이클 J. 피셔
빅 O 표기의 시간 복잡도
알고리즘.
알고리즘.
공간
서치
머지

MakeSet는 8싱글톤을 만듭니다.

일부 조작 후Union일부 세트는 함께 그룹화되어 있습니다.

컴퓨터 과학에서, Union-find 데이터 구조 또는 merge-find 집합이라고도 하는, 분리된(중복되지 않는) 집합의 집합을 저장하는 데이터 구조입니다.마찬가지로 집합의 파티션을 분리된 부분 집합으로 저장합니다.새 집합을 추가하고 집합을 병합(결합으로 대체)하고 집합의 대표 멤버를 찾기 위한 작업을 제공합니다.마지막 연산을 통해 두 요소가 같은 세트 또는 다른 세트에 있는지 효율적으로 확인할 수 있습니다.

분리 집합 데이터 구조를 구현하는 방법은 여러 가지가 있지만, 실제로는 분리 집합 포레스트라고 불리는 특정 구현으로 식별되는 경우가 많습니다.이것은 거의 일정한 상각시간 내에 결합을 수행하고 찾는 특수한 유형의 숲입니다.n개의 노드가 $있는$ 분리된 집합 포레스트에서 m의 덧셈, 결합 또는 찾기 $작업$ 을 수행하려면 총 $시간$ O $(mα (n)$ 가 필요합니다. $여기서$ α( $n)$ 는 극도로 느리게 성장하는 역 Ackermann 함수입니다.분리 집합 포리스트는 작업별로 이 성능을 보장하지 않습니다.개별 합집합 및 찾기 작업은 $일정$ 시간α $(n$ ) 시간보다 오래 걸릴 수 있지만, 각 연산에 따라 연속된 연산이 더 빨리 이루어지도록 분리된 포리스트가 스스로 조정됩니다.분리된 집합 포레스트는 점근적으로 최적이며 실질적으로 효율적이다.

분리 집합 데이터 구조는 그래프의 최소 스패닝 트리를 찾는 Kruskal 알고리즘에서 중요한 역할을 합니다.최소 스패닝 트리의 중요성은 다양한 알고리즘의 기초가 되는 분리 집합 데이터 구조임을 의미합니다.또한, 분리된 데이터 구조는 특히 레지스터 할당 문제에 대한 컴파일러에서도 마찬가지로 심볼 계산에도 적용된다.

역사

분리 집합 포레스트는 Bernard A에 의해 처음 설명되었습니다. 갤러와 마이클 J. 1964년 ^[2]피셔.1973년 홉크로프트와 울먼에 ^[3]의해 시간 복잡도는 O $log$ $O(\log ^{*}(n))$ n ( $O(\log ^{*}(n))$ ) { $displaystyle$ O $(\$ $log$ $^{*}(n$ $n$ 로 제한되었다 $.$ 1975년 Robert Tarjan은 알고리즘의 시간 ^[4]복잡도에 대한 O $O(m\alpha (n))$ α ( $O(m\alpha (n))$ ) $){displaystyle$ O $(m\alpha (n)}}($ 역 애커만 함수) 상한을 $O(m\alpha (n))$ 로 증명했으며 1979년에는 이것이 제한된 경우의 ^[5]하한임을 보여주었다.1989년 Fredman과 Saks는 ^[6] $\Omega (\alpha (n))$ ( $\Omega (\alpha (n))$ ) { $displaystyle \Omega (\alpha (n)}}$ $\Omega (\alpha (n))$ (암모르티드) 단어가 연산별로 분리된 데이터 구조에서 접근해야 한다는 것을 보여 데이터 구조의 최적성을 입증했다.

1991년 갈릴과 이탈리아노는 분리 ^[7]집합의 데이터 구조에 대한 조사를 발표했다.

1994년 Richard J. Anderson과 Heather Woll은 ^[8]차단할 필요가 없는 Union-Find의 병렬화 버전을 설명했습니다.

2007년 Sylvain Conchon과 Jean-Christophe Filliattre는 분리된 포레스트 데이터 구조의 반영구 버전을 개발하고 증명 보조 Coq를 사용하여 ^[9]그 정확성을 공식화했다."Semi-persistent"는 구조의 이전 버전이 효율적으로 유지되지만 데이터 구조의 이전 버전에 액세스하면 이후 버전이 무효화됨을 의미합니다.가장 빠른 구현으로 비영구적 알고리즘과 거의 같은 성능을 달성할 수 있습니다.이들은 복잡도 분석을 수행하지 않습니다.

표현

분리 집합 포레스트의 각 노드는 포인터와 크기 또는 순위(둘 다 아님) 중 하나의 보조 정보로 구성됩니다.포인터는 트리의 루트가 아닌 각 노드가 부모를 가리키는 부모 포인터 트리를 만드는 데 사용됩니다.루트 노드를 다른 노드와 구별하기 위해 부모 포인터에는 노드에 대한 순환 참조나 Sentinel 값과 같은 잘못된 값이 있습니다.각 트리는 포리스트에 저장된 집합을 나타내며 집합의 구성원은 트리의 노드가 됩니다.루트 노드는 세트 대표자를 제공합니다.노드를 포함하는 트리의 루트가 동일한 경우에만 두 노드가 동일한 집합에 있습니다.

포레스트 내의 노드는 애플리케이션에 편리한 방법으로 저장할 수 있지만 일반적인 방법은 어레이에 저장하는 것입니다.이 경우 상위 항목은 배열 인덱스로 나타낼 수 있습니다.각 어레이 엔트리는 부모 포인터용으로 $δ(log$ n $)$ 비트의 스토리지를 필요로 합니다.엔트리의 나머지 부분에는 동등 이하의 스토리지가 필요하기 때문에 포레스트를 저장하는 데 필요한 비트 수는 $δ(n$ $log$ n $)$ 입니다.구현에서 고정 크기 노드를 사용하는 경우(따라서 저장할 수 있는 포리스트의 최대 크기를 제한함), 필요한 스토리지는 n $단위$ 로 선형입니다.

운용

분리 집합 데이터 구조는 새 요소를 포함하는 새 집합 만들기, 지정된 요소를 포함하는 집합의 대표 찾기 및 두 집합 병합의 세 가지 작업을 지원합니다.

새 세트 만들기

그MakeSetoperation은 새 요소만 포함하는 새 세트에 새 요소를 추가하고 새 세트가 데이터 구조에 추가됩니다.데이터 구조가 세트의 파티션으로 표시되는 경우,MakeSetoperation은 새 요소를 추가하여 세트를 확대하고 새 요소만 포함하는 새 하위 집합에 새 요소를 추가하여 기존 파티션을 확장합니다.

분리된 숲에서MakeSet는 노드의 부모 포인터와 노드의 크기 또는 순위를 초기화합니다.루트가 자신을 가리키는 노드에 의해 표현되는 경우 요소 추가는 다음 의사코드를 사용하여 설명할 수 있습니다.

함수 MakeSet(x)는 x가 아직 포리스트에 없는 경우 x.parent := x.size := 1 // 노드가 크기 x.rank := 0 //가 저장되는 경우 노드가 순위 끝을 저장하는 경우(함수가 종료되는 경우)입니다.

이 작업은 항상 시간이 복잡합니다.특히 노드 n개로 $분리$ 된 집합 포리스트를 초기화하려면 O $(n)$ 시간이 $필요$ 합니다.

실제로,MakeSet $메모리$ 할당이 적절한 동적 배열 구현과 마찬가지로 상각된 상수 시간 작업인 한 랜덤 집합 포리스트의 점근적 성능은 변경되지 않습니다.

정해진 대표자를 찾는 중

그Find작업은 루트 요소에 $도달$ 할 때까지 지정된 쿼리 노드x로부터의 부모 포인터의 체인을 따릅니다.이 루트 요소는 x가 $속한$ 집합을 나타내며 x $자체$ 일 수 있습니다. Find도달하는 루트 요소를 반환합니다.

의 실행Find운영은 숲을 개선할 수 있는 중요한 기회를 제공한다.의 시간Find조작은 부모 포인터를 쫓는데 소비되기 때문에 트리가 평평할수록 빨라집니다.Find운용을 실시합니다.어떤 경우Find루트에 도달하려면 각 부모 포인터를 연속해서 따라가야 합니다.그러나 이 검색 중에 방문한 상위 포인터는 루트에 더 가까운 지점을 가리키도록 업데이트할 수 있습니다.루트로 가는 길에 방문한 모든 요소는 동일한 세트의 일부이므로 포리스트에 저장된 세트는 변경되지 않습니다.하지만 그것은 미래를 만든다.Find쿼리 노드와 루트 사이의 노드뿐만 아니라 그 하위 노드도 보다 빠르게 작업을 수행할 수 있습니다.이 업데이트는 분할 집합 포리스트의 상각된 성능 보증의 중요한 부분입니다.

에는 몇 가지 알고리즘이 있습니다.Find점근적으로 최적의 시간 복잡성을 달성합니다.경로 압축이라고 하는 알고리즘 패밀리는 쿼리 노드와 루트 포인트 사이의 모든 노드를 루트로 만듭니다.경로 압축은 다음과 같이 단순한 재귀를 사용하여 구현할 수 있습니다.

함수 Find(x)는 x.parent x x이면 x.parent : = Find(x.parent) return x.parent 그렇지 않으면 끝 함수의 경우 x end를 반환합니다.

이 실장에서는 2개의 패스(트리의 위쪽과 아래쪽)가 이루어집니다.쿼리 노드에서 루트로의 패스를 저장하기 위해서는 충분한 스크래치메모리가 필요합니다(위의 의사코드에서는 패스는 콜스택을 사용하여 암묵적으로 표현됩니다).이것은, 양쪽의 패스를 같은 방향으로 실행함으로써, 일정량의 메모리로 저감 할 수 있습니다.상시 메모리 구현은 루트를 찾기 위해, 포인터를 업데이트하기 위해 쿼리 노드에서 루트로 두 번 이동합니다.

찾기(x) 함수는 루트 := x인 반면 루트.부모 root 루트가 루트 := root.부모 끝인 반면 x.parent root 루트가 부모 := x.parent x.parent := 루트 x := 부모 끝인 반면 루트 끝 함수는 반환됩니다.

Tarjan과 Van Leeuwen도 원패스를 개발했다.Find알고리즘은 최악의 경우 복잡성은 그대로 ^[4]유지하지만 실제로는 더 효율적입니다.이를 패스 분할 및 패스 하프링이라고 합니다.둘 다 쿼리 노드와 루트 사이의 경로에 있는 노드의 부모 포인터를 업데이트합니다.경로 분할은 해당 경로의 모든 상위 포인터를 노드의 조부모에 대한 포인터로 대체합니다.

함수 찾기(x)는 x.parent x x do (x, x.parent) := (x.parent, x.parent.parent)가 종료되는 동안 x end 함수를 반환합니다.

경로 분할은 비슷하게 작동하지만 다른 모든 부모 포인터만 대체합니다.

함수 찾기(x)는 x.parent x x do x.parent := x.parent x := x.parent x := x.parent end인 동안 x.parent end 함수가 반환됩니다.

두 세트의 병합

조작Union(x, y)는 x를 $포함$ 하는 세트와 y를 $포함$ 하는 세트를 합계로 바꿉니다. Union최초 사용Find $x$ 와 y를 $포함$ 하는 나무의 뿌리를 결정합니다.뿌리가 같으면 더 이상 할 일이 없다.그렇지 않으면 두 트리를 병합해야 합니다.이것은 x 루트의 $부모$ 포인터를 $y$ 로 설정하거나 y 루트의 $부모$ 포인터를 $x$ 로 설정함으로써 이루어집니다.

어느 노드를 부모로 할지에 따라 트리의 향후 운용이 복잡해집니다.부주의하게 하면 나무가 지나치게 커질 수 있다.예를 들어 다음과 같이 가정합니다.Union항상 x를 $포함$ 하는 트리를 y를 $포함$ 하는 트리의 하위 트리로 만듭니다. $1,2,3,\ldots ,n,$ 1, $1,2,3,\ldots ,n,$ , $1,2,3,\ldots ,n,$ , $1,2,3,\ldots ,n,$ n $,$ {\ $displaystyle$ 1, $2$ , 3 $,$ $\ldots, n,}$ 으로 $1,2,3,\ldots ,n,$ 초기화된 포레스트에서 시작하여 실행합니다. $Union(1, 2)$ , $Union(2, 3)$ , ..., $Union(n - 1, n)$ . 결과 포레스트에는 $루트$ 가 n인 단일 트리가 포함되어 있으며, $1에서n$ 까지의 경로는 트리의 모든 노드를 통과합니다.이 포레스트의 경우 실행 시간은Find(1)O $(n)$ 입니다.

효율적인 구현에서는 크기별 결합 또는 등급별 결합을 사용하여 나무 높이를 제어한다.둘 다 부모 포인터 외에 노드도 정보를 저장해야 합니다.이 정보는 어떤 루트가 새 부모가 될지를 결정하는 데 사용됩니다.두 가지 전략 모두 나무가 너무 깊어지지 않도록 합니다.

크기별로 합칠 경우 노드에는 크기가 저장됩니다.이것은 단순히 하위 노드(노드 자체 포함)의 개수입니다. $루트$ $x$ 와 y를 가진 트리가 병합되면 하위 노드가 더 많은 상위 노드가 됩니다.두 노드의 하위 노드 수가 같을 경우 어느 한쪽이 부모가 될 수 있습니다.두 경우 모두 새 상위 노드의 크기는 새 하위 노드 총 개수로 설정됩니다.

function Union(x, y) is // Replace nodes by roots x := Find(x)     y := Find(y)      if x = y then return // x and y are already in the same set end if // If necessary, rename variables to ensure that // x has at least as many descendants as y if x.size < y.size then         (x, y) := (y, x)     end if // Make x the new root y.parent := x // Upd먹었다. x.size 크기 : = x.size + y.size 끝 함수

크기를 저장하기 위해 필요한 비트 수는 n을 $저장$ 하기 위해 필요한 비트 수입니다.따라서 포리스트에 필요한 스토리지에 일정한 요소가 추가됩니다.

순위별 결합의 경우 노드는 해당 높이의 상한인 순위를 저장합니다.노드가 초기화되면 그 순위는 0으로 설정됩니다. $루트$ $x$ 와 y를 사용하여 트리를 병합하려면 먼저 트리의 순위를 비교합니다.순위가 다르면 큰 순위 트리가 부모가 되고 $x$ 와 $y$ 의 순위는 변경되지 않습니다.순위가 같을 경우 어느 한쪽이 부모가 될 수 있지만 새 부모의 순위는 1씩 증가합니다.노드의 순위는 높이와 관련이 있지만, 높이를 저장하는 것보다 순위를 저장하는 것이 더 효율적입니다.노드 높이는 다음 중 변경될 수 있습니다.Find따라서 순위를 저장하면 높이를 올바르게 유지하는 추가적인 노력이 필요하지 않습니다.의사 코드에서 등급별 결합은 다음과 같습니다.

뿌리 x에 의해 기능 Union(), y)은// 바꾸기 노드::Find(y)만약 x)y 그러면을 끓여= Find())는 y= cm이고 만약 끓여만약 필요한 이름을 변수가 끓여)적어도 그는 y의 마치x.rank<> 큰 rank을 갖도록 하는 어두워져서 이미 같은 세트 끝에 있다;y.rank 다음(), y):)(y는 x)끝 만약 //) 새로운 뿌리 y.parent 활용하라:=-1을 끓여나fneccessary, x.rank = y.rank이면 x의 순위를 증가시키고 x.rank : = x.rank + end function이면 1개의 끝

모든 노드에 랭크 $\lfloor \log n\rfloor$ 「log $\lfloor \log n\rfloor$ $「\displaystyle \lfloor \log$ n $\rfloor$ }이하의 $\lfloor \log n\rfloor$ ^[10]것이 표시됩니다.따라서 순위를 O $(log$ $log$ n $)$ 비트로 저장할 수 $있으므로$ 포레스트 크기의 점근적으로 무시할 수 있는 부분이 된다.

위의 실장에서는 노드가 트리의 루트가 아닌 한 노드의 크기와 순위는 중요하지 않다는 것이 명백합니다.노드가 자노드가 되면 노드의 크기와 등급은 다시 액세스되지 않습니다.

시간의 복잡성

포레스트의 디커넥션 세트 실장에서는Find부모 포인터는 갱신되지 않습니다.Union는 트리 높이를 제어하려고 하지 않으며 높이가 O $(n)$ 인 트리를 가질 수 있습니다.이런 상황에서Find그리고.Union $조작$ 에는 O(n $)$ $시간$ 이 필요합니다.

구현에서 경로 압축만 사용하는 경우 n개의 $시퀀스는$ MakeSet $동작$ 에 이어 $최대$ n - 1의 동작 Union $조작$ 과 f Findoperations는 최악의 경우 실행시간이 $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$ ( $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$ + $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$ $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$ ( $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$ + $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$ 2 + $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$ / $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$ n $){$ $display$ style \ $Theta ( n$ + $f$ \ $cdot \$ left ( $1$ + \ $log$ _ { $2$ + $f$ / $n } n$ \ $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$ right ) $\Theta (n+f\cdot \left(1+\log _{2+f/n}n\right))$ ^[10]。

순위별 결합을 사용하지만 상위 포인터를 업데이트하지 않음Find는 임의의 유형의 m개 동작에 대해 $실행시간$ 을 $\Theta (m\log n)$ log $\Theta (m\log n)$ n $)(\displaystyle \Theta(m\log$ n $)}$ 으로 $\Theta (m\log n)$ 지정합니다.이 중 $최대$ n개의 동작은 다음과 같습니다.MakeSet운용을 실시합니다.^[10]

패스 압축, 분할 또는 절반의 조합과 크기별 또는 랭크별 결합을 조합하면 모든 유형의 m개 동작의 $실행$ 시간이 단축됩니다.이 중 $최대$ n개는 다음과 같습니다.MakeSet $\Theta (m\alpha (n))$ $\Theta (m\alpha (n))$ $\Theta (m\alpha (n))$ α $\Theta (m\alpha (n))$ ( $\Theta (m\alpha (n))$ ) $\Theta (m\alpha (n))$ \ $displaystyle$ \ $Theta ( m$ \ $alpha$ ( $n$ ) $\Theta (m\alpha (n))$ ^[4]^[5]。이것에 의해, 각 동작의 상각 실행 시간이 $\Theta (\alpha (n))$ ( $\Theta (\alpha (n))$ $){displaystyle \Theta$ (\ $alpha (n)}$ 가 됩니다 $\Theta (\alpha (n))$ 이것은 점근적으로 최적입니다.즉, 모든 분리 집합 데이터 구조는 $\Omega (\alpha (n))$ ^[6] $\Omega (\alpha (n))$ (α $\Omega (\alpha (n))$ ( $\Omega (\alpha (n))$ $){displaystyle \Omega (\alpha (n$ )}}}의 $\Omega (\alpha (n))$ 상각 시간을 사용해야 합니다. $\alpha (n)$ 서 함수 $\alpha (n)$ ( n ) $\alpha (n)$ \ $style \alpha ($ n )는 $\alpha (n)$ 역 Ackermann 함수입니다.역아커만 함수는 놀라울 정도로 느리게 성장하기 때문에 실제로 물리적 우주에 쓸 수 있는 $n개$ 의 경우 이 인수는 4 $이하$ 입니다.따라서 분할 집합 연산은 실질적으로 상각된 상수 시간이 됩니다.

Union-Find의 O(m log*n) 시간 복잡성 증명

분리된 숲의 성능에 대한 정확한 분석은 다소 복잡하다.그러나, $m$ 에 대한 상각 시간이 더 간단하다는 것을 증명하는 분석이 있다. Find또는Unionn개의 객체를 $포함$ 하는 분할 집합 포레스트에서의 연산은 O $(mlog *$ n $)$ 입니다. $여기$ 서^* log는 반복 ^[11]^[12]^[13]^[14]로그를 나타냅니다.

Lemma 1: 찾기 함수가 루트를 따라 경로를 따라 이동함에 따라 발견된 노드의 순위가 증가합니다.

증명

데이터 세트에 Find 및 Union 연산이 적용되므로 이 사실은 시간이 지남에 따라 계속 유효하다고 주장합니다.처음에는 각 노드가 자체 트리의 루트일 때 거의 맞습니다.노드의 순위가 변경될 수 있는 유일한 경우는 Union by Rank 연산이 적용되는 경우입니다.이 경우 순위가 낮은 트리는 순위가 높은 트리에 부착되며, 순위가 낮은 트리는 순위가 높은 트리에 부착됩니다.그리고 찾기 작업 중에 경로를 따라 방문한 모든 노드가 자식보다 순위가 큰 루트에 연결되므로 이 작업도 이 사실을 변경하지 않습니다.

Lemma 2: $랭크$ r의 서브트리의 루트인 $노드$ u는 $2^{r}$ $2^{r}$ 의 r $(\$ 2 $^{r})$ 노드를 $2^{r}$ 가진다.

증명

처음에는 각 노드가 자체 트리의 루트일 때 거의 맞습니다. $랭크$ 가 $r$ 인 노드u에 $적어도2개$ 의^r 노드가 있다고 가정합니다.그런 다음 $등급별$ 유니언(Union by Rank) 연산을 사용하여 순위가 $r$ + $1인$ 트리가 병합되면, 루트가 $2^{r}+2^{r}=2^{r+1}$ 2 $2^{r}+2^{r}=2^{r+1}$ + $2^{r}+2^{r}=2^{r+1}$ $2^{r}+2^{r}=2^{r+1}$ $2^{r}+2^{r}=2^{r+1}$ r + $2^{r}+2^{r}=2^{r+1}$ ${\$ 2 $^{r}$ + $2^{r$ } = $2^{r+1}}$ 개의 $2^{r}+2^{r}=2^{r+1}$ 노드를 갖는 결과가 된다.

$Lemma$ 3: r랭크의 ${\frac {n}{2^{r}}}.$ 노드 수는 ${\frac {n}{2^{r}}}.$ ${\frac {n}{2^{r}}}.$ r $.$ ${{displaystyle {n}{2^{$ }}}입니다. $}$

증명

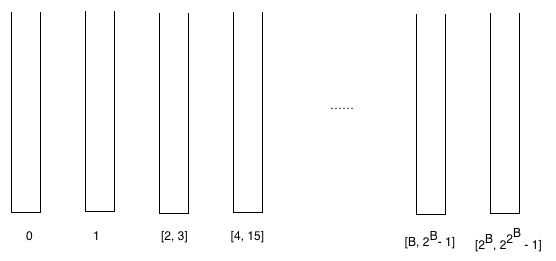
lema 2에서 $랭크$ 가 r인 서브트리의 루트인 $노드$ u에는 $2^{r}$ $2^{r}$ 의 r $(\$ 2 $^{r})$ 노드가 $2^{r}$ 있음을 알 수 있습니다. $랭크$ 가 r인 각 노드가 $2^{r}$ $2^{r}$ 의 r $(\$ }) 노드를 가진 트리의 루트인 경우 $랭크$ 가 r인 노드의 최대 수를 가져옵니다.이 경우 $랭크$ r의 노드 수는 ${\frac {n}{2^{r}}}.$ ${\frac {n}{2^{r}}}.$ r 입니다 $.{$ $displaystyle$ \ $frac$ { $n$ } { 2 ${\frac {n}{2^{r}}}.$ ^ { $r$ } 。 $}$

편의상 "버킷"을 정의합니다. 버킷은 특정 순위를 가진 정점을 포함하는 집합입니다.

몇 개의 버킷을 작성하고 그 랭킹에 따라 꼭지점을 버킷에 넣습니다.즉, 순위가 0인 정점은 0번째 버킷에 들어가고, 순위가 1인 정점은 첫 번째 버킷에 들어가고, 순위가 2와 3인 정점은 두 번째 버킷에 들어갑니다.B번째 버킷에 간격 $\left[r,2^{r}-1\right]=[r,R-1]$ [ $\left[r,2^{r}-1\right]=[r,R-1]$ $\left[r,2^{r}-1\right]=[r,R-1]$ r - $\left[r,2^{r}-1\right]=[r,R-1]$ $\left[r,2^{r}-1\right]=[r,R-1]$ [ $\left[r,2^{r}-1\right]=[r,R-1]$ , $\left[r,2^{r}-1\right]=[r,R-1]$ - $]$ = [ r , $2^$ { $r }$ - $1$ \ $right$ ]= [ $r$ , R - $\left[R,2^{R}-1\right].$ $\left[r,2^{r}-1\right]=[r,R-1]$ ][ B + 1)번째 $\left[r,2^{r}-1\right]=[r,R-1]$ 버킷에는 간격 $\left[R,2^{R}-1\right].$ $\left[R,2^{R}-1\right].$ $2$ - 1 $\left[R,2^{R}-1\right].$ 의 순위가 매겨진 정점이 포함됩니다 $.{$ 2 $}$ \ $style$ $}$

Proof

O(\log ^{*}n)

O (

O(\log ^{*}n)

O(\log ^{*}n)

) {

displaystyle

O ( \

log

^ { * n

O(\log ^{*}n)

) } Union

O(\log ^{*}n)

Find

버킷에 대해 두 가지 관찰을 할 수 있습니다.

총 버킷 수는 최대 $logn$ 입니다^*.
증명: 1개의 버킷에서 다음 버킷으로 이동할 때 1개의 2를 더합니다.즉, [ $\left[B,2^{B}-1\right]$ $\left[B,2^{B}-1\right]$ - $]({$ $left$ $\left[B,2^{B}-1\right]$ [ $B$ $, 2^{B}-1\right$ 에 $\left[B,2^{B}-1\right]$ 대한 다음 버킷은 [ $,$ - 1 $]({2^{B$ }, 2 $^{$ 2-right $})$ 가 됩니다.
버킷 $\left[B,2^{B}-1\right]$ [ $\left[B,2^{B}-1\right]$ $\left[B,2^{B}-1\right]$ B - $]{$ 의 $\left[B,2^{B}-1\right]$ 최대 요소 수는 ${\frac {2n}{2^{B}}}$ $({displaystyle$ { $2n}{$ 2^{ $B}}}})$ 입니다.
증명: 버킷 $\left[B,2^{B}-1\right]$ [ $\left[B,2^{B}-1\right]$ $\left[B,2^{B}-1\right]$ - $]({$ 의 $\left[B,2^{B}-1\right]$ 최대 요소 수는 ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$ ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$ B + ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$ B + ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$ + ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$ B + ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$ ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$ + ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$ - 1 ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$ 2 ${\frac {n}{2^{B}}}+{\frac {n}{2^{B+1}}}+{\frac {n}{2^{B+2}}}+\cdots +{\frac {n}{2^{2^{B}-1}}}\leq {\frac {2n}{2^{B}}}.$ B 입니다 $.{$ $display$ style { $frac$ + 2 $} {$ } $\leq({frac {2n}{2^{B}}})$ $}$

$F$ 는 실행된 "검색" 작업 목록을 나타내며,

T_{1}=\sum _{F}{\text{(루트 링크)}}

\displaystyle T_{2}=\sum _{F}{\text{(버킷이 다른 곳을 통과하는 링크의 수)}}}

T_{3}=\sum _{F}{\text{(버킷이 같은 곳을 통과하는 링크의 수).}}

m개의 검색의 $총$ 비용은 $T=T_{1}+T_{2}+T_{3}.$ $T=T_{1}+T_{2}+T_{3}.$ $T=T_{1}+T_{2}+T_{3}.$ $T=T_{1}+T_{2}+T_{3}.$ + $T=T_{1}+T_{2}+T_{3}.$ 2 + $T=T_{1}+T_{2}+T_{3}.$ 3 입니다 $.$ {{ $displaystyle$ T $=T_{1}+T_{2}+T_{3}.$ $}$

각 찾기 작업은 루트로 이어지는 트래버설을 정확히 1개 만들기 때문에 T = $O (m)$ 가 $됩니다 1$ .

또, 상기 버킷수의 바운드로부터, $T =O *$ (mlogn $)$ 가₂ 됩니다.

T의 $경우 3$ $u$ 에서 $v$ 로 가장자리를 통과한다고 가정합니다. $여기$ 서 $u$ 와 v는 버킷 [B $, 2 B$ - $1]$ 에 랭크가 $있고$ v는 루트가 아닙니다(이러한 통과 시점에서는 통과가 $T$ 에서₁ 고려됩니다). $v_{1},v_{2},\ldots ,v_{k}$ 를 수정하고 $v_{1},v_{2},\ldots ,v_{k}$ $v_{1},v_{2},\ldots ,v_{k}$ , $v_{1},v_{2},\ldots ,v_{k}$ …, $vk$ (\ $displaystyle v_$ {1 $},$ v_{ $2},\ldots,$ v_ $v_{1},v_{2},\ldots ,v_{k}$ {k})의 $순서$ 를 $v_{1},v_{2},\ldots ,v_{k}$ 합니다.경로 압축으로 인해 루트에 대한 가장자리가 고려되지 않기 때문에 이 시퀀스에는 서로 다른 노드만 포함되며 Lemma 1 때문에 이 시퀀스의 노드 순위가 크게 상승하고 있음을 알 수 있습니다.양쪽 노드가 버킷에 있는 것으로 시퀀스 $길이$ k(노드 $u$ 가 같은 버킷 $내$ 의 다른 루트에 연결된 횟수)는 최대 2B $2^{B}-1-B<2^{B}.$ - $2^{B}-1-B<2^{B}.$ - $2^{B}-1-B<2^{B}.$ B < $2^{B}-1-B<2^{B}.$ . ${$ $display style$ 2 $^{B}-1-B$ < $2^{B})$ 라고 결론지을 수 있습니다. $}$

따라서 $T_{3}\leq \sum _{[B,2^{B}-1]}\sum _{u}2^{B}.$ [ $T_{3}\leq \sum _{[B,2^{B}-1]}\sum _{u}2^{B}.$ , $T_{3}\leq \sum _{[B,2^{B}-1]}\sum _{u}2^{B}.$ B - $T_{3}\leq \sum _{[B,2^{B}-1]}\sum _{u}2^{B}.$ ] 2 $T_{3}\leq \sum _{[B,2^{B}-1]}\sum _{u}2^{B}.$ 、 $T_{3}\leq \sum _{[B,2^{B}-1]}\sum _{u}2^{B}.$ 2 B $T_{3}\leq \sum _{[B,2^{B}-1]}\sum _{u}2^{B}.$ 。{ $display T_{3$ } \ $leq \sum _$ { [ B , $2$ ^ { $B$ } } \ $sum$ _ { $u$ } 2 ^ { $B$ } 。 $}$

관찰 1과 2에서 ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ 3 ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ 2 ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ 2 ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ log ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ 2 n $textstyle T_{3}\leq \sum$ _ ${B}2^{B$ }{\ $frac {2n}{2^{B}}}\leqn\log ^{$ n}이라고 ${\textstyle T_{3}\leq \sum _{B}2^{B}{\frac {2n}{2^{B}}}\leq 2n\log ^{*}n.}$ 을 내릴 수 있다. $}$

$T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ T $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ 1 $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ + $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ 2 + $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ ( $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ ∗ $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ ) n $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ ) . $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ { $displaystyle$ T= $T_{1$ } + $T_{2} = O$ ( $m$ \ $log$ ^ { * $T=T_{1}+T_{2}+T_{3}=O(m\log ^{*}n).$ } n ) 。 $}$

적용들

Kruskal 알고리즘을 사용하여 최소 스패닝트리를 찾을 때의 Union-Find 데모.

분리 집합 데이터 구조는 예를 들어 무방향 그래프의 연결된 구성 요소를 추적하기 위해 집합의 분할을 모델링합니다.그런 다음 이 모델을 사용하여 두 정점이 동일한 구성요소에 속하는지 또는 둘 사이에 모서리를 추가할 경우 주기가 발생하는지 여부를 확인할 수 있습니다.Union-Find 알고리즘은 ^[15]통합의 고성능 구현에 사용됩니다.

이 데이터 구조는 Boost Graph Library에서 증분 연결된 구성 요소 기능을 구현하는 데 사용됩니다.또한 그래프의 최소 스패닝 트리를 찾는 Kruskal 알고리즘을 구현하는 데 중요한 구성요소입니다.

분리 집합 포리스트로서의 정기적인 구현에서는 경로 압축이나 순위 경험적 접근법이 없는 경우에도 에지를 삭제할 수 없습니다.단, 일정시간 ^[16]삭제를 허용하는 최신 구현이 존재합니다.

Sharir와 Agarwal은 분리 집합의 최악의 거동과 컴퓨터 ^[17]기하학의 조합 구조인 데이븐포트-신젤 시퀀스의 길이 사이의 연관성을 보고한다.

「」를 참조해 주세요.

파티션 세분화: 분리된 세트를 유지하기 위한 다른 데이터 구조이며, 세트를 병합하지 않고 서로 분리하는 업데이트를 사용합니다.
동적 연결

레퍼런스

^ ^a ^b ^c ^d ^e ^f Tarjan, Robert Endre (1975). "Efficiency of a Good But Not Linear Set Union Algorithm". Journal of the ACM. 22 (2): 215–225. doi:10.1145/321879.321884. hdl:1813/5942. S2CID 11105749.
^ 분리된 포레스트를 발원지로 하는 종이Galler, Bernard A.; Fischer, Michael J. (May 1964). "An improved equivalence algorithm". Communications of the ACM. 7 (5): 301–303. doi:10.1145/364099.364331. S2CID 9034016..
^ Hopcroft, J. E.; Ullman, J. D. (1973). "Set Merging Algorithms". SIAM Journal on Computing. 2 (4): 294–303. doi:10.1137/0202024.
^ ^a ^b ^c Tarjan, Robert E.; van Leeuwen, Jan (1984). "Worst-case analysis of set union algorithms". Journal of the ACM. 31 (2): 245–281. doi:10.1145/62.2160. S2CID 5363073.
^ ^a ^b Tarjan, Robert Endre (1979). "A class of algorithms which require non-linear time to maintain disjoint sets". Journal of Computer and System Sciences. 18 (2): 110–127. doi:10.1016/0022-0000(79)90042-4.
^ ^a ^b Fredman, M.; Saks, M. (May 1989). "The cell probe complexity of dynamic data structures". Proceedings of the Twenty-First Annual ACM Symposium on Theory of Computing: 345–354. doi:10.1145/73007.73040. ISBN 0897913078. S2CID 13470414. Theorem 5: Any CPROBE(log n) implementation of the set union problem requires Ω(m α(m, n)) time to execute m Find's and n−1 Union's, beginning with n singleton sets.
^ Galil, Z.; Italiano, G. (1991). "Data structures and algorithms for disjoint set union problems". ACM Computing Surveys. 23 (3): 319–344. doi:10.1145/116873.116878. S2CID 207160759.
^ Anderson, Richard J.; Woll, Heather (1994). Wait-free Parallel Algorithms for the Union-Find Problem. 23rd ACM Symposium on Theory of Computing. pp. 370–380.
^ Conchon, Sylvain; Filliâtre, Jean-Christophe (October 2007). "A Persistent Union-Find Data Structure". ACM SIGPLAN Workshop on ML. Freiburg, Germany.
^ ^a ^b ^c Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009). "Chapter 21: Data structures for Disjoint Sets". Introduction to Algorithms (Third ed.). MIT Press. pp. 571–572. ISBN 978-0-262-03384-8.
^ 라이문드 세이델, 미카 샤리르"경로 압축의 하향식 분석", SIAM J. Comput. 34(3): 515-525, 2005
^ Tarjan, Robert Endre (1975). "Efficiency of a Good But Not Linear Set Union Algorithm". Journal of the ACM. 22 (2): 215–225. doi:10.1145/321879.321884. hdl:1813/5942. S2CID 11105749.
^ Hopcroft, J. E.; Ullman, J. D. (1973). "Set Merging Algorithms". SIAM Journal on Computing. 2 (4): 294–303. doi:10.1137/0202024.
^ 로버트 E. 타잔과 얀 반 리우웬.집합 연합 알고리즘의 최악의 경우 분석입니다.ACM 저널, 31 (2):245~281, 1984.
^ Knight, Kevin (1989). "Unification: A multidisciplinary survey" (PDF). ACM Computing Surveys. 21: 93–124. doi:10.1145/62029.62030. S2CID 14619034.
^ Automata, languages and programming : 32nd international colloquium, ICALP 2005, Lisbon, Portugal, July 11-15, 2005 ; proceedings. Luís. Caires, European Association for Theoretical Computer Science. Berlin: Springer. 2005. ISBN 978-3-540-31691-6. OCLC 262681795.{{cite book}}: CS1 유지보수: 기타 (링크)
^ Sharir, M.; Agarwal, P. (1995). Davenport-Schinzel sequences and their geometric applications. Cambridge University Press.

외부 링크

[tarjan1975-1] ^ ^a ^b ^c ^d ^e ^f Tarjan, Robert Endre (1975). "Efficiency of a Good But Not Linear Set Union Algorithm". Journal of the ACM. 22 (2): 215–225. doi:10.1145/321879.321884. hdl:1813/5942. S2CID 11105749.

[Galler1964-2] 분리된 포레스트를 발원지로 하는 종이Galler, Bernard A.; Fischer, Michael J. (May 1964). "An improved equivalence algorithm". Communications of the ACM. 7 (5): 301–303. doi:10.1145/364099.364331. S2CID 9034016..

[Hopcroft1973-3] Hopcroft, J. E.; Ullman, J. D. (1973). "Set Merging Algorithms". SIAM Journal on Computing. 2 (4): 294–303. doi:10.1137/0202024.

[Tarjan1984-4] Tarjan, Robert E.; van Leeuwen, Jan (1984). "Worst-case analysis of set union algorithms". Journal of the ACM. 31 (2): 245–281. doi:10.1145/62.2160. S2CID 5363073.

[Tarjan1979-5] Tarjan, Robert Endre (1979). "A class of algorithms which require non-linear time to maintain disjoint sets". Journal of Computer and System Sciences. 18 (2): 110–127. doi:10.1016/0022-0000(79)90042-4.

[Fredman1989-6] Fredman, M.; Saks, M. (May 1989). "The cell probe complexity of dynamic data structures". Proceedings of the Twenty-First Annual ACM Symposium on Theory of Computing: 345–354. doi:10.1145/73007.73040. ISBN 0897913078. S2CID 13470414. Theorem 5: Any CPROBE(log n) implementation of the set union problem requires Ω(m α(m, n)) time to execute m Find's and n−1 Union's, beginning with n singleton sets.

[Galil1991-7] Galil, Z.; Italiano, G. (1991). "Data structures and algorithms for disjoint set union problems". ACM Computing Surveys. 23 (3): 319–344. doi:10.1145/116873.116878. S2CID 207160759.

[Anderson1994-8] Anderson, Richard J.; Woll, Heather (1994). Wait-free Parallel Algorithms for the Union-Find Problem. 23rd ACM Symposium on Theory of Computing. pp. 370–380.

[Conchon2007-9] Conchon, Sylvain; Filliâtre, Jean-Christophe (October 2007). "A Persistent Union-Find Data Structure". ACM SIGPLAN Workshop on ML. Freiburg, Germany.

[Cormen2009-10] Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford (2009). "Chapter 21: Data structures for Disjoint Sets". Introduction to Algorithms (Third ed.). MIT Press. pp. 571–572. ISBN 978-0-262-03384-8.

[11] 라이문드 세이델, 미카 샤리르"경로 압축의 하향식 분석", SIAM J. Comput. 34(3): 515-525, 2005

[12] Tarjan, Robert Endre (1975). "Efficiency of a Good But Not Linear Set Union Algorithm". Journal of the ACM. 22 (2): 215–225. doi:10.1145/321879.321884. hdl:1813/5942. S2CID 11105749.

[13] Hopcroft, J. E.; Ullman, J. D. (1973). "Set Merging Algorithms". SIAM Journal on Computing. 2 (4): 294–303. doi:10.1137/0202024.

[14] 로버트 E. 타잔과 얀 반 리우웬.집합 연합 알고리즘의 최악의 경우 분석입니다.ACM 저널, 31 (2):245~281, 1984.

[Knight1989-15] Knight, Kevin (1989). "Unification: A multidisciplinary survey" (PDF). ACM Computing Surveys. 21: 93–124. doi:10.1145/62029.62030. S2CID 14619034.

[16] Automata, languages and programming : 32nd international colloquium, ICALP 2005, Lisbon, Portugal, July 11-15, 2005 ; proceedings. Luís. Caires, European Association for Theoretical Computer Science. Berlin: Springer. 2005. ISBN 978-3-540-31691-6. OCLC 262681795.{{cite book}}: CS1 유지보수: 기타 (링크)

[Sharir1995-17] Sharir, M.; Agarwal, P. (1995). Davenport-Schinzel sequences and their geometric applications. Cambridge University Press.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

v t 잘 알려진 데이터 구조
종류들	수집 컨테이너.
추상적인	연관 배열 멀티맵 데이터 구조 검색 목록. 스택 큐 더블 엔드 큐 priority 큐 이중 엔드 priority 큐 세트 멀티셋 디조인트 세트
어레이	비트 배열 순환 버퍼 다이내믹 어레이 해시 테이블 해시 어레이 트리 희박 행렬
링크되어 있다	어소시에이션리스트 링크 리스트 스킵 리스트 언롤링된 링크 리스트 XOR 링크 리스트
나무들	B-트리 이진 검색 트리 AA나무 AVL 트리 붉은색-검은색 셀프밸런싱 트리 스플레이 트리 히프 이진 힙 이항 힙 피보나치 힙 R 트리 R* 트리 R+ 트리 힐베르트 R-트리 트리 해시 트리
그래프	이항 결정도 방향 비순환 그래프 지시 비순환 단어 그래프
데이터 구조 목록

Search

분리 집합 데이터 구조

네임스페이스

더

목차

역사

표현

운용

새 세트 만들기

정해진 대표자를 찾는 중

두 세트의 병합

시간의 복잡성

Union-Find의 O(m log*n) 시간 복잡성 증명

적용들

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

분리 집합 데이터 구조

역사

표현

운용

새 세트 만들기

정해진 대표자를 찾는 중

두 세트의 병합

시간의 복잡성

Union-Find의 O(m log*n) 시간 복잡성 증명

적용들

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.