비르코프의 표현 정리
Birkhoff's representation theorem- 이것은 격자 이론에 관한 것이다.비슷한 이름의 다른 결과는 Birkhoff의 정리(동음이의)를 참조한다.
수학에서, Birkhoff의 분배 격자에 대한 표현 정리에서는 격자 연산이 집합의 조합과 교차점에 대응하는 방식으로, 어떤 유한 분배 격자의 요소도 유한 집합으로 나타낼 수 있다고 기술하고 있다.이 정리는 분배 격자와 부분 순서, 준순수 지식 공간과 사전 순서 사이, 또는 유한 위상학적 공간과 사전 순서 사이의 일대일 대응성을 제공하는 것으로 해석할 수 있다.그것은 1937년에 그것에 대한 증거를 출판한 개럿 비르코프의 이름을 따서 지어졌다.[1]
'버크호프의 표현 정리'라는 명칭은 버크호프의 다른 두 가지 결과에도 적용되었는데, 하나는 부울 알헤브라의 표현에 관한 것으로 1935년부터는 조합, 교차로, 보어트(Birkhoff가 분배 격자를 나타내기 위해 사용하는 집합의 고리와 밀접하게 관련됨)와 비르호프의 다른 두 가지 결과에도 적용되었다.알헤브라를 알헤브라의 산물로 나타내는 rkhoff의 HSP 정리.비르코프의 대표 정리도 유한분산 격자의 기본 정리라고 불려왔다.[2]
정리 이해
많은 격자는 격자의 요소가 집합으로 표현되고 격자의 결합 연산은 집합 결합 연조로 표현되며 격자의 충족 연산은 집합 교차로로 표현되는 방식으로 정의될 수 있다.예를 들어, 유한 집합의 모든 하위 집합의 패밀리에서 정의한 부울 격자에는 이 특성이 있다.보다 일반적으로 유한한 위상학적 공간은 그것의 열린 집합의 계열로서 집합의 격자를 가진다.집합조합과 교차로들은 분배법에 따르기 때문에, 이런 식으로 정의된 격자는 모두 분배 격자다.비르코프의 정리는 사실 모든 유한한 분배 격자는 이런 식으로 얻을 수 있다고 명시하고 있으며, 이후 비르코프 정리의 일반화는 무한 분배 격자에 대해서도 비슷한 것을 기술하고 있다.
예
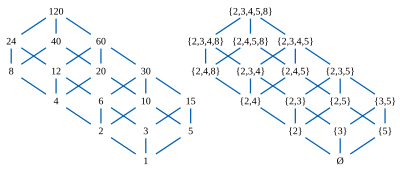
(그림에서)120과 같은 일부 복합적인 숫자의 구분점을, 부분적으로는 구별에 의해 정렬된 것으로 간주한다.12와 20과 같이 120의 두 칸은 둘 모두를 나누는 가장 큰 숫자인 12 ∧ 20 = 4의 고유한 가장 큰 공통 인수와 12 = 20 = 60의 고유한 최소 공통 배수인 12 60 20 = 60을 가지고 있다. 이 두 칸 모두 또한 120의 구분자를 가지고 있다.이 두 가지 연산 ∨과 ∧은 모든 x, y, z에 대해 (x ∧) z z = (x z z) and (y z z)와 (x ∨ y) ∧ = (x ∧ z) ∨ (y ∧ z) equivalent (y z z)의 두 가지 동등한 형태 중 하나로 분배 법칙을 만족한다.따라서, 구분자는 유한한 분배 격자를 형성한다.
각 분할자를 분할하는 주요 권한 집합과 연관시킬 수 있다. 따라서 12는 집합 {2,3,4}과(와) 관련되고 20은 집합 {2,4,5}과(와) 관련된다.그 다음 12 20 20 = 4는 세트 {2,3,4} { {2,4} = {2,4}, 12 20 20 = 60은 세트 {2,3,4} { {2,4,5} = {2,3,4,5} ∪ {2,3,4,5}}과 연관되므로 격자의 결합 및 만남 연산은 세트 조합과 교차점에 해당한다.
이들 집합에서 요소로 나타나는 주력 2, 3, 4, 5, 8은 그 자체로 부분적으로 불시에 의해 주문될 수 있다; 이 작은 부분 순서에서는 2 ≤ 4 ≤ 8이며 다른 쌍들 사이에는 순서 관계가 없다.120의 칸막이와 연관된 16 세트는 이 작은 부분 순서의 하위 집합으로, x ≤ y와 y가 하위 집합에 속할 경우 x도 하위 집합에 속해야 한다.어떤 하위 집합 L에서든 L에서 가장 일반적인 힘의 배수를 계산하여 관련 분점을 복구할 수 있다.따라서 5대 강국 2, 3, 4, 5, 8에 대한 부분 순서는 원래의 16개 소차 격자 전체를 복구하기에 충분한 정보를 담고 있다.
비르코프의 정리는 분전기의 격자 연산 ∧과 ∨과 관련된 주요 권력 집합의 연산 ∩과 ∪ 사이의 이 관계는 우연이 아니며 소수 및 불능성의 특정 속성에 의존하지 않는다: 모든 유한 분배 격자의 요소는 하위 집합과 관련될 수 있다.같은 방식으로 부분 순서의 s
또 다른 예로서, 포함에 의해 부분적으로 순서가 정해진 n-요소 집합의 하위 집합에 비르코프의 정리를 적용하면, 발전기가 n개인 자유분산 격자가 생성된다.이 격자 안의 원소의 수는 데데킨드 숫자에 의해 주어진다.
가입 비독점 순서의 일부
격자에서 원소 x는 다른 원소들의 유한 집합의 결합이 아닌 경우 결합 불가하다.마찬가지로 x는 격자의 하단 요소(영원소의 결합)나 두 개의 더 작은 원소의 결합이 아닌 경우 결합 불능이다.예를 들어, 120의 칸막이 격자에는 결합이 4인 원소 쌍이 없으므로 4는 결합-불가능하다.원소 x는 하단 원소와 다르면 조인프라임이고, x z y ∨ z는 x ≤ y 또는 x ≤ z이다.같은 격자에서 4는 조인프라임이다: lcm(y,z)가 4로 분할될 때마다 적어도 y와 z 중 하나는 4로 분할되어야 한다.
어떤 격자에서도 결합-프리미엄 요소는 결합-불가결해야 한다.마찬가지로, 결합-불가침 요소가 아닌 요소는 결합-프라임(join-preducable)이 아니다.예를 들어, 요소 x가 조인-불가침인 경우, x = y ∨ z와 같은 더 작은 y와 z가 존재한다.그러나 그 다음 x y y z z, 그리고 x는 y나 z 둘 중 하나 이상 또는 동등하지 않아 가입프라임이 아님을 보여준다.
가입-프리미엄 요소가 결합-불가침 요소의 적절한 하위 집합을 형성하는 격자가 존재하지만, 분배 격자에서는 두 유형의 요소가 일치한다.예를 들어, x가 조인-불가침이고 x ≤ y ∨ z라고 가정한다.이 불평등은 x = x ∧ (y ∨ z), 분포법 x = (x ∧ y) ∨ (x ∧ z) that (x ∧ z)라는 문구와 동등하다.그러나 x는 조인-불가침이기 때문에, x = x ∧ y (동일하게 x ≤ y) 또는 x = x ∧ z (동일하게 x ≤ z)를 보여주는 이 조인의 두 용어 중 적어도 하나는 x 그 자체여야 한다.
결합불가 요소들의 부분 집합에 대한 격자 순서는 부분 순서를 형성한다; Birkhoff의 정리는 격자 자체가 이 부분 순서의 하위 집합에서 회복될 수 있다고 말한다.
비르코프의 정리
임의의 부분적 순서에서 하한 집합은 격자를 형성하는데, 조합과 교차로들은 하위 집합이라는 특성을 보존하기 때문에, 격자의 부분적 순서가 설정된 격자를 형성하고, 결합 연산은 세트 결합에 해당하며, 충족 연산은 세트 교차점에 해당한다.집합조합과 교차로들은 분배법에 따르기 때문에, 이것은 분배 격자다.비르코프의 정리에는 어떤 유한한 분배 격자라도 이런 식으로 건설될 수 있다고 명시되어 있다.
- 정리.모든 유한분포 격자 L은 L의 결합불가 요소 부분 순서의 하위 집합의 격자와 이형성이 있다.
즉, L의 요소와 부분 순서의 하위 세트 사이에 일대일 주문 보존 서류가 있다.L의 요소 x에 해당하는 하한 집합은 단순히 x보다 작거나 같은 L의 결합 불연속 요소 집합이며, 결합 불연속 요소의 하위 집합 S에 해당하는 L의 요소는 S의 결합이다.
조인-수정 가능 요소의 하위 집합 S에 대해서는 x를 S의 결합으로 하고 T를 x보다 작거나 같은 조인-수정 가능 요소의 하위 집합으로 한다.그러면 S = T. 왜냐하면, S의 모든 요소는 분명히 T에 속하며, x보다 작거나 같은 조인 불분명한 요소는 S의 멤버 중 하나 이상이어야 하고, 따라서 (S가 더 낮은 집합이라는 가정에 의해) S 자체에 속해야 한다.반대로 L의 어떤 원소 x에 대해서도, S를 x보다 작거나 같은 결합 불분명한 원소로 하고, y를 S의 결합으로 한다.그 다음 x = y.왜냐하면, x보다 작거나 같은 원소의 결합으로서 y는 x 그 자체보다 클 수 없지만, x가 결합 불연속인 경우 x는 S에 속하고, x가 둘 이상의 결합 불연속 항목의 결합인 경우에는 다시 S에 속해야 하기 때문에 y ≥ x에 속해야 한다.따라서 서신은 일대일이고 정리가 증명된다.
세트 및 예약 주문의 링
버크호프(1937년)는 집합의 고리를 세트 유니온의 운용에 의해 폐쇄되고 교차점을 설정하는 집합의 가족으로 정의했으며, 후에 수학 심리학에서의 응용에 의해 동기 부여된 도이뇽과 팔마뉴(1999년)는 같은 구조를 준규범적 지식 공간이라고 불렀다.만약 한 세트의 링에 있는 세트들이 포함에 의해 주문된다면, 그들은 분배 격자를 형성한다.세트의 요소는 링에 설정된 일부가 y를 포함하지만 y를 포함하지 않을 때마다 x ≤ y를 포함하는 사전 순서를 지정할 수 있다.세트 링 자체는 이 사전 주문의 하위 세트 제품군이며, 어떤 사전 주문도 이러한 방식으로 세트 링을 만들어 낸다.
교감성
비르코프의 정리는 위에서 말한 바와 같이 개별적인 부분 질서와 분배 격자 사이의 일치점이다.그러나 그것은 또한 부분 주문의 주문 보존 기능과 해당 분배 격자의 경계 동형성 사이의 대응으로 확장될 수 있다.이 서신에서는 이 지도들의 방향이 뒤바뀌었다.
Let 2는 2요소 집합 {0, 1}의 부분 순서를 나타내며, 주문 관계는 0 < 1, (Stanley에 따름) J(P)는 유한 부분 순서 P의 하위 집합의 분배 격자를 나타낸다.그러면 J(P)의 요소는 P부터 2까지의 주문 보존 기능에 1 대 1로 대응한다.[2]왜냐하면, 만일 such이 그러한 함수라면 0(0−1)은 하위 집합을 형성하며, 반대로 L이 하위 집합인 경우에는 L을 0으로 매핑하고 P의 나머지 요소를 1로 매핑하는 순서 보존 함수 ƒ을L 정의할 수 있다.g가 Q에서 P까지의 주문 보존 기능인 경우, 함수 구성을 사용하여 J(P)의 요소 L을L g g로 매핑하는 J(P)에서 J(Q)까지의 함수 g*를 정의할 수 있다.이 복합함수는 Q~2를 매핑하므로 J(Q)의 g*(L) = (ƒL ∘ g)(−10) 원소에 해당한다.Further, for any x and y in J(P), g*(x ∧ y) = g*(x) ∧ g*(y) (an element of Q is mapped by g to the lower set x ∩ y if and only if belongs both to the set of elements mapped to x and the set of elements mapped to y) and symmetrically g*(x ∨ y) = g*(x) ∨ g*(y).또한 J(P)의 하단 요소(P~0의 모든 요소를 매핑하는 함수)는 g*에 의해 J(Q)의 하단 요소에 매핑되고, J(P)의 상단 요소는 g*에 의해 J(Q)의 상단 요소에 매핑된다.즉, g*는 경계 격자의 동형상이다.
단, P의 원소 자체는 J(P)부터 2까지 경계 격자 동형성(bounded lattice homorphism)과 일대일 대응한다.x가 P의 어떤 요소인 경우, x 대 1을 포함하는 모든 하위 집합과 다른 모든 하위 집합을 0으로 매핑하는 경계 격자 동형성 j를 정의할x 수 있다.And, for any lattice homomorphism from J(P) to 2, the elements of J(P) that are mapped to 1 must have a unique minimal element x (the meet of all elements mapped to 1), which must be join-irreducible (it cannot be the join of any set of elements mapped to 0), so every lattice homomorphism has the form jx for some x. Again, from any bounded latticeJ(P)에서 J(Q)까지의 동형성 h는 함수 구성을 사용하여 Q에서 P까지의 순서 보존 지도 h*를 정의할 수 있다.Q에서 P까지의 주문 보존 지도 g에 대해 g** = g, J(P)에서 J(Q)까지의 경계 격자 동형 h에 대해 h** = h가 확인될 수 있다.
범주 이론적 용어에서 J는 한편으로 유한 부분 순서와 순서 보존 지도 사이의 범주의 이중성을 정의하고, 다른 한편으로 유한 분배 격자와 경계 격자 동형성의 범주를 정의한 대립형 호몰-점자 J = Hom(-,2)이다.
일반화
무한분배 선반
무한 분포 격자에서는 결합 불능 요소의 하위 집합이 격자 요소와 일대일 대응 관계에 있는 경우가 아닐 수 있다.사실, 가입 불가침은 전혀 없을 수도 있다.예를 들어, 일반적인 구분 순서의 역순으로 정렬된 모든 자연수의 격자(그래서 y가 x를 나눌 때 x x y y): 어떤 숫자 xp와 xq의 결합으로 표현될 수 있는데 여기서 p와 q는 구별되는 소수다.그러나 무한분산 격자의 요소들은 각 격자 원소가 특정 위상학적 공간에서 콤팩트하게 열린 집합에 해당하는 일종의 스톤 이중성인 분배 격자에 대한 스톤 대표 정리를 통해 여전히 집합으로 표현될 수 있다.이 일반화된 표현 정리는 분배 격자와 스펙트럼 공간 사이의 범주-이론적 이중성(때로는 일관적인 공간이라고 하지만 선형 논리에서 일관적인 공간과는 같지 않음), 콤팩트한 오픈 세트가 교차점 아래에서 닫히고 위상의 기초를 이루는 위상학적 공간으로 표현될 수 있다.[3]힐러리 프리스틀리는 스톤의 표현 정리가 나흐빈의 순서 위상학적 공간에 대한 사상을 이용하여 부분적인 질서의 하위 집합에 의해 격자 원소를 나타내는 사상의 연장선으로 해석될 수 있음을 보여주었다.프리스틀리 분리 공리를 통해 위상과 연결된 추가적인 부분 순서가 있는 석재 공간도 경계 분배 격자를 나타내는 데 사용할 수 있다.그러한 공간은 프리스틀리 공간으로 알려져 있다.또한, 특정 비트코폴로지 공간, 즉 쌍체 스톤 공간은 추상적인 분배 격자를 나타내기 위해 한 세트의 두 개의 토폴로지를 활용하여 스톤이 원래 접근법을 일반화한다.그러므로 비르코프의 대표 정리는 최소한 세 가지 다른 방법으로 무한(경계) 분배 격자의 사례까지 확장되며, 분배 격자의 이중성 이론으로 요약된다.
버크호프의 표현 정리도 분배 격자 이외의 유한 구조로 일반화될 수 있다.분배 격자에서 자체 이중 중위수[4] 연산
중위수 대수를 생성하며 격자의 피복 관계가 중위수 그래프를 형성한다.유한 중위수 알헤브라와 중위수 그래프는 2-만족성 인스턴스(instance)의 솔루션 집합으로 이중 구조를 가지고 있으며, Barthelmy & Constantin(1993)은 혼합 그래프에서 초기 안정 집합의 집합과 동등하게 이 구조를 공식화한다.[5]분포 격자의 경우, 해당 혼합 그래프에는 방향성이 없는 가장자리가 없으며, 초기 안정 집합은 그래프의 전이성 폐쇄의 하위 집합일 뿐이다.마찬가지로, 분배 격자의 경우, 2-만족성 인스턴스의 시사 그래프는 두 개의 연결된 구성요소로 분할될 수 있다. 하나는 인스턴스의 양의 변수에 있고 다른 하나는 음의 변수에 있다. 다른 하나는 양의 구성요소의 전이적 폐쇄는 분배 격자의 기본적인 부분 순서다.
유한 결합 분배 래티 및 매트로이드
비르코프의 대표 정리와는 유사하지만, 보다 광범위한 격자에 적용되는 또 다른 결과는 유한 결합-분산형 격자를 항이마트로 나타낼 수 있다는 에델만(1980년)의 정리인데, 이 결과, 조합에 의해 폐쇄된 집합집합 계열이지만, 교차로에 따른 폐쇄가 각 비빈축적인 재산으로 대체되었다.y 세트에는 탈착 가능한 요소가 있다.
참고 항목
- 안정된 매칭의 격자, 또한 모든 유한한 분배 격자를 나타낸다.
메모들
- ^ 비르호프(1937).
- ^ a b 스탠리(1997년).
- ^ 존스톤(1982년).
- ^ 비르호프 & 키스 (1947년).
- ^ 2-SAT와 초기 안정 설정 공식 간의 사소한 차이는 후자가 비어 있는 초기 안정 집합에 해당하는 중위수 그래프에서 고정 기준점 선택을 전제로 한다는 것이다.
참조
- Barthélemy, J.-P.; Constantin, J. (1993), "Median graphs, parallelism and posets", Discrete Mathematics, 111 (1–3): 49–63, doi:10.1016/0012-365X(93)90140-O.
- Birkhoff, Garrett (1937), "Rings of sets", Duke Mathematical Journal, 3 (3): 443–454, doi:10.1215/S0012-7094-37-00334-X.
- Birkhoff, Garrett; Kiss, S. A. (1947), "A ternary operation in distributive lattices", Bulletin of the American Mathematical Society, 53 (1): 749–752, doi:10.1090/S0002-9904-1947-08864-9, MR 0021540.
- Doignon, J.-P.; Falmagne, J.-Cl. (1999), Knowledge Spaces, Springer-Verlag, ISBN 3-540-64501-2.
- Edelman, Paul H. (1980), "Meet-distributive lattices and the anti-exchange closure", Algebra Universalis, 10 (1): 290–299, doi:10.1007/BF02482912.
- Johnstone, Peter (1982), "II.3 Coherent locales", Stone Spaces, Cambridge University Press, pp. 62–69, ISBN 978-0-521-33779-3.
- Priestley, H. A. (1970), "Representation of distributive lattices by means of ordered Stone spaces", Bulletin of the London Mathematical Society, 2 (2): 186–190, doi:10.1112/blms/2.2.186.
- Priestley, H. A. (1972), "Ordered topological spaces and the representation of distributive lattices", Proceedings of the London Mathematical Society, 24 (3): 507–530, doi:10.1112/plms/s3-24.3.507, hdl:10338.dmlcz/134149.
- Stanley, R. P. (1997), Enumerative Combinatorics, Volume I, Cambridge Studies in Advanced Mathematics 49, Cambridge University Press, pp. 104–112.