버터워스 필터

선형 아날로그 전자 필터
네트워크 합성 필터 버터워스 필터 체비셰프 필터 타원(카우어) 필터 베셀 필터 가우스 필터 최적 "L"(레전드) 필터 링크비츠-릴리 필터
이미지 임피던스 필터 상수 k 필터 m유래필터 일반 이미지 필터 Zobel 네트워크(정수 R) 필터 격자 필터(모두 통과) 브리지드 T 지연 이퀄라이저(올패스) 합성 이미지 필터 mm'형 필터
심플 필터 RC 필터 RL 필터 LC 필터 RLC 필터
v t

Butterworth 필터는 통과 대역에서 가능한 한 평평한 주파수 응답을 갖도록 설계된 신호 처리 필터의 일종입니다.최대 평탄도 필터라고도 합니다.1930년 영국의 기술자이자 물리학자인 스티븐 버터워스가 "필터 증폭기 이론에 대하여"^[1]라는 논문에서 처음 기술했습니다.

원본 용지

선형 아날로그 전자 필터
네트워크 합성 필터 버터워스 필터 체비셰프 필터 타원(카우어) 필터 베셀 필터 가우스 필터 최적 "L"(레전드) 필터 링크비츠-릴리 필터
이미지 임피던스 필터 상수 k 필터 m유래필터 일반 이미지 필터 Zobel 네트워크(정수 R) 필터 격자 필터(모두 통과) 브리지드 T 지연 이퀄라이저(올패스) 합성 이미지 필터 mm'형 필터
심플 필터 RC 필터 RL 필터 LC 필터 RLC 필터
v t

버터워스는 "불가능한" 수학 문제를 푸는 것으로 정평이 나 있었다.당시 필터 설계는 이론의 한계로 인해 상당한 디자이너 경험을 필요로 했습니다.이 필터는 출판된 지 30년이 넘도록 널리 사용되지 않았다.Butterworth는 다음과 같이 말했다.

"이상적인 전기 필터는 불필요한 주파수를 완전히 거부할 뿐만 아니라 원하는 주파수에 대해 균일한 감도를 가져야 합니다."

이러한 이상적인 필터는 달성할 수 없지만, Butterworth는 올바른 값의 필터 요소의 수가 증가함에 따라 연속적으로 더 가까운 근사치를 얻을 수 있음을 보여주었다.당시 필터는 통과 대역에 상당한 리플을 발생시켰으며 구성요소 값의 선택은 매우 인터랙티브했습니다.Butterworth는 컷오프 주파수가 초당 1 라디안으로 정규화되고 주파수 응답(게인)이 다음과 같은 로우패스 필터를 설계할 수 있음을 보여주었다.

${\displaystyle G(\obmega)=syslogfrac {1}{1+{\obmega}^{2n}}}},$

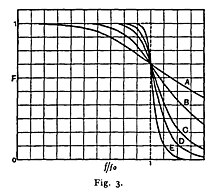
여기서$\delta {\displaystyle }$ {$displaystyle \obega}$는 초당 라디안 단위의 각 $주파수$이고$$n {\$displaystyle$ n$}$은 필터의 극 개수이며 수동 필터의 반응 요소 수에 비례합니다.${\$ \ $displaystyle$\ $obega$=$$ 1일 경우 통과 대역에서 이 유형의 필터의 진폭 응답은 1/µ2 0 0.707로, 절반의 전력 또는 -3dB입니다.Butterworth는 그의 논문에서 짝수의 극을 가진 필터만을 다루었다.그는 그러한 필터가 홀수 수의 극으로 설계될 수 있다는 것을 몰랐을 수 있다.그는 진공관 증폭기로 분리된 2극 필터로 고차 필터를 만들었습니다.2극, 4극, 6극, 8극 및 10극 필터의 주파수 응답 플롯은 원래 그래프에서 A, B, C, D 및 E로 표시됩니다.

Butterworth는 2극 필터와 4극 필터의 방정식을 풀어서 진공관 증폭기로 분리했을 때 어떻게 2극 필터와 4극 필터가 캐스케이드되는지 보여주었고, 따라서 인덕터 손실에도 불구하고 고차 필터의 구축을 가능하게 했다.1930년에는 몰리퍼몰로이 같은 저손실 코어 소재가 발견되지 않았고 공기 코어 오디오 인덕터는 오히려 손실되었습니다.Butterworth는 인덕터의 권선 저항을 보상하기 위해 필터의 성분 값을 조정할 수 있다는 것을 발견했습니다.

그는 플러그인 단자와 함께 직경 1.25㎜, 길이 3㎜의 코일 형태를 사용했다.감긴 코일 형태 안에 관련 콘덴서와 저항이 들어 있었습니다.코일은 플레이트 부하 저항기의 일부를 형성했습니다.진공관 한 개당 2개의 극이 사용되었고 다음 관의 그리드에 RC 커플링이 사용되었습니다.

또한 Butterworth는 기본 로우패스 필터를 변경하여 로우패스, 하이패스, 밴드패스 및 밴드스톱 기능을 제공할 수 있음을 보여주었습니다.

개요

Butterworth 필터의 주파수 응답은 통과 대역에서 최대 평탄하고(즉, 리플이 없음), 정지 ^[2]대역에서 0을 향해 롤오프됩니다.로그 보데 그림에서 볼 때 반응은 음의 무한대로 선형으로 기울어집니다.1차 필터의 응답은 옥타브당 -6dB(-10년당 -20dB)로 롤오프됩니다(모든 1차 로우패스 필터는 동일한 정규화 주파수 응답을 가집니다).2차 필터는 옥타브당 -12dB, 3차 필터는 -18dB 등으로 감소한다.패스밴드 및/또는 스톱밴드에 비단조 리플을 갖는 다른 필터 타입과는 달리 버터워스 필터는 δ의 단조로운 크기 함수를 가진다.

체비셰프 유형 I/Type II 필터 또는 타원 필터와 비교하여 Butterworth 필터는 롤오프가 느리기 때문에 특정 스톱밴드 사양을 구현하려면 높은 순서가 필요하지만, Butterworth 필터는 체비셰프 유형 I/Type II 및 타원 필터가 달성할 수 있는 것보다 통과 대역에서 더 선형 위상 응답을 가집니다.

예

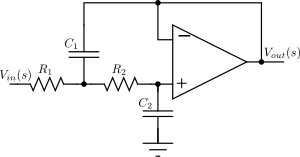
오른쪽 그림에 표시된 3차 저역 통과 Butterworth 필터 설계의 전송 함수는 다음과 같습니다.

${\displaystyle {V_{o}(s)}{V_{i}(s)}}=svfrac {R_{4}}{s^{3}(L_{1}C_{2}L_{3})+s^{2}(L_{1}C_{2}R_{4})+s(L_{1}+L_{3})_4}}}_{3}+s^{2}(L_{2})})_{2})})}}}}}}}:{{2}(L_{{{{{{{{{2})})})}.$

C2{\displaystyle C_{2}이 있는 무단계 버터 워스 필터의 단순한 예는third-order 1/4미만인 저역 디자인 오른쪽 그림에서 보여지,}=4/3 F, R4{\displaystyle R_{4}}=1Ω, L1{\displaystyle L_{1}}=3/2 H및 L3{\displaystyle L_{3}}=1/2H.[3]은 임피던스의 콘덴서. c $${{$displaystyle$ C$}$는 1$Cs)$ {{$displaystyle$ 1$/(Cs)},$ $L$의 임피던스는 $({displaystyle$$$Ls$\})$가 됩니다. $여기$서 s $=$ + ${\displaystyle j}$ {$displaystyle$ s$=\$display + $j\obe }$는 복소자 주파수이며 회로 방정식은 이 장치의 전송 함수를 산출합니다.

${\displaystyle H(s)=vfrac {V_{o}(s)}{V_{i}(s)}}=param frac {1}{1+2s+2s^{2}+s^{3}}}}.}$

주파수 응답${\displaystyle (}$게인) $G{\displaystyle }$ ( ${\displaystyle )}$) {$displaystyle$ G ( \$메가$ )}의$$ 크기는 다음과 같습니다.

${\displaystyle G(\Omega) = H(j\Omega) = flac {1} {\displayrt {1+\Omega ^{6}}}}$

에서 얻은

$\displaystyle G^{2}(\obega)=H(j\obega)=H(j\obega)\cdot H^{*}(j\obega)=hcdot frac {1}{1+\obega ^{6}}}}$

단계는 다음과 같습니다.

$(\displaystyle\Phi(\obega)=\arg(H(j\obega)).\!}$

그룹 지연은 각 주파수에 대한 위상의 도함수로 정의되며, 다른 주파수에 대한 위상 차이에 의해 발생하는 신호의 왜곡을 측정합니다.이 필터의 게인과 지연은 왼쪽 그래프에 표시됩니다.패스밴드나 스톱밴드 중 어느 쪽이든 게인곡선에 리플이 없는 것을 알 수 있다.

전송 $함수{\displaystyle }$ H${\displaystyle (s}$ $)$의 절대값 로그(\$displaystyle$ H$(s))$는 오른쪽의 두 번째 그래프에서 복잡한 주파수 공간에 표시됩니다.함수는 복잡한 주파수 평면의 왼쪽 절반에 있는 세 개의 극에 의해 정의됩니다.

$이것들$은 실제 s축과$$ 대칭인 반지름 $통일$ 원 위에 배치되어 있습니다$.$게인 함수는 원을 완성하기 위해 오른쪽 하프플레인에 3개의 극이 더 있습니다.

각 인덕터를 캐패시터로 치환하고 각 캐패시터를 인덕터로 치환함으로써 하이패스 버터워스 필터를 얻는다.

각 인덕터와 직렬로 캐패시터를 배치하고 각 캐패시터와 병렬로 캐패시터를 배치하여 공진회로를 형성함으로써 밴드패스 버터워스 필터를 얻는다.관심 주파수로 기존 구성 요소와 공명하도록 각 새 구성 요소의 값을 선택해야 합니다.

각 인덕터에 캐패시터를 병렬로 배치하고 각 캐패시터에 인덕터를 직렬로 배치하여 공진회로를 형성함으로써 밴드스톱 버터워스 필터를 얻는다.각 새 구성 요소의 값이 거부되는 주파수로 이전 구성 요소와 공진하도록 선택해야 합니다.

전송 함수

모든 필터와 마찬가지로 일반적인 프로토타입은 로우패스 필터로, 하이패스 필터로 수정하거나 다른 필터와 직렬로 배치하여 밴드패스 및 밴드스톱 필터를 형성할 수 있으며 이러한 필터의 상위 버전도 마찬가지입니다.

$n개$의$$\$displaystyle$n차$$ Butterworth 저역 필터의 $이득{\displaystyle }$ G${\displaystyle (}$ ${\displaystyle )}$)(\$displaystyle$G$(\obega)$는 전달 $함수{\displaystyle }$ H$s)$로 다음과 같이 표시됩니다.

${\displaystyle G^{2}(\displaystyle G^{2}(\displaystyle)=\left H(j\Omega)\right ^{2}}{1+\left({\frac {j\Omega}}}{2n}}}}}}}$

$여기$서$$n {\$displaystyle$ n$}$은 필터 순서, $\omega {\displaystyle {}_{}}$$$c { $displaystyle$\ $obega$_ { $c$}는$$ 컷오프 주파수(약 -3 dB 주파수), ${\displaystyle {G\mathrm{}}_{}}$0(\$displaystyle G_{0})$은 DC 게인(제로 주파수에서의 게인)

n${displaystyle$ n$}$이(가) 무한대에 $가까워짐$에 따라 게인은 직사각형 함수가 되고$,$ $gain$ G$$0$({displaystyle$ $G_{$$c})$보다 작은 주파수는 ${\displaystyle {gain\mathrm{}}_{}}$ G 0({$displaystyle$ \$obe$ G_{$0$으로 전달되며, $({$\displaystyle_mega_${c$})보다$$ 큰 주파수는 억제됨을 알 수 있습니다.$값$이 n$\displaystyle$ n이$$작을 경우 컷오프가 덜 선명해집니다.

전송 $함수{\displaystyle }$H ( $){$ $displaystyle$H ($s$ )$여기$서 ${\displaystyle s}$ ${\displaystyle =}$+ + ${\displaystyle j}${\ { $displaystyle$ s = \ display $style$ + $j$\ obega$$} (라플라스 변환에서)를 구하려고 합니다.$H{\displaystyle }$${\displaystyle {}^{}}$(${\displaystyle s^{\mathrm{}}}$ ) 2 ${\displaystyle {}^{}H}$ (${\displaystyle }$s )${\displaystyle \stackrel{}{}H\stackrel{}{}}$ (${\displaystyle \stackrel{}{s}}$ ) $¯$ {\ （ \ $displaystyle$ \$left$H ($s$ ) \ $right$^ {$2} = H$ ${\displaystyle \stackrel{}{(}}$$s$ )$$}}$$,, ,, $,,,$ ${\displaystyle =}$h${\displaystyle }$(${\displaystyle s}$ ) ,$llll$ because because because because because because because because because $because{\displaystyle }$ because because because because because because because because because because becausehh because because because because because because because because because because becauseh because because because because because because becauseh because $because$ ${\displaystyle becauseh\omega hh\stackrel{}{}}$ ${\displaystyle \mathrm{becausehh\omega }}$ becauseh ${\displaystyle \mathrm{becausej\omega }}$ becauseω becauseh $becausehh$ becauseh \ \ \ ${\displaystyle =}$ \ $다음$과 같이$재생$ 스타일 H$(s$)}:

${\displaystyle H(s)H(-s)=param frac {G_{0}^2}}{1+\left({\frac {-s^{2}}{\obe _{c}^2}}\오른쪽)^{n}}},}$

그런 다음 s ${\displaystyle =}$ ${\displaystyle j}$ {$style$ s$=j\omega$를 $사용$하면 Butterworth 필터의 주파수 응답을 얻을 수 있습니다.

$이{\displaystyle }$ 식의$n개의$극은 반지름 ${\displaystyle c_{}}$ c$$\ $displaystyle \ omega$ _ {c$}$의 원으로$$ 등간격의 점으로 나타나며 음의 실제 축을 중심으로 대칭이 됩니다.따라서 안정성을 위해 전달 기능${\displaystyle }H{\displaystyle }$ (${\displaystyle s}$ ) $\$ $displaystyle$H ($s$)이$s$의 음의 실제 하프플레인에 극만 포함되도록 선택됩니다.$k번째$극은 $다음$과$$같이$$ 지정됩니다.

${\displaystyle - {\frac {s_{k}^{2}}=param1)^{\frac {1}{n}=e^{\frac {j(2k-1)\pi }{n}}\qquad k=1,2,3,\ldots,n}$

그렇기 때문에

$\displaystyle s_{k}=\obega _{c}e^{\frac {j(2k+n-1)\pi }{2n}}\qquad k=1,2,3,\ldots,n.}$

전달(또는 시스템) 함수는 이러한 극의 관점에서 다음과 같이 기술할 수 있다.

$displaystyle H$$G_{0}\prod$ _${k=1}^{n}{\frac {{c}}{s-s_{k$

여기서 ${\$ { $displaystyle$\ $textstyle }$은 시퀀스 연산자의 산물입니다.분모는 s$\displaystyle$$s$의 Butterworth 다항식입니다.

정규화 버터워스 다항식

버터워스 다항식은 위와 같이 복잡한 형태로 작성될 수 있지만, 일반적으로 s$$ {\$displaystyle s_{1}}$ $및$ ${\displaystyle s_{}}$n {\$displaystyle s_{n$과 같은 복잡한 공역인 극 쌍을 곱하여 실제 계수로 작성된다.다항식은 ${\displaystyle c_{}}$ c ${\displaystyle {}_{}}$ { $displaystyle$\ $omega$_ {c} =$1$을 설정하면 정규화됩니다.그러면 정규화된 버터워스 다항식은 일반 곱의 형태를 갖는다.

$\displaystyle B_{n}=\prod _{k=1}^{\frac {n}{2}\cos \left [s^{2}-2s\cos \lefts\frac {2n},\pi \right}+1\qquad n=partext{even}}$

${\displaystyle B_{n}=(s+1)\prod _{k=1}^{\frac {n-1}{2}\left [s^{2}-2s\cos \lefts\frac {2n},\pi \right)+1\qad n={text}\d.}$

순서 1~10의 Butterworth 다항식의 요인은 다음 표(소수점 6자리까지)에 나와 있습니다.

n Butterworth $다항식{\displaystyle {}_{}}$ ${\displaystyle B_{}}$ ${\displaystyle n{}_{}}$(${\displaystyle }$s $){displaystyle B_{n}(s)}$의 계수 1 ${\displaystyle(s+1)}$ 2 ${\displaystyle(s^{2}+1.414214s+1)}$ 3 ${\displaystyle(s+1)(s^{2}+s+1)}$ 4 $({displaystyle (s^{2}+0.765367s+1) (s^{2}+1.847759s+1)}$ 5 $({displaystyle (s+1) (s^{2}+0.618034s+1) (s^{2}+1.618034s+1)}$ 6 $({displaystyle (s^{2}+0.517638s+1) (s^{2}+1.4142s+1) (s^{2}+1.931852s+1)}$ 7 $({displaystyle (s+1) (s^{2}+0.445042s+1) (s^{2}+1.246980s+1) (s^{2}+1.801938s+1)}$ 8 $({displaystyle (s^{2}+0.390181s+1) (s^{2}+1.11140s+1) (s^{2}+1.662939s+1) (s^{2}+1.961571s+1)$ 9 ${{displaystyle (s+1) (s^{2}+0.347296s+1) (s^{2}+1.532089s+1) (s^{2}+1.879385s+1)}$ 10 $({displaystyle (s^{2}+0.312869s+1)(s^{2}+0.907981s+1)(s^{2}+1.414214s+1)(s^{2}+1.782013s+1)(s^{2}+1.975377s+1)$

순서 1~6의 Butterworth 다항식 인자는 다음 표(정확한)에 나와 있습니다.

n Butterworth $다항식{\displaystyle {}_{}}$ ${\displaystyle B_{}}$ ${\displaystyle n{}_{}}$(${\displaystyle }$s $){displaystyle B_{n}(s)}$의 계수 1 ${\displaystyle(s+1)}$ 2 ${\displaystyle(s^{2}+{\displayrt {2}}s+1)}$ 3 ${\displaystyle(s+1)(s^{2}+s+1)}$ 4 ${\displaystyle(s^{2}+{\displayrt {2-{\displayrt {2}}}}s+1}(s^{2}+{\displayrt {2}}}s+1)}$ 5 $({displaystyle (s+1) (s^{2}+\varphi ^{-1}s+1) (s^{2}+\varphi s+1)}$ 6 $\displaystyle (s^{2}+{\displayrt {3}}}s+1) (s^{2}+{\displayrt {2}s+1) (s^{2}+{\displayrt {3}}}}s+1)$

$$서 그리스어 phi$(\displaystyle\varphi)$ 또는$$$\displaystyle\phi$는 황금 비율을 나타냅니다.2차^[4][5] $방정식{\displaystyle {}^{}}$ ${\displaystyle {x\mathrm{}}^{}}$2 -${\displaystyle }$x - ${\displaystyle 1}$ ${\displaystyle =}$ ${\displaystyle 0}$ , ${\display x^{2}-x-1=0,}$의 해인 무리수이다.

$n{displaystyle$ n}번째$$ 버터워스 다항식은 합계로도 쓸 수 있다.

${\displaystyle B_{n}=\sum _{k=0}^{n}a_{k}s^{k},,}$

재귀^[6][7] ${\displaystyle {공식}_{}}$에 의해 주어진 k$(\$}) $계수$와 함께

${\displaystyle {a_{k+1}}{a_{k}}=cos(k\display)}{\sin(k+1)\displays}}}$

그리고 제품 공식에 따라

${\displaystyle a_{k}=\display_{\mu =1}^{k}{\frac {\cos(\mu - 1)}{\sin(\mu \display}}},}$

어디에

$\displaystyle a_{0}=1\qquad\text{and}\qquad\displays =sqfrac\pi }{2n},}$

${\displaystyle {또한}_{}}$, a ${\displaystyle {}_{}}$ $=$ ${\displaystyle a_{}}$ - k (\$displaystyle a_{k$}=$a_{n-k$이다.처음 10개의 $Butterworth{\displaystyle {}_{}}$ ${\displaystyle {다항식}_{}B}$n${\displaystyle {}_{}}$( s$$)의 반올림 $계수{\displaystyle {}_{}}$ {\$displaystyle$ $a_$${k}$는 다음과$$ 같다.

Butterworth는 ${\displaystyle {소수점}_{}}$ 4자리까지 k$(\$$})$ $계수$를 계산합니다.

${\displaystyle n}$	${\displaystyle a_{0}}$	${\displaystyle a_{1}}$	${\displaystyle a_{2}}$	${\displaystyle a_{3}}$	${\displaystyle a_{4}}$	${\displaystyle a_{5}}$	${\displaystyle a_{6}}$	${\displaystyle a_{7}}$	${\displaystyle a_{8}}$	${\displaystyle a_{9}}$	${\displaystyle a_{10}}$
1	1	1
2	1	1.4142	1
3	1	2	2	1
4	1	2.6131	3.4142	2.6131	1
5	1	3.2361	5.2361	5.2361	3.2361	1
6	1	3.8637	7.4641	9.1416	7.4641	3.8637	1
7	1	4.4940	10.0978	14.5918	14.5918	10.0978	4.4940	1
8	1	5.1258	13.1371	21.8462	25.6884	21.8462	13.1371	5.1258	1
9	1	5.7588	16.5817	31.1634	41.9864	41.9864	31.1634	16.5817	5.7588	1
10	1	6.3925	20.4317	42.8021	64.8824	74.2334	64.8824	42.8021	20.4317	6.3925	1

정규화된 Butterworth 다항식을 사용하여 다음과 같이 모든 저역 통과 필터 차단 ${\displaystyle {주파수}_{}}$ µ$$c\$displaystyle \omega _{$c$\}$에 대한 전달 함수를 결정할 수 있습니다.

${\displaystyle }$$H{\displaystyle }$${\displaystyle }$(${\displaystyle s}$ ) ${\displaystyle =}$ ${\displaystyle G\frac{{}_{}}{}}$ ${\displaystyle \frac{{}_{}}{{}_{}}}$ B${\displaystyle \frac{{}_{}{n}_{}}{}}$ (${\displaystyle \frac{a}{}}$ )$$（ { $displaystyle$H ( s )$$${\displaystyle =}$ ${\displaystyle s\frac{}{}}$ ${\displaystyle \frac{{\omega }_{}}{}}$ $c$$$. \ $displaystyle$$a$$= sec$ frac { $s$$}$ { \ $메가$_ { $c$}$$} $$。$}$

다른 밴드 형태로 변환할 수도 있습니다(시제품 필터 참조).

최대 평탄도

${\displaystyle {\delta }_{}}$ c ${\displaystyle {}_{}}$ { $displaystyle$\$omega$_ {c } $=$$1$ 、 ${\displaystyle {G\mathrm{}}_{}}$ 0 $=$ ${\displaystyle 1}$ { $display$ G$_$ { 0 } $=$ 1 이라고 가정하면 주파수에 대한 이득의 도함수는 다음과 같습니다.

${\displaystyle {dG}{d\obega}}=-nG^{3}\obega^{2n-1}$

$이{\displaystyle }$ 값은 게인$$G(\$displaystyle$ G$)$가 항상 양수이므로 $모든{\displaystyle }${\(\$displaystyle\obega)$에 대해 단조롭게 감소합니다.따라서 Butterworth 필터의 게인 함수는 리플이 없습니다.이득의 일련의 확장은 다음과 같습니다.

${\displaystyle G(\obega)=1-{\frac {1}{2}}\obe ^{2n}+{\frac {3}{8}\obe ^{4n}+\ldots}$

즉, $2n번째$도함수까지의$$이득의$$ 모든 도함수는 θ $0$에서 0(\$\Omega = 0$이므로 "평탄도"가 발생합니다.단조로운 요건이 통과 대역에만 제한되고 정지 대역에서 리플이 허용되는 경우, 통과 대역에서 "최대 평탄한" 버터워스보다 평평한 역 체비셰프 필터와 같은 순서의 필터를 설계할 수 있습니다.

고주파 롤오프

다시 ${\displaystyle c_{}}$ c ${\displaystyle {}_{}}$ {$display$ \ $obega$_ { c }$$$= 1$ 을 가정하면, $큰{\displaystyle }${\ \ $displaystyle$\ $obega$} 에$$ 대한 이득 로그의 기울기는 다음과 같습니다.

${\displaystyle \lim _{\Omega \rightarrow \infty }{\frac {d\log(G)}{d\log(\omega)}}=-n.}$

따라서 데시벨 단위로 고주파 롤오프는 $(디스플레이 스타일$ n) dB$/$decade$$ 또는 $(디스플레이 스타일$ n$)$ dB$$/octave입니다(전압 게인의 제곱에 비례하므로 20의 계수가 사용됩니다. 20 로그 규칙 참조).

필터 구현 및 설계

선형 아날로그 필터를 구현하는 데 사용할 수 있는 필터 토폴로지는 여러 가지가 있습니다.패시브 실현에 가장 많이 사용되는 토폴로지는 Cauer 토폴로지입니다.액티브 실현에 가장 많이 사용되는 토폴로지는 Sallen-Key 토폴로지입니다.

코어 토폴로지

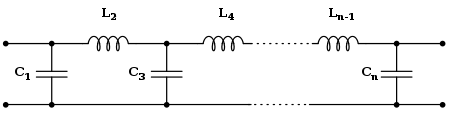
Cauer 토폴로지는 패시브 컴포넌트(분사 캐패시터 및 직렬 인덕터)를 사용하여 선형 아날로그 필터를 구현합니다.주어진 전달 기능을 가진 Butterworth 필터는 Cauer 1 양식을 사용하여 실현할 수 있습니다.k번째 요소는 다음과^[8] 같습니다.

${\displaystyle C_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k=moddtext{odd}}}$

${\displaystyle L_{k}=2\sin \left[{\frac {(2k-1)}{2n}}\pi \right]\qquad k=text{even}}}.}$

원하는 경우 필터는 직렬 인덕터로 시작할 수 있습니다. 이 경우 L은_k k 홀수이고 C는_k k 짝수입니다.이들 공식은 L과_k C를_k 모두 g로_k 함으로써 유용하게 조합할 수 있다.즉_k, g는 한계를 s로 나눈 값입니다.

$\displaystyle g_{k}=2\sin \left[{\frac {(2k-1)}{2n}\pi \right]\qquad k=1,2,3,\ldots,n.}$

이러한_c 공식은 θ = 1인 이중 종단 필터(즉, 소스와 부하 임피던스가 모두 단일성과 동일)에 적용됩니다.이 프로토타입 필터는 다른 임피던스 및 주파수 값에 맞게 스케일링할 수 있습니다.단일 종단 필터(즉, 이상적인 전압 또는 전류원에 의해 구동되는 필터)의 경우 요소 값은 다음과^[3] 같이 지정됩니다.

${\displaystyle g_{j}=bladfrac {a_{j}a_{j-1}{c_{j-1}}\qquad j=2,3,\ldots,n}$

어디에

${\displaystyle g_{1}=a_{1}}$

그리고.

$\displaystyle a_{j}=\sin \left[{\frac {(2j-1)}{2n}\pi \right]\qquad j=1,2,3,\ldots,n}$

$\displaystyle c_{j}=\cos^{2}\left[{\frac {j}{2n}\pi \right]\qquad j=1,2,3,\ldots,n.}$

전압 구동 필터는 직렬 소자로 시작하고 전류 구동 필터는 션트 소자로 시작해야 합니다.이러한 형식은 다이플렉서 및 멀티플렉서 ^[3]설계에 유용합니다.

Sallen-Key 토폴로지

Sallen-Key 토폴로지에서는 액티브컴포넌트와 패시브컴포넌트(비반전 버퍼, 통상은 op암페어, 저항기 및 캐패시터)를 사용하여 선형 아날로그 필터를 실장합니다.각 Sallen-Key 스테이지에서는 폴의 켤레 쌍이 구현됩니다.전체 필터는 모든 스테이지를 직렬로 캐스케이드하여 구현됩니다.실제 극이 있는 경우$(n\displaystyle$n이$$ 홀수인 $경우{\displaystyle }$) 이 극은 별도로 구현해야 합니다(일반적으로 RC 회로로 구현되며 액티브 스테이지와 캐스케이드되어야 합니다).

오른쪽에 표시된 2차 살렌-키 회선의 경우 전송 함수는 다음과 같습니다.

${\displaystyle H(s)=vfrac {V_{out}(s)}{V_{in}(s)}}=squalfrac {1}{1+C_{2}(R_{1}+R_{2}s+C_{1]}C_{2}R_{1}R_{2}s^{2}}}.}$

우리는 분모가 Butterworth 다항식의 2차 항 중 하나이기를 바란다.${\displaystyle c_{}}$ ${\displaystyle \mathrm{c}}$ 1 {$display$ \ $obega$_ { c }$$$= 1$ 이라고 가정하면, 이것은 다음과 같은 것을 의미합니다.

${\displaystyle C_{1}C_{2}R_{1}R_{2}=1,}$

그리고.

${\displaystyle C_{2}(R_{1}+R_{2})=-2\cos \leftflac {2k+n-1}{2n}\pi \right.}$

그러면 두 가지 정의되지 않은 성분 값이 자유롭게 선택될 수 있습니다.

살렌-키 위상이 3차 및 4차인 버터워스 로우패스 필터는 1개의 op ^[9][10]amp만을 사용하여 els스만이 설명하고, 더 높은 차수의 단일 증폭기 버터워스 필터도 쥬리시치 외 ^[11]연구진이 제공한다.

디지털 실장

Butterworth 및 기타 필터의 디지털 구현은 종종 아날로그 필터 설계를 이산화하는 두 가지 다른 방법인 쌍선형 변환 방법 또는 일치하는 Z 변환 방법을 기반으로 합니다.Butterworth 등의 전극 필터의 경우 매칭된 Z 변환법은 임펄스 불변법과 동등하다.높은 순서의 경우 디지털필터는 양자화 오류에 민감하기 때문에 종종 캐스케이드된 비쿼드 섹션과 홀수 순서의 1차 섹션 또는 3차 섹션으로 계산됩니다.

다른 선형 필터와의 비교

Butterworth 필터의 속성은 다음과 같습니다.

• 통과 대역과 정지 대역 모두에서 단조로운 진폭 응답
• 컷오프 주파수에 대한 빠른 롤오프.순서 증가에 따라 개선
• 순서 증가에 따라 악화되는 스텝 응답에서의 상당한 오버슈트 및 호출음
• 약간 비선형 위상 응답
• 그룹 지연은 주파수에 크게 의존합니다.

다음은 다른 일반적인 필터 유형 옆에 이산 시간 Butterworth 필터의 이득을 보여 주는 이미지입니다.이들 필터는 모두 5차 필터입니다.

Butterworth 필터는 체비셰프 필터 또는 타원 필터보다 컷오프 주파수 주변에서 더 느리게 롤오프되지만 리플은 없습니다.

레퍼런스