기계 에너지

기계 시스템의 예:인공위성은 보수적인 중력에만 영향을 받아 지구 궤도를 돌고 있다. 그러므로 인공위성의 기계적 에너지는 보존된다.위성의 가속도는 녹색 벡터로 나타내며 속도는 빨간색 벡터로 나타냅니다.만약 위성의 궤도가 타원형이라면, 위성의 잠재 에너지와 운동 에너지는 시간에 따라 변화하지만, 그 합계는 일정하게 유지됩니다.

물리과학에서 기계 에너지는 잠재 에너지와 운동에너지의 합이다.기계적 에너지 보존의 원리는 고립된 시스템이 보수적인 힘만을 받는다면 기계적 에너지는 일정하다는 것입니다.만약 물체가 보수적인 순력과 반대 방향으로 움직이면, 잠재 에너지는 증가할 것이고, 만약 물체의 속도가 변화한다면, 물체의 운동 에너지도 변화할 것이다.그러나 모든 실제 시스템에서는 마찰력과 같은 비보수적인 힘이 존재하지만, 그 규모가 무시할 수 있는 수준이라면 기계적 에너지는 거의 변하지 않으며 그 보존은 유용한 근사치이다.탄성 충돌에서는 운동 에너지가 보존되지만, 비탄성 충돌에서는 일부 기계적 에너지가 열에너지로 변환될 수 있습니다.손실된 기계적 에너지(방산)와 온도 상승 사이의 등가성은 제임스 프레스콧 줄에 의해 발견되었습니다.

많은 장치들이 다른 형태의 에너지로 또는 다른 형태의 에너지로 변환하는데 사용됩니다. 예를 들어, 전기 모터는 전기 에너지를 전기 에너지로 변환하고, 전기 발전기는 전기 에너지를 전기 에너지로 변환하며, 열 엔진은 열을 기계 에너지로 변환합니다.

일반

에너지는 스칼라량이고 시스템의 기계적 에너지는 잠재적 에너지(시스템 부분의 위치에 의해 측정됨)와 운동 에너지(운동 ^[1]^[2]에너지라고도 함)의 합계입니다.

\displaystyle E_{\text{mechanical}}=U+K}

위치 에너지 U는 중력이나 다른 보수적인 힘을 받는 물체의 위치에 따라 달라집니다.물체의 중력 퍼텐셜 에너지는 물체의 무게 W에 임의의 기준점에 대한 물체의 무게 중심 높이 h를 곱한 것과 같다.

U=Wh

물체의 위치 에너지는 물체의 작업 능력으로 정의될 수 있으며 물체가 ^{[nb 1]}^[1]힘의 반대 방향으로 이동함에 따라 증가한다.F가 보존력과 x 위치를 나타내는 경우, 두 위치₁ x와₂ x 사이의 힘의 위치 에너지는 x에서₁ ^[4]x까지의₂ F의 음의 적분으로 정의된다.

U=-\int_{x_{2}}{\vec {F}\cdot d{\vec {x}

운동 에너지인 K는 물체의 속도에 의존하며 움직이는 물체가 ^{[nb 2]}^[8]다른 물체와 충돌할 때 다른 물체에 작용하는 능력이다.이는 물체의 질량과 속도의 제곱의 곱의 절반으로 정의되며, 물체의 시스템의 총 운동 에너지는 ^[1]^[9]각 물체의 운동 에너지의 합입니다.

K={1 \over 2)mv^{2}

기계적 에너지 보존의 원칙은 물체나 시스템이 보존력만을 받는다면, 그 물체나 시스템의 기계적 에너지는 일정하게 ^[10]유지된다는 것입니다.보수세력과 비보수세력의 차이는 보수세력이 물체를 한 지점에서 다른 지점으로 이동할 때 보수세력에 의해 수행된 작업은 경로와 독립적이라는 것이다.반대로 비보수 세력이 물체에 작용하면 비보수 세력이 수행하는 작업은 ^[11]^[12]경로에 따라 달라집니다.

기계적 에너지 절약

기계 에너지 보존을 증명하는 MIT 교수 월터 르윈

기계적 에너지 보존 원리에 따르면 시스템에 마찰력 및 기타 비보수력이 없는 한 고립된 시스템의 기계적 에너지는 일정하게 유지됩니다.어떤 실제 상황에서든 마찰력과 다른 비보수력은 존재하지만, 많은 경우 시스템에 미치는 영향이 너무 작기 때문에 기계적 에너지 보존의 원리를 공정한 근사치로 사용할 수 있다.비록 에너지가 고립된 시스템에서 생성되거나 파괴될 수는 없지만, 그것은 다른 형태의 ^[1]^[13]에너지로 전환될 수 있다.

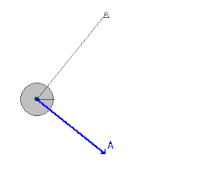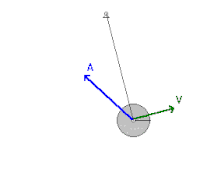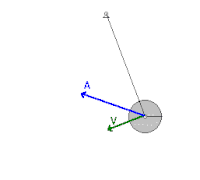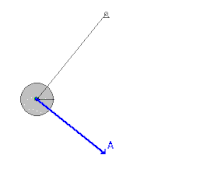
흔들리는 진자

속도 벡터(녹색)와 가속도 벡터(파란색)를 가진 흔들림 진자.진자의 속도 벡터의 크기, 속도는 수직 위치에서 가장 크고 진자는 극한 위치에서 지구에서 가장 멀리 떨어져 있습니다.

공기 항력이나 피벗에서의 마찰력 같은 마찰력이 무시할 수 있는 흔들리는 추와 같은 기계 시스템에서 에너지는 운동 에너지와 위치 에너지 사이를 왔다 갔다 하지만 절대 시스템을 벗어나지 않는다.진자는 수직 위치에 있을 때 가장 큰 운동 에너지와 가장 작은 위치 에너지에 도달합니다. 왜냐하면 진자는 이 지점에서 가장 빠른 속도를 가지고 지구에 가장 가깝기 때문입니다.반면에, 그것은 그것의 스윙의 극한 위치에 가장 적은 운동 에너지와 가장 큰 잠재 에너지를 가질 것입니다. 왜냐하면 그것은 이 지점들에서 속도가 0이고 지구에서 가장 멀리 있기 때문입니다.그러나 마찰력을 고려할 때, 시스템은 이러한 비보수적인 ^[2]힘에 의해 진자에 가해진 부정적인 작업 때문에 매번 흔들릴 때마다 기계적 에너지를 잃는다.

불가역성

시스템에서 기계적 에너지의 손실이 항상 시스템의 온도를 증가시키는 결과를 초래한다는 것은 오랫동안 알려져 왔지만, 어떻게 마찰에 대해 행해진 특정한 양의 작업이 어떻게 일정한 양의 열을 발생시키는지를 실험적으로 처음으로 증명한 사람은 아마추어 물리학자 제임스 프레스콧 줄이었다.물질을 ^[14]구성하는 입자의 무작위 운동충돌하는 물체를 고려할 때 기계적 에너지와 열의 등가성은 특히 중요합니다.탄성 충돌에서는 기계적 에너지가 보존됩니다. 충돌 물체의 기계적 에너지 합계는 충돌 전과 후에 동일합니다.그러나 비탄성 충돌 후에는 시스템의 기계적 에너지가 변경됩니다.일반적으로 충돌 전의 기계적 에너지는 충돌 후의 기계적 에너지보다 큽니다.비탄성 충돌에서는 충돌하는 물체의 기계적 에너지의 일부가 구성 입자의 운동 에너지로 변환된다.이러한 구성 입자의 운동 에너지 증가는 온도 상승으로 인식됩니다.충돌은 충돌 물체의 기계적 에너지 중 일부가 동일한 양의 열로 변환되었다고 말하는 것으로 설명할 수 있습니다.따라서 시스템의 기계적 에너지가 ^[1]^[15]감소하더라도 시스템의 총 에너지는 변경되지 않습니다.

위성.

운동

에너지

K

(\displaystyle

K

K

중력 퍼텐셜 에너지,

U

(\

displaystyle

U

)

및

U

기계

E_{\text{mechanical}}

E

(\

의

E_{\text{mechanical}}

플롯 대 R=Re, R=2*Re, R=3*Re 및 마지막 R=정지 반지름

지구 중심에서 거리 $(디스플레이$ $스타일$ r $)$ 에 $m$ 있는 질량 $K$ 의 위성은 운동 에너지 K $(디스플레이 스타일$ K $K$ 와 중력 위치 에너지 $U$ ( $디스플레이 스타일$ U $U$ 를 모두 보유하고 있다(지구 중력장 내 위치 때문에 지구의 질량은 $(\displaystyle$ M $)$ 따라서 위성-지구 시스템의 기계적 $E_{\text{mechanical}}$ E $(\$ 는 $E_{\text{mechanical}}$ 다음과 같이 주어진다.

\displaystyle E_{\text{mechanical}}=U+K}

E_{\text{mechanical}}=-G{\frac {Mm}{r}}\+{\frac {1}{2}},mv^{2}

위성이 원형 궤도에 있다면 에너지 보존 방정식은 다음과 같이 더욱 단순화될 수 있다.

E_{\text{mechanical}}=-G{\frac {Mm}{2r}

왜냐하면, 원운동에서, 뉴턴의 제2의 운동의 법칙은 다음과 같이 받아들여질 수 있기 때문이다.

\displaystyle G{\frac {Mm}{r^{2}}\ =svfrac {mv^{2}}{r}}

변환

오늘날, 많은 기술적 장치들은 기계적 에너지를 다른 형태의 에너지로 바꾸거나 그 반대입니다.이러한 디바이스는, 다음의 카테고리에 배치할 수 있습니다.

전기 모터는 전기 에너지를 기계 ^[16]^[17]^[18]에너지로 변환한다.
발전기는 기계적 에너지를 ^[19]전기에너지로 변환한다.
수력 발전소는 저수지 내 물의 기계적 에너지를 ^[20]전기에너지로 변환한다.
내연기관은 연료를 연소함으로써 화학 에너지로부터 기계적 에너지를 얻는 열기관이다.이 기계적 에너지로부터 내연기관은 종종 전기를 ^[21]생산한다.
증기 엔진은 증기의 열에너지를 기계적 ^[22]에너지로 변환한다.
터빈은 기체나 액체의 흐름의 운동 에너지를 기계적 ^[23]에너지로 변환한다.

다른 유형과의 구별

에너지를 다른 유형으로 분류하는 것은 종종 자연과학 분야의 경계를 따릅니다.

화학 에너지는 화학 결합에 "저장"된 잠재적 에너지의 일종으로 ^[24]화학에서 연구됩니다.
핵 에너지는 원자핵의 입자 사이의 상호작용에 저장되는 에너지로 ^[25]핵물리학에서 연구된다.
전자파 에너지는 전하, 자기장, 광자의 형태이다.그것은 전자기학으로 ^[26]^[27]연구되고 있다.
양자역학에서 다양한 형태의 에너지. 예를 들어 원자 ^[28]^[29]내 전자의 에너지 수준입니다.

레퍼런스

메모들

^ 기계 에너지를 측정할 때, 아이작 뉴턴이 그의 원칙에서 말한 것과 같이, 물체가 전체적으로 고려된다는 것을 주목하는 것이 중요하다: "전체 운동은 부품의 움직임의 합과 같다; 즉, 그들의 위치에서 그것의 부분의 위치가 바뀌어서 전체 위치의 합과 같다.부품의 에이스가 내장되어 있고 ^[3]전신에 있습니다."
^ 물리학에서 속도는 스칼라량이고 속도는 벡터이다.속도는 방향에 따른 속도이며, 속도가 ^[5]^[6]^[7]속도의 수치 크기이기 때문에 물체의 속도를 바꾸지 않고 변화할 수 있습니다.

인용문

^ ^a ^b ^c ^d ^e Wilczek, Frank (2008). "Conservation laws (physics)". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-08-26.
^ ^a ^b "mechanical energy". The New Encyclopædia Britannica: Micropædia: Ready Reference. Vol. 7 (15th ed.). 2003.
^ 뉴턴 1999, 페이지 409
^ "Potential Energy". Texas A&M University–Kingsville. Archived from the original on 2012-04-14. Retrieved 2011-08-25.
^ Brodie 1998, 페이지 129–131 harvnb 오류: 대상 없음: CITREFBrodie 1998 (도움말)
^ Rusk, Rogers D. (2008). "Speed". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-08-28.
^ Rusk, Rogers D. (2008). "Velocity". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-08-28.
^ Brodie 1998, 페이지 101 harvnb 오류: 대상 없음: CITREFBrodie 1998(도움말)
^ Jain 2009, 페이지 9
^ Jain 2009, 페이지 12
^ Department of Physics. "Review D: Potential Energy and the Conservation of Mechanical Energy" (PDF). Massachusetts Institute of Technology. Retrieved 2011-08-03.
^ Resnick, Robert and Halliday, David(1966), 물리 섹션 8-3(Vol I 및 II, 복합판), Wiley International Edition, 의회도서관 카탈로그 카드 No. 66-11527
^ E. Roller, Duane; Leo Nedelsky (2008). "Conservation of energy". AccessScience. McGraw-Hill Companies. Retrieved 2011-08-26.
^ "James Prescott Joule". Scientists: Their Lives and Works. Gale. 2006. 에 인용한 바와 같이
^ Schmidt, Paul W. (2008). "Collision (physics)". AccessScience. McGraw-Hill Companies. Retrieved 2011-09-03.
^ Kopicki, Ronald J. (2003). "Electrification, Household". In Kutler, Stanley I. (ed.). Dictionary of American History. Vol. 3 (3rd ed.). New York: Charles Scribner's Sons. pp. 179–183. 에 인용한 바와 같이
^ Lerner, K. Lee; Lerner, Brenda Wilmoth, eds. (2008). "Electric motor". The Gale Encyclopedia of Science (4th ed.). Detroit: Gale. 에 인용한 바와 같이
^ "Electric motor". U*X*L Encyclopedia of Science. U*X*L. 2007. 에 인용한 바와 같이
^ "Generator". U*X*L Encyclopedia of Science. U*X*L. 2007-07-16. 에 인용한 바와 같이
^ "Hydroelectric Power". Water Encyclopedia. 2013-08-23 취득
^ Lerner, K. Lee; Lerner, Brenda Wilmoth, eds. (2008). "Internal combustion engine". The Gale Encyclopedia of Science (4th ed.). Detroit: Gale. 에 인용한 바와 같이
^ "Steam engine". U*X*L Encyclopedia of Science. U*X*L. 2007-07-16. 에 인용한 바와 같이
^ Lerner, K. Lee; Lerner, Brenda Wilmoth, eds. (2008). "Turbine". The Gale Encyclopedia of Science (4th ed.). Detroit: Gale. 에 인용한 바와 같이
^ Atkins, Peter W. (2008). "Chemical energy". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.
^ Duckworth, Henry E.; Wilkinson, D. H. (2008). "Nuclear binding energy". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.
^ Hartwig, William H. (2008). "Electrical energy measurement". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.
^ Smythe, William R. (2008). "Electromagnetic radiation". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.
^ Gerjuoy, Edward (2008). "Quantum mechanics". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.
^ March-Russell, John (2008). "Energy level (quantum mechanics)". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.

참고 문헌

Brodie, David; Brown, Wendy; Heslop, Nigel; Ireson, Gren; Williams, Peter (1998). Terry Parkin (ed.). Physics. Addison Wesley Longman Limited. ISBN 978-0-582-28736-5.
Jain, Mahesh C. (2009). Textbook of Engineering Physics, Part I. New Delhi: PHI Learning Pvt. Ltd. ISBN 978-81-203-3862-3. Retrieved 2011-08-25.
Newton, Isaac (1999). I. Bernard Cohen; Anne Miller Whitman (eds.). The Principia: mathematical principles of natural philosophy. United States of America: University of California Press. ISBN 978-0-520-08816-0.

[4] 기계 에너지를 측정할 때, 아이작 뉴턴이 그의 원칙에서 말한 것과 같이, 물체가 전체적으로 고려된다는 것을 주목하는 것이 중요하다: "전체 운동은 부품의 움직임의 합과 같다; 즉, 그들의 위치에서 그것의 부분의 위치가 바뀌어서 전체 위치의 합과 같다.부품의 에이스가 내장되어 있고 ^[3]전신에 있습니다."

[9] 물리학에서 속도는 스칼라량이고 속도는 벡터이다.속도는 방향에 따른 속도이며, 속도가 ^[5]^[6]^[7]속도의 수치 크기이기 때문에 물체의 속도를 바꾸지 않고 변화할 수 있습니다.

[Access_CL-1] Wilczek, Frank (2008). "Conservation laws (physics)". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-08-26.

[Britannica_mechE-2] "mechanical energy". The New Encyclopædia Britannica: Micropædia: Ready Reference. Vol. 7 (15th ed.). 2003.

[Newton409-3] 뉴턴 1999, 페이지 409

[tamuk-5] "Potential Energy". Texas A&M University–Kingsville. Archived from the original on 2012-04-14. Retrieved 2011-08-25.

[Brodie129-131-6] Brodie 1998, 페이지 129–131 harvnb 오류: 대상 없음: CITREFBrodie 1998 (도움말)

[AccessSp-7] Rusk, Rogers D. (2008). "Speed". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-08-28.

[AccessVe-8] Rusk, Rogers D. (2008). "Velocity". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-08-28.

[Brodie101-10] Brodie 1998, 페이지 101 harvnb 오류: 대상 없음: CITREFBrodie 1998(도움말)

[Jain9-11] Jain 2009, 페이지 9

[Jain12-12] Jain 2009, 페이지 12

[MIT_Physics-13] Department of Physics. "Review D: Potential Energy and the Conservation of Mechanical Energy" (PDF). Massachusetts Institute of Technology. Retrieved 2011-08-03.

[14] Resnick, Robert and Halliday, David(1966), 물리 섹션 8-3(Vol I 및 II, 복합판), Wiley International Edition, 의회도서관 카탈로그 카드 No. 66-11527

[Access_CoE-15] E. Roller, Duane; Leo Nedelsky (2008). "Conservation of energy". AccessScience. McGraw-Hill Companies. Retrieved 2011-08-26.

[16] "James Prescott Joule". Scientists: Their Lives and Works. Gale. 2006. 에 인용한 바와 같이

[Access_Cp-17] Schmidt, Paul W. (2008). "Collision (physics)". AccessScience. McGraw-Hill Companies. Retrieved 2011-09-03.

[18] Kopicki, Ronald J. (2003). "Electrification, Household". In Kutler, Stanley I. (ed.). Dictionary of American History. Vol. 3 (3rd ed.). New York: Charles Scribner's Sons. pp. 179–183. 에 인용한 바와 같이

[19] Lerner, K. Lee; Lerner, Brenda Wilmoth, eds. (2008). "Electric motor". The Gale Encyclopedia of Science (4th ed.). Detroit: Gale. 에 인용한 바와 같이

[20] "Electric motor". U*X*L Encyclopedia of Science. U*X*L. 2007. 에 인용한 바와 같이

[21] "Generator". U*X*L Encyclopedia of Science. U*X*L. 2007-07-16. 에 인용한 바와 같이

[22] "Hydroelectric Power". Water Encyclopedia. 2013-08-23 취득

[23] Lerner, K. Lee; Lerner, Brenda Wilmoth, eds. (2008). "Internal combustion engine". The Gale Encyclopedia of Science (4th ed.). Detroit: Gale. 에 인용한 바와 같이

[24] "Steam engine". U*X*L Encyclopedia of Science. U*X*L. 2007-07-16. 에 인용한 바와 같이

[25] Lerner, K. Lee; Lerner, Brenda Wilmoth, eds. (2008). "Turbine". The Gale Encyclopedia of Science (4th ed.). Detroit: Gale. 에 인용한 바와 같이

[26] Atkins, Peter W. (2008). "Chemical energy". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.

[27] Duckworth, Henry E.; Wilkinson, D. H. (2008). "Nuclear binding energy". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.

[28] Hartwig, William H. (2008). "Electrical energy measurement". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.

[29] Smythe, William R. (2008). "Electromagnetic radiation". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.

[30] Gerjuoy, Edward (2008). "Quantum mechanics". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.

[31] March-Russell, John (2008). "Energy level (quantum mechanics)". AccessScience. McGraw-Hill Companies. Archived from the original on 2013-07-19. Retrieved 2011-10-17.

[1]

[2]

[nb 1]

[4]

[nb 2]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[3]

[5]

[6]

[7]

v t 에너지
개요 역사 색인
근본적인 개념	에너지 단위 에너지 절약 에너지학 에너지 변환 에너지 상태 에너지 이행 에너지 레벨 에너지 시스템 덩어리 음질량 질량-에너지 등가 힘 열역학 양자 열역학 열역학의 법칙 열역학계 열역학 상태 열역학 퍼텐셜 열역학적 자유 에너지 돌이킬 수 없는 프로세스 서멀 리저버 열전달 열용량 볼륨(열역학) 열역학 평형 열평형 열역학적 온도 격리 시스템 엔트로피 자유 엔트로피 엔트로피력 네겐트로피 일하다. 엑서지 엔탈피
종류들	키네틱 내부의 온도 잠재적인 중력 탄성 전위 에너지 기계 원자간 전위 양자 퍼텐셜 전기 마그네틱 이온화 빛나다 바인딩 핵결합 에너지 중력 결합 에너지 양자 색역학 결합 에너지 어두운 퀸텐스 팬텀 아니요. 화학의 쉬다 음향 에너지 표면 에너지 진공 에너지 제로 포인트 에너지 양자 퍼텐셜 양자 변동
에너지 캐리어	방사능 엔탈피 기계파 음파 연료 화석 연료 수소 수소 연료 열 잠열 일하다. 전기 배터리 콘덴서
일차 에너지	화석 연료 석탄 석유 천연가스 핵연료 천연 우라늄 복사 에너지 태양의 바람 수력 발전 해양 에너지 지열 바이오 에너지 중력 에너지
에너지 시스템 구성 요소들	에너지 엔지니어링 정유소 전력 화석연료 발전소 열병합발전 통합 가스화 복합 사이클 원자력 원자력 발전소 방사성 동위원소 열전 발전기 태양광 발전 태양광 발전 시스템 집광 태양 에너지 태양열 에너지 태양광 발전탑 태양열로 풍력 발전 풍력 발전 풍력 에너지 수력 발전 수력 전기 웨이브 팜 조력 지열 발전 바이오매스
사용 및 공급.	소비 전력 에너지 저장소 세계 에너지 소비량 에너지 보안 에너지 절약 효율적인 에너지 사용 운송 농업 재생 에너지 지속 가능한 에너지 에너지 정책 에너지 개발 전 세계 에너지 공급 남미 미국 멕시코 캐나다 유럽 아시아 아프리카 호주.
기타	제본스의 역설 탄소 배출량
카테고리 공통 포털 위키프로젝트

Search