보수 세력

시리즈의 일부
고전 역학
$({displaystyle {textbf {F}}=squalfrac {d}{dt}})(m*textbf {v}})$ 운동 제2법칙
역사 타임라인 교재
나뭇가지 응용의 천상의 연속체 다이내믹스 운동학 동력학 스태틱스 통계
기초 액셀러레이션 각운동량 커플 달랑베르의 원리 에너지 동적인 잠재적인 힘. 기준범위 관성 기준 프레임 충동 관성/관성 모멘트 덩어리 기계력 기계 작업 순간. 모멘텀 공간 스피드 시간을 토크 속도 가상 작업
제제 뉴턴의 운동 법칙 해석역학 라그랑주 역학 해밀턴 역학 루시아 역학 해밀턴-야코비 방정식 아펠 운동 방정식 쿱만-본 노이만 역학
주요 토픽 감쇠비 변위 운동 방정식 오일러의 운동 법칙 가공의 힘 마찰 고조파 발진기 관성/비관성 기준 프레임 평면 입자 운동 역학 움직임(선형) 뉴턴의 만유인력의 법칙 뉴턴의 운동 법칙 상대 속도 강체 역학 오일러 방정식 단순 고조파 운동 진동
회전 원운동 회전 기준 프레임 구심력 원심력 반응성 코리올리 힘 진자 접선 속도 회전 속도 각도 가속도/변위/주파수/속도
과학자 케플러 갈릴레오 호이겐스 뉴턴 경이다. 호록스 핼리 모페르튀이 다니엘 베르누이 요한 베르누이 오일러 달랑베르 클라이어트 라그랑주 라플라스 해밀턴 포아송 코시 러스 리우빌 어필 깁스 쿠프만 폰 노이만
물리 포털 카테고리
v t

물리학에서, 보존력은 두 점 사이의 입자를 이동시키는 총 작업이 ^[1]정해진 경로와 독립적이라는 특성을 가진 힘이다.마찬가지로 입자가 닫힌 루프 내에서 이동하면 총 작업량(경로를 따라 작용하는 힘에 변위를 곱한 합)에 보존력은 ^[2]0이 된다.

보존력은 물체의 위치에만 의존합니다.힘이 보수적이면, 어떤 점에서든 전위에 대한 수치를 할당할 수 있고, 반대로 물체가 한 위치에서 다른 위치로 이동할 때, 힘은 물체의 전위에너지를 이동 경로에 의존하지 않는 양만큼 변화시켜 기계적 에너지와 ENe의 전반적인 보존에 기여한다.rgy. 힘이 보수적이지 않으면 스칼라 전위를 정의할 수 없습니다. 왜냐하면 다른 경로를 택하면 시작점과 끝점 사이에 상충하는 전위차가 생기기 때문입니다.

중력은 보수적인 힘의 한 예이고 마찰력은 비보수적인 힘의 한 예이다.

보존력의 다른 예로는 탄성 스프링의 힘, 두 전하 사이의 정전기력, 두 자극 사이의 자기력이 있습니다.마지막 두 힘은 두 개의 대전/자화 물체의 중심을 연결하는 선을 따라 작용하기 때문에 중심력이라고 불립니다.중심력은 구면적으로 ^[3]대칭인 경우에만 보수적이다.

비공식 정의

비공식적으로, 보수적인 힘은 기계적 에너지를 보존하는 힘이라고 생각할 수 있다.입자가 점 A에서 시작되고 이에 작용하는 힘 F가 있다고 가정합니다.그리고 입자는 다른 힘에 의해 움직이며 결국 다시 A에 도달한다.입자는 여전히 움직이고 있을 수 있지만, 다시 A 지점을 지날 때, 그것은 닫힌 경로를 이동한 것입니다.이 시점에서 F가 수행한 순작업이 0일 경우 F는 폐쇄 경로 테스트를 통과합니다.가능한 모든 닫힌 경로에 대해 닫힌 경로 시험을 통과하는 힘은 보존력으로 분류된다.

중력, 스프링력, 자력(아래의 정의에 따르면)과 전기력(최소한 시간 독립 자기장에서는 패러데이의 유도 법칙 참조)은 보존력의 예이며 마찰력과 공기 항력은 보존력이 아닌 힘의 고전적인 예다.

비보수적인 힘의 경우, 손실된(보존되지 않은) 기계적 에너지는 에너지 보존에 의해 다른 곳으로 이동해야 합니다.일반적으로 에너지는 열로 변환됩니다. 예를 들어 마찰에 의해 발생하는 열입니다.열뿐만 아니라 마찰은 종종 약간의 소리 에너지를 만들어 냅니다.움직이는 보트의 물 끌기는 보트의 기계적 에너지를 열과 소리 에너지뿐만 아니라 가장자리에 있는 파동 에너지로 변환합니다.열역학 제2법칙 때문에 이러한 에너지 손실과 다른 에너지 손실은 되돌릴 수 없습니다.

경로 독립성

폐쇄 경로 시험의 직접적인 결과는 두 지점 사이를 이동하는 입자에 대한 보존력에 의해 수행된 작업이 입자가 취하는 경로에 의존하지 않는다는 것이다.

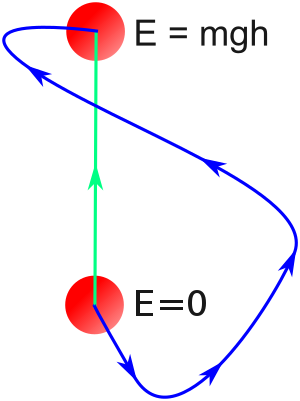
이것은 오른쪽 그림에 나타나 있습니다.물체에 대한 중력에 의한 작업은 중력이 보수적이기 때문에 물체의 높이 변화에만 의존합니다.보수 세력에 의해 수행된 작업은 그 과정 동안 잠재 에너지 변화의 부정과 같다.예를 들어, A 지점에서 B 지점으로 가는 두 개의 경로 1과 2를 상상해 보십시오.경로 1을 A에서 B로, 경로 2를 B에서 A로 역행하는 입자의 에너지 변동은 0이다. 따라서 작업은 경로 1과 2에서 동일하다. 즉, A에서 B로 이동하는 한, 작업은 뒤따르는 경로와 독립적이다.

예를 들어 어린이가 마찰 없이 미끄러져 내려오는 경우 슬라이드의 시작부터 끝까지 아이에 대한 중력에 의한 작업은 슬라이드의 모양과는 무관하며 어린이의 수직 변위에만 의존합니다.

수학적 설명

공간의 모든 곳(또는 단순히 연결된 공간의 볼륨 내)에서 정의되는 힘장 F는 다음 세 가지 동등한 조건 중 하나를 충족하면 보존력 또는 보존 벡터장이라고 불립니다.

1. F의 컬은 제로 벡터입니다.
   $${\displaystyle} {\vec {F}} =\vec {0}.}$$

   
   여기서 2차원에서 이것은 다음과 같이 감소한다.
   $${\displaystyle {\frac F_{y} {\partial x}}-{\frac F_{x} {\partial y}=0}$$

   
2. 같은 장소에서 시작 및 종료되는 궤적을 통해 입자를 이동할 때 힘에 의해 수행되는 순작업(W)은 제로입니다.
   $$\displaystyle W\equiv \point _{C}{\vec {F}}\cdot \mathrm {d}{vec {r}}=0.}$$

   
3. 힘은 전위의 음의 구배 $(\displaystyle \Phi$로 나타낼 수 있습니다.
   $$(\displaystyle {F}}=-{\vec {\vec}}\Phi .}$$

   

보수세력이라는 용어는 보수세력이 존재할 때 기계적 에너지를 절약한다는 사실에서 유래했다.가장 친숙한 보존력은 중력, 전기력(시간 독립 자기장에서는 패러데이의 법칙 참조), 스프링력입니다.

많은 힘(특히 속도에 의존하는 힘)은 힘장이 아니다.이 경우 위의 세 가지 조건은 수학적으로 동일하지 않습니다.예를 들어 자력은 조건 2(하전입자에 대한 자계에 의한 작업이 항상 0이기 때문에)를 만족시키지만 조건 3을 만족시키지 못하고, 조건 1은 정의되지도 않는다(힘은 벡터장이 아니므로 그 컬을 평가할 수 없다).따라서 자기력을 보수적으로 분류하는 ^[4]저자가 있는가 하면 그렇지 않은 ^[5]저자도 있다.자기력은 특이한 경우입니다. 마찰력과 같은 대부분의 속도 의존력은 세 가지 조건 중 어느 것도 만족시키지 못하기 때문에 명백하게 비보수적입니다.

비보수 세력

총 에너지의 보존에도 불구하고, 고전 물리학에서 비 보존력은 무시된 자유도 또는 ^[6]시간에 의존하는 잠재력으로부터 발생할 수 있다.많은 비보수 세력은 소규모 보수 ^[7]세력의 거시적 효과로 인식될 수 있다.예를 들어, 마찰은 개별 분자의 움직임을 고려함으로써 에너지 보존을 침해하지 않고 처리될 수 있다. 그러나, 그것은 통계적 방법을 통해 처리하는 것보다 모든 분자의 움직임을 고려해야 한다는 것을 의미한다.거시적 시스템의 경우 수백만 개의 자유도보다 비보수적 근사치를 다루기가 훨씬 쉽다.

비보수력의 예로는 마찰력과 비탄성 재료 응력이 있다.마찰은 신체의 큰 움직임에서 작은 움직임으로 에너지의 일부를 전달하는 효과가 있으며, 따라서 ^[7]대규모로 비보수적으로 보인다.일반상대성이론은 수성 ^{[citation needed]}궤도의 비정상적인 세차운동에서 볼 수 있듯이 비보수적이다.그러나 일반상대성이론은 응력-에너지-모멘텀 유사센서를 보존한다.

「 」를 참조해 주세요.

• 보수 벡터장
• 보수적 제도

레퍼런스