돌이킬 수 없는 프로세스

열역학
고전적인 카르노 히트 엔진
나뭇가지 고전적인 통계 화학의 양자 열역학 평형/비평형
법률 제로스 첫번째 둘째 셋째
시스템들 폐쇄형 시스템 오픈 시스템 격리 시스템 주 상태 방정식 이상 기체 실가스 상황 위상(매터) 평형 볼륨 제어 인스트루먼트 과정 이소바릭 아이소코리 등온 단열성 등엔트로픽 이센탈픽 준정전성 폴리트로픽 자유 확장 가역성 불가역성 내복원성 사이클 히트 엔진 히트 펌프 열효율
시스템 속성 주의: 이탤릭체로 표시된 켤레 변수 속성도 집약적이고 광범위한 속성 프로세스 기능 일하다. 열 국가 기능 온도/엔트로피(개요) 압력/볼륨 화학 퍼텐셜/입자수 증기 품질 속성 감소
재료 특성 속성 데이터베이스 비열 용량 ${\displaystyle c=}$ ${\displaystyle T}$ $\displaystyle \partial S\$ ${\displaystyle N}$ ${\displaystyle\partial T}$ 압축성 $\displaystyle \displays =-}$ ${\displaystyle 1}$ ${\displaystyle\partial V}$ ${\displaystyle V}$ $(\displaystyle\displayp)$ 열팽창 $\displaystyle \alpha =}$ ${\displaystyle 1}$ ${\displaystyle\partial V}$ ${\displaystyle V}$ ${\displaystyle\partial T}$
방정식 카르노의 정리 클라우시우스 정리 기본 관계 이상기체의 법칙 맥스웰 관계 온사저 호혜 관계 브리지만 방정식 열역학 방정식 표
가능성 자유 에너지 자유 엔트로피 내부 에너지 ${\displaystyle U(S,V)}$ 엔탈피 ${\displaystyle H(S,p)=U+pV}$ 헬름홀츠 자유 에너지 ${\displaystyle A(T,V)=U-TS}$ 깁스 자유 에너지 ${\displaystyle G(T,p)=H-TS}$
역사 문화 역사 일반 엔트로피 가스 법칙 "영구 운동" 기계 철학 엔트로피와 시간 엔트로피와 생명 브라운 래칫 맥스웰의 악마 열사 역설 로슈미트의 역설 시너제틱스 이론들 열량론 Vis viva ('생체력') 열의 기계적 등가 동력 주요 출판물 실험적인 질문 ~에 대해서열 균형에 대하여 이종 물질 의 리플렉션 불의 원동력 타임라인 열역학 히트 엔진 예체능 교육 맥스웰의 열역학 표면 에너지 분산으로서의 엔트로피
과학자 베르누이 볼츠만 브리지만 카라테오도리 카르노 클라피론 클라우시우스 돈더 듀헴 깁스 폰 헬름홀츠 줄 루이스 마시외 맥스웰 폰 메이어 네른스트 온사게 플랑크 랭킨 스미톤 스틸 태트 톰슨 톰슨 판 데르 발스 워터스톤
다른. 핵생성 자가 조립 자기 조직화 질서와 무질서
카테고리
v t

과학에서는 돌이킬 수 없는 과정을 돌이킬 수 없는 과정이라고 부른다.이 개념은 열역학에서 자주 발생한다.공존 온도(예: 물 속의 얼음 녹임)에서의 상전이는 가역적으로 근사하지만, 모든 복잡한 자연 과정은 되돌릴 ^[1][2][3][4]수 없다.

열역학에서, 시스템의 열역학 상태와 그 주변의 모든 상태의 변화는 에너지를 소비하지 않고 시스템의 일부 속성의 미세한 변화에 의해 정확하게 초기 상태로 회복될 수 없다.돌이킬 수 없는 프로세스를 거친 시스템은 초기 상태로 돌아갈 수 있습니다.엔트로피는 상태 함수이기 때문에 프로세스가 가역적이든 비가역적이든 시스템의 엔트로피 변화는 동일합니다.그러나 환경을 초기 상태로 복원하는 것은 불가능합니다.돌이킬 수 없는 과정은 시스템과 그 주변의 총 엔트로피를 증가시킨다.열역학 제2법칙은 가상의 과정이 가역적인지 아닌지를 결정하기 위해 사용될 수 있다.

직감적으로, 산산이 없다면 프로세스는 되돌릴 수 있습니다.예를 들어, 처음에는 시스템이 균일하지 않기 때문에 줄 확장은 되돌릴 수 없습니다.처음에는 가스가 들어 있는 시스템과 가스가 들어 있지 않은 시스템의 일부가 있습니다.낭비가 발생하기 위해서는 이러한 불균일성이 필요합니다.이는 시스템에서 가스의 한 부분은 뜨겁고 다른 한 부분은 차가웠던 것과 같습니다.그러면 소산이 발생합니다.작업이 이루어지지 않고 온도 분포가 균일해집니다.또한 열을 추가하거나 제거할 수 없으며 시스템을 초기 상태로 되돌리기 위해 볼륨을 변경할 수 없기 때문에 되돌릴 수 없습니다.따라서 시스템이 항상 균일한 경우 프로세스는 가역적입니다.즉, 열을 추가 또는 제거하거나 시스템에서 작업을 수행하거나 시스템이 작동하도록 함으로써 시스템을 원래 상태로 되돌릴 수 있습니다.또 다른 예로 내연기관의 팽창을 가역적으로 근사하기 위해 스파크 후 부피 전체에 걸쳐 온도와 압력이 균일하게 변화한다고 가정합니다.분명히, 이것은 사실이 아니며, 불꽃이 전방에서 일어나고 때로는 엔진 노크도 있습니다.디젤 엔진이 더 높은 효율을 달성할 수 있는 이유 중 하나는 연소가 훨씬 균일하기 때문에 에너지 손실이 적고 프로세스가 가역성에 ^{[citation needed]}가깝기 때문입니다.

돌이킬 수 없는 현상은 만약 충분히 복잡한 시스템인 열역학 시스템이 하나의 열역학 상태에서 다른 열역학 상태로 옮겨진다면, 시스템 내의 원자와 분자의 구성이나 배열은 쉽게 예측할 ^[5][6]수 없는 방식으로 바뀔 것이다.어떤 "변환 에너지"는 "일하는 기관"의 분자가 한 상태에서 다른 상태로 변할 때 서로 작용하기 때문에 사용될 것이다.이 변환 중에는 분자간 마찰 및 충돌로 인해 열 에너지 손실 또는 소산이 발생합니다.이 에너지는 프로세스가 역전되면 회수할 수 없습니다.

한 때 되돌릴 수 있다고 생각되었던 많은 생물학적 과정들이 실제로 두 가지 돌이킬 수 없는 과정의 쌍인 것으로 밝혀졌습니다.한 때 단일 효소가 화학 변화를 전진과 역방향으로 촉매한다고 믿었던 반면, 연구는 열역학적으로 돌이킬 수 없는 한 쌍의 ^[7]과정을 수행하기 위해 유사한 구조의 두 개의 분리된 효소가 일반적으로 필요하다는 것을 발견했다.

절대값과 통계값의 가역성

이 섹션에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 기사는 초점이 없거나 여러 주제에 대한 것일 수 있습니다. 기사를 분할하거나 명확화 페이지를 도입하거나 토크 페이지에서 이 문제를 논의하여 이 기사를 개선해 주십시오.(2014년 4월) 이 섹션은 독자들에게 혼란스럽거나 불분명할 수 있습니다. 섹션을 명확하게 하는 데 도움을 주세요. 토크 페이지에 이 건에 대한 논의가 있을 수 있습니다.(2014년 4월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

열역학은 다수의 실체의 통계적 행동을 정의하며, 그 정확한 행동은 보다 구체적인 법칙에 의해 주어진다.물리학의 기본 이론 법칙은 모두 시간적으로 되돌릴 ^[8]수 있는 반면, 실제 가역성의 확률은 낮고 시스템과 주변 환경의 이전 상태는 어느 정도만 회복된다(불확실성 원리 참조).열역학의 가역성은 본질적으로 통계적이어야 한다. 즉, 시스템의 엔트로피가 낮아질 가능성은 매우 낮지만 불가능하지는 않아야 한다.즉, 시간이 역방향으로 흐르거나 프로세스의 상태 순서가 역방향(마지막 상태가 첫 번째 상태가 되고 그 반대도 마찬가지)일 경우 시간 가역성이 실현됩니다.

역사

1850년대 독일의 물리학자 루돌프 클라우시우스는 엔트로피 개념을 도입함으로써 자연에서 돌이킬 수 없는 발견을 수학적으로 수치화한 최초의 인물이다.클라우시우스는 1854년 회고록 "열기의 기계적 이론에서 두 번째 기본 정리의 수정된 형태에 대하여"에서 다음과 같이 말한다.

또한 동일한 프로세스에서 상승 전달을 수반하는 열의 하강 전달 대신 유사한 종류의 새로운 영구 변화로 대체되거나 하강 전달을 생성하지 않으면 되돌릴 수 없는 특성을 가진 또 다른 영구 변화가 발생할 수 있다.n의 열

간단히 말해서, Clausius는 시스템이 더 차가운 몸에서 더 뜨거운 몸으로 열을 전달하는 것은 불가능하다고 말한다.예를 들어, 실온(~72°F) 지역에 뜨거운 커피 한 잔이 있으면 주변으로 열이 전달되어 실내 온도가 약간 상승(~72.3°F)하여 냉각됩니다.그러나, 같은 최초의 커피잔은 주위의 열을 흡수하지 않기 때문에, 실내의 온도가 저하해(최대 71.7°F) 한층 더 뜨거워집니다.따라서 시스템에 추가 에너지가 추가되지 않는 한 커피가 식는 과정은 되돌릴 수 없습니다.

그러나 시스템의 미세 분석과 매크로 상태의 관찰을 조화시키려 할 때 모순이 발생했습니다.많은 과정들이 고전 뉴턴 역학을 사용하여 분석될 때 수학적으로 미시 상태에서 가역적입니다.이 역설은 분자 충돌이 혼합 ^[9]가스의 온도 균등을 수반한다는 제임스 클러크 맥스웰의 1860년 주장과 같이 거시적 평형 경향에 대한 미시적 설명을 명확하게 한다.1872년부터 1875년까지, 루드비히 볼츠만은 볼츠만의 엔트로피 공식의 형태로 이 역설에 대한 통계적 설명을 보강하여, 시스템이 초기 상태로 돌아갈 가능성을 낮추면서, 가능한 미세 상태의 수가 증가한다고 말했다.그의 공식은 다음과 ^[10][11]같이 주장한 제1대 켈빈 남작 윌리엄 톰슨의 분석을 정량화했다.

추상 역학에서 운동 방정식은 완벽하게 가역적입니다; 이러한 방정식의 해는 시간 변수 t가 –t로 대체될 때 유효합니다.반면 물리적 과정은 되돌릴 수 없습니다. 예를 들어 고체의 마찰, 열 전도 및 확산입니다.그럼에도 불구하고, 에너지 소산의 원리는 각 입자가 추상 역학의 법칙에 따르는 분자 이론과 양립할 수 있다.

프랑스 수학자 앙리 푸앵카레가 불가역적 체계에 대한 또 다른 설명을 내놓았다.1890년, 그는 카오스 이론이라고도 불리는 비선형 역학에 대한 첫 번째 설명을 발표했습니다.카오스 이론을 열역학 제2법칙에 적용하면, 불가역성의 역설은 미시 상태에서 거시 상태로의 스케일링과 관련된 오류와 실험 관찰을 할 때 사용되는 자유도에서 설명될 수 있다.관찰 가능한 물리적 ^[12]영역 내에서 돌이킬 수 없는 특성의 전시로 가는 미세 상태 화합물에서의 시스템 및 그 환경과 관련된 초기 조건에 대한 민감도.

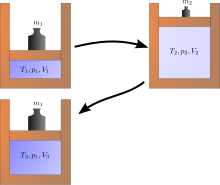
돌이킬 수 없는 프로세스의 예

물리적 영역에는 에너지 전달에서 100% 효율을 달성할 수 없는 돌이킬 수 없는 많은 프로세스가 존재합니다.다음은 프로세스의 ^[13]불가역성에 기여하는 자발적 사건의 목록입니다.

• 노화(이 주장은 논란의 여지가 있다. ^[14]생쥐에서 노화가 역전된다는 것이 입증되었기 때문이다.NAD+^[15]와 텔로머라아제^[16] 또한 노화를 역행하는 것으로 입증되었다.)
• 죽음.
• 시간을
• 한정된 온도차를 통한 열전달
• 마찰
• 소성 변형
• 저항을 통한 전류 흐름
• 히스테리시스에 의한 자화 또는 편파
• 유체의 무제한 팽창
• 자연 화학 반응
• 다양한 조성/상태의 물질의 자발적 혼합

줄팽창은 엔트로피의 증가를 쉽게 계산할 수 있기 때문에 고전적인 열역학의 한 예입니다.이 현상은 용기의 다른 한쪽이 대피한 상태에서 (작은 칸막이를 통해) 열로 격리된 용기의 한쪽에 가스가 보관되는 경우에 발생합니다. 그런 다음 용기의 두 부분 사이의 칸막이가 열리고 가스가 용기 전체를 채웁니다.가스의 내부 에너지는 부피가 증가하는 동안 그대로 유지됩니다.기체를 원래 부피로 압축하는 것만으로는 원래 상태를 복구할 수 없습니다. 왜냐하면 이 압축에 의해 내부 에너지가 증가하기 때문입니다.원래 상태는 재압축된 시스템을 냉각하여 환경을 되돌릴 수 없는 상태로 가열해야만 복구할 수 있습니다.오른쪽 그림은 첫 번째 팽창이 "자유"(줄 팽창)인 경우에만 적용됩니다. 즉, 실린더 외부에 기압이 없고 중량이 상승되지 않을 수 있습니다.

복잡한 시스템

돌이킬 수 있는 사건과 돌이킬 수 없는 사건의 차이는 복잡한 시스템(생체 또는 생태계 등)에서 특별한 설명적 가치가 있다.생물학자 훔베르토 마투라나와 프란시스코 바렐라에 따르면, 살아있는 유기체는 그들의 지속적인 존재를 가능하게 하는 자동이식에 의해 특징지어진다.물리학자이자 화학자인 일리야 프리고긴은 보다 원시적인 형태의 자기 조직 체계를 설명했습니다.복잡한 시스템의 맥락에서, 죽음, 종의 멸종 또는 기상 시스템의 붕괴와 같은 특정 자기 조직 과정의 종말을 초래하는 사건들은 돌이킬 수 없는 것으로 간주될 수 있다.같은 조직원리(예를 들어 동일한 DNA 구조)를 가진 클론이 개발될 수 있다고 해도, 이것은 이전의 별개의 시스템이 다시 태어난다는 것을 의미하지는 않는다.경미한 부상이나 물리적 환경의 변화와 같이 유기체, 종 또는 기타 복잡한 시스템의 자기 조직적 능력이 적응할 수 있는 사건은 되돌릴 수 있다.그러나 적응은 유기체에 대한 네겐트로피의 수입에 따라 달라지며,^[17] 따라서 환경에서 돌이킬 수 없는 과정을 증가시킨다.지속가능성 및 예방원칙과 같은 생태학적 원칙은 ^{[18][19][20][21][22][23][5][24][25]}가역성의 개념을 참고하여 정의할 수 있다.

「 」를 참조해 주세요.

• 엔트로피 생성
• 엔트로피(시간의 화살표)
• 엑서지
• 가역 프로세스(열역학)
• 단방향 함수
• 비균형 열역학
• 대칭 파괴

레퍼런스