모노이드

마그마와 그룹 사이의 대수 구조.예를 들어, 모노이드는 동일성을 가진 반군이다.

수학의 한 분야인 추상대수에서, 모노이드는 연관 2진수 연산과 항등원소를 갖춘 집합이다.예를 들어, 덧셈을 수반하는 음이 아닌 정수는 모노이드를 형성하고, 항등원소는 0이다.

모노이드는 동일성을 가진 반군이다.그러한 대수적 구조는 수학의 여러 분야에서 발생한다.

집합에서 그 자체로 함수는 함수 구성에 관해 모노이드를 형성합니다.보다 일반적으로 범주 이론에서, 물체의 형태 자체는 모노이드를 형성하고, 반대로, 모노이드는 단일 물체를 가진 범주로 볼 수 있다.

컴퓨터 과학과 컴퓨터 프로그래밍에서, 주어진 문자 집합에서 만들어진 문자열 집합은 자유 모노이드입니다.전이 모노이드와 구문 모노이드는 유한 상태 기계를 설명하는 데 사용됩니다.트레이스 모노이드와 이력 모노이드는 프로세스 계산과 동시 컴퓨팅의 기반이 됩니다.

이론 컴퓨터 과학에서 모노이드의 연구는 오토마타 이론(Krohn-Rhodes 이론)과 형식 언어 이론(별 높이 문제)의 기초이다.

피사체의 역사 및 기타 모노이드의 일반적인 특성에 대해서는 반군을 참조하십시오.

정의.

이항 $연산$ S × $S$ → $S$ 를 갖춘 집합 S는 다음 두 공리를 만족하는 경우 모노이드이다.

연관성: S의 모든 a, b 및 c에 대해, $(a$ • $b)$ • $c$ $=$ a • ( $b$ • c $)$ 가 성립한다.
아이덴티티 요소: S의 모든 요소 a에 대해 e • $a$ = $a$ $및$ a • $e$ = $hold$ 라는 $방정식$ 이 존재하도록 S에 요소 e가 존재한다.

즉, 모노이드는 항등원소를 가진 반군이다.그것은 또한 연관성과 정체성을 가진 마그마로 생각될 수 있다.모노이드의 아이덴티티 요소는 ^[1]유일합니다.이러한 이유로 동일성은 상수, 즉 0-ary(또는 무효) 연산으로 간주됩니다.따라서 모노이드는 트리플(S, •, e)의 사양에 따라 특징지어진다.

문맥에 따라서는 2진수 연산을 위한 기호를 생략하여 연산을 병렬 배치로 나타낼 수 있다. 예를 들어 모노이드 공리는 ( $ab) c$ $= a$ ( $bc)$ $및$ ea = $ae$ = a로 쓸 수 있다.이 표기법은 숫자가 곱되는 것을 의미하는 것은 아닙니다.

각 원소가 역수를 갖는 모노이드는 군이다.

모노이드 구조

서브모노이드

모노이드 $(M, •)$ 의 서브모노이드는 모노이드 연산 하에서 닫힌 M의 서브셋 N으로,^[2]^[3] M의 항등원소 e를 포함한다.기호적으로 N이 N $m$ $M이면$ $N,$ $x$ • y $in$ N이면 N은 M의 서브모노이드가 된다.

한편, N이 모노이드 연산 하에서 닫힌 모노이드의 서브셋이며, 이 유전된 연산을 위한 모노이드라면, N은 항일 수 있으므로 반드시 서브모노이드는 아니다.예를 들어, 싱글톤집합 { $0}$ 은 곱셈 하에서 닫히며, 음이 아닌 정수의 (곱셈) 모노이드의 서브모노이드가 아니다.

제너레이터

M의 서브셋 S는 S를 포함한 M의 최소 서브모노이드가 M이면 M을 발생시킨다고 한다.M을 생성하는 유한 집합이 있으면 M은 완전히 생성된 모노이드라고 한다.

가환성 모노이드

연산이 교환적인 모노이드는 교환 모노이드(또는 덜 일반적으로는 아벨 모노이드)라고 불린다.가환성 모노이드는 종종 부가적으로 쓰여진다.어떤 교환 모노이드는 x + $z$ = ^[4] $y$ 와 $같은$ z가 존재한다면 x $y$ y에 $의해$ 정의되는 대수적 사전 순서δ를 부여받는다.교환 모노이드 M의 순서 단위는 M의 원소 u이며, M의 임의의 원소 x에 대하여 $u$ 가 생성하는 집합 내에 x ≤ $v$ 가 존재하도록 한다.이것은 종종 M이 부분 순서 아벨 군 G의 양의 원뿔이고, 이 경우 u는 G의 순서 단위라고 말할 때 사용된다.

부분 치환 모노이드

연산이 일부에 대해 가환성이지만 모든 요소가 미량 모노이드는 아니다.미량 모노이드는 일반적으로 동시 계산 이론에서 발생한다.

예

16개의 가능한 바이너리 부울 연산자 중 양면 정체성을 갖는 4개의 각각은 가환 및 연관성이 있으므로 집합 {False, True}은 가환 모노이드가 됩니다.표준 정의에서는 AND와 XNOR의 ID가 True이고 XOR과 OR의 ID가 False입니다.AND 및 OR의 모노이드도 유용하지만 XOR 및 XNOR의 모노이드도 유용하지 않습니다.
$\mathbb {N} =\{0,1,2,\ldots \}$ N $\mathbb {N} =\{0,1,2,\ldots \}$ { $\mathbb {N} =\{0,1,2,\ldots \}$ , $\mathbb {N} =\{0,1,2,\ldots \}$ , 2 $\mathbb {N} =\{0,1,2,\ldots \}$ , ... $\mathbb {N} =\{0,1,2,\ldots \}$ } { $displaystyle \mathbb {$ N} $=$ \ { $0$ , 1, 2, \ldots $\mathbb {N} =\{0,1,2,\ldots \}$ $\}$ 세트는 덧셈(소수 요소 0) 또는 곱셈(소수 요소 1) 아래의 교환 모노이드입니다.부가되는 $N$ 의 서브모노이드는 수치모노이드라고 불린다.
양의 $\mathbb {N} \setminus \{0\}$ N $\mathbb {N} \setminus \{0\}$ { $}({displaystyle \mathbb$ {N} \ $setminus$ \{ $0\})$ 의 $\mathbb {N} \setminus \{0\}$ 집합은 곱셈(식별 요소 1) 하의 교환 모노이드이다.
$집합$ A가 주어졌을 때, A의 $부분$ 집합은 교차점 아래의 교환 모노이드이다(정체 요소는 A $자체$ 이다).
$집합$ A가 주어졌을 때, A의 $서브셋$ 세트는 합집합 아래의 교환 모노이드입니다(아이덴티티 요소는 빈 집합입니다).
앞의 예제를 일반화하면, 모든 경계 반격자는 공역가환모노이드이다.
- 특히, 임의의 유계 격자는 미트모노이드 구조 및 결합모노이드 구조를 모두 가질 수 있다.아이덴티티 요소는 각각 격자의 맨 위 및 맨 아래입니다.격자로써 헤이팅 대수와 부울 대수는 이러한 모노이드 구조를 타고났다.
이진 연산으로 닫힌 모든 싱글톤집합 { $x}$ 은 • 사소한 (하나의 요소) 모노이드를 형성하며, 이 또한 사소한 그룹입니다.
모든 그룹은 모노이드이고 모든 아벨 그룹은 교환 모노이드이다.
모든 반그룹S는 $단순히$ S에 $속하지$ 않는 $요소$ e에 인접하고 모든 s $µ$ S에 대해 e • $s$ = $s$ • e를 $정의함$ 으로써 $모노이드로$ 변할 수 있다.어떤 반군이든 모노이드로의 변환은 반군의 범주와 ^[5]모노이드의 범주 사이의 자유 함수자에 의해 이루어집니다.
- 따라서 등가성 모노이드(때로는 find-first라고도 함)는 $집합$ S에 걸쳐 왼쪽 0 반군에 대한 항등성 요소 $e$ 에 인접하여 형성될 수 있다.반대편 모노이드(find-last라고도 함)는 S $위$ 의 오른쪽 0 반군에서 형성됩니다.
  - 두 요소 ${lt,$ gt}을(를) 사용하여 왼쪽 0의 반그룹에 $아이덴티티$ e를 인접시킵니다.그 후, 그 결과 도출된 등가 모노이드 ${lt, e,$ gt}는 요소의 순서가 주어진 시퀀스의 사전적 순서를 모델화하며, e는 동등함을 나타낸다.
동작으로서 덧셈 또는 곱셈을 포함한 임의의 링의 기본 세트.(정의상 링은 곱셈 아이덴티티 1을 가집니다).
- 정수, 유리수, 실수 또는 복소수, 덧셈 또는 곱셈을 ^[6]연산으로 합니다.
- 행렬 덧셈 또는 행렬 곱셈을 연산으로 하는 특정 링 위의 모든 nxn 행렬 집합입니다.
일부 고정 알파벳 $δ$ 위의 모든 유한 문자열 집합은 문자열 연결을 연산으로 하는 모노이드를 형성합니다.빈 문자열은 ID 요소로 기능합니다.이 모노이드는 $δ$ 로^∗ 표시되며 $δ$ 위의 유리 모노이드라고 불린다. $δ$ 에 적어도2개의 요소가 있는 경우는 가환되지 않습니다.
임의의 $모노이드$ M이 주어졌을 때, 반대편 $모노이드 op$ M은 M과 $동일$ 한 캐리어 세트 및 동일 요소를 가지며, 그 연산은 $op$ x • $y$ $= y$ • $x$ 로 정의된다. 임의의 교환 모노이드는 그 자체의 반대 모노이드이다.
모노이드 구조(또는 일반적으로 유한한 수의 모노이드, $M 1, ...,$ $M k)$ 를 부여받은 두 $세트$ M 및 $N$ 이 주어졌을 때, 이들의 데카르트 곱 $M$ × $N$ 도 모노이드이다(각각 $M 1$ × δ × $M k$ ).관련 조작과 ID 요소는 쌍으로 ^[7]정의됩니다.
$모노이드$ M을 고정합니다.주어진 집합에서 $M$ 까지의 모든 함수의 집합도 모노이드입니다.identity 요소는 임의의 값을 $M$ 의 ID에 매핑하는 상수 함수입니다.관련 연산은 포인트 단위로 정의됩니다.
연산• 및 항등 $요소$ e로 $모노이드$ M을 고정하고, $M$ 의 모든 서브셋으로 구성된 $멱집합 P ($ M)를 고려한다. 이러한 서브셋에 대한 이진 $연산$ 은S • T $=$ { $s$ : s $s$ S, $t$ t T $}$ 로 정의할 수 있다.그러면 P $(M)$ 가 ID 요소가 ${e}$ 인 모노이드로 $바뀝니다$ .마찬가지로 $그룹$ G의 멱집합은 그룹 서브셋의 곱 아래 모노이드이다.
S를 세트로 $하자$ .모든 $함수$ S → $S$ 의 집합은 함수 구성 하에서 모노이드를 형성한다.아이덴티티는 아이덴티티 함수일 뿐입니다.이것은 $또한$ S의 완전 변환 모노이드라고도 불린다. $만약$ S가 n개의 원소로 $유한$ 하다면, S $위$ 의 함수의 모노이드는 n개의 원소로 $유한$ 하다ⁿ.
위의 예를 일반화하면 C를 카테고리, $X$ 를 $C$ 의 오브젝트로 $합니다$ .끝 $(X)$ 으로 $표기$ 된_C $X$ 의 모든 내형성 집합은 형태론의 구성 아래 모노이드를 형성한다.범주 이론과 모노이드 사이의 관계에 대한 자세한 내용은 아래를 참조하십시오.
연결된 합계가 있는 콤팩트 서페이스의 동형성 클래스 집합입니다.단위 요소는 일반 2-sphere 클래스입니다.또한 a가 토러스 클래스를 나타내고 b가 투영 평면의 클래스를 나타내는 $경우$ , 모노이드의 모든 요소 c는 c $= na$ + $mb$ 형식의 $고유$ 한 식을 갖는다. $여기$ 서 n은 양의 $정수$ 이고 m = $0, 1$ , 또는 $2$ 이다. $3b$ $= a$ + $b$ 입니다.
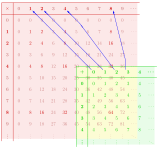
⟨ f 주문 n의 ⟩{\langle f\rangle\displaystyle} 된 순환 monoid, 그것은,⟨ f⟩){f0, f1,…, fn− 1}{\displaystyle\langlef\rangle =\left\{f^{0},f^{1},\dots ,f^{n-1}\right\}}. 그리고 나서 nxfk{\displaystyle f^{n}=f^{k}}0명의≤ k<>에 f, n{\displaystyle 0\leq k<, n}.에서자.사실, $각각$ 의 k는 $n차수$ 의 모노이드를 제공하며, 모든 순환 모노이드는 이들 중 하나와 동형이다.
또한 $f$ 는 다음과 같이 주어진 포인트 $\{0,1,2,\dots ,n-1\}$ { $\{0,1,2,\dots ,n-1\}$ , 2, $\{0,1,2,\dots ,n-1\}$ $\{0,1,2,\dots ,n-1\}$ - $\{0,1,2,\dots ,n-1\}$ }({ $displaystyle$ \{ $0, 1$ , 2 $,\dots$ , $n-1\})$ 에 $\{0,1,2,\dots ,n-1\}$ 대한 함수로 간주할 수 있습니다. $(\displaystyle {bmatrix} 0&1&\cdots &\cdots &\cdots &\cdots &\cdots &\n-1&k\end {bmatrix})$ 또는 동등하게 $f(i):=param{case}i+1,&{\text{if}}0\leq i<n-1\k,&{\text{if}i=n-1.\end {case}$ $\langle f\rangle$ 으로 § f ${\$ { $displaystyle \langle$ f $\rangle }$ 요소의 $\langle f\rangle$ 곱셈을 함수 구성에 의해 구한다.
k $k=0$ $({displaystyle$ $\{0,1,2,\dots ,n-1\},$ k $=0})$ 인 $k=0$ 경우 $함수$ $\{0,1,2,\dots ,n-1\},$ 는 { $\{0,1,2,\dots ,n-1\},$ , $\{0,1,2,\dots ,n-1\},$ , $\{0,1,2,\dots ,n-1\},$ n - $},$ ${{0, 1$ , $2,\displaystyle$ , $n-1\}$ 의 $\{0,1,2,\dots ,n-1\},$ 순열이며 $고유$ 한 순서 n의 순환 그룹을 제공합니다.

특성.

모노이드 공리는 e와 $f$ 가 모노이드의 동일 $요소$ 라면 $e$ = $ef$ = $f$ 라는 동일 $요소$ e가 유일하다는 것을 의미한다.

제품과 파워

각 음이 $아닌$ 정수 n에 대해 $pn =$ $p_{n}=\textstyle \prod _{i=1}^{n}a_{i}$ i $p_{n}=\textstyle \prod _{i=1}^{n}a_{i}$ $p_{n}=\textstyle \prod _{i=1}^{n}a_{i}$ $p_{n}=\textstyle \prod _{i=1}^{n}a_{i}$ a {\ $displaystyle p_{n}$ = \ $textstyle \textstyle$ $(a_{1},\ldots ,a_{n})$ ${i=1}^{n_i}$ a_{i $p_{n}=\textstyle \prod _{i=1}^{n}a_{i}$ } }의 $임의$ 의 $(a_{1},\ldots ,a_{n})$ 배열(1 $(a_{1},\ldots ,a_{n})$ $(a_{1},\ldots ,a_{n})$ $)$ { $displaystyle (a_{1$ },\ $ldots, a_{$ n $}$ n} n} n} n의 n의 n의 n의 n의 n의 n의 n의 n의 n의 n의 n의 n의 n의 n의 $p_{n}=\textstyle \prod _{i=1}^{n}a_{i}$ 을 재귀적으로 $정의$ 할₀ 수 있다.

특별한 경우로서 n ≤ $1$ 에 $대해$ monoid 원소 $x$ 의 비음정 정수승 $x 0$ = $1$ $및 n$ x $= x n -1$ • $x$ 를 정의할 수 있다. $그러면 m + n$ x $= x m$ • $모든 n$ m, n $0$ 0에 대해 x가 됩니다.

반전 요소

$요소$ $x$ 는 $x$ • $y$ = $e$ 및 $y$ • x = e인 $요소$ y가 존재하는 경우 가역이라고 합니다. $요소$ y는 $x$ 의 역수라고 불립니다.역수가 존재할 경우 다음과 같이 고유합니다. $y$ 와 z가 $x$ 의 역수인 $경우$ , y = ey $=$ ( $zx) y$ $= ze$ =^[8] ze = $z$ .

예를 들어, $역y$ 를 사용하여 x가 반전할 수 $있는$ $경우$ , $각$ n ; $1$ 에⁻ⁿ $대해 n$ x = y를 설정하여 $x$ 의 음의 거듭제곱을 정의할 수 있습니다. 이렇게 하면 $모든 m$ , n $z$ Z에 $대해 m + n$ $x m$ = $x n$ • x가 유지됩니다.

조작 •과 함께 모노이드의 모든 반전 요소 집합이 그룹을 형성합니다.

그로텐디크 군

모든 모노이드가 그룹 안에 있는 것은 아닙니다.예를 들어 b가 항등원소가 $아니더라도$ a • $b$ = $a$ 가 $유지$ 되도록 2개의 $원소$ a 및 $b$ 가 존재하는 모노이드를 갖는 것이 완벽하게 가능하다.이러한 모노이드는 그룹에 포함될 수 없다. 왜냐하면 $양쪽$ 을 a의 $역수$ 로 곱하면 b = $e$ 를 얻을 수 있기 때문인데, 이는 사실이 아니다.

모노이드 $(M, •)$ 는 M의 $모든$ a, $b$ $및$ c에 대해 $등식$ a $= a$ • $c$ 가 b = $c$ 를 $의미$ 하고 $등식$ b $= c$ • $a$ = $c$ 가 b = $c$ 를 $의미$ 할 경우 소거 특성을 가진다(또는 소거).

소거성을 가진 교환모노이드는 그로텐디크군 구성을 통해 항상 그룹에 삽입할 수 있다.이것이 정수의 가법군(연산 +를 갖는 군)이 자연수의 가법 모노이드(연산 +와 소거 특성을 갖는 가법 모노이드)로부터 구성되는 방법이다.단, 비가환적 취소 모노이드를 그룹에 포함할 필요는 없습니다.

만약 모노이드가 소거 특성을 가지고 유한하다면, 그것은 사실상 ^[9]군이다.

모노이드의 오른쪽 및 왼쪽 취소 요소는 차례로 하위 모노이드를 형성한다(즉, 연산 하에서 닫히고 분명히 동일성을 포함한다).즉, 모든 교환 모노이드의 취소 요소가 그룹으로 확장될 수 있습니다.

모노이드의 취소 특성은 그로텐디크 시공을 수행하기 위해 필요하지 않습니다. 정류성은 충분합니다.단, 치환성 모노이드가 소거성을 가지지 않는 경우에는 그로텐디크기로의 모노이드의 동형성은 주입되지 않는다.보다 정확하게는 a • $b$ $= a$ • $c$ 일 $경우$ , $b$ 와 c는 b $µ$ $c일지$ 라도 그로텐디크 그룹에서 동일한 이미지를 $가진다$ .특히, 만약 모노이드가 흡수 원소를 가지고 있다면, 그 그로텐디크 그룹은 사소한 군이다.

모노이드의 종류

역모노이드는 M의 모든 a에 대해 m에 고유한⁻¹ a가 존재하여 $a -1$ = $a -1$ • a • $a -1$ 및 $a$ = $a$ • $a -1$ • a • a가 $존재$ 하는 모노이드이다. 역모노이드가 소거식이면 군이다.

$반대$ 로, 제로섬프리 모노이드는 a + $b$ = 0이 $a$ = 0 $및$ $b$ =^[10] 0: 등가성을 $의미$ 하며, 0 이외의 어떤 원소도 가법 반전을 가지지 않는 것을 의미하는 가법이다.

작용 및 연산자 모노이드

M을 모노이드로 하고, 2진 연산을 •로 나타내며, 항등 요소를 e로 나타내자.(왼쪽) M-act(또는 M 위의 왼쪽 작용)는 다음과 같이 모노이드 구조와 양립 가능한 연산 $θ :$ M × $X$ → $X$ 와 함께 집합 X이다.

모든 x in X: e $µ$ $x$ = $x$ ;
모든 a, b in M 및 x in X: $a$ µ ( $b µ$ x)= ( $a$ • $b) µ$ x.

이것은 (왼쪽) 집단 행동의 모노이드 이론과 유사하다.오른쪽 M-act도 비슷한 방식으로 정의됩니다.작용이 있는 모노이드는 연산자 모노이드로도 알려져 있습니다.중요한 예로는 반자동 천이계를 들 수 있다.변환반군은 항등변환에 인접함으로써 연산자 모노이드로 할 수 있다.

모노이드 동형사상

(

N, +, 0)

부터

(N, \times, 1

)까지의 모노이드 동형

x 2 x

2의 예.그것은 주입적이긴 하지만, 돌출적이지는 않다.

두 모노이드 $(M,$ θ)와 ( $N, •)$ 사이의 동형성은 다음과 같은 $함수 f$ : M → $N$ 이다.

$f (x µ$ y)= $f (x)$ • $f (y)$ (M의 모든 x, y)
$f (e M)$ = $e N$ ,

여기서_M e와_N e는 각각 M과 N의 아이덴티티입니다.모노이드 동형사상은 때때로 단순히 모노이드 형태라고 불린다.

비록 ^[11]동질성이 동질성의 이미지의 동일성일지라도, 그것은 동질성을 대상 모노이드의 동일성에 매핑하지 않을 수 있기 때문에, 모노이드 사이의 모든 반군 동질성이 모노이드의 동일성인 것은 아니다. $M_{n}$ 를 들어 곱셈을 갖춘 잔차 클래스 모듈 $n$ 의 $n$ 세트인 $M_{n}$ n { $display$ $style$ M _ { $n$ } 。특히 $1$ 의 $1$ 가 $아이덴티티입니다$ $f\colon M_{3}\to M_{6}$ f : M 3 $f(k)=3k$ $f\colon M_{3}\to M_{6}$ $f\colon M_{3}\to M_{6}$ ( k ) $f\colon M_{3}\to M_{6}$ $f(k)=3k$ $f(k)=3k$ $f(k)=3k$ ( $f(k)=3k$ ) $= 3$ k ( k ) $f(k)=3k$ $3$ $3k\cdot 3l=9kl=3kl$ $3k\cdot 3l=9kl=3kl$ 3 l $3k\cdot 3l=9kl=3kl$ $3k\cdot 3l=9kl=3kl$ $3k\cdot 3l=9kl=3kl$ $3k\cdot 3l=9kl=3kl$ $3k\cdot 3l=9kl=3kl$ $3k\cdot 3l=9kl=3kl$ $3k\cdot 3l=9kl=3kl$ ( \ $display style$ $3$ $3k\cdot 3l=9kl=3kl$ k \ $cd$ 3 l = 3 $3k\cdot 3l=9kl=3kl$ ( \ $3k\cdot 3l=9kl=3kl$ display 3 k \ cd 3 l ) $f\colon M_{3}\to M_{6}$ $=$ 3 k ( \ $M_{6}$ 6 $)$ 의 반군 $f\colon M_{3}\to M_{6}$ $3k\cdot 3l=9kl=3kl$ $M_{6}$ 이다.동형사상은 첫 번째 모노이드의 동일성과 두 번째 모노이드의 동일성을 매핑하는 모노이드 사이의 반군 동형사상이며, 후자의 조건은 생략될 수 없다.

대조적으로, 그룹들 사이의 반군 동형사상은 항상 군 동형사상이며, 이는 반드시 동형을 보존하기 때문이다. (왜냐하면, 그룹에서, 동형은 x $µ$ x = $x$ 와 $같은$ 유일한 요소이기 때문이다.)

비주사적 모노이드 동형사상은 모노이드 동형사상이라고 불린다.두 개의 모노이드는 만약 그들 사이에 모노이드의 동형이 존재한다면 동형이라고 한다.

동등 프레젠테이션

모노이드는 그룹 프레젠테이션을 통해 그룹을 지정할 수 있는 것과 같은 방식으로 프레젠테이션을 제공할 수 있습니다.이를 위해 발생기 세트 δ 및 자유 모노이드 δ^∗ 상의 관계 세트를 지정한다.위와 같이 δ의^∗ 이항 관계를 monoid 합치까지 확장한 다음, comment monoid를 구성함으로써 이것을 할 수 있다.

이항관계 $R$ ⊂× × $σ * σ *$ , , , , , $given -1$ given given r its its its its its its its its its its its its $its$ closure closure이것은 ( $u, v) r$ R $r -1$ R인 일부 $문자열$ $u$ , $v,$ $s,$ $t$ ∈ $σ *$ σ r r R에 $E 대해$ x = $sut$ $및$ y = $svt$ 를 $정의함$ 으로써 대칭 관계E × $σ *$ σ σ $σ *$ σ σ σ σ σ σ σ σ a a by if if if if if if if if if if if if if if if if if if if and and and and and and and and and and and and

일반적인 상황에서는 R $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ { $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ 1 $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ 1 , $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ , $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ n $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ { $displaystyle$ R = \ { $u$ _ {1 $} = v _$ { n } \ $cdots$ , $u _$ { n } = v $_$ { $n$ } \ $R=\{u_{1}=v_{1},\cdots ,u_{n}=v_{n}\}$ } 。예를 들어,

\displaystyle \p,q,\vert \;pq=1\rangle }

이환식 모노이드에 대한 등식 표현이다.

(\displaystyle \brantle a,b,\vert \;aba=ba,bba=bab\rangle }

는 도수 2의 플라스틱 모노이드입니다(무한 차수를 가집니다).이 플라스틱 모노이드의 요소는 $a^{i}b^{j}(ba)^{k}$ $a^{i}b^{j}(ba)^{k}$ ( $a^{i}b^{j}(ba)^{k}$ a ) $a^{i}b^{j}(ba)^{k}$ \ $displaystyle$ a $^{i}b^{j}($ ba $)$ 로 표기할 수 있다. $^{k}:$ 정수 $a^{i}b^{j}(ba)^{k}$ i, j, k의 경우 ba가 a와 b 둘 다와 일치함을 알 수 있습니다.

범주론과의 관계

그룹형 구조
	토탈리티^α	연관성	신원	나누기	정류성
반군체	불필요.	필수의	불필요.	불필요.	불필요.
소분류	불필요.	필수의	필수의	불필요.	불필요.
그룹상	불필요.	필수의	필수의	필수의	불필요.
마그마	필수의	불필요.	불필요.	불필요.	불필요.
준군	필수의	불필요.	불필요.	필수의	불필요.
유니탈 마그마	필수의	불필요.	필수의	불필요.	불필요.
세미그룹	필수의	필수의	불필요.	불필요.	불필요.
고리	필수의	불필요.	필수의	필수의	불필요.
모노이드	필수의	필수의	필수의	불필요.	불필요.
그룹.	필수의	필수의	필수의	필수의	불필요.
가환성 모노이드	필수의	필수의	필수의	불필요.	필수의
아벨 군	필수의	필수의	필수의	필수의	필수의
^α 많은 선원에 의해 사용되며 다르게 정의되는 폐쇄 공리는 동등하다.

모노이드는 범주의 특별한 클래스로 볼 수 있습니다.실제로, 모노이드 연산에 필요한 공리는 소스와 대상이 주어진 ^[12]객체인 모든 형태소 집합으로 제한될 때 형태소 구성에 필요한 공리다.그것은,

모노이드는 본질적으로 하나의 물체를 가진 범주와 같은 것입니다.

보다 정확하게는, 모노이드 $(M, •)$ 가 주어졌을 때, 하나의 객체만으로 작은 카테고리를 구성할 수 있으며, 그 모피즘이 M의 요소이다.형태소의 구성은 모노이드 연산에 의해 주어진다. •

마찬가지로, 모노이드 동형사상은 단일 객체 ^[12]범주 사이의 펑터일 뿐입니다.따라서 이 구성은 (작은) 모노이드 Mon의 범주와 (작은) Cat의 범주의 완전한 하위 범주 사이에 동등성을 부여한다.마찬가지로 그룹의 범주는 Cat의 다른 전체 하위 범주와 동일합니다.

이런 의미에서 범주 이론은 모노이드의 개념의 확장으로 생각될 수 있다.모노이드에 대한 많은 정의와 정리는 둘 이상의 객체를 가진 작은 범주로 일반화될 수 있다.예를 들어, 하나의 객체가 있는 범주의 몫은 단지 몫 모노이드에 불과합니다.

다른 대수적 구조들과 마찬가지로, 모노이드도 그들만의 범주인 Mon을 형성하는데, 그 물체는 모노이드이고 그 형태론은 모노이드 ^[12]동형사상입니다.

또한 범주에서 모노이드가 무엇인지에 대한 추상적인 정의인 모노이드의 개념도 있다.세트의 모노이드 객체는 그냥 모노이드입니다.

컴퓨터 공학에서의 모노이드

컴퓨터 과학에서 많은 추상 데이터 유형은 모노이드 구조를 가질 수 있다.공통의 패턴에서는, 모노이드의 일련의 요소를 「접기」또는 「누적」하고, 최종치를 생성한다.예를 들어, 많은 반복 알고리즘은 각 반복마다 일종의 "실행 합계"를 업데이트해야 합니다. 이 패턴은 모노이드 연산에 의해 우아하게 표현될 수 있습니다.또, 복수의 코어 또는 프로세서를 효율적으로 이용하기 위해서, 모노이드 연산의 관련성은, 프리픽스 합계 또는 유사한 알고리즘을 채용하는 것으로, 연산을 병렬화할 수 있는 것을 보증한다.

ID $\varepsilon$ $"\displaystyle \varepsilon"$ 및 $\varepsilon$ 관련 연산 $"\displaystyle \bullet$ 을 가진 유형 M 값 시퀀스를 지정하면 폴드 동작은 다음과 같이 정의됩니다.

\displaystyle \mathrm {fold} : M^{*}\rightarrow M=\ell \mapsto {case}\varepsilon &{\mbox{if}}}\ell =\mathrm {fold}\ell {mathrm},

또한 데이터 구조의 요소를 직렬화하면 모든 데이터 구조를 유사한 방식으로 '접을 수' 있습니다.예를 들어, 이진 트리의 "폴딩" 결과는 사전 순서와 사후 순서 트리 통과에 따라 다를 수 있습니다.

맵 리듀스

컴퓨터 공학에서 모노이드의 적용은 소위 MapReduce 프로그래밍 모델입니다(왼쪽 폴딩으로 Map-Reduce를 모노이드로 인코딩 참조).컴퓨팅에서 MapReduce는 두세 번의 작업으로 구성됩니다.데이터셋을 지정하면 "맵"은 임의의 데이터를 특정 모노이드의 요소에 매핑하는 것으로 구성됩니다."Reduce"는 이러한 요소들을 접는 것으로 구성되며, 결국 우리는 하나의 요소만을 생산합니다.

예를 들어, 멀티셋이 있는 경우, 프로그램에서는 요소에서 숫자로의 맵으로 표시됩니다.이 경우 요소를 키라고 합니다.고유 키의 수가 너무 많을 수 있으며, 이 경우 멀티셋이 샤드됩니다.절감을 올바르게 완료하기 위해 "Shuffling" 단계는 노드 간에 데이터를 다시 그룹화합니다.이 단계가 필요하지 않은 경우, 전체 맵/축소는 매핑과 축소로 구성됩니다. 두 연산 모두 병렬화할 수 있습니다. 전자는 요소별 특성으로 인해, 후자는 모노이드의 연관성으로 인해 가능합니다.

완전 모노이드

완전 모노이드는 다음과 같이^[13]^[14]^[15]^[16] 모든 지수 $집합$ I에 대해 무한합 연산 $\Sigma _{I}$ I(\ $displaystyle \Sigma$ _ ${I})$ 를 $\Sigma _{I}$ 갖춘 교환 모노이드를 말한다.

\sum _{i\in \emptyset }{m_{i}=0;\sum \{j\}{m_{j}=m_{j};\sum \{i\in \j,k\}{m_{i}}=m_{i}}{m_{i}}}{m_{ne}}{j}}}{{\ne}}}}{ne}}}{m_{ne}}}}}}{m_m_m_m_m_{ne}}}}{ne}{ne}{

그리고.

j j

I

{\

text

{

and

}}}

I_

{j

}\cap

I_

{j'}=\emptyset \text{ for

}}

j\neq

j

\sum _{j\in J}{\sum _{i\in I_{j}}{m_{i}}}=\sum _{i\in I}m_{i}\quad {\text{ if }}\bigcup _{j\in J}I_{j}=I{\text{ and }}I_{j}\cap I_{j'}=\emptyset \quad {\text{ for }}j\neq j'

순서 교환성 모노이드는 a θ M마다 a $θ$ 0, a $b$ 는 $a,$ $b$ , c $θ$ M 전체에 $대해$ $a$ + c $θ$ b + $c$ 를 $의미$ 하도록 $부분$ 순서θ와 함께 교환성 $모노이드$ M이다.

연속 모노이드는 순서 있는 교환 모노이드 $(M,$ δ)이며, 여기서 모든 유도 서브셋은 최소 상한을 가지며, 이러한 최소 상한이 모노이드 연산과 호환된다.

a+\sup S=\sup(a+S)

$모든 µ$ M 및 M의 $유도$ $서브셋$ S에 대해.

( $M,$ θ)이 연속 모노이드인 경우, 지수 $집합$ I 및 요소 $집합 i$ a에 $i \in I$ 대해 다음을 정의할 수 있다.

\displaystyle \sum _{I}a_{i}=\sup _{\text{cap}}E\subset I}\;\sum _{E}a_{i}}

$그리고$ M과 이 무한합계 연산은 완전한 ^[16]모노이드가 됩니다.

「」를 참조해 주세요.

메모들

^ e와₂ e가 모두 위의₁ 방정식을 만족한다면 e = e₁ • e₂ = e입니다₁₂.
^ 제이콥슨 2009.
^ 일부 저자는 서브모노이드가 정의에서 반드시 동일성 요소를 포함해야 한다는 요구사항을 생략하고, M과 구별될 수 있는 동일성 요소만을 가져야 한다.
^ Gondran, Michel; Minoux, Michel (2008). Graphs, Dioids and Semirings: New Models and Algorithms. Operations Research/Computer Science Interfaces Series. Vol. 41. Dordrecht: Springer-Verlag. p. 13. ISBN 978-0-387-75450-5. Zbl 1201.16038.
^ 를 클릭합니다Rhodes, John; Steinberg, Benjamin (2009), The q-theory of Finite Semigroups: A New Approach, Springer Monographs in Mathematics, vol. 71, Springer, p. 22, ISBN 9780387097817.
^ Jacobson 2009, 페이지 29, 예 1, 2, 4, 5.
^ 제이콥슨 2009, 페이지 35
^ 제이콥슨, I.5 페이지 22
^ 증명: 모노이드에 x $요소$ 를 고정합니다.모노이드는 유한하기 $때문$ 에ⁿ $,$ $일부$ m > $n$ > 0에 $대해 m$ x = x이다. 그러나 소거에 $의해 m - n$ $x$ = e가 된다. $여기$ 서 e는 항등식이다. $따라서$ x • $x m - n - 1$ = $e$ 이므로 x는 역수를 가집니다.
^ Wehrung, Friedrich (1996). "Tensor products of structures with interpolation". Pacific Journal of Mathematics. 176 (1): 267–285. doi:10.2140/pjm.1996.176.267. Zbl 0865.06010.
^ $f$ $(x)* f (e M)$ = $f (x * e M)$ = f $(x)$ 일 때, f는 반군 $동형사상$ 이고 e는 그 $도메인$ $모노이드 M$ M의 동일성이다.
^ ^a ^b ^c Awodey, Steve (2006). Category Theory. Oxford Logic Guides. Vol. 49. Oxford University Press. p. 10. ISBN 0-19-856861-4. Zbl 1100.18001.
^ Droste, M., & Kuich, W. (2009년)세미링 및 정식 파워 시리즈.가중 오토마타 핸드북, 3-28. doi:10.1007/978-3-642-01492-5_1, 페이지 7-10
^ Hebisch, Udo (1992). "Eine algebraische Theorie unendlicher Summen mit Anwendungen auf Halbgruppen und Halbringe". Bayreuther Mathematische Schriften (in German). 40: 21–152. Zbl 0747.08005.
^ Kuich, Werner (1990). "ω-continuous semirings, algebraic systems and pushdown automata". In Paterson, Michael S. (ed.). Automata, Languages and Programming: 17th International Colloquium, Warwick University, England, July 16-20, 1990, Proceedings. Lecture Notes in Computer Science. Vol. 443. Springer-Verlag. pp. 103–110. ISBN 3-540-52826-1.
^ ^a ^b Kuich, Werner (2011). "Algebraic systems and pushdown automata". In Kuich, Werner (ed.). Algebraic foundations in computer science. Essays dedicated to Symeon Bozapalidis on the occasion of his retirement. Lecture Notes in Computer Science. Vol. 7020. Berlin: Springer-Verlag. pp. 228–256. ISBN 978-3-642-24896-2. Zbl 1251.68135.

레퍼런스

Howie, John M. (1995), Fundamentals of Semigroup Theory, London Mathematical Society Monographs. New Series, vol. 12, Oxford: Clarendon Press, ISBN 0-19-851194-9, Zbl 0835.20077
Jacobson, Nathan (1951), Lectures in Abstract Algebra, vol. I, D. Van Nostrand Company, ISBN 0-387-90122-1
Jacobson, Nathan (2009), Basic algebra, vol. 1 (2nd ed.), Dover, ISBN 978-0-486-47189-1
Kilp, Mati; Knauer, Ulrich; Mikhalev, Alexander V. (2000), Monoids, acts and categories. With applications to wreath products and graphs. A handbook for students and researchers, de Gruyter Expositions in Mathematics, vol. 29, Berlin: Walter de Gruyter, ISBN 3-11-015248-7, Zbl 0945.20036
Lothaire, M. (1997), Combinatorics on words, Encyclopedia of Mathematics and Its Applications, vol. 17, Perrin, D.; Reutenauer, C.; Berstel, J.; Pin, J. E.; Pirillo, G.; Foata, D.; Sakarovitch, J.; Simon, I.; Schützenberger, M. P.; Choffrut, C.; Cori, R.; Lyndon, Roger; Rota, Gian-Carlo. Foreword by Roger Lyndon (2nd ed.), Cambridge University Press, doi:10.1017/CBO9780511566097, ISBN 0-521-59924-5, MR 1475463, Zbl 0874.20040

외부 링크

"Monoid", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. "Monoid". MathWorld.
PlanetMath의 모노이드.

[1] 와₂ e가 모두 위의₁ 방정식을 만족한다면 e = e₁ • e₂ = e입니다₁₂.

[FOOTNOTEJacobson2009-2] 제이콥슨 2009.

[3] 일부 저자는 서브모노이드가 정의에서 반드시 동일성 요소를 포함해야 한다는 요구사항을 생략하고, M과 구별될 수 있는 동일성 요소만을 가져야 한다.

[4] Gondran, Michel; Minoux, Michel (2008). Graphs, Dioids and Semirings: New Models and Algorithms. Operations Research/Computer Science Interfaces Series. Vol. 41. Dordrecht: Springer-Verlag. p. 13. ISBN 978-0-387-75450-5. Zbl 1201.16038.

[5] 를 클릭합니다Rhodes, John; Steinberg, Benjamin (2009), The q-theory of Finite Semigroups: A New Approach, Springer Monographs in Mathematics, vol. 71, Springer, p. 22, ISBN 9780387097817.

[FOOTNOTEJacobson200929,_examples_1,_2,_4_&_5-6] Jacobson 2009, 페이지 29, 예 1, 2, 4, 5.

[FOOTNOTEJacobson200935-7] 제이콥슨 2009, 페이지 35

[8] 제이콥슨, I.5 페이지 22

[9] 증명: 모노이드에 x $요소$ 를 고정합니다.모노이드는 유한하기 $때문$ 에ⁿ $,$ $일부$ m > $n$ > 0에 $대해 m$ x = x이다. 그러나 소거에 $의해 m - n$ $x$ = e가 된다. $여기$ 서 e는 항등식이다. $따라서$ x • $x m - n - 1$ = $e$ 이므로 x는 역수를 가집니다.

[10] Wehrung, Friedrich (1996). "Tensor products of structures with interpolation". Pacific Journal of Mathematics. 176 (1): 267–285. doi:10.2140/pjm.1996.176.267. Zbl 0865.06010.

[11] $f$ $(x)* f (e M)$ = $f (x * e M)$ = f $(x)$ 일 때, f는 반군 $동형사상$ 이고 e는 그 $도메인$ $모노이드 M$ M의 동일성이다.

[Awo10-12] Awodey, Steve (2006). Category Theory. Oxford Logic Guides. Vol. 49. Oxford University Press. p. 10. ISBN 0-19-856861-4. Zbl 1100.18001.

[droste-13] Droste, M., & Kuich, W. (2009년)세미링 및 정식 파워 시리즈.가중 오토마타 핸드북, 3-28. doi:10.1007/978-3-642-01492-5_1, 페이지 7-10

[14] Hebisch, Udo (1992). "Eine algebraische Theorie unendlicher Summen mit Anwendungen auf Halbgruppen und Halbringe". Bayreuther Mathematische Schriften (in German). 40: 21–152. Zbl 0747.08005.

[15] Kuich, Werner (1990). "ω-continuous semirings, algebraic systems and pushdown automata". In Paterson, Michael S. (ed.). Automata, Languages and Programming: 17th International Colloquium, Warwick University, England, July 16-20, 1990, Proceedings. Lecture Notes in Computer Science. Vol. 443. Springer-Verlag. pp. 103–110. ISBN 3-540-52826-1.

[Kuich11-16] Kuich, Werner (2011). "Algebraic systems and pushdown automata". In Kuich, Werner (ed.). Algebraic foundations in computer science. Essays dedicated to Symeon Bozapalidis on the occasion of his retirement. Lecture Notes in Computer Science. Vol. 7020. Berlin: Springer-Verlag. pp. 228–256. ISBN 978-3-642-24896-2. Zbl 1251.68135.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

α

[12]

[13]

[14]

[15]

[16]

Search

모노이드

네임스페이스

더

목차

정의.