호프 대수

수학에서 하인츠 홉프의 이름을 딴 홉프 대수학은 (유니탈 연상) 대수학과 (유니탈 연합) 합금브라라는 동시에 이 구조물의 호환성이 바이알지브라로 되어 있고, 게다가 그 구조에는 일정한 성질을 만족시키는 반유동체주의가 갖추어져 있다. Hopf 대수학의 표현 이론은 특히 좋은데, 이는 호환되는 결합, 상담, 대척점의 존재는 표현, 사소한 표현, 이중표현의 텐서 생산물을 만들 수 있기 때문이다.

홉프 알헤브라는 아마도 가장 친숙한 바이알게브라 타입이 될 것이다. 홉프 알헤브라는 또한 그들 나름대로 연구되고 있는데, 한편으로는 구체적인 종류의 예에 대한 많은 연구와 다른 한편으로는 분류 문제에 대한 연구도 있다. 그들은 응축 물질 물리학과 양자장 이론에서부터^[1] 끈 이론과^[2] LHC 현상학에 이르기까지 다양한 응용 분야를 가지고 있다.^[3]

형식 정의

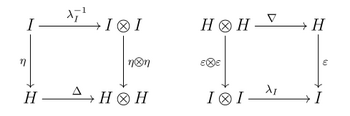
형식적으로, 호프 대수학(Hopf 대수학)은 K-선형 지도 S: H → H (대항선이라고 함)와 함께 필드 K 위에 있는 (연관 및 공동 연관) 바이알게브라 H로, 다음과 같은 도표가 통용된다.

여기서 Δ는 바이알게브라, 그 곱셈, 단위, 카운슬링을 합한 것이다. sumless sweedler 표기법에서 이 속성은 또한 다음과 같이 표현될 수 있다.

${\displaystyle S(c_{(1)}}c_{(2)=c_{(1)S(c_{(2)}=\varepsilon(c)1\qquad {\mbox{모든 }}$

알헤브라의 경우, 위 정의에서 밑부분의 K장을 정류 링 R로 대체할 수 있다.^[4]

Hopf 대수학의 정의는 자기 이중(위 도표의 대칭에 반영됨)이기 때문에 H의 이중(H가 유한한 차원일 경우 항상 가능한 것)을 정의할 수 있다면 자동으로 Hopf 대수학이다.^[5]

구조물 상수

기본 벡터 공간에 대한$$ 기준${\displaystyle }${${\displaystyle {ek}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \{e_{k}\}}}$을(를) 수정하면 다음과 같이 곱셈을 위한 구조 상수의 관점에서 대수학을 정의할 수 있다.

${\displaystyle e_{i}\desla e_{j}=\sum _{k}\mu_{\;ij}^{k}e_{k}}}}}}}$

공동 곱하기:

${\displaystyle \Delta e_{i}=\sum _{j,k}\nu_{i}^{{i}^{\j}e_{j}\otimes e_{k}}}}}}}$

대척점:

${\displaystyle Se_{i}=\sum _{j}\tau _{i}^{\;j}e_{j}}}}}$

연관성은 다음 사항을 요구한다.

${\displaystyle \mu_{\;ij}^{k}^{k}\mu_{\n}^{k}\m}}$

그러나 공동연대는 그것을 필요로 한다.

${\displaystyle \nu \{k}^{{k}^{\;ij}\nu _{i}^{nj}}}$

연결 공리에는 다음이 필요하다.

${\displaystyle \nu \{k}^{{k}^{\\;ij}\tau _{j}^{j}^{n}=\nu _{k}^{k}^{n}}\i}\i}\mau _{j}^{\;pm}^{n}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

대격막의 특성

대척점 S는 때때로 유한차원 사례에서 자동인^{[clarification needed]} K-선형 역이 필요하거나, H가 정류형 또는 코코뮤트(또는 보다 일반적으로 quasitriangular)인 경우 필요하다.

일반적으로 S는 반호모형이기 때문에 ^[6]S는² 동형상이며, 따라서 S가 (필요할 수 있는 대로) 변환불가능하면 자동형상이다.

S² = id일_H 경우, Hopf 대수학은 비자발적이라고 한다(그리고 비자발적인 기본 대수학은 *-알지브라임). H가 특성 0, 교호작용 또는 코콤무트의 영역에 대해 유한차원 반시 구현된 경우, 비자발적이다.

만약 Bialgebra B가 대척점 S를 인정한다면, S는 독특하다("Bialgebra는 최대 1 Hopf 대수 구조를 인정한다").^[7] 따라서, 대척점은 우리가 선택할 수 있는 추가적인 구조를 제공하지 않는다. 홉프 대수학자가 되는 것은 바이알지브라(Bialgebra)의 속성이다.

대척점은 g를 g로⁻¹ 보내는 그룹의 반전 맵과 유사하다.^[8]

호프 아발게브라질

Hopf 대수학 H의 하위골격 A는 H의 하위골격이고 대척 S가 A를 A로 매핑하는 경우 Hopf 하위골격이다. 즉, H의 곱셈, 곱셈, 곱셈, 카운티, 대척점이 A로 제한될 때(추가적으로 H의 아이덴티티 1이 A에 있어야 하는 경우) 그 자체로 Hopf 대수인 것이다. 니콜스-조엘러 자유도 정리는 (1989년) H가 유한한 차원일 경우 자연 A-모듈 H가 유한한 등급이 없다는 것을 확립했다. 즉, 하위그룹에 대한 라그랑주의 정리의 일반화. 이것과 적분 이론의 핵심으로서, 유한 차원 Hopf 대수학의 Hopf 하위 골격은 자동으로 반실행된다.

만약 그것이 adr(h)(A)⊆ 모든 hH, 어디에서 딱 들어맞는?수반 매핑 adr adr(h)(를))S(h(1))ah(2)에 의해 모두 A, H에 h마찬가지로, 일반적인 H에 남아 있는 호프 subalgebra에 왼쪽 수반 매핑에서 안정적은 사양에 정의된에서 a로 정의된 안정의 조건에 맞는으로 알려진 한 호프 subalgebra 호프 대수 H에 정상이 될dl(h)(를)) has₍₁₎(h₍₂₎) 정격성의 두 조건은 항정신대 S가 비주사적인 경우 등가인데, 이 경우 A는 정상적인 Hopf 하위격자라고 한다.

H의 정상적인 Hopf 하위골격 A는 (H의 하위골격의 동일성) 조건을 만족시킨다. HA⁺ = AH는⁺⁺ K에 대한 상담의 커널을 나타낸다. 이 정규성 조건은 HA가⁺ H의 Hopf 이상(즉, 카운티의 커널에서 대수적 이상, 대척점 아래에서 공동체의 안정적)임을 의미한다. 그 결과 홉프 대수 H/HA와⁺ 인식론 H → H/AH가⁺ 있는데, 이는 집단 이론에서 정상 부분군 및 지수 집단의 그것과 유사한 이론이다.^[9]

호프 주문

분수 K 필드가 있는 적분 영역 R에 대한 Hopf 주문 O는 대수 및 합금자리 연산에 따라 닫히는 K에 대한 Hopf 대수 H의 주문이다. 특히, 복합복제 Δ는 O에서 O까지 매핑한다.^[10]

그룹 유사 요소

그룹과 같은 원소는 Δ(x) = x⊗x와 같은 0이 아닌 원소 x이다. 그룹과 같은 원소는 대척점에 의해 주어진 역순으로 그룹을 형성한다.^[11] 원시 원소 x는 Δ(x) = x⊗1 + 1⊗x를 만족한다.^[12][13]

예

	에 따라	콤멀티제이션	상담	대척점	정류적	코코메토티브	언급
집단 대수학 KG	무리를 짓다 G	Δ(g) = G의 모든 G에 대해 g ⊗ g	ε(g) = 모든 G in G에 대한 1	S(g) = 모든 G in G에 대한−1 g	만약 G가 아벨리안이라면	네
함수[14] f 유한 그룹에서 K, KG(점 추가 및 곱셈 포함)까지	유한군 G	Δ(f)(x,y) = f(xy)	ε(f) = f(1G)	S(f)(x) = f(x−1)	네	만약 G가 아벨리안이라면
컴팩트 그룹의 대표 기능	콤팩트 그룹 G	Δ(f)(x,y) = f(xy)	ε(f) = f(1G)	S(f)(x) = f(x−1)	네	만약 G가 아벨리안이라면	반대로, 유한한 하아 적분으로 C에 대한 모든 교감적 비자발적 감소 Hopf 대수학은 이러한 방식으로 발생하며, Tannaka-Krein 이중성의 하나의 공식화를 제공한다.[15]
대수군에서의 정규 함수		Δ(f)(x,y) = f(xy)	ε(f) = f(1G)	S(f)(x) = f(x−1)	네	만약 G가 아벨리안이라면	반대로, 한 분야에 걸친 모든 역행 홉프 대수학은 이런 방식으로 집단적 계획으로부터 발생하며, 범주의 반정밀성을 부여한다.[16]
텐서 대수 T(V)	벡터 스페이스 V	Δ(x) = x ⊗ 1 + 1 ⊗ x, x in V, Δ(1) = 1 ⊗ 1	ε(x) = 0	S(x) = 'T(V1)의 모든 x에 대해 -x(그리고 더 높은 텐서 파워로 확장)	dim(V)=0,1인 경우에만	네	대칭 대수 및 외부 대수(텐서 대수의 인용구)도 콤멀티제이션, 카운티 및 대척점에 대한 이 정의를 가진 홉프 알제브라함이다.
범용포락 대수 U(g)	리 대수 g	Δ(x) = g의 모든 x에 대해 x x 1 + 1 ⊗ x (이 규칙은 정류자와 호환되므로 U 전체로 고유하게 확장될 수 있음)	ε(x) = 모든 x in g에 대해 0(again, U로 확장)	S(x) = −x	만약 g가 아벨리안이라면	네
스위들러의 Hopedler 대수 H=K[c2, x]/c2 = 1, x = 0, xc = -c = -cx.	K는 2와 다른 특성을 가진 분야다.	Δ(c) = c ⊗ c, Δ(x) = c ⊗ x + x ⊗ 1, Δ(1) = 1 ⊗ 1	ε(c) = 1 및 ε(x) = 0	S(c) = c−1 = c 및 S(x) = -cx	아니요.	아니요.	기본 벡터 공간은 {1, c, x, cx}에 의해 생성되므로 차원 4가 있다. 이것은 홉프 대수학의 가장 작은 예로서, 둘 다 비법용과 비법용이다.
대칭 함수의 고리[17]		완전한 동종 대칭 함수k h (k ≥ 1): Δ(hk) = 1⊗ hk + h h1k−1 h + ... + hk−1 ⊗ h + h1k ⊗ 1.	ε(hk) = 0	S(hk) = (−1)k ek	네	네

유한 그룹의 기능은 그룹 링과 함께 식별될 수 있다는 점에 유의하십시오. 그룹 링은 보다 자연스럽게 이중으로 생각되지만, 그룹 링은 유한한 양의 원소로 구성되며, 따라서 총합된 원소의 함수를 평가하여 그룹 상의 기능과 쌍을 이룬다.

리 그룹의 코호몰로지

Lie $그룹{\displaystyle }$ G ${\displaystyle G}$의 코호몰로지 대수($필드{\displaystyle }$ K ${\displaystyle K}$)는$$ Hopf 대수학이며, 곱셈은 컵 제품에 의해 제공되며, 곱셈은 배합된다.

${\displaystyle H^{*}(G,K)\오른쪽 화살표 H^{*}(G\time G,K)\cong H^{*(G,K)\otimes H^{*}(G,K)}}$

그룹 곱셈 $G{\displaystyle }$ ${\displaystyle \times }$ ${\displaystyle G}$→ ${\displaystyle G}$ ${\displaystyle G\time G\to G}$에 의해$.$ 이 관찰은 사실 홉프 대수학의 개념의 원천이었다. 이 구조를 이용하여 홉프는 리 그룹의 코호몰로지 대수학을 위한 구조 정리를 증명했다.

정리(Hopf)^[18] $Let{\displaystyle }$ A ${\displaystyle A}$특성 0의 분야에 걸쳐 유한 차원, 등급이 매겨진 정류형, 등급이 매겨진 코코뮤트식 Hopf 대수학이다$$. 그러면 $A{\displaystyle }$ ${\displaystyle A}($대수로서)는 홀수 정도의 발전기를 가진 자유 외부 대수다.

양자 그룹 및 비확정 기하학

위의 모든 예는 역법(즉, 곱셈은 역법) 또는 동일법률(즉,^[19] 트위스트^[20] 맵 T: H → H → H ⊗ H가 T(x y y) = y x x로 정의되는 경우 Δ = T Δ). 다른 흥미로운 홉프 알헤브라는 상호 작용적이거나 공동 커밋되지 않는 사례 3의 변형 또는 "정량화"가 확실하다. 이 홉프 알헤브라는 종종 양자 그룹이라고 불리는데, 이 용어는 지금까지 느슨하게 정의되어 있을 뿐이다. 그것들은 비고정 기하학에서 중요한데, 아이디어는 다음과 같다: 표준 대수 집단은 정규 함수의 표준 호프 대수학으로 잘 묘사된다; 그러면 우리는 이 호프 대수학의 기형적인 버전을 특정한 "비표준" 또는 "정량화된" 대수집단을 기술하는 것으로 생각할 수 있다(이것은 전혀 대수집단이 아니다). 이러한 비표준 물체를 정의하거나 조작하는 직접적인 방법은 없어 보이지만, 여전히 홉프 알헤브라와 함께 작업할 수 있으며, 실제로 홉프 알헤브라와 동일시한다. 그래서 "퀀텀 그룹"이라는 이름이 붙었다.

표현 이론

A를 호프 대수학으로 하고, M과 N을 A-모듈로 한다. 그렇다면 M ⊗ N도 A-module로 되어 있는데, 이 A-module은 다음과 같다.

$(m\displaystyle a(m\times n):=\Delta (a)(m\otimes n)=(a_{1}\otimes a_{2}(m\otimes n)=(a_{1}m\otimes a_{2}n)}}$

m ∈ M, n ∈ N 및 Δ(a) = (a₁, a₂)의 경우. 나아가 사소한 표현을 K의 베이스 필드 K로 정의할 수 있다.

$[\displaystyle a(m):=\엡실론(a)m}$

M ∈ K의 경우. 마지막으로, A의 이중 표현을 정의할 수 있다: M이 A-모듈이고 M*이 이중 공간이라면,

${\displaystyle (af)(m):=f(S(a)m)}$

여기서 f ∈ M* 및 m ∈ M.

Δ, ε, S의 관계는 벡터 공간의 특정한 자연 동형성이 실제로 A-모듈의 동형성이라는 것을 보장한다. 예를 들어 벡터 공간 M → M ⊗ K 및 M → K ⊗ M의 자연 이형성 역시 A-모듈의 이형성이다. 또한 f ⊗ m → f(m)이 있는 벡터 공간 M* ⊗ M → K의 지도도 A-module의 동형상이다. 단, 지도 M ⊗ M* → K는 반드시 A-모듈의 동형상일 필요는 없다.

관련개념

Graded Hopf Algebras는 대수적 위상에 종종 사용된다: 그것들은 H-space의 모든 호몰로지 또는 코호몰로지 그룹의 직접적인 합에 있는 자연적인 대수적 구조다.

국지적으로 콤팩트한 양자 그룹은 홉프 알헤브라를 일반화하고 토폴로지를 운반한다. Lie 그룹의 모든 연속함수의 대수는 국소적으로 압축된 양자군이다.

준홉프 알제브라는 홉프 알제브라를 일반화한 것으로, 협동조합성은 반전을 지탱할 뿐이다. 그것들은 크니즈니크-자몰로드치코프 방정식의 연구에 사용되어 왔다.^[21]

1994년^[22] 알폰스 반 대엘이 도입한 곱셈 홉프 알제브라는 대수(단위 유무 유무)에서 그 자체로 대수의 텐서 제품 대수의 곱셈 대수에 이르는 홉프 알제브라의 일반화다.

2000년 V. G. 투라예프가 선보인 홉프 그룹-(co)알제브라도 홉프 알제브라의 일반화다.

약한 홉프 알헤브라스

약한 호프알게브라스, 또는 양자 그룹오이드들은 호프알게브라의 일반화다. 홉프 알헤브라와 마찬가지로 약한 홉프 알헤브라는 자기 이중 계급을 형성한다. 즉, 만약 H가 (약) 홉프 대수라면 H*에 대한 선형 형태의 이중 공간(H*와 그것의 결합과 그 결합-알제브라 구조에서 얻은 대수-연석 구조와 관련)이다. 약한 홉프 대수 H는 보통 a로 간주된다.

• 합금 Δ: H → H → H 및 상담 ε: H → 홉프 대수의 모든 공리를 만족하는 유한 치수 대수 및 합금 δ: H → k 홉프 대수의 모든 공리를 만족하는 Δ(1) ≠ 1 ⊗ 1 또는 ε(ab) ≠(b) ≠(b)의 일부 a,b. 대신 다음과 같은 사항을 요구한다.

${\deltayle(\Delta(1)\otimes 1)(1\otimes \Delta(1)=(\Delta(1)\Delta(1))=(\Delta \otimes{\mbox{Id})}\Delta(1)}$

$\displaystyle \epsilon (iii)=\sum \epsilon (ab_{(1)}\epsilon (b_{(2)c)=\sum \epsilon (ab_{(2)}\epsilon (b_{(1)}c)}}$

모든 a, b, c in H에 대해.

• H는 공리를 만족시키는 약화된 항정신병 S: H → H를 가지고 있다.

1. ${\displaystyle S(a_{(1)})a_{(2)}=1_{(1)}\epsilon (a1_{(2)})}$ for all a in H (the right-hand side is the interesting projection usually denoted by Π^R(a) or ε_s(a) with image a separable subalgebra denoted by H^R or H_s);
2. ${\displaystyle a_{(1)}S(a_{(2)})=\epsilon (1_{(1)}a)1_{(2)}}$ for all a in H (another interesting projection usually denoted by Π^R(a) or ε_t(a) with image a separable algebra H^L or H_t, anti-isomorphic to H^L via S);
3. ${\displaystyle S}$(${\displaystyle {}_{}}$( ${\displaystyle 1_{}}$) ${\displaystyle {}_{}}$ (${\displaystyle {}_{}{}_{}}$) ${\displaystyle {\mathrm{a}}_{}}$ (${\displaystyle {}_{}}$3${\displaystyle {}_{}))}$ =${\displaystyle S}$ (${\displaystyle }$) ${\displaystyle S(a_{(1)}a_{(2)S(a_{(3)}}=S(a)}}$는 모든 A의 경우$$.

Δ(1) = 1 μ1일 경우, 이러한 조건은 Hopf 대수 대수의 대척점에 있는 두 가지 일반적인 조건으로 줄어든다는 점에 유의한다.

공리는 부분적으로 선택되어 H-모듈의 범주가 경직된 단면체 범주가 된다. 단위 H-모듈은 위에서 언급한 분리 가능한 대수 H이다^L.

예를 들어 유한집단대수는 약한 홉프 대수다. 특히 [n]에서 i와 j 사이에 하나의 반전성 화살표 e와_ij e 쌍이_ji 있는 [n]의 조로이드 대수학(groupoid 대수학)은 n x n 행렬의 대수 H와 이형성이다. 이 특정 H에 대한 약한 Hopf 대수 구조는 coproduct_ij Δ_ij(e) = e ⊗ e_ij, 카운티_ij =(e) = 1 및 대척점 S(e_ij) = e에_ji 의해 주어진다. 분리 가능한 아발게브라^L H와 H는^R 일치하며 이 특별한 경우(대각 행렬의 아발게브라)에서 중심적이지 않은 교감 알제브라이다.

약한 홉프 알제브라에 대한 초기 이론적 기여는 또한^[24] 에서^[23] 발견될 것이다.

호프알제브로이드

Hopf 알헤브로이드 참조

그룹과의 유사성

그룹은 Hopf 대수로서 동일한 도표(동일하게, 연산)에 의해 공리화될 수 있으며, 여기서 G는 모듈 대신 집합으로 간주된다. 이 경우:

• 필드 K는 1점 세트로 대체된다.
• 자연 상담이 있다(1점 만점에 지도)
• 자연복제법(대각선 지도)이 있다.
• 단위는 그룹의 ID 요소다.
• 곱셈은 그룹의 곱셈이다.
• 대척점은 역이다.

이 철학에서 집단은 "하나의 요소가 있는 분야"^[25]를 넘어 홉프 대수학이라고 생각할 수 있다.

땋은 단면체 범주의 홉프 알헤브라스

홉프 대수학의 정의는 자연스럽게 임의의 땋은 단면체 범주로 확장된다.^[26][27] A Hopf algebra in such a category ${\displaystyle (C,\otimes ,I,\alpha ,\lambda ,\rho ,\gamma )}$ is a sextuple ${\displaystyle (H,\nabla ,\eta ,\Delta ,\varepsilon ,S)}$ where ${\displaystyle H}$ is an object in ${\displaystyle C}$, and

${\displaystyle \nabla$$$$H\time H\to$ H$}($증배),

${\displaystyle \eta$$$$I\to H}$ ($$단위)

${\디스플레이$$$$H\to H\otimes$ H$}($복제)

${\displaystyle \varepsilon$$$$H\to I}$ ($$상담)

${\디스플레이 스타일$$H\to$ H$}($antipode)

— 다음과 같은$$ $C{\displaystyle }$ ${\displaystyle C}$의 형태.

1) the triple ${\displaystyle (H,\nabla ,\eta )}$ is a monoid in the monoidal category ${\displaystyle (C,\otimes ,I,\alpha ,\lambda ,\rho ,\gamma )}$, i.e. the following diagrams are commutative:^[28]

2) the triple ${\displaystyle (H,\Delta ,\varepsilon )}$ is a comonoid in the monoidal category ${\displaystyle (C,\otimes ,I,\alpha ,\lambda ,\rho ,\gamma )}$, i.e. the following diagrams are commutative:^[28]

3) $H{\displaystyle }$ ${\displaystyle H}$에 있는 모노이드와 코모노이드의 구조는 호환된다$$: 곱셈$\$ {\$displaystyle$ \$nabla$}과$$ 단위 $\eta {\displaystyle }$ ${\displaystyle \eta$}은$$ 코모노이드의 형태이며, (이러한 상황은 동일하다) 복합 $\Delta {\displaystyle \mathrm{}}$ ${\delta}$과 상담 $\.$${\displaystyle \varepsilon }$은(는) 모노이드의 형태로서, 다음과 같은 도표가 일치해야 함을 의미한다.^[29]

the quintuple ${\displaystyle (H,\nabla ,\eta ,\Delta ,\varepsilon )}$ with the properties 1),2),3) is called a bialgebra in the category ${\displaystyle (C,\otimes ,I,\alpha ,\lambda ,\rho ,\gamma )}$;

4) 대척점 도표는 다음과 같다.

대표적인 예는 다음과 같다.

• 그룹. 단일 범주$({\displaystyle \text{Set}}$ ,${\displaystyle \times }$, 1${\displaystyle }$)에서 ${\displaystyle({\text})$$Set}},\times ,1)}$ of sets (with the cartesian product ${\displaystyle \times }$ as the tensor product, and an arbitrary singletone, say, ${\displaystyle 1=\{\varnothing \}}$, as the unit object) a triple ${\displaystyle (H,\nabla ,\eta )}$ is a monoid in the categorical sense if and only if it is a monoid in the usual algebraic sense, i.e. if the operations ${\displaystyle \nabla (x,y)=x\cdot y}$ and ${\displaystyle \eta (1)}$ behave like usual multiplication and unit in ${\displaystyle H}$ (but possibly without the invertibility of elements ${\displaystyle x\in H}$). At the same time, a triple ${\displaystyle (H,\Delta ,\varepsilon )}$ is a comonoid in the categorical sense iff ${\displaystyle \Delta }$ is the diagonal operation ${\displaystyle \Delta (x)=(x,x)}$ (and the operation ${\displaystyle \varepsilon }$ is defined uniquely as well: ${\displaystyle \epsilon (}$${\displaystyle x}$)${\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle \varepsilon (x)=1$} $$. 그리고 그러한 코모노이드$({\displaystyle H}$, ${\displaystyle \mathrm{\Delta }}$ ,$$${\displaystyle \epsilon }$)의 어떤$$구조도(H,\$Delta ,\$$varemsilon$$$)는$$ 정의의 3절의 도표가 항상 통근한다는 점에서$$ $모노이드(H$ , ∇ ,$η$)의 어떤 구조와도 호환된다. 각 모노이드$({\displaystyle H,}$ ${\displaystyle \mathrm{\nabla ,}\eta }$ ) ${\displaystyle(H,\nabla ,\$${\displaystyle \mathrm{eta}}$ $)}$의${\displaystyle }$(${\displaystyle \text{Set}}$ ,${\displaystyle \times }$, 1${\displaystyle }$) ${\displaystyle({\text})$$세트},\times,1)}$은$({\displaystyle }$는) 자연스럽게 (${\displaystyle \text{세트}}$,${\displaystyle \times }$ , ${\displaystyle 1}$)에서$$ 바이알게브라$({\displaystyle H}$ ,${\displaystyle \mathrm{\nabla }}$ , ${\displaystyle ,}$ , ${\displaystyle \Delta }$ ,${\displaystyle )}$ ) ${\displaystyle (H,\nabla$,\$eta$,\$Delta ,\varepsilon )}$로 간주할 수 있다$$$({\$$text$}).$설정},\time,1)} 또는$ 그 반대의 경우도 마찬가지 입니다$.$ 대척점 $S{\displaystyle }$: ${\displaystyle H}$→ ${\displaystyle H}$ ${\디스플레이$ 스타일 S$:$$H\to H}$ for such a bialgebra ${\displaystyle (H,\nabla ,\eta ,\Delta ,\varepsilon )}$ means exactly that every element ${\displaystyle x\in H}$ has an inverse element ${\displaystyle x^{-1}\in H}$ with respect to the multiplication ${\displaystyle \nabla (x,y)=x\$$cdot y}$. 따라서 집합 범주$({\displaystyle \text{Set}}$ ,${\displaystyle \times }$, 1${\displaystyle }$)에서 ${\displaystyle({\text{)$$세트},\times,1)$홉프$$ 알제브라는 통상적인 대수적 의미에서 정확하게 집단이다.
• 고전적인 홉프 알헤브라스. In the special case when ${\displaystyle (C,\otimes ,s,I)}$ is the category of vector spaces over a given field ${\displaystyle K}$, the Hopf algebras in ${\displaystyle (C,\otimes ,s,I)}$ are exactly the classical Hopf algebras described above.
• 그룹 내 기능 알제브라함 The standard functional algebras ${\displaystyle {\mathcal {C}}(G)}$, ${\displaystyle {\mathcal {E}}(G)}$, ${\displaystyle {\mathcal {O}}(G)}$, ${\displaystyle {\mathcal {P}}(G)}$ (of continuous, smooth, holomorphic, regular functions) on groups are Hopf algebras in the catego고정관념 공간의 라이${\displaystyle }$Ste,$display$ {\$displaystyle$odot }^[30] )
• 알제브라 그룹. The stereotype group algebras ${\displaystyle {\mathcal {C}}^{\star }(G)}$, ${\displaystyle {\mathcal {E}}^{\star }(G)}$, ${\displaystyle {\mathcal {O}}^{\star }(G)}$, ${\displaystyle {\mathcal {P}}^{\star }(G)}$ (of measures, distributions, analytic fu그룹의 nectionals와 currents)는 고정관념 공간의 범주(Ste, ⊛, ${\displaystyle }$ ${\displaystyle \circledast }$)에 있는 Hopf 알제브라다.^[30] 이 홉프 알제브라는 비확정 집단을 위한 이중성 이론에 사용된다.^[31]

참고 항목

• 콰시트리올 호프 대수
• 대수/유추 설정
• 홉프알제브라의 표현 이론
• 리본 호프 대수
• 수페랄게브라
• 슈퍼그룹
• 애니오닉 리 대수
• 스위들러의 호프 대수
• 순열의 호프 대수
• 밀너-모어 정리

참고 및 참조

메모들

참조

• Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001), Hopf Algebras. An introduction, Pure and Applied Mathematics, vol. 235 (1st ed.), Marcel Dekker, ISBN 978-0-8247-0481-0, Zbl 0962.16026.
• Cartier, Pierre (2007), "A Primer of Hopf Algebras", in Cartier, P.; Moussa, P.; Julia, B.; Vanhove, P. (eds.), Frontiers in Number Theory, Physics, and Geometry, vol. II, Berlin: Springer, pp. 537–615, doi:10.1007/978-3-540-30308-4_12, ISBN 978-3-540-30307-7
• Fuchs, Jürgen (1992), Affine Lie algebras and quantum groups. An introduction with applications in conformal field theory, Cambridge Monographs on Mathematical Physics, Cambridge: Cambridge University Press, ISBN 978-0-521-48412-1, Zbl 0925.17031
• 하인츠 홉프, 우버 다이 투톨로지 데어 그루펜-만니그팔트키텐 und ihrer Veralgemeinerungen, 수학의 연보 42 (1941), 22–52. 베를린 스프링거 119-151페이지 셀렉타 하인츠 홉프에서 재인쇄되었다. MR4784, Zbl 0025.09303
• Montgomery, Susan (1993), Hopf algebras and their actions on rings, Regional Conference Series in Mathematics, vol. 82, Providence, Rhode Island: American Mathematical Society, ISBN 978-0-8218-0738-5, Zbl 0793.16029
• Street, Ross (2007), Quantum groups: A Path To Current Algebra, Australian Mathematical Society Lecture Series, vol. 19, Cambridge University Press, ISBN 978-0-521-69524-4, MR 2294803, Zbl 1117.16031.
• Sweedler, Moss E. (1969), Hopf algebras, Mathematics Lecture Note Series, W. A. Benjamin, Inc., New York, ISBN 9780805392548, MR 0252485, Zbl 0194.32901
• Underwood, Robert G. (2011), An introduction to Hopf algebras, Berlin: Springer-Verlag, ISBN 978-0-387-72765-3, Zbl 1234.16022
• Turaev, Vladimir; Virelizier, Alexis (2017), Monoidal Categories and Topological Field Theory, Progress in Mathematics, vol. 322, Springer, doi:10.1007/978-3-319-49834-8, ISBN 978-3-319-49833-1.
• Akbarov, S.S. (2003). "Pontryagin duality in the theory of topological vector spaces and in topological algebra". Journal of Mathematical Sciences. 113 (2): 179–349. doi:10.1023/A:1020929201133. S2CID 115297067.
• Akbarov, S.S. (2009). "Holomorphic functions of exponential type and duality for Stein groups with algebraic connected component of identity". Journal of Mathematical Sciences. 162 (4): 459–586. arXiv:0806.3205. doi:10.1007/s10958-009-9646-1. S2CID 115153766.