등가 임피던스 변환

선형 네트워크 분석
요소들
구성 요소들
직렬 및 병렬 회로
임피던스 변환
발전기 정리	네트워크 정리
네트워크 분석 방법
2포트 파라미터
	보다 말해라.

등가 임피던스는 임피던스^{[note 2]} 소자의 전기 네트워크의 등가 회로로, 모든 단자 쌍 간에 주어진^{[note 10]} 네트워크와 동일한 임피던스를 제공합니다.이 문서에서는 전자 회로에서 일반적으로 볼 수 있는 일부 수동 선형 임피던스 네트워크 간의 수학적 변환에 대해 설명합니다.

선형 네트워크 분석에는 매우 잘 알려져 있고 자주 사용되는 등가 회로가 많이 있습니다.여기에는 직렬 저항, 병렬 저항 및 캐패시터, 인덕터 및 일반 임피던스용 직렬 및 병렬 회로로의 확장이 포함됩니다.Y-Ω 변환과 마찬가지로 Norton 및 Thévenin 등가 전류 발생 회로와 전압 발생 회로도 잘 알려져 있습니다.여기에서는 이들 중 어느 것도 상세하게 설명하지 않습니다.개개의 링크 기사를 참조해 주세요.

선형 네트워크를 변환할 수 있는 등가 회선의 수는 무제한입니다.가장 사소한 경우에도 예를 들어 병렬로 몇 개의 다른 저항 조합이 주어진 결합 저항과 동일한지 물어보면 이것이 사실임을 알 수 있습니다.형성할 수 있는 직렬 및 병렬 조합의 수는 저항의 수 n에 따라 기하급수적으로 증가합니다.큰 n의 경우 집합의 크기가 약 2.53인ⁿ 것으로 수치 기법에 의해 확인되었으며 분석적으로 엄격한 경계가 피보나치 숫자의 ^[1]Farey 시퀀스에 의해 주어진다.이 기사는 결코 포괄적이기를 바랄 수 없지만, 몇 가지 일반화가 가능하다.빌헬름 코어는 ^{[note 9]}주어진 유리, 수동, 선형 1포트, 즉 주어진 ^{[note 8]}2단자 임피던스의 모든 가능한 등가물을 생성할 수 있는 변환을 발견했습니다.4단말기, 특히 2포트 네트워크의 변환도 일반적이며 보다 복잡한 네트워크의 변환도 가능합니다.

등가 회로에 관한 토픽의 방대한 규모는 시드니 달링턴의 이야기에서 강조된다.Darlington에 따르면, Ronald M에 의해 상당수의 동등한 회로가 발견되었다. 포스터는 1920년 조지 캠벨과 함께 논파괴 4포트에 관한 논문을 발표하였습니다.이 작업에서는 4개의 포트를 이상적인 변압기와^{[note 5]} 최대 전력 전송으로 상호 연결할 수 있는 방법을 검토했습니다.그들은 실용적으로 적용될 수 있는 여러 가지 조합을 찾아 AT&T 특허 부서에 특허를 요청했습니다.특허청은 경쟁사가 동등한 회로를 사용해 특허를 회피할 수 있다면 일부 회로를 특허화하는 것은 무의미하다고 답했다.그래서 포스터는 그들 모두를 계산하기 시작했다.그는 총 83,539개의 동등물(다른 생산 비율을 포함할 경우 577,722개)에 도달했다.이는 특허가 되기에는 너무 많았기 때문에 AT&T의 경쟁사가 향후 특허를 ^[2][3]취득하는 것을 막기 위해 그 정보가 공개되었다.

2단말기, 2단말기 종류의 네트워크

단일 임피던스에는 외부 세계에 접속하기 위한 2개의 단자가 있기 때문에 2단자 또는 1포트 네트워크라고 할 수 있습니다.그 간단한 설명에도 불구하고, meshes,[노트 6]의 수 그리고 복잡성과 요소의 개수에는 한계가 없은 임피던스 네트워크 가질 수 있다. 2-element-kind[노트 4]네트워크 회로 설계에서 흔히 볼 수 있다. 예를 들면 필터, 종종LC-kind 네트워크와 인쇄 회로 디자이너들을 지지하는 RC-kind 네트워크 때문 inductors 있다. 덜 쉽다제조하는 것입니다.변환은 3-element 유형의 네트워크보다 간단하고 쉽게 찾을 수 있습니다.1 엘리먼트 타입의 네트워크는 2 엘리먼트 타입의 특수한 경우라고 생각할 수 있습니다.요소_n Z의 네트워크를 요소 Z의 네트워크로 대체함으로써 특정 3 요소 종류의 네트워크에서 이 섹션의 변환을 사용할 수 있습니다.단, 이것은 대체되는 최대 2개의 임피던스로 제한됩니다.나머지는 자유로운 선택이 아닙니다.이 절에서 설명하는 변환 방정식은 모두 오토 ^[4]조벨에 의한 것입니다.

3 슬롯 네트워크

1 요소 네트워크는 사소하고 ^{[note 3]}2 요소 2 터미널 네트워크는 직렬 또는 병렬의 2 요소 중 하나이며, 이것도 사소합니다.사소하지 않은 요소의 최소 수는 3개이며,^[5] 2가지 요소 종류의 사소하지 않은 변환이 가능합니다.하나는 역변환과 토폴로지 이중입니다.

묘사	네트워크	변환 방정식	변환된 네트워크
트랜스폼 1.1 트랜스폼 1.2는 이 트랜스폼의 반대입니다.		${\displaystyle p_{1}=1+m_{1}\,}$ ${\displaystyle p_{2}=m_{1}(1+m_{1})\,}$ ${\displaystyle p_{3}=(1+m_{1})^{2}\ .}$
트랜스폼 1.2 Transform 1.1의 역변환 및 토폴로지 이중.		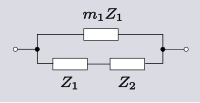${{displaystyle p_{1}=black {{m_{1}}^2}}{1+m_{1}}}}\ ,}$ ${\displaystyle p_{2}=black {m_{1}}{1+m_{1}}}}\ ,}$ ${\displaystyle p_{3}=\leftflac {m_{1}}{1+m_{1}}}\오른쪽)^{2}\ .}$
예 1. Transform 1.2의 예.인덕터의 크기를 줄이면 실질적인 이점이 있습니다.		${\displaystyle m_{1}=0.5\,}$ ${\displaystyle p_{1}=\textstyle {frac {1}{6}}\,}$ ${\displaystyle p_{2}=\textstyle {frac {1}{3}}\,}$ ${\displaystyle p_{3}=\textstyle {frac {1}{9}}\ .}$

4 슬롯 네트워크

2-element-kind 네트워크에는 4가지 중요하지 않은 4가지 요소 변환이 있습니다.이 중 2개는 다른 2개의 역변환이고 2개는 다른 2개의 역변환입니다.Z가 Z와 같은₁ 요소 종류로 되어 있는₂ 특수한 경우, 즉 네트워크가 1 요소 종류로 축소되어 있는 경우, 한층 더 변환이 가능하다.요소의 수가 증가함에 따라 가능한 네트워크의 수는 계속 증가하고 있습니다.다음 표의 모든 엔트리에 대해 ^[6]정의됩니다.

${\displaystyle {q\mathrm{}}_{}}$1 : ${\displaystyle ={}_{}}$+ ${\displaystyle {m1\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {m2\mathrm{}}_{}{}_{}}$({ $displaystyle q_{1}$ : $= 1$ + $m$_ {2} , \ !$$} , ${\displaystyle {q\mathrm{}}_{}}$2 : $=$ 1${\displaystyle \sqrt{{}^{}{{}_{}}^{\mathrm{}}}}$ - ${\displaystyle \sqrt{4}}$ ${\displaystyle \sqrt{{}_{}}}$ ${\displaystyle \sqrt{{}_{}{}_{}}}$ ${\displaystyle \sqrt{{m2\mathrm{}}_{}}\sqrt{{}_{}}}$({ $displaystyle q$_ { 2} := $scaprt${{q$$_$${1} } - 4$m$_ {2} m$_$ {2} ,$$\ !}$$ , ${\displaystyle {q\mathrm{}}_{}}$ 3${\displaystyle {}_{}}$: ${\displaystyle =\frac{}{}}$ (${\displaystyle \frac{}{}}$1 + ${\displaystyle \frac{{}_{}{1\mathrm{}}_{}}{}}$) ( ${\displaystyle \frac{1}{}}$+ ${\displaystyle \frac{{m\mathrm{}}_{}}{}}$2${\displaystyle \frac{}{}}$) ( ${\displaystyle \frac{{m\mathrm{}}_{}{}_{}}{}}$ - ${\displaystyle \frac{{m\mathrm{}}_{}{}^{}}{}}$2 )$$ ( { $displaystyle q$_ { 3 } : =$superfrac${ ($1$+ $m$_ {$1$} ) { ( $1$+ $m$_ { $2$} } } { ( m$$_ { 2$$} ) $$} 、

${\displaystyle {q\mathrm{}}_{}}$ 4${\displaystyle {}_{}}$: ${\displaystyle =\frac{{q\mathrm{}}_{}}{}}$2 - ${\displaystyle \frac{{q\mathrm{}}_{}}{}}$1 + ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ ${\displaystyle \frac{{q\mathrm{}}_{}}{}}$ 2$$q 2 q 2 q 2 q 2 q 2 : =$specfrac {q_{2$} - $q_{1}+2m_{2}}},$ ${\displaystyle {q\mathrm{}}_{}}$ 5${\displaystyle {}_{}}$: ${\displaystyle =\frac{{}_{}{}_{}}{}}$2 + ${\displaystyle \frac{{q\mathrm{}}_{}1}{}}$ - ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{{}_{}}{\mathrm{}}}$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{{q\mathrm{}}_{}}{}}$ 2$$q 2 q 2 ({ displaystyle $q$_ { 5 : =$specfrac${ $q$_ {$}$ + $q$_ {1} - 2$m _$ ${$2$}$} } $$。

묘사	네트워크	변환 방정식	변환된 네트워크
트랜스폼 2.1 트랜스폼 2.2는 이 트랜스폼의 반대입니다.트랜스폼 2.3은 이 트랜스폼의 토폴로지 듀얼입니다.		${\displaystyle p_{1}=syslogfrac {q_{1}+q_{2}}{2q_{5}}\,}$ ${\displaystyle p_{2}=syslogfrac {q_{1}-q_{2}}{2q_{4}}\,}$ ${\displaystyle p_{3}=syslogfrac {m_{2}}{q_{5}}\,}$ ${\displaystyle p_{4}=syslogfrac {m_{2}}{q_{4}}\ .}$
트랜스폼 2.2 트랜스폼 2.1은 이 트랜스폼의 반대입니다.트랜스폼 2.4는 이 트랜스폼의 토폴로지 이중입니다.		${\displaystyle p_{1}=paramfrac {1}{q_{3}(1+m_{2})}}\,}$ ${\displaystyle p_{2}=black {m_{1}}{1+m_{1}}}}\ ,}$ ${\displaystyle p_{3}=paramfrac {1}{q_{3}(1+m_{1}}}}\,}$ ${\displaystyle p_{4}=black {m_{2}}{1+m_{2}}}}\ .}$
트랜스폼 2.3 트랜스폼 2.4는 이 트랜스폼의 반대입니다.트랜스폼 2.1은 이 트랜스폼의 토폴로지 듀얼입니다.		${\displaystyle p_{1}=black {q_{4}(q_{1}+q_{2})}{2m_{2}}\,}$ ${\displaystyle p_{2}=black {q_{5}(q_{1}-q_{2}){2m_{2}}\,}$ ${\displaystyle p_{3}=q_{4}\,}$ ${\displaystyle p_{4}=q_{5}\ .}$
Transform 2.4 트랜스폼 2.3은 이 트랜스폼의 반대입니다.트랜스폼 2.2는 이 트랜스폼의 토폴로지 듀얼입니다.		${\displaystyle p_{1}=1+m_{1}\,}$ ${\displaystyle p_{2}=m_{1}q_{3}(1+m_{1}\,}$ ${\displaystyle p_{3}=1+m_{2}\,}$ ${\displaystyle p_{4}=m_{1}q_{3}(1+m_{2})\ .}$
예 2 Transform 2.2의 예.		${\displaystyle m_{1}=3\,}$ ${\displaystyle m_{2}=1\,}$ ${\displaystyle q_{3}=2\,}$ ${\displaystyle p_{1}=\textstyle {frac {1}{4}}\,}$ ${\displaystyle p_{2}=\textstyle {frac {3}{4}}\,}$ ${\displaystyle p_{3}=\textstyle {frac {1}{8}}\,}$ ${\displaystyle p_{4}=\textstyle {frac {1}{2}}\ .}$

2단말기, n단말기, 3단말기 종류의 네트워크

Kirchhoff의 법칙과 같은 단순한 네트워크 이론의 적용으로 네트워크 방정식을 "수동으로" 공식화함으로써 몇 가지 요소로 구성된 단순한 네트워크를 처리할 수 있습니다.두 개의 방정식을 직접 비교하고 계수를 등가함으로써 두 네트워크 간의 동등성을 증명합니다.대규모 네트워크에서는 보다 강력한 기술이 필요합니다.일반적인 접근방식은 우선 임피던스 네트워크를 매트릭스로 표현하는 것입니다.이 접근방식은 합리적인 네트워크에서만^{[note 9]} 유효합니다.전송선 등의 분산 요소를 포함하는 네트워크는 유한 매트릭스로 나타낼 수 없습니다.일반적으로 n-mesh^{[note 6]} 네트워크에서는 nxn 매트릭스가 필요합니다.예를 들어 3-메쉬 네트워크의 매트릭스는 다음과 같습니다.

${\displaystyle \mathbf {[Z]} = begin {bmatrix}Z_{11}&Z_{13}&Z_{212}&Z_{22}&Z_{23}&Z_{31}&Z_32}&Z_33}\endmatrix}$

매트릭스의 엔트리는 매트릭스가 메시 전압 및 전류에서 선형 방정식의 시스템을 형성하도록 선택됩니다(메쉬 분석을 위해 정의된 대로).

$\displaystyle \mathbf {[V]} = \mathbf {[Z][I]} } }$

예를 들어 그림 1의 예도는 다음과 같이 임피던스 행렬로 나타낼 수 있습니다.

${\displaystyle \mathbf {[Z]}=begin {bmatrix}R_{1}+R_{2}\\-R_{2}+R_{3}\end{bmatrix}}$

그리고 선형 방정식의 관련 체계는

${\displaystyle {bmatrix}V_{1}\0\end{bmatrix}={begin{bmatrix}R_{1}+R_{2}&R_{2}+R_{2}+R_{3}\end{matrix}\{begin}\{batrix}={begin}I_{1}\\I_{2}\end{bmatrix}}$

가장 일반적인 경우 네트워크의^{[note 1]} 각 브랜치Z는_p 3개의 요소로 구성되므로

${\displaystyle Z_{\mathrm {p} = sL_{\mathrm {p} } + {1 \over sC_{\mathrm {p} }}$

여기서 L, R 및 C는 각각 인덕턴스, 저항 및 캐패시턴스를 나타내며, s는 $복소{\displaystyle }$ 주파수 연산자 ${\displaystyle s=}$ ${\displaystyle i}$ + ${\displaystyle i}$ ${\$ { $displaystyle$ \$scriptstyle$ s$=$ \$displaystyle + i\obe$ $\}$입니다.

이것은 일반적인 임피던스를 나타내는 일반적인 방법이지만, 이 문서의 목적상 캐패시턴스의 역수인 탄성 D, C를 처리하는 것이 수학적으로 더 편리합니다.이러한 관점에서 일반적인 분기 임피던스는 다음과 같이 나타낼 수 있습니다.

${\displaystyle sZ_{\mathrm {p}}=s^{2}L_{\mathrm {p}+sR_{\mathrm {p}}+D_{\mathrm {p}},\!}$

마찬가지로 임피던스 매트릭스의 각 엔트리는 3개의 요소의 합으로 구성될 수 있습니다.따라서 행렬은 3가지 요소 종류 각각에 대해 1개씩 3개의 nxn 행렬로 분해할 수 있습니다.

${\displaystyle s\mathbf {[Z]} =s^{2}\mathbf {[L]} +\mathbf {D]}$

행렬 [Z]는 임피던스 Z를 나타내는 것이 바람직합니다.이를 위해 메시 중 하나의 루프가 절단되고 Z(s)는 절단된 지점 사이에서 측정된 임피던스입니다.외부접속포트는 메쉬1에 있기 때문에 매트릭스엔트리₁₁ Z에 걸쳐 접속되어 있다고 가정하는 것이 일반적이지만 원하는 ^{[note 7]}노드에 대한 접속을 사용하여 이를 공식화할 수 있습니다.다음 논의에서 Z를 가로질러₁₁ 취해진 Z(s)를 가정한다. Z(s)는 다음과 같이 [Z]에서^[7] 계산할 수 있다.

${\displaystyle Z(s)=syslogfrac {\mathbf {Z}}{z_{11}}}}$

여기서₁₁ z는 Z의₁₁ 보완이고 Z는 [Z]의 행렬식이다.

위의 네트워크 예에서는

이 결과는 직렬 및 병렬로 보다 직접적인 저항 방법을 통해 쉽게 정확함을 검증할 수 있습니다.그러나 이러한 방법은 분석 대상 네트워크의 규모와 복잡성이 증가함에 따라 빠르게 지루하고 번거로워집니다.

[R], [L] 및 [D] 항목은 임의로 설정할 수 없습니다.[Z]가 임피던스 Z(s)를 실현하려면 [R], [L] 및 [D]가 모두 양의 정의 행렬이어야 합니다.그럼에도 불구하고, Z의 실현은 일반적으로 네트워크 내에 이상적인 변압기를 포함할 것입니다^{[note 5]}.상호 인덕턴스나 이상적인 변압기를 필요로 하지 않는 변압기만을 찾는 것은 더 어려운 작업입니다.마찬가지로 "다른 쪽 끝"에서 시작하여 Z에 대한 식을 지정하는 경우 다시 임의로 수행할 수 없습니다.합리적인 임피던스로 실현 가능하려면 Z(s)가 양의 실수여야 합니다.양의 현실(PR) 조건은 필요하고 충분하지만^[8] 일부 ^[7]토폴로지를 거부하는 실질적인 이유가 있을 수 있다.

[Z]의 특정 인스턴스에서 등가 합리적 1포트를 찾기 위한 일반적인 임피던스 변환은 빌헬름 코어에 의한 것입니다.실제 아핀 변환 그룹

$\displaystyle \mathbf {[Z']} = \mathbf {[T]} ^{T}\mathbf {[Z]} \mathbf {[T]} }$

어디에

${\displaystyle \mathbf {[T]} = cdots {bmatrix}1&0\cdots 0\\\T_{214}&T_{22}\cdots T_{2n}\\cdots &\cdots \\T_{n1}&T_{n2}\cdots T_{n}\end{bmatrix}}}$

는 Z 단위로 불변합니다.즉, 변환된 네트워크는 모두 여기서 설명한 정의에 따라 동등합니다.초기 소정의 매트릭스에 대한 Z(s)가 실현 가능한 경우, 즉 PR 조건을 충족하면 이 변환에 의해 생성된 모든 변환된 네트워크도 ^[7]PR 조건을 충족합니다.

3단자 및 4단자 네트워크

4단말기 네트워크에 대해 설명할 때 네트워크 분석은 실질적으로 유용한 광범위한 회로를 망라하는 2포트 네트워크의 관점에서 진행되는 경우가 많습니다.본질적으로 "2 포트"는 네트워크가 외부와 연결된 방식, 즉 단말기가 소스 또는 부하에 쌍으로 연결되어 있는 방식을 의미합니다.2 포트로 동작하지 않도록, 같은 네트워크를 사용해 외부 회로에 접속할 수 있습니다.이 아이디어는 그림 2에 나타나 있습니다.

3 터미널 네트워크는 2 포트로도 사용할 수 있습니다.이를 위해 한쪽 단말기가 양쪽 포트의 한쪽 단말기에 공통으로 접속됩니다.즉, 1개의 단말기가 2개의 단말기로 분할되어 네트워크가 사실상 4단말기 네트워크로 변환된 것입니다.이 토폴로지는 언밸런스토폴로지로 불리며 밸런스토폴로지와는 반대됩니다.밸런스 토폴로지에서는 그림 3을 참조하여 단자 1과 3 사이에서 측정된 임피던스가 2와 4 사이에서 측정된 임피던스와 같아야 합니다.이것은 포트를 형성하지 않는 단자 쌍입니다.포트를 형성하는 단자 쌍이 동일한 임피던스를 갖는 경우를 대칭이라고 합니다.엄밀히 말하면 밸런스 조건을 충족하지 않는 네트워크는 모두 언밸런스입니다만, 이 용어는 상기와 그림 3에 기재되어 있는3 터미널 토폴로지를 가리킵니다.불균형한 2포트 네트워크를 균형 잡힌 네트워크로 변환하는 것은 보통 매우 간단합니다.모든 시리즈 연결 요소가 반으로 분할되고 나머지 절반은 공통 브랜치로 재배치됩니다.대부분의 경우 역변환에서는 균형 토폴로지에서 불균형 토폴로지로 변환할 수 있지만 특정 토폴로지의 경우 이 방법으로 변환할 수 없습니다.예를 들어, 아래의 격자 변환에 대한 설명을 참조하십시오.

2 포트로 제한되지 않는3 터미널 네트워크 트랜스폼의 예로는 Y-Ω 트랜스폼이 있습니다.이는 동등한 임피던스를 찾기 위해 특히 중요한 변환입니다.그 중요성은 2개의 단말기 간의 총 임피던스를 특정 제한된 네트워크 클래스를 제외하고 직렬 및 병렬 조합을 계산하는 것만으로 결정할 수 없다는 사실에서 발생합니다.일반적인 경우 추가 변환이 필요합니다.Y-Ω 변환, 그 역 δ-Y 변환 및 이들 2개의 변환(스타 폴리곤 변환)의 n단자 아날로그는 일반적인 경우를 해결하기 위해 필요한 최소한의 추가 변환을 나타냅니다.직렬과 병렬은 사실 별과 폴리곤 위상의 2단자 버전입니다.직렬 및 병렬 조합으로 해결할 수 없는 일반적인 간단한 토폴로지는 브리지 네트워크에 대한 입력 임피던스입니다(브릿지의 ^[9]밸런스가 잡혀 있는 특수한 경우는 제외).이 섹션의 나머지 트랜스폼은 모두2 포트에서만 사용할 수 있도록 제한됩니다.

격자 변환

대칭 2포트 네트워크는 바틀렛의 이등분 정리를 사용하여 격자 네트워크로 변환할 수 있습니다.이 방법은 대칭 네트워크로 제한되지만 필터, 감쇠기 및 이퀄라이저에서 흔히 볼 수 있는 많은 토폴로지를 포함합니다.격자 토폴로지는 본질적으로 균형을 이루고 있으며, 격자에는 불균형 대응물이 없으며 일반적으로 변환된 네트워크보다 더 많은 구성요소를 필요로 합니다.

일부 공통 네트워크는 격자로 변환됩니다(X-networks).
묘사	네트워크	변환 방정식	변환된 네트워크
트랜스폼 3.1 T 네트워크를 격자 [10]네트워크로 변환합니다.		${\displaystyle Z_{\mathrm {A}}=Z_{1}\,\!}$ ${\displaystyle Z_{\mathrm {B}}=Z_{1}+2Z_{2}\!}$
트랜스폼 3.2 δ 네트워크를 격자 [10]네트워크로 변환합니다.		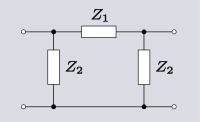${\displaystyle Z_{\mathrm {A} = flac {Z_{1}Z_{2}} {Z_{1}+2Z_{2}}\,\!}$ ${\displaystyle Z_{\mathrm {B}}=Z_{2}\ .}$
트랜스폼 3.3 브리지드 T 네트워크를 격자 네트워크로 [11]변환합니다.		${\displaystyle Z_{\mathrm {A} = flac {Z_{1}Z_{0} {Z_{1}+2Z_{0}}\,\!}$ ${\displaystyle Z_{\mathrm {B}}=Z_{0}+2Z_{2}\!}$

격자에서 불균형 위상으로 역변환하는 것은 패시브 성분의 관점에서 항상 가능한 것은 아닙니다.예를 들어 다음과 같은 변환이 있습니다.

묘사	네트워크	변환된 네트워크
Transform 3.4 격자 위상 이퀄라이저를 T [12]네트워크로 변환합니다.

변환된 회로에서 발생하는 음의 값으로 인해 패시브 구성 요소에서는 실현할 수 없습니다.단, 예를 들어 이 회로에서 상호 인덕턴스와 이상적인 변압기가 허용되면 실현될 수 있습니다.또 다른 방법은 회로 ^[13]구성 요소로 직접 음의 임피던스를 실현할 수 있는 능동 구성 요소를 사용할 수 있도록 하는 것입니다.

이러한 변환은 실제로 변환된 회선을 구축하는 목적이 아니라 원래 회선이 어떻게 동작하는지를 이해하는 데 도움이 될 수 있습니다.브리지드 T토폴로지의 다음 회선은 미드 시리즈m에서 파생된 필터 T섹션을 변경한 것입니다.이 회로는 적절한 값의 브리징 저항을 추가하면 션트 인덕터의 기생 저항이 제거된다고 주장하는 Hendrik Bode에 기인합니다.이 회로의 동작은 T 토폴로지로 변환되는 경우 분명합니다. 이 형태에서는 션트 분기에 음의 저항이 존재하며, 이는 ^[14]인덕터의 양의 기생 저항과 정확히 동일할 수 있습니다.

묘사	네트워크	변환된 네트워크
트랜스폼 3.5 브리지드 T 로패스필터 섹션의 T [14]섹션으로의 변환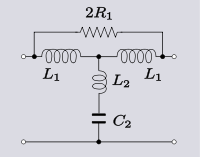

대칭 네트워크는 같은 방법으로 다른 대칭 네트워크로 변환할 수 있습니다.즉, 먼저 중간 격자 형식(위의 예에서 명확하게 하기 위해 생략)으로 변환하고 격자 형식에서 필요한 타깃 형식으로 변환합니다.예시와 마찬가지로 특별한 ^[15]경우를 제외하고 일반적으로 부정적인 요소가 발생합니다.

저항 제거

Sidney Darlington에 의한 정리에 따르면 PR 함수 Z는 정의 저항 R로 종단되는 무손실 2포트로서 실현될 수 있다.즉, 임피던스 네트워크를 나타내는 매트릭스[Z] 내의 저항의 수에 관계없이 출력 포트(통상 부하를 나타냄)에 1개의 저항만 있는 LC형 네트워크로서 네트워크를 완전히 실현하는 변환을 찾을 수 있습니다.지정된 응답을 실현하기 위해 네트워크 내 저항기는 필요하지 않습니다.따라서 출력 포트가 필요한 ^[8][16][17]값의 저항으로 종단되어 있는 경우 3 요소 종류의 2 포트 네트워크를 2 요소 종류의 2 포트 네트워크로 언제든지 축소할 수 있습니다.

이상적인 변압기 배제

이상적인 변압기 및 기타 임피던스 요소를 사용하여 수행할 수 있는 기본 변환은 임피던스를 변압기의 다른 쪽으로 이동하는 것입니다.다음 모든 변환에서 r은 변압기의 회전비입니다.

묘사	네트워크	변환된 네트워크
트랜스폼 4.1 강압 변압기를 통한 직렬 임피던스.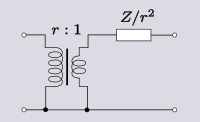
트랜스폼 4.2 강압 변압기를 통해 임피던스를 션트합니다.
트랜스폼 4.3 승압 변압기를 통해 분로 및 직렬 임피던스 네트워크.

이러한 변환은 단일 요소에만 적용되는 것이 아닙니다.네트워크 전체를 트랜스포머를 통과할 수 있습니다.이와 같이 하면, 네트워크상에서 변압기를 보다 편리한 장소로 이동할 수 있습니다.

Darlington은 이상적인 변압기를 완전히 제거할 수 있는 동등한 변압기를 제공합니다.이 기술을 사용하려면 변압기가 같은 종류의 임피던스를 가진 "L" 네트워크 옆에 있어야 합니다(또는 다음으로 이동할 수 있어야 합니다).모든 변형에서 변환은 "L" 네트워크가 반대 방향, 즉 위상적으로 미러링됩니다.^[2]

묘사	네트워크	변환된 네트워크
Transform 5.1 스텝다운 변압기 제거.
Transform 5.2 스텝업 변압기 제거
예 3 트랜스폼 5.1의 예.

예 3은 그 결과가 L-네트워크가 아닌 L-네트워크임을 나타내고 있습니다.그 이유는 션트 소자의 캐패시턴스가 변환에 필요한 용량보다 크기 때문에 변환 적용 후에도 일부 캐패시턴스가 남아 있기 때문입니다.초과가 대신 변압기에 가장 가까운 요소에서 발생한 경우, ^[2]변압기를 실행하기 전에 먼저 변압기의 다른 쪽으로 초과를 이동시킴으로써 이 문제를 처리할 수 있습니다.

용어.

레퍼런스

참고 문헌

• Bartlett, A. C., "인공선 특성 확장", Phil. 1927년 11월 제4권 902쪽
• Belvitch, V., "회로 이론의 역사 요약", IRE 제50권, Iss 5, 페이지 848-855, 1962년 5월.
• E. Cauer, W. Mathis 및 R. Pauli, "Wilhelm Cauer (1900 – 1945)", 제14회 네트워크 및 시스템 수학 이론 국제 심포지엄 진행, Perpignan, 2000년 6월.
• Foster, Ronald M.; Campbell, George A., Transactions of the American Electric Engineers, vol.39, isss.1, 페이지.230-290, 1920년 1월.
• Darlington, S., "저항기, 인덕터 및 콘덴서로 구성된 회로에 대한 네트워크 합성 및 필터 이론의 역사", IEEE Trans. 회로 및 시스템, vol 31, 페이지 3-13, 1984.
• Parago, P. S., An Introduction to Linear Network Analysis, The English Universities Press Ltd, 1961.
• Khan, Sameen Ahmed, "Farey sequence and resistive network", 인도과학아카데미(수학과학회), vol.122, issue.2, 페이지 153-162, 2012년 5월.
• 조벨, O.J.균일 및 복합 전파 필터의 이론 및 설계, 벨 시스템 기술 저널, 제2권(1923), 페이지 1-46.