실존 그래프

Existential graph
다음에 대한 시리즈 일부
찰스 샌더스 피어스
철학적
전기의

실존적 그래프는 논리적 표현에 대한 도식이나 시각적 표기법의 일종으로, 찰스 샌더스 피르스가 제안한 것으로, 일찍이 1882년에 그래픽 논리로 글을 썼으며,[1] 1914년에 사망할 때까지 이 방법을 계속 개발하였다.

그래프

Peirce는 실존적 그래프의 세 가지 시스템을 제안했다.

알파 둥지는 베타 및 감마. 베타는 Peirce에 의해 제시된 것보다 더 일반적인 수량화된 모달 논리인 감마선에 둥지를 틀지 않는다.

알파

알파 그래프

구문은 다음과 같다.

  • 빈 페이지;
  • 페이지의 아무 곳에나 쓰여진 단일 문자 또는 구문
  • 모든 그래프는 컷 또는 셉이라는 단순한 닫힌 곡선으로 둘러싸일 수 있다. 베인 상처는 비어 있을 수 있다. 베인 상처는 마음대로 둥지를 틀고 접합할 수 있지만 절대 교차해서는 안 된다.

그래프의 잘 형성된 부분은 모두 서브그래프다.

의미론은 다음과 같다.

  • 빈 페이지는 진리를 나타낸다.
  • 문자, 구문, 하위 그래프 및 전체 그래프는 참 또는 거짓일 수 있다.
  • 하위 그래프를 잘라낸 것으로 둘러싸는 것은 논리적 부정 또는 부울 보완과 같다. 따라서 빈 컷은 False를 의미한다.
  • 주어진 컷 안에 있는 모든 서브그래프는 암묵적으로 결합되어 있다.

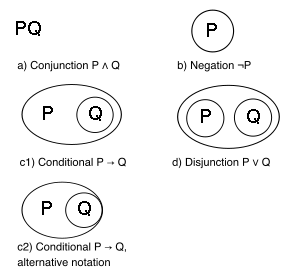
따라서 알파 그래프는 And and Not의 표현적 적절성에 기초하여 보초적 논리에 대한 최소주의 표기법이다. 알파 그래프는 2소 부울 대수와 진리 펑터의 급진적인 단순화를 구성한다.

물체의 깊이는 물체를 둘러싸는 절단 수입니다.

추론 규칙:

  • 삽입 - 모든 하위 그래프는 홀수 번호의 깊이로 삽입할 수 있다.
  • 삭제 - 짝수 깊이의 모든 하위 그래프는 지워질 수 있다.

동등성 규칙:

  • 이중 절단 - 아무 사이도 없는 한 쌍의 절단면이 어떤 서브그래프 주위로 그려질 수 있다. 마찬가지로 둘 사이에 아무 것도 없는 중첩된 두 개의 절개도 지워질 수 있다. 이 규칙은 부울 비자발성과 동등하다.
  • 반복/이중 – 이 규칙을 이해하려면 그래프를 노드와 조상이 있는 트리 구조로 보는 것이 가장 좋다. 노드 n의 서브그래프 P는 n에 따라 어떤 노드로도 복사할 수 있다. 마찬가지로, 노드 n의 하위 그래프 P는 어떤 노드 조상에 n(즉, n이 의존하는 노드)에 P의 복사본이 존재하는 경우 지워질 수 있다. 대수 컨텍스트에서 등가 규칙의 경우 형식 법칙의 C2를 참조하십시오.

증명은 위의 규칙 중 하나로 각 단계가 정당화된 일련의 단계에 의해 그래프를 조작한다. 빈 페이지나 빈 페이지까지 단계적으로 그래프를 축소할 수 있다면, 그것은 현재 tautology(또는 그 보완물)라고 불리는 것이다. 일정 지점 이상으로 단순화할 수 없는 그래프는 1차 로직의 만족스러운 공식과 유사하다.

베타.

직관적인 영어 구절을 사용하는 Peirce 공증식 술어; 현대 논리의 표준 표기법, 대문자 라틴 문자도 사용될 수 있다. 점은 담론의 영역에서 어떤 개인의 존재를 주장한다. 동일한 객체의 여러 인스턴스(instance)는 "identity의 선(line of identity)"이라고 하는 선으로 연결된다. 1차 논리라는 의미에서 문자 그대로의 변수나 정량자는 없다. 둘 이상의 술어를 연결하는 정체성의 선은 술어가 공통 변수를 공유한다고 주장하는 것으로 읽을 수 있다. 정체성의 선이 존재하려면 동등성의 알파 규칙을 수정해야 한다.

베타 그래프는 모든 변수가 암묵적으로 정량화되기 때문에 모든 공식을 닫힘으로 간주하는 시스템으로 읽을 수 있다. 정체성의 선의 "최악" 부분이 고른 (이상) 깊이를 갖는다면, 관련 변수는 암묵적으로 실존적으로 (범용적으로) 수량화된다.

제만(1964)은 베타 그래프가 동등성을 가진 1차 논리(Zeman 1967 참조)에 대해 이형적이라는 점에 가장 먼저 주목했다. 그러나 2차 문헌, 특히 로버츠(1973년)와 신(2002년)은 이것이 어떻게 그렇게 된 것인지에 대해서는 의견이 일치하지 않는다. 1928년 초판 데이비드 힐버트(David Hilbert)와 빌헬름 애커만의 수학논리 원리(Wilhelm Ackermann's Fronics of Mathematical Logic)에서 1차적 논리(Firce)가 먼저 명확하게 표현되었기 때문에, 페이스의 글은 이 질문을 다루지 않는다.

감마

알파 구문에 실선이 아닌 점선을 사용하여 작성된 두 번째 종류의 단순 닫힌 곡선을 추가한다. Peirce는 모달 로직의 원시적인 단항 연산자로 읽을 수 있는 이 두 번째 스타일의 컷에 대한 규칙을 제안했다.

제만(1964)은 감마 그래프 규칙의 간단한 수정이 잘 알려진 모달 로직 S4와 S5를 산출한다는 점에 가장 먼저 주목했다. 따라서 감마 그래프는 일반적인 모달 로직의 독특한 형태로 읽힐 수 있다. 제만의 발견은 오늘날까지 알려지지 않았지만, 그럼에도 불구하고 여기에 관심의 대상으로 포함된다.

페어스의 역할

실존적 그래프는 주요한 기호학의 창시자인 Peirce와 논리학자 Peirce의 호기심 많은 자손이다. Peirce의 그래픽 논리는 논리와 수학에서 그의 많은 업적 중 하나에 불과하다. 1867년에 시작되어 1885년 미국 수학 저널에 실린 그의 고전 논문으로 절정에 이른 일련의 논문에서, Peirce는 2개의 원소 부울 대수학, 명제 미적분학, 정량화와 술어적 미적분학, 그리고 몇몇 초보적인 세트 이론의 많은 부분을 발전시켰다. 모델 이론가들은 페어스를 가장 먼저 생각한다. 그는 또한 드 모건의 관계 대수학을 연장했다. 그는 메탈로지컬이 부족했다.

그러나 페어스의 진화하는 기호학적 이론은 그가 전통적인 선형 표기법을 사용하여 공식화한 논리의 가치를 의심하게 만들었고, 논리학과 수학은 2차원(또는 심지어 3차원)으로 공증되는 것을 선호하게 했다. 그의 작품은 오일러의 도표와 벤의 1880년 개정판을 뛰어넘었다. 프레지의 1879년 베그리프슈흐리프트도 논리에 2차원 표기법을 사용했지만, 하나는 페이스의 표기법과는 매우 다르다.

Peirce가 최초로 발행한 그래픽 논리학 논문(His Collected Papers의 제3권에 다시 게재됨)은 (실제로는) 알파 실존적 그래프에 대한 시스템 이중(실제적으로)을 제안했는데, 이 그래프는 '귀속적 그래프'라고 불린다. 그는 곧 실존적 그래프에 유리하게 이 형식주의를 버렸다. 1911년 빅토리아 여왕은 실존적 그래프를 C. K. Ogden에게 보여주었는데, 그는 이 그래프를 "덜 난해한 형태"로 Welby의 생각과 유용하게 결합될 수 있다고 느꼈다.[2] 그렇지 않으면 그들은 그의 생애 동안 거의 관심을 끌지 못했고 로버츠(1964년)와 제만(1964년)에 의해 박사학위 논문까지 그의 죽음 이후 변함없이 폄하되거나 무시당했다.

참고 항목

참조

  1. ^ Peirce, C. S. "[논리의 정크쳐와 골절들] (MS 427 (새로운 번호 부여 시스템), Fall–Winter 1882), 그리고 찰스 S의 저술인 "Peirce to O. H. Mitchell" (1882년 12월 21일, L. 294년 12월 21일), Peirce, v. 4, 393페이지(Google Preview)의 "Junctures"와 394-399페이지(Google Preview)의 글자(Google Preview. Sowa, John F. (1997), "언어 구조와 논리적 구조를 일치시키는 것"을 참조하라, 찰스 샌더스 피어스, 네이선 하우저, 돈 D. 로버츠, 그리고 제임스 반 에브라, 블루밍턴과 인디애나폴리스의 편집자: 인디애나 대학 출판부 418-4444쪽 420, 425, 426, 428 참조.
  2. ^ Petrilli, Susan (2017). Victoria Welby and the Science of Signs: Significs, Semiotics, Philosophy of Language. Routledge. ISBN 978-1-351-29598-7.

추가 읽기

제1차 문헌

  • 1931–1935 & 1958. 찰스 샌더스 피르스의 논문집. 제4권 제2권: "실존 그래프"는 문단 347~584로 구성되어 있다. 617항에서도 논의가 시작된다.
    • 문단 347~349(II.1.1 "논리적 다이어그램")—볼드윈의 철학 및 심리학 사전(1902) v. 2, 페이지 28에서 피어의 정의 "논리적 다이어그램(또는 그래프)" 심리학사 에프린트의 고전.
    • 350~371항 (II.1.2. "오일러 도표")—"그래프"(설명서 479) c. 1903.
    • 문단 372~584 Eprint.
    • 문단 372~393(II.2. "기호 논리")—Peirce's part of "Symbolic Logic" in Baldwin's Dictionary of Philosophy and Psychology (1902) v. 2, pp. 645–650, beginning (near second column's top) with "If symbolic logic be defined...". Paragraph 393 (Baldwin's DPP2 p. 650) is by Peirce and Christine Ladd-Franklin ("C.S.P., C.L.F.").
    • 394–417항 (II.3. "존재 그래프")—페어스의 소책자, 페이지 15–23, 알프레드 머지 & 손, 보스턴(1903)에서 인용.
    • 문단 418~509(II.4. "실존적 그래프, 오일러의 도표 및 논리 대수")—"논리학적 그래프, 2번" (기호 492), c. 1903".
    • 510~529항 (II.5. "실존 그래프의 감마 부분")—"로웰 강의", 렉처 IV(설명서 467)의 단락.
    • 단락 530–572 (II.6)—"실용주의에 대한 사과에 대한 프로레고메나"(1906), 더 모니스트, v. 16세, n. 4, 페이지 492-546. 《Monist v. XVII》의 수정 (1907) 페이지.
    • 573~584항 (II.7. "감마 그래프의 개선")—"국립과학아카데미, 1906년 4월 워싱턴 회의"(설명서 490)의 단락.
    • 제617~623항(최소한 (제3권, 제2장, 제2장, 제2항, 제594~642호)—"어메이징 메이즈: 호기심 더 퍼스트의 설명", 모니스트, v. 16II, 1908, n. 3, 페이지 416-4644는 시작 페이지 440을 참조한다.
  • 1992. "렉처 3: 친척의 논리", 추리 그리고 사물의 논리, 페이지 146–164. 케트너, 케네스 레인(편집과 서론), 힐러리 푸트남(해설사). 하버드 대학 출판부. 1898년 매사추세츠 캠브리지에서 열린 Peirce의 강의.
  • 1977, 2001. 기호 및 의미: C.S. 간의 통신 피어스와 빅토리아 레이디 웰비. C.S. 하드윅, 에드. 러벅 TX: 텍사스 공대 프레스. 2001년 2판.
  • Peirce의 MS 514(1909년)의 필사본으로, John Sawa의 해설을 곁들여 편집했다.

현재, Peirce의 작품들의 연대기적 비평판인 Writishs는 1892년까지 밖에 확장되지 않는다. Peirce의 논리 그래프에 대한 많은 작품들은 그 날짜 이후에 쓰여진 원고로 이루어져 있고, 여전히 출판되지 않았다. 따라서 Peirce의 그래픽 논리에 대한 우리의 이해는 연대기 판의 나머지 23권이 나타나면서 바뀔 것 같다.

제2차 문헌

  • 해머, 에릭 M. (1998), "실존적 그래프를 위한 반석학", 철학 논리학 저널 27: 489–503.
  • 케트너, 케네스 레인
    • (1981), 미국 기호학 저널 대 I, n. 1–2, 페이지 47–83의 "반증 및 반증 치료의 최선의 예 및 그 사용". 기사는 실존적 그래프를 소개하는 것이다.
    • (1990), 논리의 요소: Peirce의 실존적 그래프 소개, 텍사스 공대 출판사, 러벅, TX, 99페이지, 나선형 바인딩.
  • 케이로스, 주앙 & 스텐펠트, 프레데릭
    • (2011), "직교적 추론과 페이르체안 논리 표현", 세미오티카 제186권 (1/4) (페르체 도식 논리에 관한 특별호) [1]
  • 로버츠, 돈 D
    • (1964), E. C. 무어의 "존재 그래프와 자연 추론"과 로빈, R. S, 에드, C. S. Peirce의 철학 연구, 2번째 시리즈. Amherst MA: 매사추세츠 대학교 출판부. 퍼스의 그래픽 논리에 대해 어떠한 공감과 이해를 보여주는 첫 번째 간행물.
    • (1973. C.S.의 실존적 그래프. 파이르스. 존 벤자민 1963년 논문의 결과야
  • 신, 선주(2002년), Peirce's Graphs의 상징적 논리. MIT 프레스
  • 잘라메아, 페르난도 페어스의 연속성 논리. 2012년 보스턴 도슨트 프레스 ISBN 9 780983 700494.
    • 제2부: Peirce의 실존적 그래프, 76-162페이지.
  • 제만, J.J.

외부 링크