조명 문제
Illumination problem조명 문제는 점 광원에 의해 거울로 된 벽이 있는 방의 조명을 연구하는 수학적 문제의 한 종류다.
원래의 제형은 1950년대에 에른스트 스트라우스에게 귀속되어 해결되었다.[1]스트라우스는 거울에 비친 벽이 있는 방은 거울로 비친 벽에서 빛을 반복적으로 반사할 수 있는 단일 지점 광원으로 항상 조명할 수 있는지 물었다.또는 당구대를 어떤 필요한 모양으로 만들 수 있느냐는 질문으로 표현할 수 있는데, 공이 포인트처럼 되어 마찰로 인해 멈추기보다는 무한히 지속된다고 가정하면 다른 지점에서 당구공이 불가능한 지점이 있을 수 있는 형태가 있는가라고 할 수 있다.
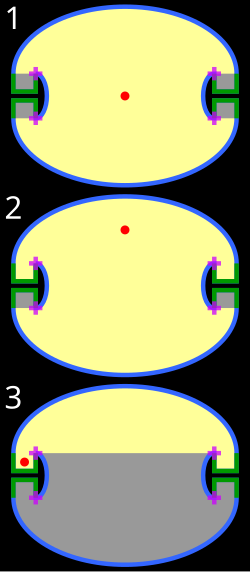
원래의 문제는 1958년 로저 펜로즈가 타원을 사용하여 펜로즈 불감증 방을 형성함으로써 처음 해결되었다.[1]그는 단일 점원으로만 조명이 켜지면 항상 어두운 영역을 가져야 하는 곡선 벽이 있는 방이 존재한다는 것을 보여주었다.이 문제는 1995년 조지 토카르스키에 의해 2차원과 3차원에 대한 폴리곤실에서도 해결되었는데, 이것은 방의 다른 지점에서 조명을 받지 않는 "어두운 점"이 있는, 불분명한 폴리곤실 26면 방이 존재한다는 것을 보여 주었고, 심지어 반복적인 반사가 가능했다.[2]이러한 경우는 드물지만, (지역이 아닌) 한정된 수의 암점이 포인트 소스의 고정된 위치에서만 발광할 수 없는 경우였다.1997년, 같은 성질의 24면 두 개의 다른 방들이 조지 토카스키와 데이비드 카스트로에 의해 별도로 제시되었다.[3][4]
1995년 토카르스키는 4면과 2개의 고정된 경계점을 가진 최초의 폴리곤 불연성 방을 발견했다.[5]2016년 릴리에브르, 몬테일, 와이스는 각도(도 단위)가 모두 이성적인 숫자인 폴리곤실의 광원이 유한한 수의 점을 제외하고 전체 폴리곤을 비춘다는 것을 보여주었다.[6]
참조
- ^ a b Weisstein, Eric W. "Illumination Problem". Wolfram Research. Retrieved 19 December 2010.
- ^ Tokarsky, George (December 1995). "Polygonal Rooms Not Illuminable from Every Point". American Mathematical Monthly. University of Alberta, Edmonton, Alberta, Canada: Mathematical Association of America. 102 (10): 867–879. doi:10.2307/2975263. JSTOR 2975263.
- ^ Castro, David (January–February 1997). "Corrections" (PDF). Quantum Magazine. Washington DC: Springer-Verlag. 7 (3): 42.
- ^ Tokarsky, G.W. (February 1997). "Feedback, Mathematical Recreations". Scientific American. New York, N.Y.: Scientific American, Inc. 276 (2): 98. JSTOR 24993618.
- ^ Tokarsky, G. (March 1995). "An Impossible Pool Shot?". SIAM Review. Philadelphia, PA: Society for Industrial and Applied Mathematics. 37 (1): 107–109. doi:10.1137/1037016.
- ^ Lelièvre, Samuel; Monteil, Thierry; Weiss, Barak (4 July 2016). "Everything is illuminated". Geometry & Topology. 20 (3): 1737–1762. arXiv:1407.2975. doi:10.2140/gt.2016.20.1737.