영향선

공학에서, 영향력 선은 구조물을 따라 임의의 지점에 배치된 단위 하중에 의해 발생하는 빔 또는 트러스의 특정 지점에서의 함수(구조 부재에서 느껴지는 전단, 모멘트 등)의 변동을 그래프로 표시한다.^{[1][2][3][4][5]} 영향선과 함께 연구되는 공통 기능으로는 반응(구조물의 지지대가 정적인 상태를 유지하기 위해 적용되어야 함), 전단, 모멘트, 편향(변형) 등이 있다.^[6] 영향선은 교량, 크레인 레일, 컨베이어 벨트, 바닥 거더 및 하중이 그 경간을 따라 이동하는 기타 구조물에 사용되는 보와 트러스를 설계하는 데 중요하다.^[5] 영향선은 하중이 연구된 기능 중 어떤 것에 대한 최대 효과를 발생시키는 위치를 보여준다.

영향선은 스칼라와 첨가물이다.^[5] 즉, 적용될 하중이 단위 하중이 아니거나 복수의 하중이 가해지는 경우에도 사용할 수 있다. 구조물에 대한 비단위 하중의 영향을 찾기 위해, 영향선으로 얻은 서수체 결과에 적용할 실제 하중의 크기를 곱한다. 전체 영향선을 확대하거나 또는 선을 따라 경험하는 최대 및 최소 효과만 조정할 수 있다. 최대 및 최소 스케일 크기는 빔 또는 트러스에서 설계해야 하는 임계 크기입니다.

복수 하중이 적용될 수 있는 경우, 구조물이 특정 지점에서 느끼는 총 효과를 얻기 위해 개별 하중에 대한 영향선을 함께 추가할 수 있다. 영향선을 함께 추가할 때는 구조물의 하중의 간격에 따라 적절한 오프셋을 포함시킬 필요가 있다. 예를 들어, 트럭 하중이 구조물에 적용된다. 후면 차축 B는 전면 차축 A보다 3피트 뒤쪽에 있고, 그 다음 구조물을 따라 x피트(x – 3)피트(b)에서 A의 효과를 더해야 한다. 구조물을 따라 x피트(b)에서 b의 효과를 더해야 한다. 구조물을 따라 x피트(x – 3)피트(b)에서 B의 효과를 더해야 한다.

많은 하중이 집중되기보다는 분산된다. 영향선은 집중 또는 분산 하중과 함께 사용할 수 있다. 집중(또는 점) 하중의 경우, 단위 하중은 구조물을 따라 이동한다. 주어진 폭의 분산하중의 경우, 하중이 끝단에 가까워지고 구조물을 벗어나면 전체 하중의 일부만 구조물에 의해 운반된다는 점에 유의하여 동일한 폭의 단위 분산하중을 구조물을 따라 이동시킨다. 분산 장치 하중의 영향은 또한 구조물의 해당 길이에 대한 점 하중의 영향선을 통합함으로써 얻을 수 있다.

결정 구조물의 영향선은 메커니즘이 되는 반면, 불확실한 구조물의 영향선은 단지 결정된다.^[7]

베티의 정리로부터의 데모

영향선은 베티의 정리를 바탕으로 한다. From there, consider two external force systems, ${\displaystyle F_{i}^{P}}$ and ${\displaystyle F_{i}^{Q}}$, each one associated with a displacement field whose displacements measured in the force's point of application are represented by ${\displaystyle d_{i}^{P}}$ and ${\di$$splaystyle d_{i}^{Q$ .

$F{\displaystyle {}_{}^{}}$ ${\displaystyle i_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$ 시스템이$$ 평형 상태에 있는 구조에 가해지는 실제 힘을 나타낸다고 간주한다. Consider that the ${\displaystyle F_{i}^{Q}}$ system is formed by a single force, ${\displaystyle F^{Q}}$. The displacement field ${\displaystyle d_{i}^{Q}}$ associated with this forced is defined by releasing the structural restraints acting on the point where ${\displaystyle F^{Q}}$$$ d ${\displaystyle {1\mathrm{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$=${\displaystyle }$- 1 ${\displaystyle d_{1}^{Q}=-1}$로 표현되는 음의 방향으로 동적으로 허용되는 상대 단위 변위를 적용하고 부과한다$.$베티의 정리로부터 다음과 같은 결과를 얻는다.

${\displaystyle -F_{1}^{P}+\sum _{i=2}^{n_{i}^{P}d_{i}^{Q}=F^{Q}\times 0\iffF_{1}^{P}=\sum _{i=2}^{n}F_{i}^{P}d_{i}^{Q}}}}}}}}$

개념

빔 또는 트러스 설계 시 구조물의 수명 동안 구성원이 고장나지 않도록 구조 부재 내에서 최대 기대 반응, 피복 및 모멘트를 유발하는 시나리오를 설계할 필요가 있다. 사하중(구조물 자체의 중량 등 절대 움직이지 않는 하중)을 처리할 때는 하중을 예측하고 계획하기 쉽기 때문에 비교적 쉽다. 활하중(가구 및 사람 등 구조물의 수명 동안 이동하는 모든 하중)의 경우, 하중이 어디에 있는지 또는 구조물의 수명 동안 얼마나 집중되거나 분포될 것인지를 예측하기가 훨씬 어려워진다.

영향선은 단위 부하가 빔 또는 트러스 위를 이동할 때 빔 또는 트러스 반응을 그래프로 표시한다. 영향선은 설계자가 반응, 전단 또는 모멘트 각 기능에 대한 최대 결과 반응을 계산하기 위해 활하중을 배치할 위치를 찾는 데 도움이 된다. 그런 다음 설계자는 빔 또는 트러스 설계가 필요한 각 기능의 최대 응답을 계산하기 위해 최대 예상 부하로 영향선을 조정할 수 있다. 영향선은 또한 적용된 장치 부하에 대한 다른 기능(편향 또는 축력 등)의 반응을 찾는 데 사용될 수 있지만, 이러한 영향선의 사용은 덜 일반적이다.

영향선 구성 방법

영향선 건설에는 세 가지 방법이 사용된다. 첫 번째는 구조물을 따라 여러 점에 대한 영향 값을 표로 작성한 다음, 해당 점을 사용하여 영향선을 작성한다.^[5] 두 번째는 구조물에 적용되는 영향선 방정식을 결정하여 x의 관점에서 영향선을 따라 모든 점에 대해 해결하는데, 여기서 x는 구조물의 시작점에서 단위 하중이 적용되는 지점까지의 피트 수입니다.^{[1][2][3][4][5]} 세 번째 방법은 뮐러브레슬라우의 원리라고 한다. 그것은 질적인 영향선을 만든다.^[1][2][5] 이 영향선은 여전히 설계자에게 단위 부하가 연구 중인 지점에서 함수의 가장 큰 반응을 생성하는 위치를 정확하게 파악할 수 있지만, 처음 두 방법에 의해 생성된 영향선은 그 반응이 얼마나 큰지 계산하는 데 직접 사용할 수는 없다.

값 표 작성

구조물의 특정 지점 A에 대한 영향 값을 표로 작성하려면 구조물을 따라 다양한 지점에 단위 하중을 배치해야 한다. 통계학은 A 지점에서 함수의 값(반작용, 전단 또는 순간)을 계산하는 데 사용된다. 일반적으로 상향 반응은 양성으로 보인다. 전단 및 모멘트는 전단 다이어그램과 모멘트 다이어그램에 사용되는 동일한 규칙에 따라 양수 또는 음수 값이 주어진다.

R. C. Hibbeler는 그의 저서 Structural Analysis에서 "정적으로 결정되는 모든 빔은 직선 세그먼트로 구성된 영향선을 가질 것이다."^[5]라고 말한다. 따라서 영향선의 기울기에 변화를 일으킬 점을 인식하고 그 지점에서의 값만 계산하면 계산 횟수를 최소화할 수 있다. 변곡선의 기울기는 지지대, 중간 스판 및 이음매에서 변경할 수 있다.

반응, 축력, 전단력 또는 휨모멘트와 같은 특정 기능에 대한 영향선은 구조물의 어떤 지점에서 단위 하중이 적용되기 때문에 구조물의 특정 지점에서 해당 기능의 변동을 보여주는 그래프다.

함수에 대한 영향선은 전단, 축 또는 휨 모멘트 다이어그램과 다르다. 영향선은 구조물의 여러 지점에서 단위 하중을 독립적으로 적용하고 원하는 위치에서 전단, 축 및 모멘트 등 이 하중에 의한 함수 값을 결정함으로써 생성될 수 있다. 그런 다음 각 함수에 대해 계산된 값을 하중이 가해진 위치에 표시한 다음 함수에 대한 영향선을 생성한다.

영향력 값을 표로 작성했으면, A 지점의 함수에 대한 영향선을 x 단위로 그릴 수 있다. 먼저 표로 표시된 값을 찾아야 한다. 표로 표시된 지점 사이의 섹션에 대해서는 보간이 필요하다. 따라서 점을 연결하기 위해 직선을 그릴 수 있다. 일단 이것이 이루어지면 영향선은 완성된다.

영향선 방정식

구조물의 전체 범위에 걸쳐 영향선을 정의하는 방정식을 만들 수 있다. 이는 특정 거리가 아닌 구조물을 따라 x 피트에 배치된 단위 하중에 의해 야기되는 A 지점에서의 반응, 전단 또는 모멘트에 대한 해결을 통해 이루어진다. 이 방법은 표로 나타낸 값법과 비슷하지만, 숫자 솔루션을 얻기보다는 x의 관점에서 그 결과가 방정식이다.^[5]

영향선의 선형 섹션마다 영향선 방정식이 변경되기 때문에 이 방법에 대해 영향선의 기울기가 변경되는 위치를 이해하는 것이 중요하다. 따라서 완전한 방정식은 영향선의 각 선형 섹션에 대해 별도의 영향선 방정식을 갖는 조각형 선형함수다.^[5]

뮐러브레슬라우의 원리

뮌헨닷컴에 따르면 뮐러-브레슬라우 원칙은 실제 영향력 라인에 정비례하는 질적 영향력 라인을 그리는 데 활용할 수 있다.^[2] 뮐러-브레슬라우 원리는 빔을 따라 단위 하중을 이동하는 대신, 연구 중인 지점에서 빔을 먼저 해제한 다음, 그 지점에 연구 중인 기능(반응, 전단 또는 모멘트)을 적용함으로써 발생하는 빔의 편향된 형상을 찾아낸다. 원리는 함수의 영향선이 함수에 의해 작용했을 때 빔의 굴절된 모양과 같은 스케일링 형상을 갖는다고 말한다.

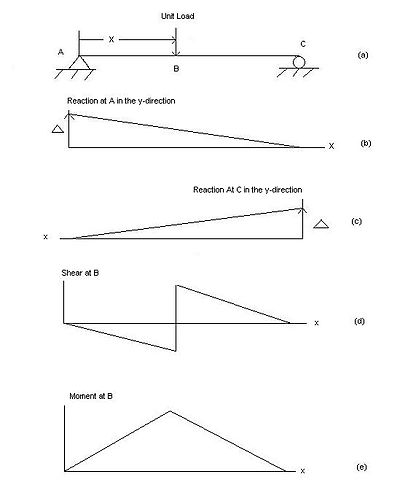
빔이 기능 아래에서 어떻게 꺾이는지를 이해하려면, 기능에 저항할 수 있는 빔의 용량을 제거해야 한다. 아래는 단순하게 지지되는 강체 빔의 영향선을 찾는 방법에 대한 설명이다(그림 1에 표시된 것과 같은 것).

• 지지대에서 발생하는 반응을 판단할 때 지지대는 수직 반응을 거부할 수 없는 롤러로 대체된다.^[2][5] 그런 다음 지지도가 있었던 지점에 상향(긍정적) 반응이 적용된다. 지지대가 제거되었기 때문에 빔은 위쪽으로 회전하며, 빔은 경직되기 때문에 두 번째 지지대에 점이 있는 삼각형을 만든다. 빔이 캔틸레버로서 두 번째 지지대 이상으로 확장되는 경우, 캔틸레버 위치 아래에 유사한 삼각형이 형성될 것이다. 이는 반작용의 영향선이 두 번째 지지대가 위치한 위치에서 값이 0인 직선 경사진 선이 된다는 것을 의미한다.

• 빔을 따라 B 지점에서 발생한 전단 결정 시 빔을 절단하고 B 지점에 롤러 가이드(모멘트에 저항할 수 있지만 전단에는 저항할 수 없는 것)를 삽입해야 한다.^[2][5] 그러면 그 지점에 양전단을 가함으로써 왼쪽이 아래로 회전하지만 오른쪽이 위로 회전하는 것을 알 수 있다. 이것은 지지대에서 0에 도달하고 그 기울기가 불연속성의 양쪽에 동일한 불연속 영향선을 만든다. 점 B가 지지대에 있으면 점 B와 다른 지지대 사이의 편향은 여전히 삼각형을 만들지만, 만약 빔이 칸틸레버버로 되어 있다면, 칸틸레버 쪽 전체가 직사각형을 만들어 위아래로 움직인다.

• 빔을 따라 B 지점에서 발생한 모멘트를 결정할 때 힌지는 B 지점에 배치되어 모멘트로 해제되지만 전단에는 저항한다.^[2][5] 그런 다음 포지티브 모멘트가 B 지점에 배치되면 빔의 양쪽이 위로 회전한다. 이렇게 하면 연속적인 영향선이 생성되지만 경사도는 B 지점의 힌지 양쪽에서 동일하고 반대쪽이 된다. 빔은 단순 지지되기 때문에 엔드 지지대(핀)는 모멘트에 저항할 수 없으므로, 하중이 어디에 놓이든지 정적 상황에서 결코 모멘트를 경험하지 못한다는 것을 알 수 있다.

뮐러-브레슬라우 원리는 질적 영향선만 생산할 수 있다.^[2][5] 즉, 엔지니어는 이를 사용하여 최대 함수를 발생시키기 위해 하중을 배치할 위치를 결정할 수 있지만, 그 최대값의 크기는 영향력 라인에서 계산할 수 없다. 대신 엔지니어는 로딩 케이스의 함수 값에 대한 문제를 해결하기 위해 통계학을 사용해야 한다.

대체 적재 케이스

다중 하중

가장 간단한 하중 케이스는 단일 점 하중이지만, 여러 하중과 분산 하중으로 인한 반응을 결정하는 데 영향선을 사용할 수도 있다. 때로는 일정한 거리를 두고 여러 개의 하중이 발생하는 것으로 알려져 있다. 예를 들어, 다리 위에서 자동차나 트럭의 바퀴는 비교적 표준 거리에서 작용하는 점 하중을 생성한다.

영향선을 사용하여 이러한 모든 점 하중에 대한 함수의 반응을 계산하기 위해, 영향선과 함께 발견된 결과를 각 하중에 대해 스케일링할 수 있으며, 그 다음 스케일링된 크기를 합산하여 구조물이 견뎌야 하는 총 응답을 찾을 수 있다.^[5] 점하중은 그 자체로 크기가 다를 수 있지만, 구조물에 동일한 힘을 가하더라도 구조물을 따라 다른 거리에서 작용하기 때문에 별도로 스케일링할 필요가 있을 것이다. 예를 들어, 자동차의 바퀴가 10피트 떨어져 있는 경우, 첫 번째 세트가 다리 위 13피트일 때, 두 번째 세트는 다리 위 3피트일 뿐이다. 첫 번째 바퀴 세트가 다리에서 7피트 높이면 두 번째 세트가 아직 다리에 도달하지 못했기 때문에 첫 번째 세트만 다리에 하중을 가하는 것이다.

또한, 두 하중 사이에 하나의 하중이 더 무거운 경우, 최대 하중이 발견되었는지 확인하기 위해 두 하중 순서(오른쪽에 더 큰 하중이, 왼쪽에는 더 큰 하중)에서 하중을 검사해야 한다. 하중이 3개 이상일 경우 검사해야 할 경우의 수가 증가한다.

분산하중

많은 하중이 점 하중으로 작용하지 않고, 대신 확장된 길이 또는 면적에 걸쳐 분산 하중으로 작용한다. 예를 들어, 연속 트랙터가 있는 트랙터는 각 트랙의 길이에 분산된 하중을 가한다.

분산 하중의 효과를 찾기 위해 설계자는 구조물의 영향을 받는 거리에 걸쳐 점 하중을 사용하여 찾은 영향선을 통합할 수 있다.^[5] 예를 들어, 3피트 길이의 트랙이 빔을 따라 5피트에서 8피트 사이에 작용하는 경우, 그 빔의 영향선은 5피트에서 8피트 사이에 통합되어야 한다. 영향선의 통합은 분산 부하가 단위 크기를 가질 경우 느낄 수 있는 효과를 제공한다. 따라서 통합 후에도 설계자는 분산 로드의 실제 효과를 얻기 위해 결과의 크기를 조정해야 한다.

미확정 구조물

(위에서 언급한 바와 같이) 정적으로 결정되는 구조물의 영향선은 직선 세그먼트로 구성되지만, 불확실한 구조물의 경우는 동일하지 않다. 불확실한 구조물은 경직된 것으로 간주되지 않는다. 따라서, 구조물에 대해 그려진 영향선은 직선이 아니라 곡선일 것이다. 위의 방법들은 여전히 구조물의 영향선을 결정하는 데 사용될 수 있지만 빔 자체의 특성을 고려해야 하기 때문에 작업은 훨씬 더 복잡해진다.

참고 항목

• 빔
• 전단 및 모멘트 다이어그램
• 데드 및 활하중
• 뮐러브레슬라우의 원리

참조