주입물체
Injective object수학에서, 특히 범주 이론 분야에서, 주입 대상의 개념은 주입 모듈 개념의 일반화다.이 개념은 코호몰로지, 호모토피 이론, 모델 카테고리 이론에서 중요하다.이중 개념은 투영적인 물체의 개념이다.
정의
An object in a category is said to be injective if for every monomorphism and every morphism there exists a morphism 에 g {\displaystyle g를) 예: = g 로 확장.
즉, 모든 X→ 인자를 통해 모든 단일 형태론 X
위의 정의에서 형태론 은(는) 및 에 의해 고유하게 결정될 필요는 없다
로컬 소규모 범주에서 홈 펑터 C(- , ){\이(가) {\의 단일 형상을 과부하 세트 맵에 전달하도록 요구하는 것과 동등하다.
아벨 범주에서
주입성의 개념은 아벨리아 범주에 대해 처음 공식화되었으며, 이것은 여전히 주요 적용 분야 중 하나이다.C 이(가) 아벨 범주인 경우 의 개체 Q는 홈 펑터 HomC(–,Q)이 정확한 경우에만 주입된다.
→ → → V → → 0 0의 순서가 Q가 주입식인 처럼 C {C의 순서라면 시퀀스가 분할된다
충분한 주입 및 주입 선체
범주 은(는 의 모든 개체 X에 대해 X에서 주입 개체에 이르는 단형성이 존재한다면 충분한 주입물을 가지고 있다고 한다.
에서 단형성 g를 본질적인 단형성이라고 하는데, 만약 어떤 형태주의 f에 대해서, 복합 fg는 단형성인 경우에만 단형성이라고 한다.
만약 g가 도메인 X와 주입식 코도메인 G를 가진 필수적인 단성형이라면, G를 X의 주입식 선체라고 부른다.그런 다음 주입식 선체는 X에 의해 비수평적 이형성까지 독특하게 결정된다.
예
- 아벨 그룹과 그룹 동형성의 범주, Ab에서 주사 물체는 반드시 분리할 수 있는 집단이다.선택의 공리를 가정하면, 그 개념들은 동등하다.
- (왼쪽)모듈과 모듈 동형성, R-Mod 범주에서 주입 물체는 주입 모듈이다.R-Mod는 주입형 선체를 가지고 있다. 따라서 R-Mod는 충분한 주입을 가지고 있다.
- 미터법 공간인 메트(Met) 범주에서 주입형 물체는 주입형 미터법 공간이며, 미터법 공간의 주입형 선체는 그 좁은 공간이다.
- T0 공간과 연속 매핑 범주에서 주입 물체는 항상 연속 격자 위의 Scott 위상이며, 따라서 항상 냉정하고 국소적으로 압축된다.
사용하다
만약 아벨리아 범주에 충분한 주입이 있다면, 우리는 주입 분해능을 형성할 수 있다. 즉, 주어진 물체 X에 대해 우리는 긴 정확한 순서를 형성할 수 있다.
그런 다음 F를 이 시퀀스에 적용하고 결과(정확한 것은 아님) 시퀀스의 호몰로지를 계산하여 주어진 functor F의 파생 펑터를 정의할 수 있다.이 접근방식은 Ext, Tor functors 및 그룹 이론, 대수 위상 및 대수 기하학에서 다양한 코호몰로지 이론을 정의하는 데 사용된다.일반적으로 사용되는 범주는 일부 링된 공간(XX, O) 또는 보다 일반적으로 Grotendieck 범주에 걸쳐 Functor 범주 또는 O 모듈X 조각 범주다.
일반화
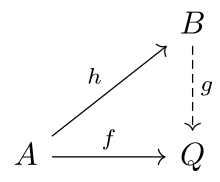
를) 범주로 하고 을(를) 의 모피즘 클래스로 한다
의 Q 은(는) injective라고 한다(모든 형태주의 : → Q 및 모든 형태론 → B 의 B에는 형태론 : → Q = 을를) 사용하는 B
H{\{\이 단형성의 등급이라면, 우리는 위에서 다루었던 주입 물체로 되돌아간다.
The category is said to have enough -injectives if for every object X of , there exists an -morphism from X to an -injective object.
A -morphism g in is called -essential if for any morphism f, the composite fg is in only if f is in .
g가 도메인 X와 H {\인 필수 형태론인 , G를 injective codomain G라고 한다.
H 삽입 객체의 예
- 단순 집합 범주에서, 아오디네 확장자의 H {\에 대한 주입 물체는 Kan complex이다.
- 부분적으로 주문한 세트와 모노톤 맵의 범주에서 완전한 격자는 주문-임베딩의 H 에 대한 주입 물체를 형성하며, 부분적으로 주문한 세트의 Dedekind-MacNeille 완성은 incal}주입체 선체이다.
참고 항목
메모들
참조
- J. 로지키, 주입성 및 접근성 범주
- F. 칼리아리와 S.몬토바니, T반사 및 섬유공간의0 주입 선체








 확장.
확장.




 순서가 Q가 주입식인
순서가 Q가 주입식인