켈리 기준

확률론에서 켈리 기준(또는 켈리 전략이나 켈리 내기)은 내기에 대한 최적의 이론적 크기를 결정하는 공식이다. 예상 수익이 알려졌을 때 유효하다. 켈리 베팅 크기는 예상되는 기하급수적 성장률을 극대화하는 것과 맞먹는 부의 로그의 기대치를 극대화해 찾아낸다. 1956년 벨 연구소의 연구원인 J. L. Kelly Jr.에 의해 설명되었다.^[1] 이 기준은 장기적으로 어떤 다른 전략(즉, 베팅 횟수가 무한대로 갈 때 이론적으로 최대 수익률)에 비해 높은 부를 이끌어 내기 때문에 과학적 도박법으로도 알려져 있다.

이^[2][3] 공식이 도박에 실용적으로 사용된다는 것이 입증되었고 투자 운용의 다양화를 설명하는데도 같은 생각을 사용하였다.^[4] 2000년대 들어 켈리식 분석이 주류 투자이론의^[5] 한 부분이 됐고 워런 버핏^[6], 빌 그로스^[7] 등 유명 성공투자자들이 켈리 방식을 사용한다는 주장이 제기됐다. 윌리엄 파운드스톤은 켈리 베팅의 역사에 대해 널리 알려진 이야기를 썼다.^[8] 또한 임시 포트폴리오 선택을 참조하십시오.

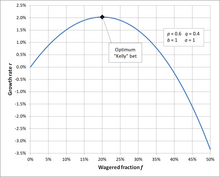
최적 베팅 사례

한 연구에서, 각 참가자들에게 25달러가 주어졌고, 60퍼센트의 시간 동안 머리가 땅에 닿을 수 있는 동전에 고른 돈을 걸 것을 요청했다. 참가자들은 경기 시간이 30분이나 남았기 때문에 약 300개의 베팅을 할 수 있었고, 상금은 250달러로 제한되었다. 그러나 시험 대상자들의 행동은 최적과는 거리가 멀었다.

놀랍게도, 참가자들의 28%가 파산했고, 평균 봉급은 91달러에 불과했다. 참가자의 21%만이 최대치에 도달했다. 61명의 참가자 중 18명은 한 번의 토스에 모든 것을 걸었고, 3분의 2는 실험의 어느 단계에서 꼬리로 도박을 했다.^[9][10]

켈리 기준을 사용하고 실험의 확률에 기초하여(250달러 상한과 시험 기간 제한) 올바른 접근방식은 동전 던지기마다 자신의 자금줄의 20%를 베팅하는 것이 될 것이며, 이는 각 라운드당 평균 2.034%의 이득에 해당된다. 이것은 산술률 4%(1${\displaystyle +0.2}$ ${\displaystyle \cdot }$ 1${\displaystyle .0{}^{}}$) ${\displaystyle {0.6}^{}\cdot (1~0.2}$ ${\displaystyle \cdot 1}$.0${\displaystyle {}^{}}$) ${\displaystyle {0.4}^{}}$ ${\$.0$)^{0.6}\cdot (1-0.2\cdot$ 1.0$)^{0$.4$}}}$이 아니라 기하 평균이다$.$ 300라운드 이후의 이론적 기대 재산은 $10,505 ${\displaystyle 25}$ ${\displaystyle \cdot }$(${\displaystyle 1.02034{}^{}}$) ${\displaystyle {300}^{}}$ $(\$( $1.02034))$$^{300}}$ )은$($는) 뚜껑을 닫지 않은 경우.

특히 이번 경기에서는 상한선 때문에 각 토스에 12%의 솥만 베팅하는 전략이 훨씬 더 좋은 결과를 가져올 것이다(캡에 도달할 확률 95%와 평균 지불금 242.03달러).

도박식

내기에서 지는 것이 전체 내기를 잃는 것과 관련된 경우, 켈리의 내기는 다음과 같다.

${\displaystyle f^{*}=p-{\frac {q}{b}}=p+{\frac {p-1}{b}}}}$

여기서:

• $∗{\$은(는) 현재 뱅크롤에서 내기까지의 비율이다.
• $[\displaystyle p]$는 우승 확률이다.
• ${\displaystyle q}$ ${\displaystyle q}$은(${\displaystyle }$= 1${\displaystyle }$- ${\displaystyle p}$ ${\displaystyle q=1-p})$ 손실 확률이다.
• $[\displaystyle b]$는 승리와 함께 얻은 내기의 비율이다. 예: 2대 1의 확률로 10달러를 베팅할 경우(승산하면 30달러, 우승하면 20달러), $b{\displaystyle }$=${\displaystyle \mathrm{}\mathrm{20달러}}$/${\displaystyle \mathrm{}\mathrm{10달러}}$=$,$ 디스플레이 $스타일$ b$=\$20/\$10=2).$$0}$.
  

  그림에는 y축에 베팅할 포트폴리오의 분수에 대해 x축에서 승리한 금액이 표시된다. 이 수치는 p=0.5(승패 둘 다 확률이 50%인 것)를 가정한다. 우승으로 얻은 금액이 1이라면 켈리 베팅 금액은 0달러인데, 기대 이득이 없는 공정한 베팅에서는 말이 된다.

As an example, if a gamble has a 60% chance of winning (${\displaystyle p=0.6}$, ${\displaystyle q=0.4}$), and the gambler receives 1-to-1 odds on a winning bet (${\displaystyle b=1}$), then the gambler should bet 20% of the bankroll at each opportunity (${\displaystyle f^$${*}=0.6-{\frac {0.4}{1$}{1$}=0.2}$ ))$$의 장기적 성장률을 극대화하기 위해.

만약 도박꾼의 에지가 0이라면, 즉 $b{\displaystyle }$= ${\displaystyle q}$/ ${\displaystyle p}$ ${\displaystyle b=q/p}$이면, 그 기준은 도박꾼에게 아무것도 걸지 말라고 권고한다$.$

가장자리가 음수일 경우( </ p ${\displaystyle b<q/p$ 이 공식은 도박자가 내기의 다른 쪽을 택해야 함을 나타내는 부정적인 결과를 제공한다. 예를 들어 아메리칸 룰렛에서 벳터는 18개의 적색 번호와 20개의 비 적색 번호(${\displaystyle }$= ${\displaystyle 18}$/ ${\displaystyle 38}$ ${\displaystyle p=18/38})$가 있을 때, 적색 번호에 대해 균등한 금전 지급(b$$=${\displaystyle 1}$ ${\displaystyle b=1})$을 제공한다.$$ 켈리의 내기는 -${\displaystyle 1}$/ ${\displaystyle 19}$ $(\displaystyle -1/19)$이며$,$ 이는 도박꾼들이 빨간색이 올라오지 않을 것이라는 19분의 1의 돈을 걸어야 한다는 것을 의미한다. 룰렛에 비교할 수 있는 확률로 제공되는 명시적인 반 적색 베팅은 없기 때문에 켈리 도박사가 할 수 있는 최선의 방법은 아무것도 베팅하지 않는 것이다.

투자식

켈리 공식의 보다 일반적인 형태는 부분적인 손실을 허용하며, 이는 투자와 관련이 있다.

${\displaystyle f^{*}={\frac {p}{a}-{\frac {q}{b}}}.}$

여기서:

• $∗{\$는 보안에 적용할 자산의 일부분이다.
• ${\displaystyle p}$ $[\displaystyle p}$는 투자가치가 증가할 확률이다.
• ${\displaystyle q}$ ${\displaystyle q}$은(${\displaystyle }$= 1${\displaystyle }$- ${\displaystyle p}$ ${\displaystyle q=1-p})$ 투자가 감소할 확률이다$$.$$
• ${\displaystyle a}$ $[\displaystyle a}$은(는) 부정적인 결과에서 손실되는 분율이다. 예$)$ 보안 가격이 10% 하락하면 $a{\displaystyle }$= ${\displaystyle 0}$.1${\displaystyle a=0$.$1}$
• ${\displaystyle b}$ $(\displaystyle b)$는 긍정적인 결과로 얻어지는 부분이다. 예) 보안 가격이 10% 오르면 $b{\displaystyle }$= 0${\displaystyle b=0.$1$\}$

Kelly Criteria는 알려진 결과 확률에만 유효하며, 투자의 경우는 그렇지 않다. 켈리 부분 전체를 투자하는 것은 권장되지 않는다.

이 공식은 켈리의 분율이 1보다 높게 나타날 수 있다. 이 경우 레버리지(leverage)를 활용해 마진 상태에서 추가 증권을 매입하는 것이 이론적으로 유리하다.

증명

켈리 기준에 대한 경험적 발견은 간단하다.^[11] 켈리 기준은 부의 로그의 기대치를 최대화한다(함수의 기대값은 모든 가능한 결과에 대해 각각의 특정 결과의 확률에 그 결과의 경우 함수의 값을 곱한 합계에 의해 주어진다). 우리는 1단위의 부로 시작해서 $확률{\displaystyle }$ p ${\displaystyle p}$과(와) 함께 발생하며 $b{\displaystyle }$ ${\displaystyle b$}의 확률을 제공하는 결과에 그 부의 $일부$ f$${\$displaystyle f}$을(를) 걸었다$.$ 당첨 확률은 $p{\displaystyle }$ ${\displaystyle$ p$}$이고$,$ 그 경우 결과적으로 $부가{\displaystyle \mathrm{}}$ 1 +${\displaystyle f}$ ${\displaystyle b}$ ${\displaystyle 1+fb}$과 같다$.$ 손실 확률은 ${\displaystyle \mathrm{q}}$= 1${\displaystyle }$- ${\displaystyle p}$ ${\displaystyle q=1-p}$이며$,$ 이 경우 결과 부는 $1{\displaystyle \mathrm{}}$- ${\displaystyle f}$ ${\displaystyle a}$ ${\displaystyle 1-fa}$과 같다$.$ 따라서 예상되는 기하급수적 증가율 $r{\displaystyle }$ ${\displaystyle r}$은 다음과$$ 같다.

${\displaystyle r=(1+fb)^{p}\cdot(1-fa)^{q}}$

우리는 이 곡선의 최대 r을 찾고 싶다. 이 곡선은 방정식의 파생물을 찾는 것을 포함한다. 이것은 양쪽의 로그부터 먼저 가져가면 더욱 쉽게 완성된다. 결과 방정식은 다음과 같다.

${\displaystyle E=\log(r)=p\log(1+fb)+q\log(1-fa)}$

로그 부의 증가를 나타내는$$ $E{\displaystyle }$ ${\displaystyle E}$과(와) 함께. $f{\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$ ${\$로 표시된 $증가율$을 최대화하는$$ f ${\displaystyle f^}$의 값을 찾기 위해 위의 식을 구분하여 0으로 설정한다$.$ 이를 통해 얻을 수 있는 이점:

$왼쪽.{\frac {dE}{df}}\오른쪽 _{f=f^{*}}={{f=frac {pb}{1+f^{*b}}+{\frac {-qa}{1-f^{*}a}}}}}=0}$

$∗{\$의 값에 대해 해결하기 위해 이 방정식을 재배열하면 Kelly 기준이 된다$$.

${\displaystyle f^{*}={\frac {p}{a}-{\frac {q}{b}}}}}$

$이{\displaystyle }$ 표현식은 a${\displaystyle }$= ${\displaystyle 1}$= ${\displaystyle 100\mathrm{}}$%$${\$displaystyle a=1=$100$\backslash \%\}$이(가) 손실 때문에 내기가 완전히 손실되는 경우 단순한 도박 공식으로 줄어든다는 점에 유의하십시오.

베르누이

1738년 기사에서 다니엘 베르누이는 베팅이나 투자의 선택이 있을 때 가장 높은 기하학적 평균의 결과를 가진 것을 선택해야 한다고 제안했다. 이것은 비록 동기가 완전히 다르지만, 수학적으로 켈리 기준과 동등하다(베르누엘리는 성도를 해결하기를 원했다). 페테르부르크 역설).

베르누이 기사의 영문 번역본은 1954년에야 출판되었지만,^[12] 이 작품은 수학자와 경제학자들 사이에서 잘 알려져 있었다.

주식시장적용

수학 금융에서, 보안 가중치가 기대되는 기하학적 증가율(로그 부를 최대화하는 것과 동등한)을 최대화하면 포트폴리오를 성장 최적이라고 한다.^{[citation needed]}

성장 최적 포트폴리오의 계산은 엄청난 쓰레기와 쓰레기 배출 문제를 겪을 수 있다.^{[citation needed]} 예를 들어, 아래 사례들은 다양한 자산의 기대수익률과 공분산 구조를 감안한 것으로 간주하지만, 이러한 매개변수는 기껏 추정하거나 유의적인 불확실성으로 모형화한다. 성장 최적 포트폴리오의 사후 성능은 추정 오차에 의해 포트폴리오 가중치가 크게 좌우될 경우 이전 예측과 환상적으로 다를 수 있다. 매개변수 불확실성과 추정오차를 다루는 것은 포트폴리오 이론에서 큰 주제다.^{[citation needed]} 알려지지 않은 위험을 상쇄하기 위한 접근방식은 켈리 기준(예: 절반)보다 적게 투자하는 것이다.

비판

장기적으로 다른 어떤 전략보다 잘하겠다는 켈리 전략의 약속은 설득력이 있어 보이지만, 일부 경제학자들은 주로 개인의 특정 투자 제약이 최적의 성장률을 원하는 것보다 우선할 수 있기 때문에 그것에 대해 격렬하게 반대해 왔다.^[8] 전통적인 대안은 결과의 기대 효용성을 최대화할 수 있도록 베팅의 크기를 조정해야 한다는 기대 효용 이론이다(로그 효용성을 가진 개인에게, 켈리 베팅은 기대 효용성을 최대화하므로 갈등이 없다). 더욱이 켈리의 원문은 감블린의 경우 효용 함수의 필요성을 분명히 밝히고 있다.g게임은 여러번^[1] 하는 게임이다. 켈리 지지자들조차 대개 소수 켈리(켈리가 추천한 금액의 고정 부분을 더하는 것)를 주장하는데, 이는 변동성을 줄이기를 바라거나, 유리(에지) 계산에서 비결정적 오류로부터 보호하려는 등 다양한 현실적인 이유 때문이다.^[13]

고등수학

엄격하고 일반적인 증거는 켈리의 원본 논문이나^[1] 아래에 나열된 다른 참고 문헌을 참조하십시오. 일부 수정 사항이 발표되었다.^[14] $우리$는 b =${\displaystyle 1}$ ${\displaystyle b=1}$ $$(50:50 "짝수" 내기)를 가진 사건에 대해 다음과 같은 비강제적인 주장을 하여 일반적인 생각을 보여주고 약간의 통찰력을 제공한다.^[1] $b{\displaystyle }$= ${\displaystyle 1}$ ${\displaystyle b=1}$일$$때 켈리 베터는 위와 같이 초기 재산 $W{\displaystyle }$ ${\displaystyle W}$의 ${\displaystyle \mathrm{2p}}$ ${\displaystyle -}$ ${\displaystyle 1}$을$$베팅한다$.$ 만약 그들이 이기면, 그들은 한 번의 내기를 거쳐$$ ${\displaystyle \mathrm{2p}}$ W$[\displaystyle 2pW]$를 갖게 된다. 만약 그들이 지면, $그들$은 2${\displaystyle }$( ${\displaystyle 1}$-${\displaystyle p}$ ) ${\displaystyle W}$ ${\displaystyle 2(1-p)W}$을 갖게 된다$.$ 그들이 $이렇게{\displaystyle }$ N$${\$displaystyle N}$을 $베팅$하고, $이{\displaystyle }$일련의 N {\$displaysty N}$ 베팅$$ 중에서 K$${\$displaysty K}$을 이긴다고 가정해보자. 이에 따른 부는 다음과 같다.

${\displaystyle 2^{N}p^{K}(1-p)^{{N-K}W\!}$

승패의 순서는 결과의 부에 영향을 미치지 않는다는 점에 유의한다. 다른 베터가$\Delta {\displaystyle \mathrm{}}$ {\$displaystyle$ \Delta $$$}$의 일부 값에 대해 ${\displaystyle W}$ ${\displaystyle (2p-1+\Delta )W}$의 다른 금액을 베팅한다고 가정합시다(여기서 $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle \Delta }$은 양수 또는 음수). 우승 후$$${\displaystyle }$(${\displaystyle \mathrm{2p}}$ +${\displaystyle \mathrm{\Delta }}$) ${\displaystyle W}$ ${\displaystyle$(${\displaystyle \mathrm{2p}}$$+\Delta )W},$ 패배 후에는${\displaystyle }$[ 2${\displaystyle }$( ${\displaystyle 1}$ -${\displaystyle p}$)${\displaystyle }$- ${\displaystyle \mathrm{\Delta }}$ ${\displaystyle ]}$ ${\displaystyle W}$ ${\displaystyle [2(1-p)-\Delta ]W}$을 갖는다. 켈리 베토르와 같은 일련의 승패 후에, 그들은 다음과 같은 결과를 얻게 될 것이다.

${\displaystyle(2p+\Delta )^{K}[2(1-p)-\Delta ]^{{N-K}W}$

$\Delta {\displaystyle \mathrm{}}$ ${\displaystyle \Delta }$과(와) 관련된 파생 모델을 살펴보고$$ 다음을 확인하십시오.

${\displaystyle K(2p+\Delta )^{K-1}[2-p)-\Delta ]^{{N-K}W-(N-K)-(2p+\Delta )^{K}[2(1-p)-\Delta ]^{N-K-1}W}W}$

이 파생상품이 0과 같을 때 함수는 최대화된다.

$(\displaystyle K[2-p)-\Delta ]=(N-K)(2p+\Delta )}$

라는 것을 암시한다.

${\displaystyle \Delta =2\왼쪽({\frac {K}{N}-p\오른쪽)}$

그러나 내기에서 이긴 비율은 결국 다음과 같이 수렴될 것이다.

${\displaystyle \lim _{N\to +\inflat }{\frac {K}{N}=p}$

대수의 약한 법칙에 따라 그래서 장기적으로는 $\Delta {\displaystyle \mathrm{}}$ ${\displaystyle \Delta}$을(를) 0으로$$ 설정함으로써 최종 부를 극대화하게 되는데, 이는 켈리 전략을 따른다는 뜻이다. 이것은 켈리가 결정론적 요소와 확률론적 요소를 모두 가지고 있음을 보여준다. K와 N을 알고 매번 베팅할 부의 일정한 부분을 선택하고자 한다면(그렇지 않으면 부정행위를 할 수 있고, 예를 들어 나머지 베팅이 지는 것을 알고^th K가 이긴 후에 0을 걸 수 있다) 다음과 같이 베팅하면 가장 많은 돈이 된다.

${\displaystyle \left(2{\frac {K}{N}-1\right)W}$

매번 $N{\displaystyle }$ ${\displaystyle N}$이(가) 작든 크든 마찬가지다. 때문에 K사전에 알려져 있지 않다로 N{N\displaystyle} 크면 방금 K{K\displaystyle}N{pN\displaystyle}이 항목에 접근할 것이다 켈리"장기적"부분입니다. K입니다. 켈리 이상 bets 누군가 더 잘 할 수 있고, 앉은 자리에 안 내려 N{\displaystyle K>, pN}, 켈리 이하 bets 누군가 d.이 필요합니다베트 OOO< ${\displaystyle K<pN}$을(를) 스트레칭으로 보나, 장기적으로는 켈리가 항상 승리한다. 일반 사건에 대한 경험적 발견은 다음과 같이 진행된다.^{[citation needed]} 단 한 번의 시험에서 자본의$$ $분수{\displaystyle }$ f ${\displaystyle f}$을(를) 투자하고, 전략이 성공하면 재판 말기의 자본이 $인자{\displaystyle \mathrm{}1}$ -${\displaystyle }$f + ${\displaystyle f}$(${\displaystyle }$1${\displaystyle }$+ ${\displaystyle b}$) = ${\displaystyle 1}$+ f ${\displaystyle 1-f+f (1+b)=1+fb}$만큼 증가하며$,$ 마찬가지로 전략이 실패하면 결국 자본이 인자 $1$만큼 감소하게 된다.$-$ ${\displaystyle f}$ ${\displaystyle 1-fa}$ 따라서 $N{\displaystyle }$ ${\displaystyle N}$ 재판$$(${\displaystyle p}$ N ${\displaystyle pN}$ 성공$$ 및 Q ${\displaystyle N}$ ${\displaystyle qN}$ 실패$$) 종료 시 1달러의 초기 자본이 산출된다.

${\displaystyle C_{N}=(1+fb)^{pN}(1-fa)^{qN}}$

${\displaystyle 로그}$log${\displaystyle }$(${\displaystyle C_{}}$N )${\displaystyle }$/ N$${\$displaystyle \log(C_{N}/N$를 최대화하면 $결과적$으로 C ${\displaystyle N_{}}$ ${\$$displaystyle C_$${N}$이$($가$)$ 원하는 결과를 얻을$$ 수 있음

${\displaystyle f^{*}=p/a-q/b.}$

에드워드 O. Thorp은 일반적인 경우를 위해 이 공식에 대해 더 자세한 논의를 제공했다.^[15] $거기$에서 $p{\displaystyle }$ ${\displaystyle p}$을(를) 시험 횟수에 대한 "성공자 수"의 비율에 대해$$ 대체하는 것은 시험 횟수가 무한대로 가면서 이 비율의 한계로 정의되기$$ 때문에 시험 횟수가 매우 많아야 함을 시사한다고 볼 수 있다. 요컨대 매회 $∗{\$ f$^{*}}}$을 베팅하면 재판 횟수가 매우 많은 경우에만 재산증가율을 극대화할 가능성이 높고, $p{\displaystyle }$ ${\displaystyp$ p$}$와 b ${\displaystyb}$은 $재판$마다 동일하다$$. 실제로 이것은 같은 게임을 반복해서 하는 문제인데, 승산과 승산이 항상 같다. 위의 경험적 발견에서 ${\displaystyle p}$ N ${\displaystyle pN}$ 성공과$$ Q ${\displaystyle N}$ ${\displaystyle qN}$ 실패는$$ 매우 큰 $N{\displaystyle }$ ${\displaystyle$ N$\}$에 대해서만 발생할 가능성이 높다.

다중 결과

켈리의 기준은 경마와 같이 상호 배타적인 많은 결과에 대한 도박에서 일반화될^[16] 수 있다. 서로 배타적인 결과가 몇 가지 있다고 가정하자. $k{\displaystyle }$ ${\displaystyle k}$ -th$$ 말이 경주에서 이길 확률은 ${\displaystyle p_{}}$ $k{\displaystyle {}_{}}$ ${\$이고$,$ $k{\displaystyle }$ ${\displaystyle k}$ -th$$ 말에 걸린 내기의 총량은 ${\displaystyle B_{}}$ k ${\$이고, 그리고$,$

${\displaystyle \beta _{k}={\frac {B_{k}}{\sum_{i}B_{i}}}={\frac {D}{1+Q_{k}}}}}}}}}}}$

$여기$서 Q ${\displaystyle k_{}}$ ${\$는 보상의 확률이다$$. ${\displaystyle D}$= ${\displaystyle 1}$- ${\displaystyle t}$ ${\displaystyle D$$=1-tt}$은$$${\displaystyle t}$ ${\displaystyle tt}$이(가) 트랙 테이크 또는 세금인$$ 배당률이고, $D{\displaystyle }$ ${\displaystyle \frac{{}_{}}{}}$ ${\displaystyle \frac{k_{}}{}}$ ${\displaystyle$ {$D}{\frac{\$frac}{\$beta _{k$$}}}}}}}}}$는 트랙 테이크 공제 후의 수익률이다$$. $k{\displaystyle }$ ${\displaystyle k}$ -th$$ hors에 베팅할 벳토어의 자금의 ${\displaystyle {분수}_{}}$는 f$$k {\$displaystyle$f_${k$ 켈리의 상호 배타적인 여러 결과를 가진 도박에 대한 기준은 최적의 S ${\displaystyle o^{}}$ ${\$를 찾아 내기 위한 알고리즘을 제공하며, 그 결과들은$$ 합리적이고 명시적이다. 최적 세트 $S{\displaystyle {}^{}}$ ${\displaystyle o^{}}$ ${\$에 포함된 결과에 베팅할 벳토르 재산의$$ 최적 $분수{\displaystyle {}_{}^{}}$ f ${\displaystyle k_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$ S$^{o$ 최적의 결과 집합을 위한 알고리즘은 4단계로 구성된다.^[16]

1단계: 가능한 모든 결과(또는 가장 유망한 몇 가지 결과에 대해서만)에 대한 예상 수익률을 계산하십시오.

${\displaystyle er_{i}={\frac {Dp_{i}}{\beta_{i}}=p_{i}(Q_{i}+1)}}$

2단계: 새로운 시퀀스 $e{\displaystyle }$ r ${\displaystyle k_{}}$ ${\$이(가) 증가하지 않도록$$ 결과를 다시 정렬하십시오. 따라서 $e{\displaystyle }$ ${\displaystyle {}_{}}$ ${\$}가 가장 좋은 방법이 될 것이다$$.

3단계: $Set{\displaystyle }$ S${\displaystyle }$= ${\displaystyle \varnothing }$ ${\displaystyle S=\varnot }($빈 세트), ${\displaystyle \mathrm{k}}$= $1{\displaystyle }$ ${\displaystyle k=1$ $R{\displaystyle (S}$ ${\displaystyle )}$= 1 ${\displaystyle R(S)=1.$ 따라서 최상의 e r ${\displaystyle {}_{}}$ = e${\displaystyle {}_{}{r}_{}}$ ${\displaystyle {}_{}}$ {\$displaystystystyle er_{$1}을 먼저 고려한다$.$

4단계: 반복:

If ${\displaystyle er_{k}={\frac {D}{\beta _{k}}}p_{k}>R(S)}$ then insert ${\displaystyle k}$-th outcome into the set: ${\displaystyle S=S\cup \{k\}}$, recalculate ${\displaystyle R(S)}$ according to the formula:

${\displaystyle R(S)={\frac {D\sum _{k\notin S}p_{k}}{D-\sum _{k\in S}\beta _{k}}}}$ and then set ${\displaystyle k=k+1}$,

그렇지 않으면 $S{\displaystyle {}^{}}$ ${\displaystyle o^{}}$= ${\displaystyle S}$ ${\displaystyle S^{o}=S}$를 설정하고$$ 반복을 중지하십시오.

최적 세트 $S{\displaystyle {}^{}}$ ${\displaystyle o^{}}$ ${\$가 비어$$ 있는 경우, 전혀 베팅하지 마십시오. 최적 결과의$$ $S{\displaystyle {}^{}}$ ${\displaystyle o^{}}$ ${\$이(가) 비어 있지 않으면 k ${\displaystyle f_$${k}^{o}}$에 베팅할$$ 최적 분율$$ fk ${\displaystyle o_{}^{}}$}은(는) $다음{\displaystyle }$ 공식에서 계산할 수 있다.

${\displaystyle f_{i}=p_{i}-\beta _{i}{\frac {\sum _{k\notin S}p_{k}}{(D-\sum _{k\in S}\beta _{k})}}}$.

라는 것을 증명할^[16] 수도 있다.

${\displaystyle R(S^{o}=1-\sum _{i\in S^{o}}{f_{i}^{o}}}}}}$

여기서 오른쪽은 예비율이다^{[clarification needed]}. 만일이 예상 수익률은 그러므로, 요건 erk=Dβ kpk>R({\displaystyle er_{k}={\frac{D}{\beta_{k}}}p_{k}>, R(S)}다음과 같이:k{k\displaystyle}-th 결과 최적의 결과의 집합 S시{\displaystyle S^{는 o}}에 포함된다 interpreted[16] 수 있정확'r'의 han이자율을 유지하다 최적분수 $f{\displaystyle {}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$에 대한 $공식$은 k ${\displaystyle$ k$}$ -th$$ 말이 우승할 때 트랙 테이크 차감 후 수익으로 나눈 예비율을 $k{\displaystyle }$ ${\displaystyle$ $k$$}$ -th$$ 말의 예상수익률을 초과하거나, 또는 확률 초과한 것으로 해석할 수 있다$$. ${\displaystyle }$$k{\displaystyle }$ ${\$$displaystyle k}$ -th$$ 말은 k {\$displaysty k}$ -th$$ 말이 우승할 때 트랙 테이크 차감 후 예비율을 수익으로 나눈 승마에 이긴다. 이항 성장 지수:

${\displaystyle G^{o}=\sum_{p_{i}\log_{2}{{2}+(1-\sum_{p_{i}})\log _{2}{{2}(R(S^{o})}}}}}}}}$

그리고 두 배의 시간은

${\dplaystyle T_{d}={\frac {1}{G^{o}}}.}$

이 최적의 베팅 선택 방법은 ${\displaystyle {확률}_{}}$ p ${\$이 가장 유망한 몇 가지 결과에 대해서만 알려져 있는$$ 반면 나머지 결과는 승산이 없는 경우에도 적용할 수 있다. 이 경우 는 틀림없었다.

< ,${\displaystyle \sum _{i}{p_{i}}}$ 및

< ${\displaystyle \sum _{i}{\reason _{i1$

주식투자

2차 테일러 다항식(Taylor polyomial)은 주요 기준의 좋은 근사치로 사용할 수 있다. 주로 기존 과거 자료에서 쉽게 추정할 수 있는 단순한 특징(기대가치와 변동)에 기초하여 투자에 할애하는 비율이 주식투자에 유용하다. 이 근사치는 견고하고 원래 기준과 유사한 결과를 제공하는 결과를 초래한다.^[17]

단일자산(주식, 인덱스펀드 등), 무위험이자율의 경우 기하학적 브라운 모션을 통해 투자하기에 최적의 분율을 얻기 쉽다. 시간 $t{\displaystyle }$ ${\displaystyle t}($${\displaystyle {}_{}}$ ${\displaystyle t_{}}$ ${\$에서 로그 정규 분포 자산 $S{\displaystyle }$ ${\displaystyle S}$의 값은 다음과 같다.

${\displaystyle S_{t}=S_{0}\exp \left(\mu -{\frac {\sigma ^{2}}:\오른쪽)+\시그마 W_{t}\rigma W_{t}$

$W{\displaystyle {}_{}}$ ${\displaystyle t_{}}$ ${\$가 Wiener 공정이고 μ ${\displaystyle \mu }($백분율 드리프트)와 $\mu {\displaystyle }$ ${\displaystyle \sigma }($백분율 변동성)가 상수인 기하학적 브라운 운동 솔루션으로부터. 로그 기대치:

${\displaystyle \mathb{E} \log(S_{0})=\log(S_{0})+\left(\mu -{\frac {\sigma ^{2}}:\오른쪽)t.}$

그러면 기대 로그 리턴 ${\displaystyle R_{}}$ s ${\$이(가)

${\displaystyle R_{s}=\left(\mu -{\frac {\sigma ^{2}}:}\오른쪽)s.}$

$자산{\displaystyle }$$$ $S{\displaystyle }$ ${\displaystyle S}$과$($와) 결합의 S ${\displaystyle S}$ 및$$${\displaystyle }$($1$- $)$에 $부분{\displaystyle }$ f ${\$$displaystyle$ $f}$이(가$)$ 투자된 채권의 경우 예상되는 1주기 $수익률$이 다음과 같다.

${\displaystyle \mathbb {E} \left(f\left[{\frac {S_{1}}{S_{0}}}-1\right]+(1-f)r\right)=\mathbb {E} \left(f\left[\exp \left(\left(\mu -{\frac {\sigma ^{2}}{2}}\right)+\sigma W_{1}\right)-1\right]\right)+(1-f)r}$

그러나 사람들은 Kelly의 맥락에서 1주기 동안$$ 예상되는 로그 반환 $G{\displaystyle }$(${\displaystyle f}$) {\$displaystyle$ G$(f)}$을(를) 처리하는 것처럼 보인다.

${\displaystyle G(f)=f\mu -{\frac {(f\sigma )^{2}}+(1-f)\r).}$

${\displaystyle 최대값(G}$( ${\displaystyle f}$)${\displaystyle \max(G(f)})}$ 해결$$

${\displaystyle f^{*}={\frac {\mu -r}{\ma ^{2}}.}$

$∗{\$는 기대 로그 반환을 최대화하는 분수로서, 켈리 분율도 그렇다. 토프는^[15] 같은 결과를 얻었지만 다른 파생을 통해 도달했다. ${\displaystyle \mu}$이(가) 자산 로그 반환 ${\displaystyle R_{}}$ s ${\$와 다르다는$$ 것을 기억하라$.$ 혼란스러운 것은 켈리 기준에 대해 이야기하는 웹사이트와 기사에서 흔히 저지르는 실수다.

복수의 자산에 $대해서$는 확률적 ${\displaystyle {수익률}_{}}$ r k$$${\$$displaystyle r_{k$${\displaystyle \mathrm{k}}$ = $1{\displaystyle }$,${\displaystyle }$.${\displaystyle n}$, {\$displaystyle$ k$=1$, $...,n},$ 리스크$$ 없는 채권과 r{\$displaystyle r}$이 있는 $시장$을 고려한다$.$ 투자자는 practice ${\displaystyle u_{}}$ k ${\displaystyle {}_{}}$을(를)에 넣는다.$\displaystyle u_{k}}$ 자본의$$ \displaystyle $S_${k}}}을$$(를) $S{\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$ S_${k}}}}$에 표시하고 나머지는 채권에 투자 일반성을 상실하지 않는 한, 투자자의 출발 자본이 1과 같다고 가정한다. Kelly 기준에 따라 최대화해야 한다.

${\displaystyle \mathb {E} \left[\ln \left(1+r)]+\sum \limits _{k=1}^{nu_{k}(r_{k}-r)\right].}$

Taylor 시리즈로 확장하여 ${\displaystyle \stackrel{}{{u\mathrm{}}_{}}}$ 0${\displaystyle \stackrel{}{{}_{}}}$→${\displaystyle }$=${\displaystyle }$( ${\displaystyle 0}$,${\displaystyle }$…${\displaystyle }$, ${\displaystyle 0}$) ${\displaystyle {\vec {u_{0}}=(0,\ldots ,0)}$을(를) 얻음

${\displaystyle \mathbb {E} \left[\ln(1+r)+\sum \limits _{k=1}^{n}{\frac {u_{k}(r_{k}-r)}{1+r}}-{\frac {1}{2}}\sum \limits _{k=1}^{n}\sum \limits _{j=1}^{n}u_{k}u_{j}{\frac {(r_{k}-r)(r_{j}-r)}{(1+r)^{2}}}\오른쪽].}$

따라서 최적화 문제를 2차 프로그래밍으로 줄이고 제약 없는 솔루션은

${\displaystyle {\vec{u^{\star }}=(1+r)({\widehat {\Sigma }}})^{-1}({\widehat {\vec}-r)}$

$여기$서 r${\displaystyle \stackrel{}{\stackrel{}{}}}$→ $^{\$ 및$$ $^{\$은(는) 수단의 벡터 및 초과 반환의 두 번째 혼합된 비중앙 모멘트의 행렬이다$$. 또한 부분 켈리 전략과 레버리지와 공매도 제약이 없는 최적의 솔루션을 위한 수치 알고리즘이 있다.^[18]

참고 항목

• 파멸위험
• 도박정보이론
• 프롭스팅의 역설
• 머튼의 포트폴리오 문제

참조

외부 링크

위키북스는 켈리_크리테리아라는 주제에 관한 책을 가지고 있다.