학습곡선

학습 곡선은 사람들이 과제에 얼마나 능숙한지와 그들이 가진 경험의 양 사이의 관계를 그래픽으로 표현한 것입니다.숙련도(수직축으로 측정)는 보통 경험이 증가할수록(수직축으로 측정) 증가합니다. 즉, 누군가, 그룹, 회사 또는 산업체가 어떤 일을 더 많이 수행할수록 그 ^[1]일을 더 잘 수행할 수 있습니다.

일반적인 표현인 "급격한 학습 곡선"은 활동이 배우기 어렵고 많은 노력을 들여서 숙련도가 크게 향상되지 않는다는 잘못된 이름입니다. 비록 시작이 가파른 학습 곡선은 실제로 빠른 ^[2][3]발전을 나타냅니다.사실 곡선의 기울기는 활동의 전체적인 난이도와는 무관하지만 시간에 따른 학습 속도의 예상 변화율을 나타냅니다.기본적인 것은 익히기 쉽지만 숙달하기 어려운 활동은 "가파적인 학습 곡선"^{[citation needed]}을 가진 것으로 묘사될 수 있습니다.

학습 곡선은 특정 과제 또는 지식체를 지칭할 수 있습니다.헤르만 에빙하우스(Hermann Ebinghaus)는 1885년 학습 심리학 분야에서 학습 곡선을 처음으로 설명했습니다.^[4][5]1936년에 Theodore Paul Wright는 항공기 ^[6]산업의 생산 비용에 대한 학습의 효과를 묘사했습니다.단위 비용을 총 생산에 대해 표시하는 이 형태를 경험 곡선이라고 부르기도 합니다.

심리학에서

Hermann Ebinghaus의 시험은 일련의 말도 안 되는 음절들을 암기하고, 많은 시험들에서 성공을 기록하는 것을 포함했습니다.번역본에서는 '학습 곡선'이라는 용어를 사용하지 않지만, 시험 번호에 대한 학습 다이어그램을 제시합니다.그는 또한 점수가 줄어들거나 심지어 ^[4][3][7]진동할 수도 있다고 언급합니다.

'학습 곡선'이라는 용어의 첫 번째 사용으로 알려진 것은 1903년의 것입니다: "브라이언과 하터(6)는 전신 언어의 습득에 대한 그들의 연구에서 학습 곡선이 초기에 급격하게 증가하고 학습 속도가 느려져서 수직 ^[5][3]축으로 볼록한 것을 발견했습니다."

심리학자 아서 빌스는 1934년에 학습곡선에 대해 더 자세하게 설명했습니다.그는 또한 음가속도, 양가속도, 고원 및 오가브 ^[8]곡선과 같은 다양한 유형의 학습 곡선의 특성에 대해 논의했습니다.

경제학에서

역사

1936년, Theodore Paul Wright는 항공기 산업의 생산 비용에 대한 학습의 효과를 설명하고 학습 ^[6]곡선의 수학적 모델을 제안했습니다.

1952년 미 공군은 1940년부터 1945년 ^[9]중반까지 기체 산업의 학습 곡선에 대한 데이터를 발표했습니다.구체적으로, 그들은 다양한 제품의 직접적인 인건비를 누적 생산 함수로 표화하여 표시했습니다.이것은 1950년대에 ^[10]학습 곡선에 대한 많은 연구의 기초를 형성했습니다.

1968년 보스턴 컨설팅 그룹(BCG)의 브루스 헨더슨(Bruce Henderson)은 Wright에 의해 개척된 단위 비용 모델을 일반화했으며, 구체적으로 "헨더슨의 ^[11]법칙"이라고도 불리는 Power Law를 사용했습니다.그는 이 특별한 버전을 ^[12][13]경험 곡선이라고 이름 지었습니다.1970년대 BCG의 연구는 10%^[14]에서 25%에 이르는 다양한 산업에 대한 경험 곡선 효과를 관찰했습니다.

모델들

학습 곡선의 주요 통계 모형은 ^[15][16]다음과 같습니다.

• Wright의 모형("로그-선형"): $y$ = ${\displaystyle {}^{}}$ x ${\displaystyle n^{}}${\$displaystyle$ y = $Kx^{n$ 여기서
  • ${\displaystyle }$y$${\$displaystyle$ y$}$은$($는) x {\$displaystyle$ x$}$ 단위의 비용입니다.
  • ${\displaystyle x}$ ${\displaystyle$ x$}$은(는) 만들어진 총 단위 수입니다.
  • ${\displaystyle K}$ ${\displaystyle$ K$}$은(는) 처음 만들어진 단위의 비용입니다.
  • ${\displaystyle n}${\$displaystyle$ n$}$은 학습의 강도를 측정하는 지수입니다.
• 플래토 모델: $y$ =${\displaystyle max}$ (${\displaystyle {}^{}}$ ${\displaystyle x^{}}$ n${\displaystyle {}^{}}$ ${\displaystyle 0_{}}$ )$${\$displaystyle$ y =\$max (Kx^{n}, K_{0$ $여기$서 K ${\displaystyle 0_{}}${\$displaystyle$ K_${0}}$은(는) 달성 가능한 최소 비용을 모델링합니다.즉, 비용이 충분히 낮은 수준에 도달한 후 학습이 중단됩니다.
• Stanford-B 모델: $y$ =${\displaystyle K}$ (${\displaystyle x}$ +${\displaystyle {}^{}B}$ ) ${\displaystyle n^{}}${\$displaystyle$ y =$K$ ($x$+ $B)^{n$ $여기$서 B$${\$displaystyle$ B$}$는 작업자의 사전 경험을 모델링합니다.
• DeJong의 모델: $y$ =${\displaystyle K}$ (${\displaystyle M}$+ ( 1${\displaystyle }$-${\displaystyle }$M ) ${\displaystyle x^{}}$n )$${\$displaystyle$ y =$K$ ( $M$+ ( $1$ -$$ ) $x^{n}$ $)\},$ $여기$서 M ${\displaystyle$ M$}$은(인간 작업자와 달리 학습할 수 없는) 기계가 수행하는 생산 분율을 모델링합니다.
• S-곡선 모형 : $y$ =${\displaystyle K}$ ( M${\displaystyle }$+ ( ${\displaystyle 1}$-${\displaystyle }$M${\displaystyle }$) (${\displaystyle x}$ +${\displaystyle {}^{}B}$ )${\displaystyle n^{}}$ )$${\$displaystyle$ y =$K$ ( $M$+ ( 1 - ${\displaystyle M}$) ($x$ + B$)^{n$ Stanford-B 모형과 DeJong 모형의 조합.

핵심 변수는 학습의 강도를 측정하는 $지수{\displaystyle }$ n$${\$displaystyle$ n$}$입니다.일반적으로 n = ${\displaystyle \log }$ ⁡ ( ${\displaystyle 2}$) / ${\displaystyle \log }$ ⁡ (${\displaystyle }$ϕ )$${\$displaystyle$ n =\$log(2)/\$log(\$phi$ $)\}$로 표시되며, 여기서 ϕ ${\displaystyle \phi }$는 "학습 속도"입니다.즉, 전체 단위를 두 배로 늘릴 때마다 단위 비용이 1${\displaystyle }$-$$ϕ ${\displaystyle 1-$\phi$\}만큼$ 감소한다는 것을 의미합니다.Wright은 항공기 제조에서 ${\displaystyle \mathrm{\Delta 80}}${\$displaystyle \phi \approx$ 80$\%}$이 발견되었으며, 이는 제조된 총 단위를 두 배로 늘릴 때마다 단위 비용이 20% 감소한다는 것을 의미합니다.

적용들

생산성과 효율성에 대한 경제적 학습은 일반적으로 같은 종류의 경험 곡선을 따르며 흥미로운 2차 효과를 갖습니다.효율성 및 생산성 향상은 개인뿐만 아니라 전체 조직 또는 산업 또는 경제 학습 프로세스로 간주될 수 있습니다.일반적인 패턴은 실제로 달성 가능한 방법론 개선 수준에 도달함에 따라 먼저 속도를 높이다가 속도를 낮추는 것입니다.개선된 방법을 학습함으로써 지역의 노력과 자원 사용을 줄이는 효과는 1880년대 Jevons 역설에서 논의되고 1980년대 Kazoom-Brookes Postulate에서 업데이트된 것처럼 확장 또는 경제 성장을 촉진함으로써 다음 대규모 시스템에 반대되는 잠재적 효과를 종종 가져옵니다.

경영 경제학에 대한 학습 곡선의 적용을 종합적으로 이해하면 전략적 차원에서 많은 이점을 얻을 수 있습니다.사람들은 신제품의 적절한 출시 시기를 예측하고 경쟁력 있는 가격 결정을 제공하며 제품에 대한 혁신을 촉진하고 조직 설계 ^[17]구조를 선택함으로써 투자 수준을 결정할 수 있었습니다.발라찬더와 스리니바산은 내구성이 뛰어난 제품과 그 가격 전략을 학습 곡선의 원리에 따라 연구하곤 했습니다.제품을 생산하고 판매하는 경험의 증가가 단가 하락을 초래할 것이라는 개념을 바탕으로 ^[18]이 제품에 대한 잠재적인 최고의 도입 가격을 찾았습니다.부족한 자원의 한계 하에서 생산 관리의 문제점에 관하여, 리아오는 노동 시간과 기계 시간에 대한 학습 곡선의 영향을 포함하지 않으면 사람들이 잘못된 경영 결정을 내릴 수 있다고 관찰했습니다.Demester와 Qi는 학습 곡선을 사용하여 구제품의 제거와 신제품의 도입 사이의 전환을 연구했습니다.그들의 결과는 최적의 전환 시간이 제품과 공정의 특성, 시장 요인, 그리고 이 제품에 대한 학습 곡선의 특징에 의해 결정된다는 것을 보여주었습니다.콘스탄타라스, 스쿠리, 자베르는 수요 예측 학습 곡선과 경제 질서 수량을 적용했습니다.그들은 구매자들이 학습 곡선을 따른다는 것을 발견했고, 이 결과는 재고 관리에 대한 의사 결정에 유용합니다.

학습 곡선은 반도체 ^[22]산업에서 무어의 법칙을 모델링하는 데 사용되었습니다.

임금이 생산 제품의 수에 비례할 때, 근로자들은 일시적으로 생산성을 떨어뜨릴 수 있기 때문에 다른 직책으로 바꾸거나 팀에 새로운 구성원을 두는 것을 거부할 수 있습니다.학습 곡선은 근로자들이 학습하는 ^[15]동안 동일한 제품에 대해 더 많은 보수를 받을 수 있도록 일시적인 하락에 대해 조정하는 데 사용되었습니다.

예제 및 수학적 모델링

학습 곡선은 경험이 있는 내재된 학습(숙련도 또는 한계에 대한 진행도)에 대한 대리 측정도입니다.

• 가로축은 경험을 직접 시간(시계 시간 또는 활동에 소요된 시간)으로 나타내거나, 시간(시행 횟수 또는 제작된 총 단위 수)과 관련될 수 있습니다.
• 세로축은 '학습', '숙련' 또는 '효율성' 또는 '생산성'에 대한 다른 대용치를 나타내는 척도입니다.테스트 점수가 증가하거나(예: 테스트 점수), 감소할 수 있습니다(테스트 완료 시간).

일련의 시도에서 한 사람이 수행할 경우 숙련도가 증가하거나 감소하거나 평탄화되는 등 곡선이 불규칙할 수 있습니다.

많은 수의 개별 시행의 결과가 평균화되면 부드러운 곡선이 생성되며, 이 곡선은 종종 수학적 함수로 설명될 수 있습니다.

• 

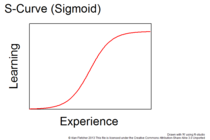
  S곡선 또는 시그모이드 함수

• 

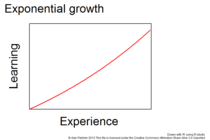
  기하급수적 성장

• 

  지수 상승 또는 하강을 한계로 합니다.

• 

  멱법칙

몇 가지 주요 기능이 ^[23][24][25]사용되고 있습니다.

• S-Curve 또는 Sigmoid 함수는 모든 학습 곡선의 이상적인 일반적인 형태이며, 학습 활동이 한계에 도달함에 따라 처음에는 천천히 작은 단계를 축적하고 나중에는 더 큰 단계를 거쳐 연속적으로 작은 단계를 생성합니다.그것은 배울 것의 발견에서 그것에 대한 학습의 한계까지 이어지는 정상적인 진행을 이상화합니다.다른 모양의 학습 곡선(4, 5 및 6)은 전체 범위 없이 S-곡선의 세그먼트를 보여줍니다.이 경우 숙련도의 향상은 천천히 시작한 다음 빠르게 증가하고 마지막으로 레벨을 바꿉니다.
• 지수 성장(exponential growth). 지수 성장(exponential growth)과 같이 숙련도를 제한 없이 높일 수 있습니다.
• 지수 상승 또는 하강이 한계에 도달합니다. 숙련도는 캐패시터가 저항기를 통해 충전 또는 방전(지수 붕괴)하는 방식과 유사한 방식으로 지수적으로 한계에 접근할 수 있습니다.기술의 증가 또는 정보의 보존은 초기 시도 동안 최대 속도로 빠르게 증가하고, 그 후 점차 레벨이 낮아져 나중에 반복할 때마다 피험자의 기술은 크게 향상되지 않고, 시간이 지남에 따라 습득되는 새로운 지식은 더 적어집니다.
• 거듭제곱 법칙; 지수 붕괴 함수와 외관이 유사하며, 비용과 같은 성능 저하 측정에 거의 항상 사용됩니다.또한 경험의 로그에 대한 숙련도 로그로 표시되면 결과가 직선이 되며 종종 이러한 방식으로 표시됩니다.

멱함수 법칙이 있는 단위 비용 대 총 생산량의 그림의 구체적인 경우를 경험 곡선이라고 이름 붙였습니다. 수학 함수는 때때로 헨더슨의 법칙이라고 불립니다.이러한 형태의 학습 곡선은 업계에서 ^[26]비용 예측을 위해 광범위하게 사용됩니다.

기계학습에서

성능과 경험을 연관시키는 플롯은 기계 학습에서 널리 사용됩니다.성능은 학습 시스템의 오류율 또는 정확도이며, 경험은 학습에 사용되는 훈련 예제의 수 또는 시스템 모델 ^[27]파라미터 최적화에 사용되는 반복 횟수일 수 있습니다.기계 학습 곡선은 여러 ^[28]알고리즘을 비교하고,^[29] 설계 중 모델 파라미터를 선택하고, 최적화를 조정하여 수렴을 개선하고,^[30] 교육에 사용되는 데이터의 양을 결정하는 등 여러 가지 목적에 유용합니다.

좀더 넓은 해석

처음에 교육 및 행동심리학에서 도입된 이 용어는 시간이 지남에 따라 보다 넓은 해석을 얻게 되었으며, '경험곡선', '개선곡선', '비용개선곡선', '진행곡선', '진행함수', '시동곡선', '효율곡선' 등의 표현이 혼용되는 경우가 많습니다.경제학에서 주제는 "개발"의 비율입니다. 개발은 다양한 진행률을 가진 전체 시스템 학습 과정을 의미하기 때문입니다.일반적으로 모든 학습은 시간이 지남에 따라 점진적인 변화를 나타내지만 관찰의 시간 척도에 따라 다른 모습을 갖는 "S" 곡선을 설명합니다.그것은 또한 이제 ^[31]다른 분야들 중에서 혁신, 조직 행동 및 그룹 학습의 관리와 관련된 복잡한 시스템에서 반복적인 균형 및 다른 종류의 혁명적인 변화에 대한 진화 이론과 관련이 있습니다.이러한 새로운 형태의 급속한 프로세스는 시스템 자체 내에서 복잡한 학습을 통해 발생하는 것으로 보이며, 관찰 가능한 경우 가속 및 감속되는 변화하는 속도의 곡선을 표시합니다.

일반적인 학습 한계

경험 곡선이라고도 불리는 학습 곡선은 일반적으로 자원과 기술에 대한 자연적 한계라는 훨씬 더 광범위한 주제와 관련이 있습니다.이러한 한계는 일반적으로 프로세스나 제품을 완벽하게 수행하거나 ^[32]측정을 완벽하게 수행하는 것에 대한 잘 알려진 한계와 같이 일을 더 효율적으로 수행하는 방법에 대한 학습을 늦추는 복잡성의 증가로 나타납니다.이러한 실제 경험은 일반적으로 폐기물 감소 한계에 대한 열역학 제2법칙의 예측과 일치합니다.폐기물을 제거하기 위한 완벽한 작업의 한계에 접근하는 것은 기하학적으로 증가하는 발전 노력을 충족시키며, 학습 경험을 변화시키는 모든 요소와 보이지 않는 모든 요소에 대한 환경 척도를 제공합니다.계속해서 긍정적인 결과가 나오더라도 노력을 계속해도 일을 완성하는 것은 점점 더 어려워집니다.학습의 복잡성으로 인해 진행 속도가 느려지는 것과 같은 유형은 유용한 기술과 제품 수명 주기 관리 및 소프트웨어 개발 주기에 적용되는 수익성 있는 시장의 한계에서도 나타납니다.나머지 시장 분절이나 잠재적인 효율성 또는 효율성은 계속해서 덜 편리한 형태로 발견됩니다.

효율성과 개발 곡선은 일반적으로 두 단계의 프로세스를 따르는데, 먼저 더 쉬운 것을 찾는 것에 해당하는 큰 단계와 더 어려운 것을 찾는 작은 단계가 뒤따릅니다.그것은 학습을 더 쉽게 만드는 획기적인 발전에 이어 학습을 더 어렵게 만드는 제약 조건을 충족시키는, 아마도 중단점을 향해 가는 학습의 폭발을 반영합니다.

• 자연적 한계 이 분야의 주요 연구 중 하나는 자원 개발 또는 기타 노력에 대한 전체 시스템 한계를 지적하며 일반적으로 물리적 또는 재정적 투자 수익률 감소에 관한 것입니다.이 중 가장 많이 연구된 것은 Energy Return on Energy Invested 또는 EROEI일 수 있으며, 지구 백과사전 기사와 휴버트 곡선이라고도 불리는 OilDrum 기사 및 시리즈에서 자세히 설명했습니다.에너지를 생산하는 데 필요한 에너지는 소비된 노력과 관련하여 남은 에너지 자원을 유용하게 만드는 방법을 배우는 데 있어 우리가 겪는 어려움의 척도입니다.천연자원 한계와 투자 증가로 인해 투자된 에너지에 대한 에너지 수익률은 한동안 지속적으로 하락해 왔습니다.에너지는 자연의 것이면서 동시에 우리 자신의 주요 자원이기도 합니다.수익이 줄어드는 것은 투자를 늘리는 것이 자원을 더 비싸게 만든다는 것입니다.자연적 한계에 가까워짐에 따라 쉽게 사용되는 소스는 고갈되고 더 복잡한 소스를 대신 사용해야 합니다.환경 신호가 지속적으로 감소하는 것처럼 EROI는 우리가 일을 실현하는 능력에 있어 전체 시스템 한계의 접근 방식을 나타냅니다.
• 유용한 자연 한계 EROEI는 투자된 노력의 수익률을 R/I 또는 학습 진행률의 비율로 측정합니다.역 I/R은 학습 난이도를 측정합니다.단순한 차이점은 R이 0에 접근하면 R/I도 0에 접근하지만 I/R은 무한대에 접근한다는 것입니다.학습 진행을 제한하는 합병증이 나타날 때 유용한 수익의 한계인 uR에 접근하고 R-uR은 0에 접근합니다.점점 더 어려워지는 작업으로 인해 유용한 학습 I/(R-uR)의 어려움이 무한대로 다가옵니다.이 지점은 특정 시점에서 지속 불가능한 노력에 의해서만 지연될 수 있는 수직 점근선으로 접근됩니다.이것은 충분한 투자가 이루어졌고 작업이 완료되는 시점을 정의하며, 보통 작업이 완료되는 시점과 동일하게 계획됩니다.계획되지 않은 작업에 대해서는 예상되거나 불시에 발견될 수 있습니다.유용성 측도인 uR은 환경 반응의 복잡성에 영향을 받으며, 이는 예측되지 않는 한 발생할 때만 측정할 수 있습니다.

문화에서

"스텝 러닝 커브"

"스텝 러닝 커브"라는 표현은 반대되는 의미로 사용됩니다.옥스포드 영어 사전, 미국 유산 영어 사전, 메리엄-웹스터 대학 사전을 포함한 대부분의 자료는 학습 곡선을 기술을 습득하는 속도로 정의하기 때문에 급격한 증가는 ^[2][33]기술의 빠른 증가를 의미합니다.하지만, 그 용어는 어려운 초기 학습 ^[3][33]과정의 의미와 함께 보통의 영어에서 자주 사용됩니다.

영어의 일반적인 용법은 곡선을 오르는 언덕으로 은유적으로 해석하기 때문입니다.가파른 언덕은 처음에는 딱딱하지만 완만한 경사면은 부담이 덜하지만 때로는 지루하기도 합니다.따라서 곡선(언덕)의 모양이 총 작업량을 나타내지 않을 수 있습니다.대신, 그것은 야망, 성격, 학습 스타일과 관련된 선호의 문제로 이해될 수 있습니다.)

• 

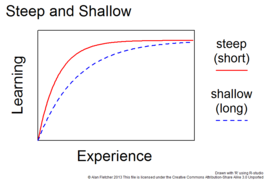
  짧고 긴 학습곡선

• 

  A 제품은 기능성이 낮고 학습 곡선이 짧습니다.B 제품은 기능은 더 뛰어나지만 학습 시간은 더 오래 걸립니다.

'쉽다'와 '어렵다'의 의미를 가진 '학습곡선'이라는 용어는 가파르고 '^[2]낮다'보다는 '짧다'와 '길다'와 같은 형용사로 설명할 수 있습니다.두 제품의 기능이 비슷하다면 더 짧은 시간에 학습할 수 있기 때문에 "급경사" 곡선을 가진 제품이 더 나을 수 있습니다.반면 두 제품의 기능이 다를 경우 곡선이 짧고(학습 시간이 짧음) 기능이 제한된 제품은 곡선이 길고(학습 시간이 길음) 기능이 큰 제품보다 좋지 않을 수 있습니다.

예를 들어 Windows(윈도우) 프로그램 메모장은 배우기가 매우 간단하지만 그 이후에는 거의 제공되지 않습니다.또 다른 극단적인 것은 유닉스 터미널 편집기 vi 또는 Vim인데, 이는 학습하기 어렵지만 사용자가 사용 방법을 배운 후에 다양한 기능을 제공합니다.

"급격한 학습 곡선 위에서"

벤 짐머(Ben Zimmer)는 20세기 초를 배경으로 한 텔레비전 시리즈인 다운턴 애비(Downton Abbey)에서 이 용어의 사용이 시대착오적인지 여부에 초점을 맞추어 이 용어의 사용에 대해 논의합니다."다운턴 수도원의 추정 상속자이자 현재 이 부동산의 공동 소유자인 매튜 크롤리는 '다운턴에 도착한 이후로 학습 곡선을 타고 있다'고 말합니다.이것은 그가 다운튼의 방식을 배우는데 어려움을 겪었다는 것을 의미하지만,^[3][34] 사람들은 1970년대까지 그런 방식으로 이야기하기 시작하지 않았습니다."

짐머는 또한 급경사를 어렵게 사용하는 것은 기술적인 의미를 뒤집는 것이라고 말합니다.그는 가파른 학습 곡선의 첫 번째 사용을 1973년으로 파악하고, 고된 해석을 1978년으로 파악합니다.

비디오 게임의 난이도 곡선

곡선을 배우는 개념은 종종 비디오 게임 게임 플레이로 번역되는데, 이것은 플레이어가 게임을 진행하면서 게임이 얼마나 어려워질 수 있는지를 설명하고 플레이어가 게임에 더 능숙해지도록 요구하며, 게임의 메커니즘을 더 잘 이해하도록 요구합니다.그리고/또는 그 또는 그녀의 인격을 향상시키기 위해 시간을 "더 많이" 소비합니다.올바른 난이도 곡선을 설정하는 것은 타이틀 내에서 게임 균형을 달성하는 것의 일부입니다.교육 환경에서 학습 곡선과 마찬가지로, 난이도 곡선은 다양한 모양을 가질 수 있으며, 게임은 게임을 더 어렵거나 ^[35][36]쉽게 만들기 위해 기본값에 비해 이 곡선의 모양을 바꾸는 다양한 난이도를 자주 제공할 수 있습니다.최적으로 비디오 게임의 난이도는 플레이어 능력과 일치하여 증가합니다.게임은 너무 도전적이거나 너무 까다롭지 않거나 너무 ^[37]지나쳐서는 안 됩니다.선수들은 한 경기가 이길 수 있다고 인식되는 한 계속 경기를 할 것입니다.따라서 이것은 승리 가능성에 대한 환상으로 일컬어집니다.승리 가능성 게임에 대한 환상을 생성하기 위해서는 적대적인 환경과 스토리에 의해 생성될 수 있는 갈등에 의한 내적 가치(목표를 향해 나아가고 그에 대한 보상을 받는 감각)가 포함될 수 있습니다.후자는 경기 ^[38]진행에 중추적인 역할을 하지 않습니다.게임 설계자들은 예를 들어, 자원을 제한함으로써 게임 플레이에 변화를 줄 수도 있습니다.한 가지 관점은 만약 플레이어들이 비디오 게임 세계가 진짜라고 믿게끔 속지 않는다면 - 세상이 활기차다고 느끼지 않는다면 -^[39][40] 게임을 만드는 것은 의미가 없다는 것입니다.

참고 항목

• 망각곡선
• 학습속도
• 노동생산성
• 학습별(경제학)
• 인구 증가
• 시행착오

참고문헌

외부 링크

• 학습곡선