달 이론

달 이론은 달의 움직임을 설명하려고 한다.달의 움직임에는 많은 작은 변화(또는 섭동)가 있으며, 그것들을 설명하기 위한 많은 시도들이 있었다.수세기 동안 문제가 됐던 달 운동은 이제 매우 높은 정확도로 모델링될 수 있습니다(현대 발전 섹션 참조).

달 이론에는 다음이 포함됩니다.

• 일반 이론의 배경: 달의 움직임을 분석하고 공식과 움직임을 예측하는 알고리즘을 생성하는 데 사용되는 수학적 기술을 포함한다.
• 일정 시간 동안 달의 위치를 계산하는 데 사용될 수 있는 정량적 공식, 알고리즘 및 기하학적 도표; 종종 알고리즘에 기초한 표의 도움을 받아.

달 이론은 2000년 이상의 연구 역사를 가지고 있다.그 보다 현대적인 발전은 지난 3세기 동안 근본적인 과학적, 기술적 목적을 위해 사용되어 왔고, 여전히 그러한 방식으로 사용되고 있다.

적용들

달 이론의 적용 분야는 다음과 같다.

• 18세기에, 달 이론과 관측 사이의 비교는 달의 원점 운동으로 뉴턴의 만유인력의 법칙을 시험하기 위해 사용되었다.
• 18세기와 19세기에, 처음에는 항해 연감에서, 달 이론에 기초한 항해표는 달 거리 방법에 의한 바다에서의 경도 결정에 많이 사용되었다.
• 매우 20세기 초에, 수성 근일점 운동의 잘 알려진 불일치는 뉴턴의 역제곱 법칙에서 -2의 힘의 부분 조정에 의해 설명될 수 있다는 사이먼 뉴콤의 제안을 시험하기 위해 달 이론과 관찰 사이의 비교가 중력 이론의 또 다른 테스트에서 사용되었습니다.중력의^[1] 차이(나중에 일반 상대성 이론에 의해 성공적으로 설명됨)
• 원자시계가 개발되기 전인 20세기 중반, 달 이론과 관측은 평균 태양시간의 불규칙성으로부터 자유로운 천문학적 시간 척도(에페메리스 시간)를 구현하기 위해 함께 사용되었다.
• 20세기 후반과 21세기 초에, 달 이론의 현대적 발전은 일반 상대성 이론과 관련된 물리적 관계의 정확성을 테스트하기 위해 고정밀 관측과 함께, Jet Propulsion Laboratory Development Ephemeris 시리즈의 태양계 모델에 사용되고 있습니다.강력한 등가 원리, 상대론적 중력, 측지학적 세차 운동, 그리고 중력 ^[2]상수의 항상성.

역사

달은 수천 년 동안 관찰되어 왔다.이러한 연령에 걸쳐, 언제든지 이용 가능한 관찰 기법에 따라 다양한 수준의 관리 및 정밀도가 가능해졌다.그에 상응하는 긴 달 이론의 역사가 있습니다: 그것은 바빌로니아와 그리스 천문학자들의 시대부터 현대의 달 레이저 범위까지 확장됩니다.

달 이론과 관련된 이름들을 가진 유명한 천문학자들과 수학자들 중에는 다음과 같은 것들이 있습니다.

바빌로니아/칼딘

• 나부리만누
• 키디누
• 사우딘

그리스어/헬레니즘

• 히파르코스
• 프톨레마이오스

아랍

• 이븐 알 샤티르

유럽, 16세기에서 20세기 초반

• 티코 브라헤
• 요하네스 케플러
• 제레미아 호록스
• 이스마엘 불랄두스
• 존 플램스티드
• 아이작 뉴턴
• 에드먼드 핼리
• 레온하르트 오일러
• 알렉시스 클레어
• 장 달랑베르
• 토바이어스 메이어
• 요한 토바이어스 뷔르크
• 피에르시몽 라플라스
• 필리프 르 둘체
• 요한 카를 부르크하르트
• 피터 안드레아스 한센
• 샤를 유겐 들뢰네
• 존 카우치 애덤스

북미, 19세기에서 20세기 초반

• 사이먼 뉴컴
• 조지 윌리엄 힐
• 어니스트 윌리엄 브라운
• 월리스 존 에커트

다른 유명한 수학자들과 수학 천문학자들 또한 상당한 기여를 했다.

역사는 세 부분으로 나눌 수 있다: 고대부터 뉴턴까지; 고전 물리학의 시대; 그리고 현대 발전.

고대 뉴턴에게

바빌론

바빌로니아 천문학에서 1880년대 ^[3]이전에는 과학사학자들에게 알려진 것이 거의 없었다.플리니의 고대 문헌에서 살아남은 사람들은 메소포타미아에 있는 세 개의 천문 학파 – 바빌론, 우루크, 그리고 '히파레눔' (아마도 '시파르')^[4]에 대해 언급하였다.그러나 세부 사항에 대한 확실한 현대 지식은 조셉 에핑이 바빌로니아 기록 보관소에서 점토판에 있는 쐐기형 문자를 해독했을 때 시작되었다.이 문서들에서 그는 ^[5]달의 위치에 대한 덧없음을 확인했다.그 이후로, 아직 단편적인 이 주제에 대한 지식은 주로 숫자 형태로 바빌론과 우루크에서 나온 서판에 있는 해독된 문서들을 면밀히 분석함으로써 쌓아야 했다(플리니가 언급한 세 번째 학파의 어떤 흔적도 아직 발견되지 않았다).

바빌로니아의 천문학자 키딘누(그리스어 또는 라틴어로, 키데나스 또는 시데나스)는 달이 고정된 별들의 배경에 대한 상대적인 경로를 따라 계속해서 속도가 변하는 것을 고려하여, 현재 "B계"라고 불리는 것의 발명이라고 여겨져 왔다.이 시스템은 달 속도의 ^[6]매일 단계적 변화를 대략 매달 최소값과 최대값으로 계산하는 것을 포함했다.이러한 시스템의 기초는 기하학적이라기보다는 산술적이었던 것으로 보이지만, 그것들은 현재 중심 방정식으로 알려진 달의 주요 부등식을 대략적으로 설명했습니다.

바빌로니아인들은 수백 년의 초승달과 ^[7]일식에 대해 매우 정확한 기록을 가지고 있었다.기원전 500년과 기원전 400년 사이의 어느 시기에 그들은 현재 메톤 ^[8]주기라고 알려진 음력과 태양년 사이의 19년 주기적 관계를 확인하고 사용하기 시작했다.

이것은 달 운동의 주요 불규칙성에 대한 수치 이론을 구축하는 데 도움을 주었고, 달 운동의 세 가지 가장 두드러진 특징의 (다른) 시기에 대해 놀랄 만큼 좋은 추정치에 도달했다.

• 달의 위상에 대한 평균 기간인 시노딕 달.현재 "계 B"라고 불리는 이 계는 각 시간 도수가 별의 겉보기 운동의 1도 또는 4분이고 세미콜론 뒤의 60진수 값은 시간 도수의 분수인 29일 및 (성별적으로) 3,11;0,50 "시간 도"로 간주합니다.이 값은 29.530594일^d = 29^hm 12 44^s 3.^[9]33으로 변환되어 29.530589일 또는^d 29^hm 12 44 ^[10]2^s.9의 현대 값(1900년 1월 0일 기준)과 비교됩니다.이 같은 값은 히파르코스와 프톨레마이오스에 의해 사용되었고, 중세 내내 사용되었으며, 여전히 히브리 달력의 기초를 형성하고 있습니다.
• 13° 10º 35º로 추산한 항성에 대한 평균 달 속도는 27.321598일로,^[11] 13° 10º 35.0275º 및 27.321582일의 ^[10]현대 값과 비교된다.
• 달의 별에 대한 이동 속도가 약 월마다 가속 및 감속되는 평균 기간인 이 비정상 달은 바빌로니아에서 27.5545833일로 ^[12][10]추정되며, 이는 현대의 27.554551일과 비교된다.
• 그draconitic 달, 달의 별들을 배경으로 경로를 먼저 확장 북쪽과 남쪽 황도 위도로 태양의 황도 경로에 비해 벗어나는 평균 기간 즉 다른 변수들 여러가지 판단에 이르는 번호로, 같은.로 지정되었다 27.212204 days,[13]27.212221를 현대적인 가치와 비교할.,[10]bu바빌로니아인들은 또한 5458개의 시노드 달이 5923개의 드라코니트 ^[13]달과 동일하다는 수치적 관계를 가졌고, 이는 시노드 달의 정확한 값과 비교했을 때 실질적으로 시노드 달의 현대적 수치로 이어진다.

히파르코스, 프톨레마이오스, 그리고 중세 작가들에 의해 2천년의 대부분 동안 바빌로니아식 추정치가 채택되었다 (그리고 그것은 여전히 계산된 히브리 달력의 기초의 일부로 사용되고 있다.

그리스와 헬레니즘의 이집트

그 후, 비티니아와 프톨레마이오스의 시대 히파르코스와 프톨레마이오스로부터 17세기 뉴턴의 작품 시대에 이르기까지, 달 이론은 주로 기하학적 아이디어의 도움으로 구성되었고, 달의 긴 일련의 위치 관측에 의해 다소 직접적으로 영감을 받았다.이러한 기하학적 달 이론에서 두드러지는 것은 원형 운동의 조합이었다 – 에피사이클 ^[14]이론의 적용이다.

히파르코스

작품이 대부분 사라졌고 주로 다른 저자들의 인용을 통해 알려진 히파르코스는 달이 황도에 대해 5° 기울어진 원 모양으로 움직이며 (즉, 태양과 달의 연간 및 월별 겉보기 운동 방향과는 반대) 역행 방향으로 18년에 한 번 회전한다고 가정했다.2년 반 3년이 원은 달이 역행하는 것으로 추정되는 에피사이클을 운반하는 변종 역할을 했다.에피사이클의 중심은 달의 경도 평균 변화에 해당하는 속도로 움직였고, 에피사이클 주변의 달 주기는 비정상적 달이었다.이 에피사이클은 타원 부등식, 중심 방정식 및 중심 방정식 약 5°1'에 가까운 크기를 대략적으로 제공하였다.이 수치는 현대 값보다 훨씬 작습니다: 그러나 중심 방정식의 현대 계수(1항)와 전야 방정식의 차이에 가깝습니다: 그 차이는 일식 시간에 고대 측정이 이루어졌다는 사실과 전야 효과에 의해 설명됩니다.중심 방정식의 e 조건)은 당시 알려지지 않았고 간과되었다.상세한 것에 대하여는, 별도 기사 「이브레이션」을 참조해 주세요.

프톨레마이오스

프톨레마이오스의 업적 알마게스트는 천 년 이상 폭넓고 오랫동안 받아들여지고 영향을 끼쳤다.그는 달의 움직임의 두 번째 부등식을 제공함으로써 히파르코스보다 개선된 기하학적 달 이론을 제시했고, 겉으로 보이는 원점인 에피시스를 약간 진동시키는 장치를 사용했다.이 두 번째 부등식 또는 두 번째 변칙은 중심 방정식뿐만 아니라 전야로 알려지게 된 것에 대해서도 대략적으로 설명되었습니다.그러나 이 이론은 논리적인 결론에 적용되어 달의 거리(그리고 겉보기 직경)가 2배 정도 차이가 나는 것처럼 보일 것이며,^[15] 이는 분명히 현실에서 볼 수 없는 것이다.(달의 외관상 각지름은 매월 달라지지만, 훨씬 좁은 범위인 약 0.49°~0.55°^[16]에 불과하다.)프톨레마이오스 이론의 이러한 결함은 14세기에는^[17] 이븐 알 샤티르에 의해 그리고 ^[18]16세기에는 코페르니쿠스에 의해 대체될 것을 제안했다.

이븐 알 샤티르와 코페르니쿠스

달 이론의 중요한 발전은 아랍의 천문학자 이븐 알 샤티르 (1304–1375)에 의해 이루어졌다.달까지의 거리가 프톨레마이오스의 달 모형에서 요구하는 것만큼 급격하게 변하지 않았다는 관측을 바탕으로,^[17][19] 그는 프톨레마이오스의 크랭크 메커니즘을 지구에서 달의 계산된 거리 범위를 줄인 이중 에피사이클 모형으로 대체한 새로운 달 모형을 만들었다.르네상스 천문학자 니콜라우스 코페르니쿠스에 의해 약 150년 후에 개발된 유사한 달 이론은 달 ^[20][21]거리에 관해 같은 이점을 가지고 있었다.

티코 브라헤, 요하네스 케플러, 제레미아 호록스

이 섹션은 어떠한 출처도 인용하지 않습니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 섹션의 개선에 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.(2012년 5월) (이 템플릿메시지 삭제 방법 및 삭제 타이밍에 대해 알아보기)

티코 브라헤와 요하네스 케플러는 프톨레마이오스 달 이론을 다듬었지만 달의 거리, 겉보기 지름, 시차에서 (주로 매달) 변화를 제대로 설명하지 못하는 중심적인 결함을 극복하지 못했다.그들의 연구는 달 이론에 세 가지 실질적인 발견을 더했다.

1. 노드와 달 궤도면의 기울기는 둘 다 (타이코에 따르면) 매달 또는 (케플러에 따르면) 반년 주기로 사행하는 것으로 보인다.
2. 달 경도는 달이 초승달과 보름달에 예상보다 빨리 움직이고, 분기마다 예상보다 느리게 움직이는 두 달마다 변동이 있다.
3. 또한 1월에는 달의 움직임이 약간 느려지고 7월에는 약간 빨라지는 연간 효과도 있다: 연차 방정식.

브라헤와 케플러의 정교함은 그들의 직계 후계자들에 의해 개선으로 인식되었지만, 그들의 17세기 후계자들은 문제를 더 개선하기 위해 달의 움직임을 위한 수많은 대체 기하학적 구성을 시도했다.주목할 만한 성공은 제레미아 호록스에 의해 이루어졌는데, 호록스는 달의 원점 위치 및 타원 편심 크기에서 약 6개월의 자전을 포함하는 계획을 제안했다.이 계획은 달의 거리, 지름, 시차의 변화를 보다 사실적으로 묘사하는 데 큰 장점이 있었다.

뉴턴 경이다.

달 이론의 첫 번째 중력 시기는 뉴턴의 작품에서 시작되었다.그는 달의 교란운동의 문제를 현대적 용어로 정의한 최초의 인물이다.그의 획기적인 작품은 1687년에 출판된 초판을 포함한 모든 판본에서 프린키피아에^[22] 소개되어 있다.

달 운동의 태양 섭동

뉴턴은 제1권, 제66호,^[23] 제3권,^[24] 제25호에서 지구와 달의 상대적인 운동에 대한 교란 효과를 평가하는 방법을 알아냈다.이 접근방식의 출발점은 운동의 ^[25]법칙에 대한 결과 VI입니다.이것은 어떤 거대한 물체의 외부 가속력이 고려된 다른 물체에 동등하고 병렬로 작용한다면, 그 물체는 똑같이 영향을 받을 것이고, 그 경우 (서로 상대적인) 그들의 움직임은 마치 그러한 외부 가속력이 전혀 없는 것처럼 계속될 것이라는 것을 보여준다.외부 힘(예: 제1권, 제66호, 제3권, 제25호, 태양에 대한 중력)이 고려되는 다른 물체에 대한 가속 효과의 크기 또는 방향이 다른 경우에만, 그 결과 발생하는 영향은 L의 상대적인 운동에 주목할 수 있다.시체들(뉴튼은 태양과 같은 외부의 거대한 유인력에 의한 가속력 또는 가속 중력을 가리켰다.그가 사용한 척도는 현재 우리가 힘 그 자체라고 부르는 것보다 힘이 만들어 내는 경향이 있는 힘을 말한다면, 단위 질량 당 힘).

따라서 뉴턴은 지구에 대한 달의 움직임을 방해하는 것은 달에 대한 태양의 가속력과 지구에 대한 태양의 인력 사이의 차이일 뿐이라고 결론지었다.

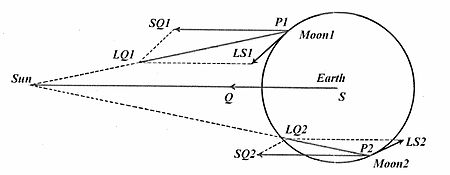
뉴턴은 실제로 이 분석을 수행하기 ^[26]위해 힘의 벡터 분해를 이용했다.제1권, 제66권, 제3권,^[27] 제25권에서는 지구의 태양과 달의 총중력에서 출발하는 기하학적 구조를 통해 지구에 대한 달의 움직임에 대한 교란 효과를 나타내는 차이를 보여주었다.요약하면, 아래 그림과 같이 뉴턴의 다이어그램에서 선 LS는 달의 현재 위치 P에서 달에 작용하는 교란 가속도의 크기와 방향을 나타낸다(선 LS는 점 P를 통과하지 않지만, 텍스트는 이것이 유의하지 않다는 것을 보여준다. 이는 스케일 팩터와 다이어그램이 작성된 방식에 따른 결과이다).tup)을 클릭합니다.

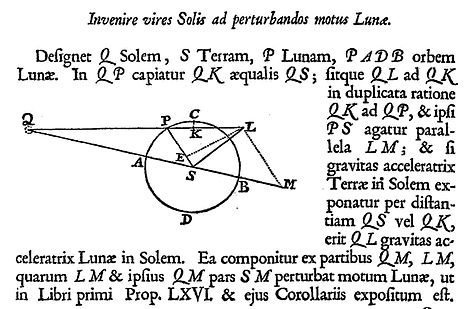
여기에 표시된 것은 프린키피아 제1판(1687)의 라틴판 (제3권, 제25호, 페이지 434)의 뉴턴의 도표입니다.여기서 그는 태양-지구-달 시스템에서 달에 대한 교란 가속에 대한 분석을 소개했다.Q는 태양, S는 지구, P는 달을 나타냅니다.

이 다이어그램의 일부는 거리, 다른 부분은 중력 가속도(단위 질량당 인력)를 나타냅니다.이중 유의에서, SQ는 지구-태양 거리를 나타내며, 또한 지구-태양 중력 가속도의 크기와 방향을 나타냅니다.다이어그램의 다른 거리는 거리 SQ에 비례합니다.다른 볼거리는 볼거리 SQ에 비례합니다.

태양의 매력은 SQ와 LQ이다.LQ의 크기는 LQ의 유인 비율이 다음과 같이 되도록 그려집니다.SQ는 거리 PQ 비율의 역제곱입니다.SQ.(Newton은 비율을 보다 쉽게 볼 수 있도록 KQ=SQ를 구성합니다.)달에 대한 지구의 인력은 PS 방향을 따라 작용한다. (그러나 PS선은 지금까지 거리와 방향만을 나타내며, 태양과 지구의 인력 사이의 스케일 팩터에 대해 정의된 것은 없다.)

뉴턴은 달에서 LQ를, 지구에서 SQ를 같은 척도로 나타낸 뒤 LQ를 LM과 MQ로 벡터 분해한 뒤 달에서의 교란가속도를 SQ와의 차이로 파악한다.SQ와 MQ는 서로 평행하므로 MQ에서 직접 SQ를 빼서 MS를 남길 수 있습니다. 따라서 LQ에서 SQ를 뺀 후의 차이는 LM과 MS의 벡터 합이 됩니다.이러한 합계는 교란 가속 LS가 됩니다.

나중에 뉴턴은 LM+MS = LS의 또 다른 분해능을 직교 성분, 즉 LE와 평행한 가로 성분과 효과적으로 ES인 방사 성분으로 확인하였다.

뉴턴의 도표는, 그의 시대 이후, 다른 그리고 어쩌면 시각적으로도 명확한 방식으로 다시 제시되었다.여기에 표시된 것은 지구 궤도에 있는 달의 P1과 P2의 두 가지 다른 위치에 대해 태양에 의한 교란 가속에 대한 각각의 벡터 LS1과 LS2를 나타내는^[28] 벡터 표시이다.P1에서의 달의 위치는 뉴턴의 다이어그램에서 P에서의 위치와 상당히 비슷하며, 대응하는 섭동 LS1은 크기와 방향에서 뉴턴의 LS와 같다.또 다른 위치 P2에서는 달이 지구보다 태양에서 더 멀리 떨어져 있고, 달에 대한 태양의 인력 LQ2는 지구에 대한 태양의 인력 SQ=RQ2보다 약하며, 그 결과 발생하는 섭동 LS2는 태양에서 비스듬히 떨어져 있다.

뉴턴의 도표와 같은 구조들은 궤도에 있는 달의 많은 다른 위치에 대해 반복될 수 있다.각 위치에서 결과는 두 번째 다이어그램의 LS1 또는 LS2와 같은 섭동 벡터이다.여기 보이는 것은 자주 나타나는 다이어그램의 형태이며, 궤도 내 달의 다양한 위치에 대한 섭동 벡터의 크기와 방향을 요약합니다.각각의 작은 화살표는 LS와 같은 섭동 벡터이며, 화살표가 시작되는 궤도 주변의 특정 위치에 있는 달에 적용할 수 있습니다.달이 지구-태양 축을 따라 거의 일직선에 있을 때, 즉 초승달이나 보름달 가까이 있을 때, 달은 지구로부터 바깥쪽으로 방향을 잡습니다.달-지구 선이 지구-태양 축에서 90°일 때, 그들은 안쪽, 지구를 가리키며, 크기는 축 방향(외부) 섭동의 최대 크기의 절반에 불과합니다.(뉴튼은 태양 교란력의 크기에 대해 꽤 좋은 양적 추정을 했다: 지구의 매력을 더하는 직교에서 그는 지구의 평균 지구 인력 중 1⁄178.725, 그리고 지구의 인력에 반대하여 감소시키는 초승달과 보름달의 두 배에 달하였다.)^[27]

뉴턴은 또한 같은 섭동의 패턴이 태양에 의해 교란되는 지구에 대한 관계뿐만 아니라 태양에 의해 교란되는 고체 지구에 대한 관계에서도 더 일반적으로 적용된다는 것을 보여주었다. 예를 들어 지구 표면의 다른 ^[a]조수 부분들.이러한 교란 가속의 일반적인 패턴에 대한 연구는 달의 섭동에 대한 뉴턴의 초기 연구에서 비롯되었으며, 그는 또한 조수를 움직이는 힘에도 적용했습니다.오늘날 이러한 일반적인 패턴 자체가 달의 움직임이나 지구의 조수 또는 유사한 패턴의 섭동을 겪는 다른 물체의 움직임의 방해에 적용되는지 여부에 관계없이 종종 조력이라고 알려져 왔다.

제3권 발의안 제25호에서 '달을 교란시키는 태양의 힘을 찾기 위해'라는 도표를 소개한 후, 뉴턴은 달이 지구를 한 바퀴 돌면서 그 성분이 어떻게 변하는지 더 자세히 보여주면서 태양 교란력에 대한 최초의 근사치를 개발했다.그는 또한 달 ^[b]움직임의 불규칙성을 만들어냄으로써 교란력이 어떻게 그 효과를 나타내는지 조사하는 첫 단계를 밟았다.

선택된 몇 개의 달 부등식에 대해, 뉴턴은 그것들이 태양 교란력으로부터 어떻게 생기는지를 양적으로 상세하게 보여주었다.

뉴턴의 이러한 달 작업의 대부분은 1680년대에 이루어졌고, 중력 분석에서 그의 첫 단계의 범위와 정확성은 여러 요인에 의해 제한되었다. 여기에는 전체적으로 어려운 기하학적 방법으로 작업을 개발하고 제시하는 그의 선택과 많은 천문학적인 측정의 제한된 정확성과 불확실성에 의해 제한되었다.그의 시대의 변화.

뉴턴 이후의 고전 중력 주기

18세기 중반 레온하르트 오일러, 알렉시스 클레로, 장 달랑베르에서 19세기 후반과 20세기 초 E.W. 브라운에 이르기까지 뉴턴의 후계자들의 주요 목표는 뉴턴의 법칙과 중력 법칙에 기초해 달의 움직임을 완전하고 정확하게 설명하는 것이었다.끌어당기는 물체 사이의 거리 제곱에 반비례하는 끌어당기는 것에 의해.그들은 또한 역제곱 중력의 법칙을 실험하기를 원했고, 1740년대에 그것은 심각하게 의심받았는데, 그 이유는 달의 원점 운동에서 뉴턴 이론과 관측된 비율 사이의 큰 불일치로 생각되었기 때문이다.그러나 클레어는 얼마 지나지 않아 (1749–50) 뉴턴의 법칙에 기초한 달 이론이 아니라 그와 다른 사람들이 그것을 평가하기 위해 의존했던 과도한 근사치에 불일치의 주요 원인이 있다는 것을 보여주었다.

뉴턴 이후 이론의 대부분의 발전은 대수적 형태로 이루어졌다: 그것들은 양적이고 매우 힘든 양의 미적분과 삼각법을 포함했다.또한 이 시기의 이론을 완성하기 위해서는 관측 ^{[29][30][31][32]}측정치를 참조할 필요가 있었다.

이론의 결과

달 이론가들은 중력 문제를 분석하기 위해 많은 다른 수학적 접근법을 사용했다.놀랄 것도 없이, 그들의 결과는 수렴되는 경향이 있었다.뉴턴의 후계자인 오일러, 클레로, 달랑베르 중 가장 초기의 중력 분석가들이 있던 시기부터, 거의 모든 주요 달 섭동은 단지 몇 개의 각도 논쟁과 계수로 표현될 수 있다는 것이 인식되었다.이는 다음과 ^[32]같이 나타낼 수 있습니다.

• 달과 태양의 평균 운동 또는 위치와 함께 3개의 계수 및 3개의 각도 위치를 나타내며, 이들은 함께 겉보기 궤도의 모양과 위치를 정의합니다.
• 달과 태양의 겉보기 궤도에 근접하는 타원형의 두 가지 이심률$($$e\displaystyle$e\, 약 0.0549) 및 $\\$ e$\backslash ,$ 약 0.01675)
• 두 궤도의 근지점(${\displaystyle \mathrm{}}$ \$displaystyle \Gamma)$ 및$($ their $\$$displaystyle \Gamma$의 각도 방향(또는 원지점)
• 두 궤도의 평면 사이의 기울기 각도$($$displaystyle$$$i), 평균값 약 18523")와 두 평면이 교차하는 노드 선의 방향$(δ$ \$displaystyle$ \Omega$）.$상승 노드($\style$ \$Omega$ $\}$ )는 달이 황도에 대해 북쪽으로 기울 때 통과하는 노드입니다.

이러한 기본 매개변수로부터, 단지 4개의 기본 미분 각도 인수는 달 운동의 거의 모든 유의한 섭동을 다른 조합으로 표현하기에 충분하다.그것들은 델라우나이 때문에 기존의 기호와 함께 여기에 주어집니다.때로는 델라우나이 주장으로 알려져 있습니다.

• ${\displaystyle l}${\$displaystyle$$l}$ 달의$$ 평균 이상(달 근지점$\delta$의 평균 경도에서 달의 평균 경도의 각도 $거리$)$$
• ${\displaystyle l^{}}$anomaly { $displaystyle$ l$$}태양의$$ $평균경도{\displaystyle {\mathrm{}}^{}}$ ${\$ { $displaystyle$\ $Gamma$'${\displaystyle {}^{}}$}$$ ′ ′ l′ l l 。
• ${\displaystyle F}${\$displaystyle$ $F}$ 달의$$ 평균 위도 인수(달의 상승(북향) 노드$\delta$의 평균 경도에서 달의 평균 경도의 각도 $거리$)$$
• $\displaystyle D$: 달의 평균(태양의 평균 경도에서 달의 평균 경도의 각도) 연장.

이 작업은 브라운의 달 이론과 ^{[33][34][35][36][37]}달 운동의 표로 정점에 도달했다.^[31]이것들은 1968년까지 American Ephemeris와 Nairy Almanac에 사용되었고 1984년까지 수정된 형태로 사용되었습니다.

가장 크거나 명명된 달의 부등식

경도에서 가장 큰 달 섭동들 중 몇 개가 명명되었다(평균 경도에 대한 실제 황도 경도의 차이에 대한 기여).미분 인수에 관해서는 계수를 원호의 가장 가까운 초(")^[38]로 반올림하여 다음과 같은 방법으로 표현할 수 있습니다.

중심 방정식

• 달의 중심 방정식, 즉 타원 부등식은 적어도 바빌로니아와 히파르코스 이후의 고대인들에게는 대략적으로 알려져 있었다.보다 최근의 지식은 타원 궤도에서 동일한 면적에 대한 케플러의 법칙의 대략적인 적용에 해당하며, 달이 근지점 쪽으로 이동하는 동안 지구로부터의 거리가 줄어들고, 그리고 지구로부터의 거리가 이동하는 동안 속도가 느려지는 것을 나타낸다.그 원점달의 경도에 대한 효과는 일련의 항으로 근사할 수 있으며, 그 중 처음 3개는${\displaystyle }$+${\displaystyle {22639}^{}\sin }$ sin ${\displaystyle (}$ (${\displaystyle l}$) + ${\displaystyle {769}^{}\sin }$ sin$$ ( ${\displaystyle 2l}$) + ${\displaystyle {36}^{}}$ sin ${\displaystyle (}$ ( $3$l$$) \ $displaystyle$+ $22639$" \$sin$ ( $l$ ) + $769$" + sin ( l ) + $36$ " sin ( l $)"$

이브온

• 전야제(또는 그 근사치)는 프톨레마이오스에게 알려졌지만, 그 이름과 원인에 대한 지식은 17세기부터 시작되었다.달의 경도에 미치는 영향의 주기는 약 31.8일이다.이는 여러 가지 방법으로 표현될 수 있는데, 예를 들어 근지점 위치에서 약 6개월의 자전과 함께 달의 궤도 ^[39]이심률 크기에서 6개월의 맥동이 동반된 결과이다.주요 용어는 + ${\displaystyle {4586}^{}}$ ${\displaystyle \sin {}^{}}$sin${\displaystyle }$( ${\displaystyle 2D}$ -${\displaystyle l}$ $){$ $displaystyle +4586'\sin$( 2 D -$$l )$$} 입니다.

변화

• 타이코 브라헤가 발견한 변이는 달이 초승달과 보름달에 가까워질수록 속도가 빨라지고 1분기와 지난 분기에 가까워질수록 속도가 느려진다.양적 추정을 통한 중력 설명은 뉴턴에 의해 처음 제시되었다.주요 용어는 + ${\displaystyle {2370}^{}}$ 70${\displaystyle {}^{}\sin }$( ${\displaystyle 2D}$) ( \ $displaystyle$+ $2370$" \$sin$ ( 2 $D$)$$$。{\displaystyle }$

연차 방정식

• 브라헤가 발견한 이 연례 방정식은 지구가 1월 초에 태양과 가장 가까운 근일점에 있을 때 달의 궤도가 약간 커지고 기간이 길어지며 태양의 섭동 효과가 가장 강하며, 그 후 크기가 약간 축소되고 짧아진다는 관점에서 뉴턴에 의해 정성적으로 설명되었다.7월 초순에 태양이 가장 멀리 떨어져 있는 시간: 교란 효과가 약해지는 시간: 이 효과로 인한 주 용어의 현대 값은 ${\displaystyle {-668}^{}\sin }$ sin${\displaystyle {}^{}}$ ( l$$ ) \ $display$ - $668$" \$sin$ ( l )$$$。{\displaystyle }$

시차 부등식

• 뉴턴에 의해 처음 발견된 시차 부등식은 태양의 유한한 거리와 0이 아닌 시차로 인해 브라헤의 변화를 약간 비대칭으로 만듭니다.그 효과는 달이 1분기에는 조금 뒤처지고, 4분기에는 조금 앞섰다는 것이다.이것의 주요 용어는 - ${\displaystyle {125}^{}}$ ${\displaystyle \sin }$sin (${\displaystyle D}$) \ $displaystyle$ - $125$" \$sin$ ( D )$。$

황도 감소

• 황도로의 감소는 달의 움직임을 황도 평면에서 경도로 표현하는 기하학적 효과를 나타내지만, 달의 움직임은 실제로 약 5도 기울어진 평면에서 일어나고 있다.주요 용어는 - ${\displaystyle {412}^{}}$ ${\displaystyle \mathrm{12}\sin }$ ($$2${\displaystyle }$F ) \ $displaystyle$ - $412$" \$sin$ ( 2$F$ ) $。$

18세기 중반의 분석가들은 약 25-30개의 삼각법을 사용하여 경도에서 달의 위치에 대한 섭동을 표현했다.하지만, 19세기와 20세기의 연구는 이론의 매우 다른 공식으로 이어졌고, 그래서 이 용어들은 더 이상 현재에 존재하지 않는다.20세기 초에 달의 위치를 정확하게 표현하기 위해 필요한 용어의 수는 1400개 이상이었고, 레이저 범위 관측에 기초한 현대 수치 적분의 정확성을 모방하기 위해 필요한 용어의 수는 수만 개에 이른다: 용어의 수 증가에는 제한이 없다.정확도 요건이 ^[40]증가할수록 감소합니다.

근대적 발전

디지털 컴퓨터와 달 레이저 거리 측정

2차 세계대전 이후, 그리고 특히 1960년대 이후, 달 이론은 다소 다른 방식으로 발전해 왔다.이것은 두 가지 방법으로 자극되었다. 하나는 자동 디지털 계산의 사용이고 다른 하나는 현대 관측 데이터 유형에 의해 정확성과 정밀도가 크게 향상되었다.

어니스트 윌리엄 브라운의 제자이자 IBM의 직원인 월러스 존 에커트는 2차 세계대전 이후 그곳에서 개발된 실험용 디지털 컴퓨터를 천문학적 순간이동체 계산에 사용했습니다.그 프로젝트들 중 하나는 브라운의 달 이론을 기계에 넣고 표현들을 직접 평가하는 것이었다.또 다른 프로젝트는 완전히 새로운 것이었다: 태양과 4대 행성을 위한 운동 방정식의 수치적 통합이었다.이것은 전자 디지털 컴퓨터가 보급된 후에야 가능해졌다.결국 제트추진연구소 개발 에페메리스 시리즈로 이어졌다.

한편, 브라운의 이론은 더 나은 상수와 에피메리스 시간의 도입, 그리고 이와 관련된 경험적 수정의 제거로 개선되었다.이것은 달 착륙 임무가 가능하게^[41][c] 된 천문 연감에 약간의 연속적인 개선과 함께 사용되었던 개선된 ^[32]달 착륙으로 이어졌다.

달의 위치 관측에 있어 가장 중요한 개선은 지구를 묶은 레이저와 달 표면에 배치된 특수 역반사기를 사용하여 얻은 달 레이저 거리 측정이다.레이저 빛의 펄스가 역반사체 중 하나와 역반사체 중 하나에 도달하는 시간은 그 당시 달의 거리를 측정해 준다.현재 작동 중인 5개의 역반사체 중 첫 번째는 1969년 7월 아폴로 11호 우주선에 실려 달에 도착했으며 버즈 알드린에 ^[42]의해 달 표면에 적절한 위치에 배치되었다.2005년에 설립된 Apache Point Observatory Lunar Laser-range Operation에 의해 정밀도가 더욱 확대되었습니다.

수치 적분, 상대성 이론, 조류, 사서

이러한 현대적 측정법을 사용하여 수치적으로 정밀하게 개발된 달 이론은 고전적인 이론보다 더 광범위한 고려사항에 기초한다.그것은 (상대론적 보정을 수반하는) 중력뿐만 아니라 많은 조석 및 지구물리학적 효과와 달의 자유에 대한 매우 확장된 이론을 고려합니다.다른 많은 과학 분야와 마찬가지로, 이 분야도 이제 대규모 팀과 기관의 작업에 기반하도록 발전했습니다.이러한 발전의 주요 부분 중 하나를 차지하는 기관은 캘리포니아 공과대학교의 제트 추진 연구소 (JPL)입니다; 그리고 특히 1970년대 초반부터, 고전적인 달 이론과 현대 과학 상태로의 덧없음으로의 전환과 관련된 이름들은 과학의 그것들을 포함합니다.J. Derion Mulholland와 J.G. Williams, 그리고 태양계(행성) 후천성 E의 연계 개발을 위해.마일스 ^[43]스탠디시

1970년대 이후 JPL은 Lunar Ephemerides(LExx)를 통합한 수치 통합 Development Ephemerides(DExxxx)를 생산하고 있습니다.1984~2002년 공식 천문 연감에는 행성 및 달 별자리 DE200/LE200이 사용되었으며,^[44] 2003년호부터는 정확도와 정밀도가 한층 향상된 별자리 DE405/LE405가 사용되고 있다.현재 사용후기는 DE440입니다.^[45]

분석 개발

이러한 발전과 병행하여, 최근 몇 년 동안 분석적인 달 이론의 새로운 클래스가 개발되었으며, 특히 장 샤프론트와 미셸 샤프론투제(Bureau des Longratitudes)의 에페메리드 루네르^[46] 파리지엔느(Ephemeride Lunaire Parisienne)가 있다.컴퓨터 보조 대수를 사용하여, 해석적 발전은 수작업으로 작업하는 고전적인 분석가들에 의해 이전에 수행될 수 있는 것보다 더 멀리 이루어졌다.또한 이러한 새로운 분석 이론들 중 일부는 위에서 언급한 바와 같이 JPL에서 이전에 개발된 수치 에페머라이드에 적합되었다.이러한 최근의 분석 이론의 주요 목적은, 지난 세기의 고전 이론의 목적과 대조적으로, 현재 날짜에 대한 개선된 위치 데이터를 생성하는 것이 아니라, 오히려, 그들의 목표는 현대에서 쉽게 드러나지 않을 수 있는 장기적 특성과 같은 운동의 더 많은 측면에 대한 연구를 포함했습니다.수치론 그 ^[47]자체입니다.

메모들

레퍼런스

참고 문헌

• 'AE 1871': "Nautical Almanac & Astronomical Ephemeris" for 1871, (London, 1867).
• E W Brown (1896). An Introductory Treatise on the Lunar Theory, Cambridge University Press.
• E W Brown. "Theory of the Motion of the Moon", Memoirs of the Royal Astronomical Society, 53 (1897), 39–116.
• E W Brown. "Theory of the Motion of the Moon", Memoirs of the Royal Astronomical Society, 53 (1899), 163–202.
• E W Brown. "Theory of the Motion of the Moon", Memoirs of the Royal Astronomical Society, 54 (1900), 1–63.
• E W Brown. "On the verification of the Newtonian law", Monthly Notes of the Royal Astronomical Society 63 (1903), 396–397.
• E W Brown. "Theory of the Motion of the Moon", Memoirs of the Royal Astronomical Society, 57 (1905), 51–145.
• E W Brown. "Theory of the Motion of the Moon", Memoirs of the Royal Astronomical Society, 59 (1908), 1–103.
• E W Brown (1919). Tables of the Motion of the Moon, New Haven.
• M Chapront-Touzé & J Chapront. "The lunar ephemeris ELP-2000", Astronomy & Astrophysics 124 (1983), 50–62.
• M Chapront-Touzé & J Chapront: "ELP2000-85: a semi-analytical lunar ephemeris adequate for historical times", Astronomy & Astrophysics 190 (1988), 342–352.
• M Chapront-Touzé & J Chapront, Analytical Ephemerides of the Moon in the 20th Century (Observatoire de Paris, 2002).
• J Chapront; M Chapront-Touzé; G Francou. "A new determination of lunar orbital parameters, precession constant and tidal acceleration from LLR measurements", Astronomy & Astrophysics 387 (2002), 700–709.
• J Chapront & G Francou. "The lunar theory ELP revisited. Introduction of new planetary perturbations", Astronomy & Astrophysics 404 (2003), 735–742.
• I B Cohen and Anne Whitman (1999). Isaac Newton: 'The Principia', a new translation, University of California Press. (For bibliographic details but no text, see external link.)
• J O Dickey; P L Bender; J E Faller; and others. "Lunar Laser Ranging: A Continuing Legacy of the Apollo Program", Science 265 (1994), pp. 482–490.
• J L E Dreyer (1906). A History of Astronomy from Thales to Kepler, Cambridge University Press, (later republished under the modified title "History of the Planetary Systems from Thales to Kepler").
• W J Eckert et al. Improved Lunar Ephemeris 1952–1959: A Joint Supplement to the American Ephemeris and the (British) Nautical Almanac, (US Government Printing Office, 1954).
• J Epping & J N Strassmaier. "Zur Entzifferung der astronomischen Tafeln der Chaldaer" ("On the deciphering of Chaldaean astronomical tables"), Stimmen aus Maria Laach, vol. 21 (1881), pp. 277–292.
• 'ESAE 1961': 'Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac' ('prepared jointly by the Nautical Almanac Offices of the United Kingdom and the United States of America'), London (HMSO), 1961.
• K Garthwaite; D B Holdridge & J D Mulholland. "A preliminary special perturbation theory for the lunar motion", Astronomical Journal 75 (1970), 1133.
• H Godfray (1885). Elementary Treatise on the Lunar Theory, London, (4th ed.).
• Andrew Motte (1729a) (translator). "The Mathematical Principles of Natural Philosophy, by Sir Isaac Newton, translated into English", Volume I, containing Book 1.
• Andrew Motte (1729b) (translator). "The Mathematical Principles of Natural Philosophy, by Sir Isaac Newton, translated into English", Volume II, containing Books 2 and 3 (with Index, Appendix containing additional (Newtonian) proofs, and "The Laws of the Moon's Motion according to Gravity", by John Machin).
• J D Mulholland & P J Shelus. "Improvement of the numerical lunar ephemeris with laser ranging data", Moon 8 (1973), 532.
• O Neugebauer (1975). A History of Ancient Mathematical Astronomy, (in 3 volumes), New York (Springer).
• X X Newhall; E M Standish; J G Williams. "DE102: A numerically integrated ephemeris of the Moon and planets spanning forty-four centuries", Astronomy and Astrophysics 125 (1983), 150.
• U S Naval Observatory (2009). "History of the Astronomical Almanac".
• J G Williams et al. "Making solutions from lunar laser ranging data", Bulletin of the American Astronomical Society (1972), 4Q, 267.
• J.G. Williams; S.G. Turyshev; & D.H. Boggs. "Progress in Lunar Laser Ranging Tests of Relativistic Gravity", Physical Review Letters, 93 (2004), 261101.

외부 링크

• 위키 인용의 달 이론 관련 인용문