마르코프 결정 과정

수학에서, 마르코프 결정 과정(MDP)은 이산 시간 확률 제어 과정이다.이는 결과가 부분적으로 랜덤하고 부분적으로 의사결정자의 통제 하에 있는 상황에서 의사결정을 모델링하기 위한 수학적 프레임워크를 제공한다.MDP는 동적 프로그래밍을 통해 해결된 최적화 문제를 연구하는 데 유용합니다.MDP는 적어도 1950년대에 ^[1]알려져 있었고, 1960년 로널드 하워드의 저서 동적 프로그래밍과 마르코프 ^[2]프로세스에서 비롯된 마르코프 의사결정 과정에 대한 핵심 연구 주체가 되었다.로봇 공학, 자동 제어, 경제 및 제조를 포함한 많은 분야에서 사용되고 있습니다.MDP의 이름은 마르코프 사슬의 연장선상에 있는 러시아 수학자 안드레이 마르코프에서 유래했다.

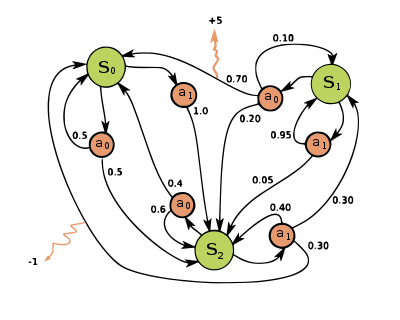
각 단계에서 프로세스는 어떤 $상태$에 있으며$,$ 의사결정자는 상태 $s에서 사용$ 가능한 $모든$ $액션$을 선택할 수 있습니다$.$프로세스는 다음 단계에서 무작위로 새로운 $상태{\displaystyle {}^{}}$ s$(\$ s$\text{'})$로 이행하여 의사결정자에게 대응하는 $보상{\displaystyle {}_{}}$ ${\displaystyle R_{}}$ ${\displaystyle a{}_{}}$( s${\displaystyle }$, ${\displaystyle {}^{}}$ ${\displaystyle )}$)(\$displaystyle$R_${a$（ s , s ; s$$; ) )를 주는 것으로 응답합니다$.$

$프로세스$가 새로운 $상태$로 이행할 확률은 선택된 액션에 의해 영향을 받습니다$.$구체적으로는 상태 전이 $함수{\displaystyle {}_{}}$ ${\displaystyle P_{}}$ a${\displaystyle {}_{}}$( ${\displaystyle s}$, ${\displaystyle {}^{}}$ ${\displaystyle )}$ $){displaystyle P_{a}(s, s')$에 의해 지정됩니다$.$따라서 다음 $상태$ s$({$ s$')$는 현재 $상태{\displaystyle }$s(\$displaystyle$ s$)$와 의사결정자의 $행동{\displaystyle }$a(\$displaystyle$ a$)$에 따라 달라집니다.단$,$ s(\$displaystyle$ s$$$)$와$$a(\$displaystyle$ a$)$를 지정하면 이전 상태 및 액션과는 조건적으로 독립적입니다.마르코프 성질을 만족시킬 수 있습니다.

마르코프 결정 과정은 마르코프 사슬의 연장선이다. 차이점은 행동(선택을 허용하는 것)과 보상(동기 부여)의 추가이다.반대로, 각 상태에 대해 하나의 작용만 존재하고(예: "대기") 모든 보상이 동일하다면(예: "제로") 마르코프 결정 과정은 마르코프 연쇄로 감소한다.

정의.

마르코프 결정 프로세스는 4-태플$({\displaystyle S,}$ ${\displaystyle A,}$ ${\displaystyle {}_{}}$ ${\displaystyle a_{}}$ $)\displaystyle(S, A, P_{a}, R_{a$입니다.

• $(\displaystyle$ S$)$는 일련의 상태를 나타냅니다.
• $\displaystyle$A는$$ \displaystyle A_${s}$라고 불리는 일련의 ${\displaystyle \mathrm{액션}}$입니다(${\displaystyle {또는}_{}}$ \$displaystyle A_${s}는 \$displaystyle$ s$}$에서 사용 가능한 액션 세트입니다).
• ${\displaystyle P_{}}$ a${\displaystyle {}_{}}$(${\displaystyle s}$ , ${\displaystyle {}^{}}$ ${\displaystyle \prime }$ ) ${\displaystyle ={Pr}_{}}$ ( ${\displaystyle s_{}}$+ ${\displaystyle 1_{}}$ $=$ ${\displaystyle {}^{}}$ ${\displaystyle {}_{}}$ ${\displaystyle s_{}}$ ${\displaystyle \mathrm{display}}$ s ${\displaystyle {}_{}}$s , ${\displaystyle {}_{}}$ ) ${\displaystyle =}$\ $displaystyle$ $P_{a$ }($s,$ s$')$= \ $Pr$( $s_{$t$+1}='s$ \ $mid$ s_${t$} =$s,a_t=a}$ } } } } $display$ style$$display display display display display display display display display display display display display display display display display display display display display display display display display display$1$(\ $displaystyle$ t$+1$)$$$,$
• ${\displaystyle R_{a}(s,s')}$ is the immediate reward (or expected immediate reward) received after transitioning from state ${\displaystyle s}$ to state ${\displaystyle s'}$, due to action ${\displaystyle a}$

상태 및 동작 공간은 유한하거나 무한할 수 있습니다(예: 실수의 집합).무한 상태 및 동작 공간을 갖는 일부 프로세스는 유한 상태 및 동작 ^[3]공간을 갖는 프로세스로 축소될 수 있습니다.

정책 함수$(\displaystyle \pi)$는 상태 공간$(\displaystyle$ S$)$에서 액션 공간(\$displaystyle$ A$)$으로의 (가능성이 있는) 매핑입니다.

최적화 목표

마르코프 의사결정 프로세스의 목표는 의사결정자가 $상태$일 때 선택할 $액션{\displaystyle }$ ${\displaystyle (}$ ( ${\displaystyle s}$) \$displaystyle$$\$$pi$($$s$$)를$$ 지정하는 함수 ${\$ \$displaystyle$\$pi$($$s )를 찾는 것입니다.이렇게 마르코프 의사결정 프로세스가 정책과 결합되면,는 각 상태의 동작을 수정하고 그 결과 발생하는 조합은 마르코프 체인처럼 동작합니다(${\displaystyle \mathrm{상태}}$ s$displaystyle \pi$(s)} 및 ${\displaystyle Pr<img\; alt="\backslash pi(s)"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/a3df25793e1e7a06faa8e939a794c8de8b4459bf"\; style="vertical-align:\; -0.838ex;\; width:4.232ex;\; height:2.843ex;">(s_{}}$t + ${\displaystyle 1_{}}$ $=$ ${\displaystyle {}_{}}$ ${\displaystyle \prime }$ ${\displaystyle s_{}}$ $s$ , ${\displaystyle a_{}}$ ${\displaystyle a}$ \$displaystyle \Pr(_{+1_mid_s$$}$$s).$${\displaystyle Pr}$( ${\displaystyle {}_{}}$ ${\displaystyle t_{}}$+ ${\displaystyle 1_{}}$ $=$ ${\displaystyle {}^{}}$ ${\displaystyle {\prime }^{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \prime }$ ${\displaystyle s_{}}$ t $=$) { $displaystyle \Pr(s_{t+1$}=$s'\mid$ s_${t$}=$s$ 마르코프 전이 행렬.

목표는 랜덤 보상의 누적 함수(일반적으로 무한대의 예상 할인액)를 최대화하는 정책$${\(\$displaystyle \pi)$을 선택하는 것이다.

${\displaystyle E}$ ${\displaystyle [\underset{t}{\overset{}{}}}$ t ${\displaystyle \underset{}{\overset{}{=}}}$ ${\displaystyle \underset{\mathrm{}}{\overset{}{0}}}$∞∞ ${\displaystyle {\gamma }^{}}$ r ${\displaystyle {r{}_{}}_{}}$ ${\displaystyle {R_{}}_{}}$a ${\displaystyle {}_{}}$ ( ${\displaystyle s_{}{}_{}{}_{}}$ , ${\displaystyle {\mathrm{s}}_{}}$t${\displaystyle }$+ 1 )$$]{ $display style$E \$left$ [ \$sum$ _ { t ${\displaystyle {}_{}}$ 0 }{ \ $infty }R _${ $a$_ { t${\displaystyle {}_{}}$} ( $s$_ {$t$ , s$$${\displaystyle {\_}_{}}$ s _ s _ {$t$ + 1 $}$$}$ \ right }$$ (${\displaystyle \mathrm{여기}}$서 $선택$)${\displaystyle s_{}}$ t${\displaystyle {}_{}}$+${\displaystyle {}_{}{1}_{}}$ ~${\displaystyle {P{}_{}}_{}}$ ${\displaystyle {a_{}}_{}}$t ( ${\displaystyle s_{}}$t , ${\displaystyle {}_t}$ +${\displaystyle {}_{}{1}_{}}$ $){$ $displaystyle s$_ {$t$ + $1$}\$sim$ P _ { $a$_ { $t$} ( $s$_ {$t$ , $s$_ {$t$ + $1$} )를 상정합니다.

여기서$$ \ $displaystyle$ \$$${\displaystyle \text{}}}$ $1$$${ $displaystyle$ 0 \ $leq \ leq$ \$leq$ \$\}$은$($는) 1에 가까운 $할인{\displaystyle \mathrm{}}$ 계수입니다(예를 들어, 일부 할인율 $r$의 $경우{\displaystyle }$ $1$=${\displaystyle 1}$/ (${\displaystyle 1}$ + r$$) { displaystyle$=$1 / ($1$+ r$$ ) } ） 。할인율이 낮으면 의사결정자는 조치를 무기한 연기하기보다는 조기에 취하는 것을 선호하게 됩니다.

위의 기능을 최대화하는 정책은 라고 불리며 보통 $"\$로 표시됩니다.특정 MDP에는 복수의 개별 최적 정책이 존재할 수 있습니다.마르코프 특성 때문에, 위에서 가정한 바와 같이 최적의 정책은 현재 상태의 함수임을 보여줄 수 있다.

시뮬레이터 모델

대부분의 경우 $이행확률{\displaystyle {}_{}}$ ${\displaystyle {분포}_{}}$인${\displaystyle {}_{}P}$a ( ${\displaystyle {}^{}}$ , s${\$ ){ $display style$P_${a$} $(s,$ s' )를 명시적으로 나타내기 어렵습니다$.$이러한 경우, 시뮬레이터는 전이 분포로부터 샘플을 제공함으로써 암시적으로 MDP를 모델링하기 위해 사용될 수 있다.암묵적 MDP 모델의 한 가지 일반적인 형태는 초기 상태에서 시작할 수 있는 일시적 환경 시뮬레이터이며, 작용 입력을 받을 때마다 후속 상태와 보상을 산출한다.이러한 방식으로 상태, 행동 및 보상의 궤적이 생성될 수 있습니다.

시뮬레이터의 또 다른 형태는 다음 상태의 샘플을 생성할 수 있는 단일 단계 시뮬레이터이며 어떤 상태와 ^[4]작용이든 보상을 받을 수 있습니다.(이것은 통계적 분류의 맥락에서 용어 생성 모델과는 다른 의미라는 점에 유의한다.)의사코드를 사용하여 표현되는 알고리즘에서는 G$(\displaystyle$ G$)$가 생성 모델을 나타내는 데 자주 사용됩니다.${\displaystyle 예}$를 들어 $표현식{\displaystyle {}^{}}$ s${\displaystyle }$、 ${\displaystyle r}$ ${\displaystyle \leftarrow }$ G${\displaystyle }$( ${\displaystyle s}$ , a$$) \ $displaystyle$s ' , r \ $gets$G ( $s$)는$$ 생성 모델로부터의 샘플링 액션을 나타낼 수 있습니다.$여기$서 s$(\displaystyle$ s$)$와 a$(\displaystyle$ a$)$는 현재 상태 및 $액션$이고 s$(\$$displaystyle$ s$')$는 새로운 상태 및$$rewa$)$입니다.rd. 일시적 시뮬레이터에 비해, 생성 모델은 궤도에서 마주치는 것뿐만 아니라 어떤 상태에서도 데이터를 생성할 수 있다는 장점이 있다.

이러한 모델 클래스는 정보 내용의 계층을 형성한다. 명시적 모델은 분포에서 샘플링을 통해 생성 모델을 생성하며, 생성 모델의 반복 적용은 일시적 시뮬레이터를 생성한다.반대 방향에서는 회귀를 통해서만 근사 모형을 학습할 수 있습니다.특정 MDP에서 사용할 수 있는 모델의 유형은 어떤 솔루션 알고리즘이 적절한지를 결정하는 데 중요한 역할을 한다.예를 들어, 다음 섹션에서 설명하는 동적 프로그래밍 알고리즘은 명시적 모델을 필요로 하며, 몬테카를로 트리 검색은 생성 모델(또는 임의의 상태에서 복사할 수 있는 에피소드 시뮬레이터)을 필요로 하는 반면, 대부분의 강화 학습 알고리즘은 에피소드 시뮬레이터만 필요로 한다.

알고리즘

유한한 상태와 동작 공간을 가진 MDP를 위한 솔루션은 동적 프로그래밍과 같은 다양한 방법을 통해 찾을 수 있다.이 섹션의 알고리즘은 유한한 상태 및 작용 공간을 가지고 명시적으로 주어진 전환 확률 및 보상 함수를 가진 MDP에 적용되지만, 기본 개념은 함수 근사 사용 등 다른 문제 클래스를 처리하도록 확장될 수 있다.

유한 상태 및 액션 MDP에 대한 최적의 정책을 계산하기 위한 표준 알고리즘 패밀리에서는 상태별로 색인화된 2개의 어레이(실제 값을 포함하는 값$V{\displaystyle }$ {\$displaystyle$ V$\}$ 및 액션을 포함하는 정책$actions{\displaystyle }$ {\$displaystyle \pi$에 대한 스토리지가 필요합니다.알고리즘의 마지막에, $「\displaystyle\pi」$에는 솔루션이 격납되어 있습니다.$또{\displaystyle }$, V${\displaystyle (s}$)(\$displaystyle$ V$(s)$에는, $스테이트$의$$「\$displaystyle$ s$」$로부터 그 솔루션을 따르는 것으로 얻을 수 있는 보상의 할인 합계(평균)가 격납됩니다.

알고리즘에는 (1) 값 업데이트와 (2) 정책 업데이트의 두 가지 단계가 있습니다. 이 단계는 추가 변경이 발생하지 않을 때까지 모든 상태에 대해 일정한 순서로 반복됩니다.둘 다 최적의 정책 및 상태 값의 오래된 추정치를 사용하여 최적의 정책 및 상태 값의 새 추정치를 재귀적으로 업데이트합니다.

${\displaystyle V(s):=\sum _{s'}P_{\pi(s)}(s,s')\left(R_{\pi(s)}(s,s')+\sum V(s')\right)}$

$\displaystyle \pi(s):=\operatorname {timemax} _{a}\left\{s'}P_{a}(s,s')\left(R_{a}(s,s')+\gamma V(s')\right\}$

순서는 알고리즘의 종류에 따라 다릅니다.또한 모든 상태에 대해 동시에 실행할 수도 있고 상태별로 실행할 수도 있으며, 다른 상태보다 더 많은 경우 일부 상태에 대해 실행할 수도 있습니다.어느 단계에서든 상태가 영구적으로 제외되지 않는 한 알고리즘은 최종적으로 올바른 ^[5]솔루션에 도달합니다.

주목할 만한 변종

값 반복

역유도라고도 하는 값 반복(Bellman 1957)에서는 $【\displaystyle \pi 】$는 사용되지 않고 $)】(\$$displaystyle$$\pi(s)】($s$$$)$의 값은 필요할 때마다${\displaystyle }$V($s)$ $내$에서 계산됩니다.${\displaystyle \S }$ (${\displaystyle s}$) \$displaystyle$$\pi ($$s$ )의$$ 계산을${\displaystyle }$V (${\displaystyle }$s$)$의 $계산$에 대입하면 결합된 단계가^{[further explanation needed]} 나타납니다.

${\displaystyle V_{i+1}(s):=\max _{a}\left\{s'}P_{a}(s,s')\left(R_{a}(s,s')+\gamma V_{i}(s')\right\},$

$여기$서 i$\displaystyle$i는$$ 반복 번호입니다.값 반복은 값 함수의 추측으로 i $=$ {$displaystyle$i$$=$}$ 및 V 0 {$displaystyle$ V_${0}$에서 시작합니다.그런 다음 V$${\$displaystyle$$$V$}$이(가) 오른쪽과 동일한 좌측과 수렴될 $때$까지 모든 $상태$의$$V${\displaystyle i_{}}$ +$$ {\$displaystyle V_{i+1}}$을(를) 반복적으로 $계산$합니다(이^{[clarification needed]} 문제에 대한 "벨만 방정식").확률적 게임에 대한 로이드 섀플리의 1953년 논문은 ^[6]민주당에 대한 가치 반복 방법을 특별한 사례로 포함시켰지만,^[7] 이것은 나중에야 인정되었다.

정책 반복

정책 반복(Howard 1960)에서는 스텝1이 1회 실행되고 다음으로 스텝2가 1회 실행되며 정책이 수렴될 때까지 양쪽이 반복됩니다.그런 다음 1단계를 다시 한 번 수행하고 계속 진행합니다.

수렴까지 2단계를 반복하는 대신 일련의 선형 방정식으로 공식화 및 해결할 수 있습니다.이러한 방정식은 2단계 ^{[clarification needed]}방정식의 s ${\displaystyle =}$ ${\displaystyle {}^{}}$ ${\$ \ $displaystyle$ s$=s'$로 $함$으로써 얻을 수 있습니다.따라서 2단계에서 수렴을 반복하는 것은 완화(반복법)로 선형 방정식을 푸는 것으로 해석할 수 있다.

이 변종에는 정지 조건이 정해져 있다는 장점이 있습니다$.즉, 순서1$을 모든 상태에 적용하는 동안 $어레이$가 변경되지$$ 않으면 알고리즘이 완료됩니다$.$

정책 반복은 일반적으로 많은 가능한 상태의 값 반복보다 느립니다.

수정된 정책 반복

변경된 정책 반복(van Nunen 1976; Puterman & Shin 1978)에서는 스텝1이 1회 실행되며 다음으로 스텝2가 여러 ^[8][9]번 반복됩니다.그런 다음 1단계를 다시 한 번 수행하고 계속 진행합니다.

우선 스위핑

이 변형에서는 알고리즘(최근에 V\$displaystyle$ V$\$$displaystyle V\pi}$에 큰 변화가 있었음) 또는 사용(이러한 상태는 시작 상태에 가깝음)에 관계없이 중요한 상태에 우선적으로 적용됩니다.(알고리즘을 사용한 프로그램)

확장 및 일반화

마르코프 결정 과정은 오직 한 명의 플레이어를 가진 확률 게임입니다.

부분 관측 가능성

위의 솔루션에서는 액션이 실행될 때 $s$가 이미 알려진 것으로 가정하고 있습니다.그렇지 않으면${\displaystyle }$($$) \$displaystyle \pi$ ( s$$)를 계산할 수 없습니다.이 가정이 사실이 아닌 경우, 이 문제는 부분적으로 관측 가능한 마르코프 결정 과정 또는 POMDP라고 불립니다.

이 분야에서 큰 진전이 "마르코프 의사결정 과정을 위한 최적의 적응 정책"^[10]에서 Burnetas와 Katehakis에 의해 제공되었다.이 연구에서, 총 예상 유한 수평 보상에 대해 균일하게 최대 수렴률 특성을 갖는 적응형 정책의 클래스는 유한 상태-작용 공간과 전환 법칙의 축소 불가능성의 가정 하에 구성되었다.이러한 정책은 각 주 및 기간에서의 조치 선택은 추정 평균 보상 최적성 방정식의 우측 팽창 지수에 기초해야 한다고 규정한다.

강화 학습

강화 학습은 확률이나 보상을 ^[11]알 수 없는 MDP를 사용한다.

이 목적을 위해 다음과 같은 추가 기능을 정의하는 $것$이 유용합니다$.$ 이 기능은 $액션$을 $실행$한 후 최적의 상태로 계속(또는 현재 보유하고 있는 정책에 따라)합니다.

$(\displaystyle \ Q(s,a)=\sum _{s'}P_{a}(s,s')(R_{a}(s,s')+\gamma V(s')).\ }$

이 기능도 알 수 없지만 학습 중 경험은 (${\displaystyle s}$ $displaystyle (s$, $a$)쌍$$${\displaystyle (}$$결과{\displaystyle {}^{}}$ s ${\$ { $displaystyle$ s$\text{'})$에 기초합니다. 즉, "$상태$에서 (\$displaystyle$$$s$')$를 $실행$하려고 했습니다$."$$따라서{\displaystyle }$ 어레이 Q$(\style$ Q$)$를 가지고 있으며 경험을 활용하여 직접 업데이트합니다.이를 Q-learning이라고 합니다.

강화 학습은 전환 확률을 명시적으로 지정하지 않고도 마르코프-결정 과정을 해결할 수 있다. 전환 확률의 값은 가치와 정책 반복에 필요하다.강화 학습에서, 전이 확률의 명시적인 지정 대신, 전이 확률은 일반적으로 균일하게 무작위적인 초기 상태에서 여러 번 다시 시작되는 시뮬레이터를 통해 액세스된다.강화 학습은 또한 함수 근사치와 결합하여 매우 많은 상태의 문제를 해결할 수 있다.

학습 오토마타

기계학습이론에서 MDP 프로세스의 또 다른 적용은 학습 오토마타라고 불린다.이것은 또한 환경이 확률적인 경우 강화 학습의 한 유형이다.첫 번째 상세 학습 오토마타는 원래 유한 상태 오토마타로 명시적으로 ^[12]기술된 Narendra와 Thathachar(1974)에 의해 조사되었다.강화 학습과 유사하게, 학습 자동 알고리즘은 확률이나 보상을 모를 때 문제를 해결할 수 있는 장점이 있습니다.학습 오토마타와 Q-러닝의 차이점은 이전 기법이 Q-값의 기억을 생략하지만 학습 결과를 찾기 위해 직접 행동 확률을 업데이트한다는 것이다.자동 학습은 ^[13]융합의 엄격한 증거를 가진 학습 체계이다.

자동 학습 이론에서 확률적 자동 학습은 다음과 같이 구성된다.

• 가능한 입력 x개,
• 가능한 내부 상태의 집합 δ = { δ₁, ..., δ_s },
• 가능한 출력 또는 작용의 집합 α = {α₁, ..., α }, r_r µs,
• 초기 상태 확률 벡터 p(0) = = = = = p₁ p(0), ..., p_s(0) ≫,
• 각 시간 단계 t 후에 p(t + 1)와 전류 입력 및 전류 상태로부터 p(t + 1)를 생성하는 계산 가능한 함수 A.
• 각 시간 단계에서 출력을 생성하는 함수 G: δ → α.

이러한 자동화의 상태는 "이산 상태 이산 매개 변수 마르코프 과정"^[14]의 상태에 해당한다.각 스텝 t = 0,1,2,3,…에서 오토마톤은 환경으로부터의 입력을 읽어내고, A에 의해 P(t)~P(t+1)를 갱신하고, 확률 P(t+1)에 따라 랜덤하게 후계 상태를 선택해, 대응하는 동작을 출력한다.오토마톤 환경은 동작을 읽고 다음 입력을 오토마톤에 ^[13]전송합니다.

범주 이론 해석

보상 이외에 마르코프 결정 과정$({\displaystyle S,}$ $)(\displaystyle(S, A, P))$은 범주 이론의 관점에서 이해할 수 있다.즉, A$(\$는 집합 A를 생성하는 유리 모노이드를 $나타낸다{\displaystyle \mathcal{}}$.Let Dist는 Giry 모나드의 Kleisli 범주를 나타냅니다.그런 다음 $펑터{\displaystyle \mathcal{}}$ ${\displaystyle A\mathbf{}}$ ${\displaystyle \to }$ ${\displaystyle \mathbf{Di}}$ s$$ \$displaystyle {\mathcal$ {$A}\$to \$mathbf${Dist$}}$는 상태 집합 S와 확률 함수 P를 모두 인코딩합니다.

이러한 방식으로 마르코프 결정 과정은 모노이드(하나의 객체가 있는 범주)에서 임의의 범주로 일반화될 수 있다.왜냐하면 한 개체에서 다른 C{\displaystyle{{C\mathcal}에서 움직이고 그 사람은 결과는 문맥에 마르코프 결정 과정{\displaystyle({\mathcal{C}},F:{\mathcal{C}}\to \mathbf{증류하다})}(C, F:C→ D나는 열심인 t),}}가능한 조치들 중 세트와 상태의 세트를 바꿔 부를 수 있습니다.[표창 필요한]

연속 시간 마르코프 결정 과정

이산 시간 마르코프 의사결정 프로세스에서 결정은 이산 시간 간격으로 이루어집니다.단, 연속시간 마르코프 결정 프로세스에 대해서는 의사결정자가 선택한 언제든지 결정을 내릴 수 있다.이산시간 마르코프 결정 프로세스와 비교하여 연속시간 마르코프 결정 프로세스는 연속역학을 갖는 시스템의 의사결정 프로세스를 더 잘 모델링할 수 있다. 즉, 시스템 역학은 편미분방정식(PDE)에 의해 정의된다.

정의.

연속 시간 마르코프 결정 프로세스를 논의하기 위해 두 가지 표기 세트를 도입한다.

상태 공간과 동작 공간이 유한하다면

• ${\displaystyle \mathcal{S}}${\$displaystyle\mathcal {S$ 상태 공간;
• $(\$ 액션 공간;
• ${\displaystyle q}$( i ${\displaystyle \mid j}$ ,${\displaystyle a}$) { $style q$ ( i \ $mid$j ,$a$) :${\displaystyle }S{\displaystyle \mathcal{}}$ × ${\displaystyle A\mathcal{}}$ →△$S$ { \ $displaystyle${ \$mathcal {$ S$$$}$ \ $times$ \ $rightarrow \ scal$ { A } , transition rate 함수 ;
• ${\displaystyle }$$R{\displaystyle \mathcal{}}$${\displaystyle }$(${\displaystyle i}$ , ${\displaystyle a}$) { $displaystyle$R ($i$ , $a$) :${\displaystyle }$S × ${\displaystyle A\mathcal{}}$ ${\displaystyle \to }$ { $style$\$mathcal { S$} \$times$ \ $tarrow$\ $mathbb${$R$ 보상 함수.

상태 공간과 작업 공간이 연속인 경우,

• $(\$ 상태 공간;
• $\$ 가능한 제어 공간;
• ${\displaystyle }$$f{\displaystyle \mathcal{}}$${\displaystyle }$(${\displaystyle x}$ ,${\displaystyle }$u$$) { $displaystyle$f ($x$ ,$u$ )$$:${\displaystyle X\mathcal{}}$( \ $displaystyle$ \ mathcal { X } \ $times$\ $mathcal${ $U }$\ $rightarrow \ transition$ rate 함수)
• ${\displaystyle }$$r{\displaystyle \mathcal{}}$ ${\displaystyle (x}$ ,${\displaystyle }$u$$) { $displaystyle$$$r ($x$ ,$u$${\displaystyle }$)$$:${\displaystyle }$X × ${\displaystyle U\mathcal{}}$ ${\displaystyle \to }$ { \ $displaystyle$\ $mathcal$ {$X }$ \$times$ \ $rightarrow$ \ $mathbb {$ R $\}$ ,${\displaystyle r}$( ${\displaystyle x}$ (${\displaystyle }$)${\displaystyle }$,$$ )${\displaystyle d}$ ${\displaystyle t=}$ ${\displaystyle R}$( $style$ )이전 사례에서 논의한 보상 기능.

문제

이산 시간 마르코프 의사결정 프로세스와 마찬가지로 연속 시간 마르코프 의사결정 프로세스에서 최적의 예상 통합 보상을 제공할 수 있는 최적의 정책 또는 제어를 찾고자 합니다.

$\displaystyle \max \operatorname {E} _{u} \left [ \ left ]\int _{0}^{\infty }\param ^{t}r(x(t),u(t)),dt\;\right x_{0}\right]}$

서 0 $.$ {\$display$ 0$\leq\display$< 1） 。$}$

선형 프로그래밍 공식

상태 공간과 동작 공간이 유한하다면 선형 프로그래밍을 사용하여 최적의 정책을 찾을 수 있습니다. 이는 가장 먼저 적용된 접근법 중 하나입니다.여기서는 에르고드 모델만 고려하는데, 이는 우리의 연속 시간 MDP가 정상 정책 하에서 에르고드 연속 시간 마르코프 체인이 된다는 것을 의미한다.이러한 가정 하에서 의사결정자는 현 상태에서는 언제든지 의사결정을 할 수 있지만 둘 이상의 조치를 취함으로써 더 많은 효익을 얻을 수 없다.시스템이 현재 상태에서 다른 상태로 이행할 때만 조치를 취하는 것이 좋습니다.일부 조건(상세한 내용은 연속 시간 마르코프 의사결정 프로세스의 결과 3.14 확인)에서 최적 가치 $함수{\displaystyle {}^{}}$ V ${\$ {\$display$ V$^{*}$이 $상태{\displaystyle }$i {\$displaystyle$ i$\}$와 독립적이라면 다음과 같은 부등식이 발생합니다.

$\displaystyle g\geq R(i,a)+\sum _{j\in S}q(j\mid i,a)h(j)\quad \forall i in S {\text {및 }}a(i)}$

$함수{\displaystyle }$ h$(\displaystyle$ h$)$가 존재할 $경우{\displaystyle {\stackrel{}{}}^{}}$ V$(\$는 위의 방정식을 충족하는$$ 최소 g$(\displaystyle$ g$)$가 됩니다.V ${\$ （ { $displaystyle$ { V$}$ }{*}}$$）를 찾으려면 다음과 같은 선형 프로그래밍 모델을 사용할 수 있습니다.

• 원시 선형 프로그램(P-LP)

${\displaystyle {begin {aligned} {\text {Minimize}} \ 쿼드 & g \ { \ text { s . t }}}\quad &g-\sum _{j\in S}q(j\mid i,a)h(j)\geq R(i,a),\forall i(in S,a)\end {aligned}}$

• 듀얼 리니어 프로그램(D-LP)

$({displaystyle {begin{aligned}{\text{Maximize}}&\sum_{i\in S}\sum_{a\in A(i)}R(i,a)y(i,a)\{\text{s.t}).}}&\sum _{i\in S}\sum _{a\in A(i)}q(j\mid i,a)y(i,a)=0\sum \forall j\in S,\sum _{i\in S}\sum _{a\in A(i)y\i,i\e(i)\i,i\i,i,i\sum \sum \sum$

${\displaystyle y}$${\displaystyle }$(${\displaystyle i}$ , ${\displaystyle a}$) $\$ $displaystyle$y ($i$ ,${\displaystyle a}$) \ $displaystyle$y ( i , a$$) \ displaystyle y ( i ,$a$ )가$$ 네이티브가 아니고 D-LP 문제의 제약 조건을 만족시키는 $경우{\displaystyle }$, y (${\displaystyle }$i , a )는 D-LP에 대한 실현 가능한 솔루션입니다.D-LP에 대한 실현 가능한 $솔루션{\displaystyle {}^{}}$ y${\displaystyle {}^{}}$ (${\displaystyle i}$ ,$$) ( \ $displaystyle$ y$^{*}(i,a)$ )는$$ 다음과 같은 경우 최적의 솔루션이라고 할 수 있다.

$({displaystyle {begin{aligned}\sum _{i\in S}\sum _{i,a)y^{*}(i,a)\geq \sum _{i\in A(i)}\sum _{a\in A(i)y(i,a)\end}} 정렬됨$

D-LP에 대한 모든 실현 가능한 $솔루션{\displaystyle }$ y${\displaystyle (i,}$ $)$ {$display y(i,a)}$에 대해 설명합니다.최적의 $솔루션{\displaystyle {}^{}}$ y ${\displaystyle {}^{}}$ ( ${\displaystyle i}$,${\displaystyle a}$ $){$ $displaystyle$ y$^{*}(i,a$를 찾으면 이를 사용하여 최적의 정책을 수립할 수 있습니다.

해밀턴-야코비-벨만 방정식

연속 시간 MDP에서 상태 공간과 작용 공간이 연속인 경우, 최적의 기준은 해밀턴-야코비-벨만(HJB) 편미분 방정식을 풀어서 찾을 수 있다.HJB 방정식을 논의하기 위해 우리는 우리의 문제를 재구성할 필요가 있다.

${\displaystyle {begin{aligned}V(x(0),0)={u}\int _{0}^{T}r(x(t),u(t)),dt+D[x(T)]\{\text{s.t}}}\frac {flac(t)}{dt}=f[t,x(t),u(t)]\end{aligned}}$

${\displaystyle D(\cdot )}$ is the terminal reward function, ${\displaystyle x(t)}$ is the system state vector, ${\displaystyle u(t)}$ is the system control vector we try to find. ${\displaystyle f(\cdot )}$ shows how the state vector changes over time.해밀턴-야코비-벨만 방정식은 다음과 같다.

$\displaystyle 0=\max _{u}(r(t,x,u)+{\frac {\flac V(t,x)}{\partial x}f(t,x,u)}}}f(t,x,u)}}}}$

우리는 최적의 값 함수 $V{\displaystyle {}^{}}$ ${\$ { \ $displaystyle$ V$^$ { * $\}$를 얻을 수 있는 최적의 $컨트롤{\displaystyle }$u (${\displaystyle t}$){ $displaystyle$u ($t$ )를 찾기 위해 방정식을 풀 수 있다.

어플

연속시간 마르코프 의사결정 프로세스는 큐잉 시스템, 전염성 프로세스 및 인구 프로세스에 응용된다.

대체 표기법

민주당에 대한 용어와 표기법은 완전히 정해지지 않았다.두가지 주요한 스트림 — 공학과 navigation[표창 필요한]에서 최소화 문제에게 다른 초점을 맞춘다 한 경제학 같은 맥락에서 극대화 문제에, 할인 요소 β 또는 γ에 전화하는 조건 액션, 보상, 값을 사용하여, 조건, 비용,cost-to-go을 통제하기를, 그리고 할인 요소 α 전화를 사용하여 초점을 맞추고 있다..또, 전이 확률의 표기법도 다릅니다.

이 기사에서	대안	댓글
행동 a	컨트롤 유
R에 보답하다	비용이 들다	g는 R의 음수이다.
값 V	가성비 J	J는 V의 음수이다.
정책 »	정책μ
할인 요인 »	할인인자α
$이행확률{\displaystyle {}_{}}$ ${\displaystyle P_{}}$ ${\displaystyle a{}_{}}$(${\displaystyle {}^{}}$ , s ${\displaystyle )}$ $){$ $displaystyle P_{a}$ (s$, s$ ) }	$이행확률{\displaystyle {}_{}}$ ${\displaystyle {{}^{}}_{}}$ ${\displaystyle {(}_{}}$ ( a${\displaystyle }$)$${ $displaystyle p_{ss'}$ ($a)$ }

또한 이행확률은 ${\displaystyle Pr}$( ${\displaystyle s}$,${\displaystyle {}^{}}$ , s ${\displaystyle )}$) { $displaystyle \Pr ( s$ ,$a$ , $s$)$$、 ${\displaystyle Pr}$( ${\displaystyle {}^{}ss}$ ,${\displaystyle }$a$$) 、 \ $displaystyle$$$\ $Pr$($$s ' \ $mid$s ,$$$a$ ) ${\displaystyle {{、}^{}}_{}}$, $p$ $s$ ( $a$)${\displaystyle }$。$}$

제한 마르코프 결정 과정

제약 마르코프 의사결정 프로세스(CMDP)는 마르코프 의사결정 프로세스(MDP)의 확장입니다.민주당과 CMDP 사이에는 ^[15]세 가지 근본적인 차이가 있다.

• 조치를 적용한 후 발생하는 비용은 한 가지가 아니라 여러 가지가 있다.
• CMDP는 선형 프로그램으로만 해결되며 동적 프로그래밍은 작동하지 않습니다.
• 최종 정책은 시작 상태에 따라 달라집니다.

CMDP 용 어플리케이션에는 여러 가지가 있습니다.최근 로봇 ^[16]공학에서 모션 플래닝 시나리오에 사용되고 있습니다.

「 」를 참조해 주세요.

레퍼런스

추가 정보

• Bellman., R. E. (2003) [1957]. Dynamic Programming (Dover paperback ed.). Princeton, NJ: Princeton University Press. ISBN 978-0-486-42809-3.
• Bertsekas, D. (1995). Dynamic Programming and Optimal Control. Vol. 2. MA: Athena.
• Derman, C. (1970). Finite state Markovian decision processes. Academic Press.
• Feinberg, E.A.; Shwartz, A., eds. (2002). Handbook of Markov Decision Processes. Boston, MA: Kluwer. ISBN 9781461508052.
• Guo, X.; Hernández-Lerma, O. (2009). Continuous-Time Markov Decision Processes. Stochastic Modelling and Applied Probability. Springer. ISBN 9783642025464.
• Meyn, S. P. (2007). Control Techniques for Complex Networks. Cambridge University Press. ISBN 978-0-521-88441-9. Archived from the original on 19 June 2010. 부록에 요약이 포함되어 있습니다.
• Puterman., M. L. (1994). Markov Decision Processes. Wiley.
• Ross, S. M. (1983). Introduction to stochastic dynamic programming (PDF). Academic press.
• Sutton, R. S.; Barto, A. G. (2017). Reinforcement Learning: An Introduction. Cambridge, MA: The MIT Press.
• Tijms., H.C. (2003). A First Course in Stochastic Models. Wiley. ISBN 9780470864289.

외부 링크

• Satinder P에 의한 마르코프 의사결정 과정 해결법 학습. 싱